Olá Habr!
Como
legisladores da
Unity no mercado russo, oferecemos a você um estudo interessante sobre o uso prático do algoritmo WFC (Wave Function Collapse), construído à imagem e semelhança do conhecido princípio da mecânica quântica e muito conveniente para a geração processual de níveis nos jogos. Anteriormente, em Habré, a
história detalhada sobre esse algoritmo já havia sido publicada. A autora do artigo de hoje, Marian Kleineberg, considera o algoritmo no contexto de gráficos tridimensionais e a geração de uma cidade sem fim. Boa leitura!
Falaremos sobre um jogo em que você percorre uma cidade sem fim gerada processualmente à medida que se move. Uma cidade é construída a partir de um conjunto de blocos usando o algoritmo WFC (colapso da função de onda).
A montagem reproduzível está disponível para download no site
itch.io. Você também pode pegar o
código fonte no github . Por fim, proponho um
vídeo no qual ando pela cidade assim gerada.
Algoritmo
Chamarei a palavra "célula" de um elemento de malha de voxel 3D que pode conter um bloco ou estar vazio. A palavra "módulo" chamarei um bloco que pode ocupar essa célula.
O algoritmo decide quais módulos selecionar em cada célula do mundo do jogo. Uma matriz de células é considerada uma função de onda em uma forma não observável. Assim, cada célula corresponde a muitos módulos que podem aparecer nela. Em termos de mecânica quântica, pode-se dizer: "a célula está em uma superposição de todos os módulos". A existência do mundo começa de uma forma completamente inobservável, onde qualquer módulo pode estar em cada célula. Além disso, todas as células entram em colapso, uma após a outra. Isso significa que, para cada célula, um módulo é selecionado aleatoriamente entre todos os possíveis.
O próximo passo é a propagação de restrições. Para cada módulo, é selecionado um subconjunto de módulos que podem ser adjacentes a ele. Cada vez que um módulo entra em colapso, subconjuntos de outros módulos são atualizados, que ainda são permitidos como adjacentes a ele. O estágio de propagação de restrições é a parte do algoritmo que consome mais recursos em termos de poder de computação.
Um aspecto importante do algoritmo é determinar qual célula recolher. O algoritmo sempre recolhe a célula com a
menor entropia . Essa é uma célula que permite um número mínimo de opções (ou seja, uma célula com o mínimo de aleatoriedade). Se a probabilidade de colapso for a mesma para todos os módulos, a célula com o número mínimo de módulos possíveis terá a menor entropia. Como regra, as probabilidades de serem selecionadas são diferentes para os vários módulos disponíveis. Uma célula com dois módulos possíveis com a mesma probabilidade fornece uma escolha mais ampla (maior entropia) do que aquela em que existem dois módulos, e para um deles a probabilidade de cair sob a escolha é muito alta e, para o outro, é muito pequena.

(Gif postado por
ExUtumno no Github)
Informações mais detalhadas sobre o algoritmo de colapso da função de onda, bem como vários exemplos bonitos, podem ser encontradas aqui. Inicialmente, este algoritmo foi proposto para gerar texturas 2D com base em uma única amostra. Nesse caso, os indicadores probabilísticos dos módulos e regras de adjacência são determinados dependendo da ocorrência no exemplo. Este artigo fornece essas informações manualmente.
Aqui está um
vídeo demonstrando esse algoritmo em ação.
Sobre blocos, protótipos e módulos
O mundo é gerado a partir de um conjunto em que cerca de 100 blocos. Eu os criei usando o Blender. No começo, eu tinha muito poucos blocos e os adicionei pouco a pouco quando considerou necessário.

O algoritmo precisa saber quais módulos podem ser localizados próximos um do outro. Para cada módulo, existem 6 listas de possíveis vizinhos, um em cada uma das direções. No entanto, eu queria evitar ter que criar essa lista manualmente. Além disso, eu queria gerar automaticamente opções giradas para cada um dos meus blocos.
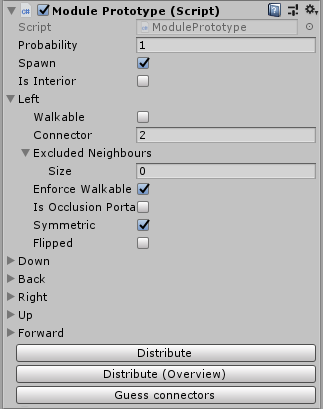
Ambas as tarefas são resolvidas usando os chamados módulos de protótipo. Em essência, esse é o
MonoBehaviour , que é conveniente trabalhar no editor do Unity. Módulos, juntamente com listas de elementos vizinhos válidos e opções rotadas, são criados automaticamente com base nesses protótipos.
Um problema complexo surgiu com a modelagem de informações de adjacência, para que esse processo automático funcionasse. Aqui está o que eu tenho:

Cada bloco possui 6 contatos, um para cada face. O contato tem um número. Além disso, os contatos horizontais podem ser invertidos, não invertidos ou simétricos. Os contatos verticais têm um índice de rotação no intervalo de 0 a 3 ou são marcados como
invariáveis rotativamente .
Com base nisso, posso verificar automaticamente quais módulos podem se encaixar. Os módulos adjacentes devem ter os mesmos números de pinos. Sua simetria também deve coincidir (o mesmo índice de rotação vertical, um par de contatos horizontais invertidos e não invertidos) ou os módulos devem ser simétricos / invariantes.
Existem regras de exclusão pelas quais posso proibir opções de bairro que seriam permitidas por padrão. Alguns blocos com contatos correspondentes simplesmente parecem feios nas proximidades. Aqui está um exemplo de um mapa gerado sem aplicar regras de exceção:

Caminho para o infinito
O algoritmo original de colapso da função de onda gera mapas de tamanho finito. Eu queria construir um mundo que se expandisse e se expandisse à medida que você se movesse.
No começo, tentei gerar fragmentos de tamanho finito e usar os contatos de fragmentos adjacentes como restrições. Se um fragmento é gerado, e um fragmento adjacente a ele também é gerado, somente esses módulos são permitidos que se ajustem ao lado dos módulos existentes. Com essa abordagem, surge o seguinte problema: sempre que uma célula entra em colapso, a propagação de restrições reduz as oportunidades, mesmo à distância de várias células. A imagem a seguir mostra os efeitos do recolhimento de uma única célula:

Se em cada etapa do algoritmo apenas um fragmento for gerado, as restrições não se aplicarão aos fragmentos adjacentes. Nesse caso, esses módulos foram selecionados dentro do fragmento que seriam inaceitáveis se outros fragmentos fossem levados em consideração. Como resultado, quando o algoritmo tentou gerar o próximo fragmento, não conseguiu encontrar uma única solução.
Agora não uso mais fragmentos, mas armazeno o mapa em um dicionário que exibe a posição de uma célula em uma célula. A célula é preenchida apenas se necessário. Alguns elementos do algoritmo devem ser ajustados com isso em mente. Ao escolher uma célula que deve entrar em colapso, é impossível levar em consideração todas as células se o número delas for infinito. Em vez disso, geramos apenas uma pequena parte do mapa de cada vez, quando o jogador o alcança. Fora desta área, as restrições continuam a se espalhar.
Em alguns casos, essa abordagem não funciona. Considere um conjunto de módulos para uma seção reta de um túnel da figura acima - não há entrada para o túnel. Se o algoritmo escolher um módulo de túnel, o túnel será infinito por definição. No estágio de distribuição de restrições, o programa tentará alocar um número infinito de células. Eu desenvolvi um conjunto especial de módulos para contornar esse problema.
Condições de contorno
Existem duas condições importantes de contorno. Todas as faces no nível superior do mapa devem ter contatos "aéreos". Todas as faces na base do mapa devem ter contatos "sólidos". Se essas condições não forem atendidas, no mapa haverá buracos no solo e alguns edifícios ficarão sem teto.
Em um mapa de tamanho finito, esse problema seria facilmente resolvido. Para todas as células nos níveis mais alto e mais baixo, seria necessário remover todos os módulos com contatos inadequados. Em seguida, inicie a distribuição de restrições e remova os módulos restantes que não são mais adequados para nós.
Em um mapa de tamanho infinito, isso não funcionará, porque, tanto no nível mais alto quanto no mais baixo, temos um número infinito de células. A solução mais ingênua é excluir todas as células inadequadas imediatamente à medida que elas surgirem. No entanto, quando um módulo é removido no nível superior, as restrições se aplicam às células adjacentes a ele. Há um efeito de avalanche, novamente levando a uma seleção infinita de células.
Resolvi esse problema criando um mapa 1 × n × 1, onde n é a altura. Este mapa usa quebra-cabeças para espalhar restrições. O mecanismo funciona como no jogo Pacman: indo além da borda direita do mapa, o personagem volta a ele por causa da borda esquerda. Agora posso aplicar quaisquer restrições ao meu mapa. Cada vez que você cria uma nova célula em um mapa infinito, essa célula é inicializada com um conjunto de módulos correspondentes a uma posição específica no mapa.
Condições de erro e pesquisa de retorno
Às vezes, o algoritmo WFC atinge um estado em que a célula não corresponde a nenhum módulo possível. Nas aplicações em que lidamos com um mundo de tamanho finito, você pode simplesmente redefinir o resultado e começar tudo de novo. Em um mundo infinito, isso não funcionará, pois parte do mundo já é mostrada ao jogador. Primeiro, decidi por uma solução em que os locais onde os erros ocorriam eram preenchidos com blocos brancos.
Atualmente, estou usando a pesquisa de retorno. A ordem do colapso das células e algumas informações sobre a distribuição de restrições são armazenadas na forma de histórico. Se o algoritmo WFC falhar, parte do histórico será cancelada. Como regra, isso funciona, mas às vezes os erros podem ser reconhecidos tarde demais, e uma pesquisa de retorno abrange muitas etapas. Em casos raros, a célula em que o jogador está localizado é regenerada.
Na minha opinião, devido a essa limitação, a aplicação do algoritmo WFC com mundos infinitos não é adequada para jogos comerciais.
Antecedentes
Comecei a trabalhar nessa tarefa depois de assistir a uma
palestra de Oscar Stelberg dizendo como ele usa o algoritmo para gerar níveis no jogo Bad North. Em geral, meu algoritmo foi implementado durante a semana do
procjam .
Tenho algumas idéias para aperfeiçoar ainda mais esse algoritmo, mas não tenho certeza de que algum dia adicionarei jogabilidade a ele. E se eu me reunir - com certeza não será uma estratégia tão épica que você já imaginou. No entanto, se você quiser verificar como sua mecânica de jogo favorita funciona com esse algoritmo - tente você mesmo! No final, o código fonte está disponível ao público e licenciado pelo MIT.