Geekly articles weekly

Talento vs. Sorte: O Papel da Chance no Sucesso e Fracasso



Recentemente, deparei-me com um trabalho interessante de cientistas italianos sobre o papel muito subestimado da sorte e do acaso em nossas vidas. Infelizmente, não encontrei a versão completa em russo (talvez estivesse parecendo mal?), Mas queria muito compartilhar o que li com meus colegas ingleses não fluentes. Portanto, arregaçando as mangas, ele começou sua tradução artesanal. Os autores, Alessandro, Alessio e Andrea, podem publicá-lo em domínio público; portanto, se você estiver interessado, seja bem-vindo ao gato.

Os autores


  • A. Pluchino - Departamento de Física e Astronomia, Universidade de Catania e Filial de Catania do Instituto Nacional de Física Nuclear, Itália; alessandro.pluchino@ct.infn.it
  • A. E. Biondo - Departamento de Economia e Negócios, Universidade de Catania, Itália; ae.biondo@unict.it
  • A. Rapisard - Departamento de Física e Astronomia, Universidade de Catania e Filial de Catania do Instituto Nacional de Física Nuclear, Itália; Centro de Estudos de Sistemas Complexos, Viena; andrea.rapisarda@ct.infn.it


Anotação


Em grande parte, as posições de liderança meritocrática dominante (a meritocracia é o princípio da administração, segundo a qual as pessoas mais capazes, independentemente de sua origem social e riqueza financeira ), lideram, o modelo altamente competitivo das culturas ocidentais se origina da crença de que o sucesso é principalmente, se não completamente, depende de qualidades pessoais como talento, inteligência, habilidades, desenvoltura, trabalho duro, perseverança, trabalho duro ou risco. Às vezes, estamos prontos para admitir que uma certa parte da sorte também pode desempenhar um papel na obtenção de sucesso material significativo. Mas, na verdade, a importância das forças externas nas histórias de sucesso individuais é frequentemente subestimada. É sabido que a inteligência (ou, geralmente, talento e qualidades pessoais) em uma população tem uma distribuição gaussiana, enquanto a distribuição de valores - geralmente vista como uma medida de sucesso - geralmente segue uma lei de poder (lei de Pareto) quando a maioria é pobre e existe um número insignificante de bilionários. Essa discrepância entre entradas normalmente distribuídas que têm um nível normal (talento ou inteligência médios) e uma distribuição constante na saída sugere que em algum lugar nos bastidores existe um componente invisível. Neste artigo, com base em uma simulação extremamente simples e baseada em agentes de brinquedos, assumimos que esse componente é um acidente comum. Em particular, mostramos que, embora o sucesso na vida realmente exija uma certa quantidade de talento, as pessoas mais talentosas quase nunca alcançam os mais altos picos de riqueza, sendo ultrapassadas por personalidades medíocres, mas muito mais bem-sucedidas. Até onde sabemos, esse resultado contraditório do senso comum - embora implicitamente assumido nas entrelinhas de muita literatura - foi o primeiro a fazer uma avaliação quantitativa. Isso permite que você revise a eficácia da avaliação dos méritos com base no nível de sucesso já alcançado e enfatiza os riscos de distribuir honras ou recursos excessivos a pessoas que, a longo prazo, podem ser mais bem-sucedidas do que outras. Utilizando esse modelo, também consideramos e comparamos várias hipóteses comportamentais para mostrar as estratégias mais eficazes de financiamento público à pesquisa, com o objetivo de melhorar a meritocracia, a diversidade e a inovação.

1. Introdução


A onipresença da dependência da lei do poder em muitos sistemas complexos físicos, biológicos ou socioeconômicos pode ser considerada como uma característica matemática distinta da estreita relação de suas características dinâmicas com uma estrutura topológica inalterada em escala [1, 2, 3, 4]. No contexto socioeconômico, de acordo com o trabalho de Pareto [5, 6, 7, 8, 9], é sabido que a distribuição da riqueza tem um caráter de lei do poder, cuja forma alongada característica reflete a profundidade do abismo existente entre os ricos e os pobres de nossa sociedade.

Um relatório recente [10] mostra que hoje essa lacuna é muito maior do que temíamos: oito pessoas possuem a mesma riqueza que 3,6 bilhões de pessoas, que constituem a parte mais pobre da humanidade. Nos últimos 20 anos, vários modelos teóricos foram desenvolvidos para calcular a distribuição de valores no contexto da teoria das probabilidades e estatística física, muitas vezes assumindo a forma de modelagem multiagente com dinâmica interna simples [11, 12, 13, 14, 15, 16, 17].

Indo mais longe nessa direção, se considerarmos a riqueza pessoal como uma medida de sucesso, pode-se argumentar que sua distribuição profundamente assimétrica e desigual entre as pessoas é uma consequência de suas diferenças naturais em talento, habilidades, competência, inteligência, habilidades ou na medida de sua perseverança, trabalho duro ou intencionalidade. Tal suposição, de forma implícita, é a base do chamado paradigma meritocrático: afeta não apenas como nossa sociedade oferece oportunidades de emprego, honra e fama, mas também as estratégias adotadas pelos governos para alocar recursos e financiamento àqueles que são considerados os mais personalidades honradas.

No entanto, a conclusão anterior parece ser muito diferente dos dados confirmados de que as propriedades e qualidades das pessoas acima mencionadas são normalmente distribuídas por toda a população, ou seja, correspondem a uma distribuição gaussiana simétrica em relação a essa média. Por exemplo, a inteligência, medida pelos testes de QI, corresponde ao seguinte padrão: o QI médio é 100, mas ninguém tem um QI de 1000 ou 10000. O mesmo se aplica ao trabalho contado em horas de trabalho: alguém trabalha mais que a média, outro menos, mas não há ninguém que trabalhe um bilhão de vezes mais horas que o resto.

Porém, em nosso tempo, há cada vez mais evidências sobre o papel fundamental do acaso, da sorte ou, em geral, de fatores aleatórios, na determinação do sucesso ou fracasso em nossos assuntos pessoais e profissionais. Em particular, foi demonstrado que todos os cientistas têm a mesma chance de publicar trabalhos inovadores durante suas carreiras [18]; que aqueles com a primeira letra do nome de família mais próxima do início do alfabeto têm muito mais chances de receber o cargo de chefe de departamento [19]; que as distribuições dos indicadores bibliométricos coletados pelos cientistas podem se tornar aleatórias e sem sentido devido ao crescente fenômeno associado ao mecanismo inflacionário “publicar ou morrer” [20]; que a posição de alguém em uma lista classificada alfabeticamente pode ser importante para determinar o acesso a serviços públicos limitado pelo número de lugares [21]; que a letra inicial do nome do meio levanta uma avaliação das habilidades intelectuais [22]; que pessoas com nomes de pronúncia fácil são classificadas de maneira mais positiva do que aquelas cujos nomes são complexos [23]; que aqueles cujos nomes soam mais aristocráticos com mais freqüência do que outros trabalham como líderes e não subordinados [24]; que mulheres com apelidos masculinos são mais bem-sucedidas na profissão legal [25]; que aproximadamente metade das diferenças de renda entre as pessoas em todo o mundo é explicada apenas pelo país de residência e pela distribuição de salários no respectivo país [26]; que a probabilidade de se tornar diretor é grandemente influenciada por seu nome e mês de nascimento [27, 28, 29]; que idéias inovadoras são o resultado de reações aleatórias nas células do nosso cérebro [30]; e que mesmo a probabilidade de desenvolver câncer, possivelmente destruindo uma excelente carreira, depende em grande parte do fracasso [31, 32]. Trabalhos recentes sobre o tema do sucesso reprodutivo ao longo da vida contribuem para a confirmação de tais afirmações, mostrando que se os desvios de características podem afetar o destino da população como um todo, então a vida de indivíduos específicos é frequentemente determinada pela sorte.

Nos últimos anos, muitos autores, incluindo o estatístico e analista de risco Nassim Taleb [35, 36], o estrategista de investimentos Michael Mobussin [37] e o economista Robert Frank [38], investigaram em vários livros populares a conexão entre sorte e habilidade em transações financeiras. negócios, esportes, arte, música, literatura, ciência e muitas outras áreas. Eles concluíram que eventos aleatórios desempenham um papel muito maior na vida do que muitos teriam imaginado. De fato, eles não assumem que o sucesso não dependa de talentos e esforços, pois em áreas ou mercados extremamente competitivos, como “o vencedor leva tudo”, onde vivemos e trabalhamos atualmente, as pessoas mais produtivas são quase sempre extraordinárias talentoso e trabalhador. Eles concluíram apenas que talento e esforço não são suficientes: você também precisa estar no lugar certo, na hora certa. Em suma, a sorte também afeta, embora seu papel seja quase sempre subestimado pelas pessoas de sucesso. Isso se deve ao fato de que a aleatoriedade geralmente funciona de maneira não óbvia; portanto, é fácil comparar eventos que mostram sucesso como algo inevitável. Taleb chama essa inclinação de "uma falácia fantástica" [36], e o sociólogo Paul Lazarsfeld propôs o termo "retrospectiva tendenciosa". Em seu livro mais recente, "Tudo é óbvio: quando você sabe a resposta" [39], o sociólogo e pioneiro da ciência de redes Duncan Watts sugere que tanto a ilusão fabulosa quanto a retrospectiva tendenciosa apelam a um fenômeno especial no qual pessoas que veem resultados extraordinariamente bem-sucedidos considerá-los como um produto indubitável de trabalho duro e talento. No entanto, o sucesso surge principalmente através de etapas complexas e entrelaçadas, cada uma das quais depende das anteriores: se alguma delas fosse diferente, toda a carreira ou trajetória de vida quase certamente também seria diferente. Esse argumento também se baseia nos resultados de um estudo experimental inovador realizado vários anos antes pelo próprio Watts, em colaboração com outros autores [40], no qual o sucesso de músicas anteriormente desconhecidas no mercado de música artificial não demonstrou correlação com a qualidade do trabalho em si. E isso, é claro, complica muito qualquer previsão, como mostrado em outro estudo mais recente [41].

Neste artigo, usando uma abordagem estatística baseada em agentes, tentaremos determinar quantitativamente praticamente o papel da sorte e do talento em carreiras de sucesso. Na Seção 2, com base no número mínimo de premissas, a saber, a natureza gaussiana da distribuição de talentos [42] e a dinâmica multiplicativa de sucessos e fracassos [43], apresentamos um modelo simples, que chamamos de modelo "Talento vs. Sorte" (TPU), em que imita o desenvolvimento de carreiras profissionais de um grupo de pessoas ao longo dos 40 anos de trabalho. O modelo mostra que, na realidade, a aleatoriedade desempenha um papel fundamental na determinação dos indivíduos mais bem-sucedidos. O certo é que, como se poderia esperar, é mais provável que pessoas talentosas se tornem ricas, famosas ou significativas em suas próprias vidas, em relação às menos preparadas. Mas, e essa explicação menos intuitiva, pessoas comuns com um nível comum de talento estão estatisticamente destinadas a se tornarem bem-sucedidas (ou seja, localizadas no final de uma distribuição de poder de sucesso) com muito mais frequência do que as mais talentosas, desde que se tornem favoritas da sorte da sua vida. Esse fato é frequentemente encontrado, como indicado nas referências [35, 36, 38], mas, tanto quanto sabemos, foi modelado e medido pela primeira vez neste trabalho.

O sucesso de pessoas com talento comum questiona o paradigma "meritocrático" e todas as estratégias e mecanismos que deram mais recompensas, oportunidades, honra, fama e recursos às pessoas consideradas as melhores em seu campo [44, 45]. O fato é que, na grande maioria dos casos, todas as avaliações do talento de alguém foram feitas após o fato, apenas observando sua atividade ou os resultados alcançados em uma área específica da nossa sociedade, como esportes, negócios, finanças, arte , ciência etc. Esse tipo de avaliação enganosa leva a uma substituição de causa e efeito, avaliando como as pessoas mais talentosas aquelas que são, simplesmente, as mais bem-sucedidas [46, 47]. De acordo com essa visão, trabalhos anteriores alertaram para tipos semelhantes de “quase meritocracia” e mostraram a eficácia de outras estratégias baseadas em amostras aleatórias em muitos ambientes diferentes, como gerenciamento, política e finanças [48, 49, 50, 51, 52, 53, 54, 55]. Na Seção 3, aplicamos nossa abordagem e descrevemos como a distribuição de fundos públicos é possível no contexto da pesquisa científica. Estudamos as consequências de várias estratégias de distribuição, dentre as quais há uma meritocrática "quase", com o objetivo de explorar novas maneiras de aumentar, ao mesmo tempo, o nível mínimo de sucesso das pessoas mais talentosas da sociedade e a eficácia total dos gastos do governo. Examinaremos também, em geral, como as oportunidades oferecidas pelo meio ambiente, apresentadas na forma de níveis de educação e renda (ou seja, fatores externos, dependendo do país e da camada social de onde as pessoas provêm), são importantes para aumentar a probabilidade de sucesso. As considerações finais completam o trabalho.

2. Modelo


Além disso, propomos um modelo de agente chamado "Talent versus Good Luck" (TPU), com base em um pequeno número de suposições, com o objetivo de descrever a evolução das carreiras de um grupo de pessoas sob a influência de eventos aleatórios e bem-sucedidos.


Figura 1: Um exemplo dos parâmetros iniciais para a nossa simulação. Todas as simulações apresentadas neste artigo foram realizadas no ambiente de simulação do agente NetLogo [56]. N = 1000 pessoas (agentes), com graus variados de talento (inteligência, habilidades, etc.) distribuídos aleatoriamente em posições fixas no mundo quadrado de seções 201 × 201 com condições de contorno cíclicas. Durante cada simulação, que se estende por várias décadas, eles são expostos a um certo número de eventos bem sucedidos (círculos verdes) e mal sucedidos (círculos vermelhos) que se movem pelo mundo ao longo de trajetórias aleatórias (caminhada aleatória). Neste exemplo, N E = 500.

Consideramos N indivíduos com talento T (intelecto, habilidades, habilidades, etc.) tendo uma distribuição normal no intervalo [0; 1] em torno de uma dada média m T com um desvio padrão σ T aleatoriamente colocado em posições fixas dentro do mundo quadrado (veja a Figura 1) com condições de contorno cíclico (isto é, com uma topologia toroidal) e cercado por um certo número N E de “movimento” eventos (marcados com pontos), alguns dos quais são bem-sucedidos, nenhum outro (eventos neutros neste modelo não são levados em consideração, pois não têm consequências significativas na vida do indivíduo). Na Figura 1, mostramos esses eventos na forma de pontos coloridos: bem-sucedidos em verde e com uma porcentagem relativa de p L , e malsucedidos em vermelho e com uma porcentagem ( 100 - p L ). O número total de pontos de evento N E é distribuído uniformemente, mas, é claro, essa distribuição será idealmente uniforme apenas para N E → ∞ . Em nossas simulações, normalmente haverá N E ≈ N / 2 ; portanto, no início de cada simulação, há uma concentração significativa aleatória de pontos de evento com ou sem êxito em várias regiões do mundo, enquanto outras regiões serão mais neutras. O movimento aleatório subsequente de pontos dentro de uma matriz quadrada, ou seja, o mundo, não altera esse recurso fundamental do modelo, que indica um número diferente de eventos de sucesso ou fracasso para diferentes pessoas ao longo de suas vidas, não dependendo de seu talento pessoal.


Figura 2: distribuição normal de talento entre a população (com a mediana m T = 0,6 mostrada por uma linha vertical tracejada e o desvio padrão σ T = 0,1 - os valores m T ± σ T são exibidos como duas linhas verticais pontilhadas). Essa distribuição é alocada no intervalo [0; 1] e não muda durante a simulação.

Uma execução de simulação examina um período de vida útil P de 40 anos (vinte a sessenta anos), com um intervalo de tempo δ t de seis meses. No início da simulação, todos os agentes receberam o mesmo capital C i = C (0) Ɐ i = 1, ..., N , representando seu nível inicial de sucesso / bem-estar. Essa escolha tem o objetivo óbvio de não dar a ninguém a vantagem inicial. Enquanto o talento dos agentes não depende do tempo, seu capital está mudando. Durante o desenvolvimento desse modelo, ou seja, durante o período esperado da vida dos agentes, todos os pontos de eventos se movem aleatoriamente ao redor do mundo e, ao mesmo tempo, podem se cruzar com a localização de alguns agentes. Se você entrar em detalhes, cada vez que cada ponto do evento cobre, em uma direção aleatória, a distância de 2 seções. Acreditamos que existe uma interseção com o indivíduo se o ponto do evento representado dentro do círculo com um raio de um segmento estiver centrado no agente (os pontos do evento não desaparecem após a interseção).Dependendo desse incidente, nesta etapa t (ou seja, a cada seis meses), com um determinado agente A k , são possíveis as três opções possíveis a seguir:

  1. Nenhum ponto de evento cruza a posição do agente A k - isso significa que durante os últimos seis meses nenhum evento ocorreu, o agente A k não executa nenhuma ação.
  2. A k – , ( , [30], , ); , A k / , T k . C k (t) = 2C k (t − 1) , rand[0; 1] < T k , .., , .
  3. A k – , ; , A k / , .. C k (t) = C k (t − 1) / 2 .


( , ), , , , . , , , ( , ). , , , , . , «», « , ». , «» , , , , , , , , . , , .

2.1


. , , , , , .

N = 1000 C (0) = 10 ( ) T i ϵ [0; 1], m T = 0,6 σ T = 0,1 (. 2). , P = 40 , , , I = 80 . N E = 500 , p L = 50%.

, () 3, , / , () (). , (b) , y© ≈ C −1,27 .

, , , , , : . , 4 500 , 20 44% , 10 . , «80/20», 80% 20% , 20% 80% . , , , , , / , . ?


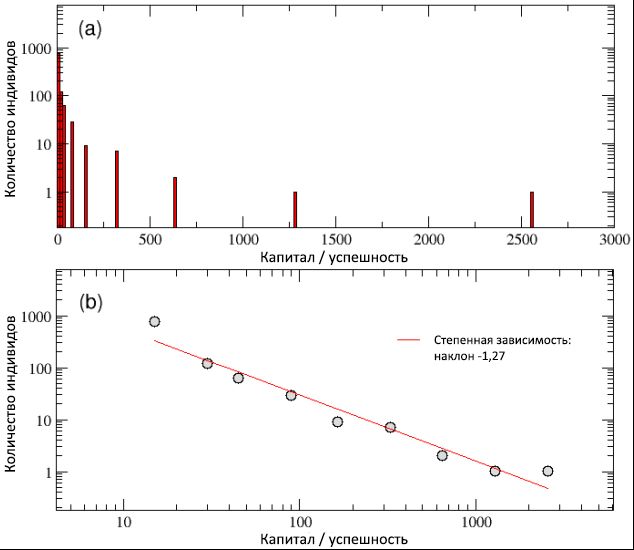Figura 3: A distribuição final da riqueza / sucesso entre a população, em uma escala linear logarítmica (a) e bilogarítmica (b). Apesar da distribuição normal de talentos, o final da distribuição de sucesso, como pode ser visto no esquema (b), pode ser descrito como uma curva de potência com uma inclinação de -1,27. Também confirmamos que a distribuição de capital / sucesso segue a lei 80/20 de Pareto, já que 20% da população possui 80% dos valores e vice-versa.

4, (a) (b), , / , ( , (a) / – ). , , , , , . , , C max = 2560, T* = 0,61, m T = 0,6, ( T max= 0,89) possui uma taxa de capital / sucesso inferior a 1 unidade ( C = 0,625).

Conforme aprendemos com mais detalhes na próxima subseção, esse resultado não é um caso especial, mas uma regra para sistemas desse tipo: o sucesso máximo nunca coincide com o talento máximo e vice-versa. Além disso, essa discrepância entre sucesso e talento é desproporcional e altamente não linear. De fato, o capital médio de todas as pessoas com talento T> T * é C ≈ 20; , / 128 , / , , . , , , , . , .


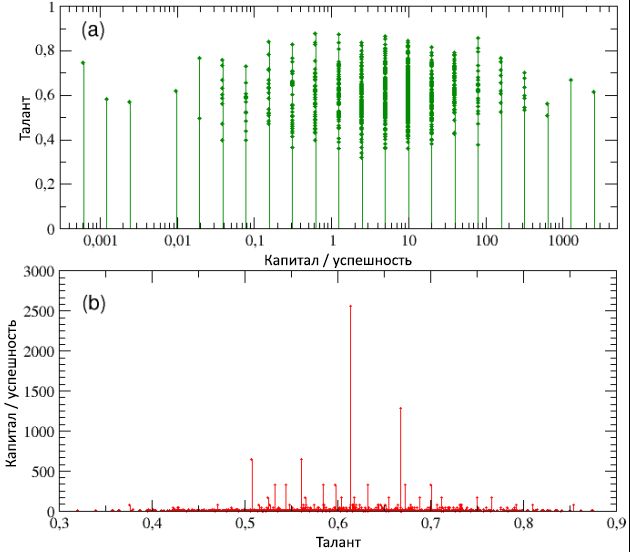
4: () / ( , ) – , , , . (b), , / – , , C max = 2560, , m T = 0,6, / , C = 1 , C (0). .

5 , , / . (a) , ( , , , , , ). , (b), , . , , , , . , , © (d), , 0,64 0,48, 1,35 1,66, , , , 10 15. , 16% «» , , 40% - ( ).

/ , , , 40 (80 , 6 ) . , , 6. (a) 5, , , , .


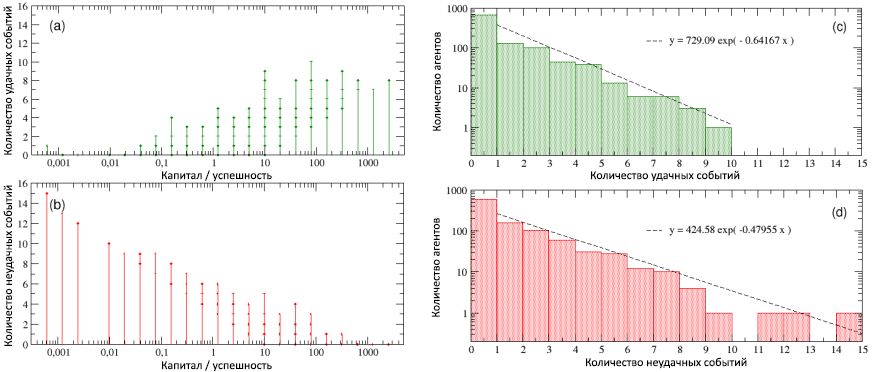Figura 5: número total de eventos bem-sucedidos (a) e malsucedidos (b), em função do sucesso do capital / agente. O gráfico mostra uma forte correlação entre sucesso e sucesso: os indivíduos mais bem-sucedidos também são os mais bem-sucedidos e vice-versa. Novamente, devido ao uso do mesmo capital inicial para todos os agentes, verifica-se que vários eventos são agrupados em valores discretos de capital / sucesso. Nos diagramas © e (d), a frequência das distribuições, respectivamente, do número de eventos com e sem êxito é exibida em uma escala log-linear. Como pode ser visto, ambas as distribuições podem ser escritas na forma de dependências exponenciais com poderes negativos semelhantes).

( ) (a) 6, , , , , ( ), ( ), , 30 40 (.. 40- ) , 10 (.., 5 ) , C = 320 C max = 2560.

, ( ) (b) , , , , , / , C = 0,00061. , T = 0,74, , . , . , , ( ), , , , .


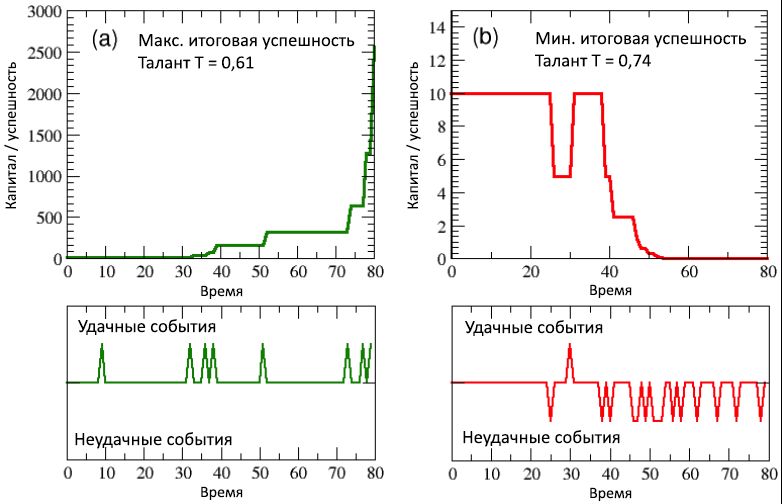
6: (a) / (b) , , ( 80 , .., 40 ). , .

(- NetLogo , , Open ABM), , , , , , , , .

2.2


Nesta subseção, apresentamos os resultados da simulação geral de, em média, mais de 100 execuções, cada uma iniciada com diferentes condições iniciais selecionadas aleatoriamente. Os valores dos parâmetros de controle foram os mesmos da subseção anterior: N = 1000 indivíduos, m T = 0,6 e σ T = 0,1 para a distribuição normal de talento, I = 80 iterações (cada um representa δ t = 6 meses de vida profissional ), C (0) = 10 unidades de capital inicial, E = 500 pontos de evento e a porcentagem de eventos bem-sucedidos p L = 50%.

No diagrama (a) da Figura 7, a distribuição total do capital / sucesso total entre todos os agentes coletados como resultado de 100 execuções é mostrada em uma escala logarítmica e é bem descrita por uma curva de potência com um coeficiente angular de -1,33. A propriedade de capital constante observada em uma única execução, independentemente da escala e a alta desigualdade resultante entre os indivíduos, bem como a regra Pareto “80/20”, foram preservadas no caso de múltiplas execuções. De fato, a diferença entre os agentes ricos (bem-sucedidos) e os pobres (mal-sucedidos) aumentou ainda mais, já que a capital das pessoas mais ricas já ultrapassou 40.000 unidades.

É possível estimar melhor esse resultado observando o esquema (b) da Figura 7, em que o capital total Cmax apenas dos indivíduos mais bem-sucedidos é mostrado em função do talento mostrando o melhor resultado em cada uma das 100 execuções. O agente com o talento T melhor = 0,6048, quase coincidindo com a mediana da distribuição de talentos ( m T = 0,6), que atingiu o pico de capital C melhor = 40960, recebeu mais pontos, por outro lado, o mais talentoso dos indivíduos mais bem-sucedidos, com talento T max = 0,91, ganhou capital C max = 2560, o que representa apenas 6% da C melhor .


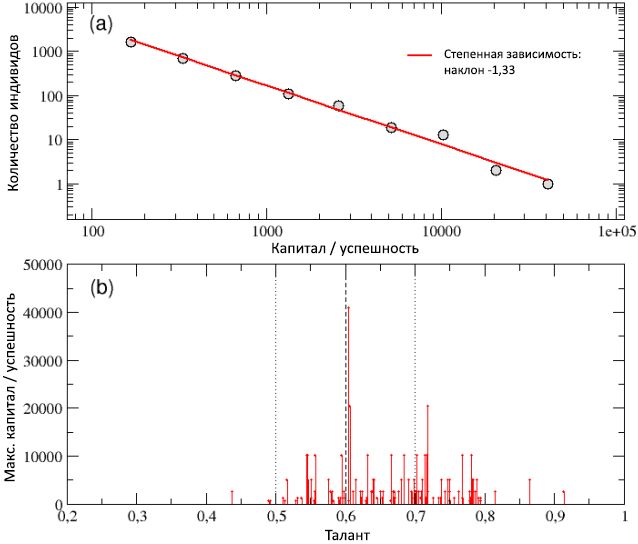
Figura 7: Esquema (a) - distribuição do capital total / sucesso calculado em 100 execuções para populações com diferentes condições iniciais determinadas aleatoriamente. A distribuição pode ser descrita por uma curva de potência com uma inclinação de -1,33. Esquema (b) - o capital total Cmax dos indivíduos mais bem-sucedidos em cada uma das 100 execuções, mostrado em função de seu talento. Pessoas com talento moderadamente alto, em média, são mais bem-sucedidas do que aquelas que têm talento baixo ou moderado e, na maioria das vezes, o indivíduo mais bem-sucedido é um agente moderadamente talentoso, e apenas ocasionalmente o mais talentoso. O valor de m T , bem como os valores de m T ± σ T , são mostrados, respectivamente, na forma de linhas tracejadas e pontilhadas verticais.

Para considerar esse ponto de vista com mais detalhes, na Figura 8 (a), plotamos a distribuição de talentos dos melhores desempenhos, calculada para 100 execuções. A distribuição, obviamente, é deslocada para a direita ao longo do eixo do talento, com um valor médio de T av = 0,66> m T - isso confirma, por um lado, que para alcançar um sucesso significativo, muitas vezes é necessário um talento moderadamente alto; no entanto, por outro lado, também mostra que essa condição quase nunca é suficiente, uma vez que os agentes com o maior talento (ou seja, com T > m T = 2σ T ou T > 0,8) estão entre os melhores desempenhos em 3% dos casos, e seu capital / sucesso nunca excede 13% da C melhor .


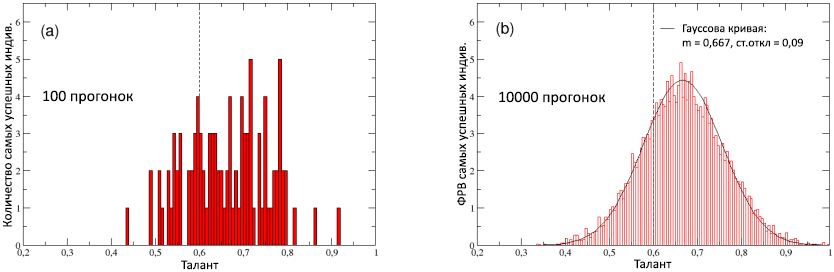
Figura 8: (a) Distribuição de talentos das personalidades mais bem-sucedidas (melhores desempenhos) em cada uma das 100 execuções. (b) A função de distribuição de probabilidade (RFF) do talento dos indivíduos mais bem-sucedidos, calculada em 10.000 execuções: é bem descrita pela distribuição normal com uma mediana de 0,667 e um desvio padrão de 0,09 (curva sólida). Para comparação, é mostrada a mediana m T = 0,6 da distribuição normal inicial de talentos na população, mostrada nos dois esquemas por uma linha vertical tracejada.

No diagrama (b) da Figura 8, a mesma distribuição (reduzida à área total para obter a FRF) é calculada para 10.000 execuções para entender sua verdadeira forma: parece que ela se encaixa na curva Gaussiana G (T) com a média T av = 0,667 e um desvio padrão de 0,09 (linha sólida). Obviamente, isso confirma que a distribuição de talentos dos melhores desempenhos é deslocada para a direita em relação ao eixo do talento, em comparação com a distribuição inicial. Para ser mais preciso, isso significa que a probabilidade condicional P ( C max | T ) = G (T) dT de encontrar entre os melhores desempenhos uma personalidade com talento no intervalo [ T ; T + dT ] cresce com o talento T , atinge um pico próximo ao talento médio-moderado T av = 0,66 e depois cai acentuadamente com grandes valores de talento. Em outras palavras, a probabilidade de encontrar um indivíduo moderadamente talentoso além do sucesso é maior do que encontrar um indivíduo altamente talentoso lá. Observe que em um mundo ideal em que o talento foi a principal razão do sucesso, espera-se que P ( C max | T ) seja uma função crescente de T. Assim, podemos concluir que a forma gaussiana observada P ( C max | T ) é uma evidência de uma importância maior da sorte do que o talento para alcançar níveis extremamente altos de sucesso.


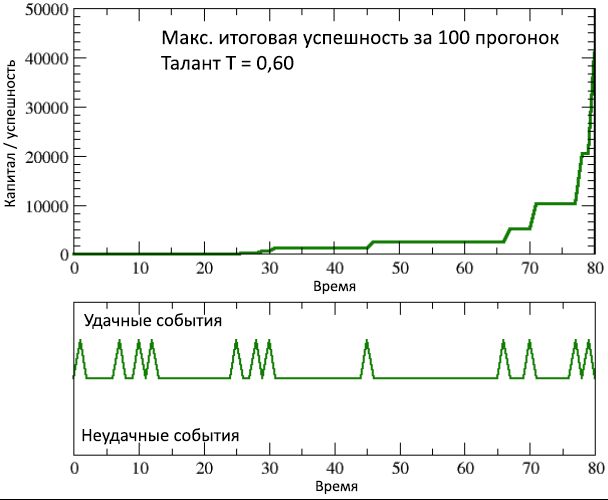
Figura 9: mudança no tempo de sucesso / capital da pessoa mais bem-sucedida (mas ao mesmo tempo, moderadamente talentosa), de 100 execuções de simulação, em comparação com a sequência incomum correspondente de eventos de sucesso que aconteceram em sua vida.

Também é interessante comparar, a partir de 100 execuções, a taxa média de capital / sucesso C mt ≈ 63 das pessoas mais talentosas com a correspondente C média em ≈ 33 daqueles cujo talento está próximo da mediana m T. Em ambos os casos, encontramos indicadores bastante baixos (mesmo que mais do que o capital inicial C (0) = 10), mas o fato de C mt > C at indica que, embora a probabilidade de encontrar um indivíduo moderadamente talentoso no topo do sucesso seja maior, do que aquele que é altamente talentoso, os indivíduos mais talentosos de cada corrida são, em média, mais bem-sucedidos do que as pessoas moderadamente talentosas. Por outro lado, observando a média acima de 100 execuções, a proporção de indivíduos com talento T > 0,7 (ou seja, maior que com um desvio padrão da mediana) e o sucesso final / capital C final > 10, calculados considerando todos os agentes com talento T > 0,7 (dos quais, em média, para cada corrida, ≈ 160), descobrimos que essa participação é de 32% - isso significa que o desempenho combinado das pessoas mais talentosas da nossa população é, em média, relativamente pequeno, pois apenas um terço deles atinge um capital total que excede o original.

De qualquer forma, o melhor desempenho entre as 100 simulações é um agente com o talento T best = 0,6, que combina perfeitamente com a mediana e com o sucesso final C best = 40960, que é 650 vezes mais que o C mt , é irrefutável . e mais de 4.000 vezes superior ao sucesso de C <<10 em 2/3 das pessoas mais talentosas. Isso aconteceu, no final, simplesmente porque ele teve mais sorte do que o resto. Sorte incondicional, como pode ser visto na Figura 9, que mostra o crescimento de seu capital / sucesso ao longo de sua vida profissional, juntamente com uma impressionante série de eventos bem-sucedidos (e apenas bem-sucedidos), dos quais, apesar da falta de talento excepcional, ele conseguiu lucrar durante seus carreiras.

Resumindo, neste ponto, verificou-se que, apesar de sua simplicidade, o modelo TPU parece ser capaz de levar em consideração muitas características que caracterizam, como mencionado na introdução, a alta desigualdade na distribuição de riqueza e sucesso em nossa sociedade, o que contrasta claramente com a distribuição gaussiana de talento entre os pessoas. Além disso, o modelo em forma quantitativa mostra que um grande talento não é suficiente para uma carreira de sucesso garantida e que, pelo contrário, pessoas menos talentosas muitas vezes atingem o auge do sucesso - esse é outro "fato condicional" geralmente observado na vida real [35, 36, 38].

Um aspecto fundamental que explica intuitivamente como pode acontecer que indivíduos moderadamente talentosos obtenham (com tanta freqüência) muito mais honra e sucesso, em comparação com indivíduos mais talentosos, é que existe um papel oculto e muitas vezes subestimado da sorte, como é claramente visto de nossas simulações. Mas, para entender o verdadeiro significado dos resultados de nossa pesquisa, é importante distinguir entre o ponto de vista macro e o micro.

De fato, no nível micro, seguindo as regras dinâmicas do modelo TPU, um indivíduo talentoso tem, a priori, maior probabilidade de alcançar um alto nível de sucesso do que um moderadamente talentoso, pois possui maior capacidade de aproveitar a oportunidade. Assim, do ponto de vista de um indivíduo, devemos concluir que, não sendo possível (por definição) influenciar a aparência de eventos de sucesso, a melhor estratégia para aumentar a probabilidade de sucesso (em qualquer nível de talento) é expandir a atividade pessoal, gerar idéias, comunicar com outras pessoas, a busca da diversidade e do enriquecimento mútuo. Em outras palavras, tornar-se uma pessoa de mente aberta que está pronta para entrar em contato com outras pessoas oferece a maior probabilidade de um evento bem-sucedido (que será realizado com o melhor talento da personalidade).

Por outro lado, no nível macro, do ponto de vista de toda a sociedade, a probabilidade de encontrar pessoas moderadamente talentosas no topo do sucesso é muito maior do que encontrar pessoas extremamente talentosas lá, porque as primeiras são muito maiores e, graças à sorte, elas têm, em geral, a vantagem de alcançar um tremendo sucesso, apesar da menor probabilidade pessoal a priori.

Na próxima seção, consideraremos esse ponto de vista em nível macro, explorando as oportunidades oferecidas por nosso modelo para estudar mais detalhadamente estratégias e políticas mais eficazes para melhorar o nível médio de desempenho das pessoas mais talentosas da população, implementando formas mais produtivas de distribuir recompensas e recursos. De fato, esperamos que qualquer política que possa aumentar o nível das pessoas mais talentosas que são o motor do progresso e da inovação em nossa sociedade tenha um efeito benéfico cumulativo.

3. Estratégias eficazes de equilíbrio da sorte


Os resultados apresentados na seção anterior são claramente consistentes com as evidências empíricas documentadas na introdução, que põem em causa a suposição meritocrática de que as diferenças naturais de talento, habilidades, habilidades, inteligência, trabalho duro ou perseverança são as únicas razões para o sucesso. Como mostramos, a sorte também tem um impacto e pode desempenhar um papel crucial. A essência da discussão é que, devido à difícil mensurabilidade (em muitos casos, é difícil determinar em termos exatos) das qualidades pessoais, as estratégias meritocráticas são frequentemente usadas para distribuir honras, financiamentos ou prêmios, geralmente baseados em resultados privados, medidos em termos de riqueza ou sucesso pessoal. Como resultado, essas estratégias influenciam as ações adicionais para fortalecer e aumentar a riqueza / sucesso dos indivíduos mais bem-sucedidos devido ao mecanismo de feedback positivo, que é semelhante ao processo de "enriquecer rico" (também conhecido como "efeito Matthew" [57, 58, 59]) , com um resultado injusto.

Vamos imaginar, por exemplo, um conselho de pesquisa e desenvolvimento financiado pelo governo com uma quantia fixa de dinheiro à sua disposição. O que será muito mais eficaz para aumentar a eficácia média da pesquisa: conceder grandes doações a apenas alguns cientistas sem dúvida excelentes ou pequenas doações a muitos cientistas obviamente mais comuns? Um estudo recente [44], baseado em uma análise de quatro índices do significado científico de publicações relacionadas, descobriu que o significado tem apenas uma fraca relação positiva com o financiamento. Em particular, a importância do dólar foi menor para os grandes doadores, e a importância dos cientistas que receberam aumentos no financiamento não aumentou em um grau apropriado. Os autores do estudo concluíram que o significado científico (conforme refletido na publicação) limita-se apenas ao financiamento e sugeriram que estratégias de financiamento destinadas a diversificar idéias em vez de "excelência" provavelmente serão mais produtivas. Uma contribuição posterior [60] mostrou que, tanto no número de documentos produzidos quanto em sua importância científica, o financiamento concentrado da pesquisa geralmente leva a retornos marginais decrescentes e também que os pesquisadores mais financiados não se destacam em termos de eficácia e significado científico. Em geral, essas conclusões não devem surpreender à luz de outra descoberta recente [18], que afirma que o significado, medido por publicações influentes, é distribuído aleatoriamente por várias publicações do cientista. Em outras palavras, a sorte importa, e se isso afeta mais do que queremos admitir, não surpreende que as estratégias meritocráticas sejam menos eficazes do que o esperado, especialmente se estamos tentando apreciar o mérito de a posteriori. Em estudos anteriores [48, 49, 50, 51, 52, 53, 54, 55] já havia um alerta contra esse tipo de “quase meritocracia”, mostrando a eficácia de estratégias alternativas baseadas em eleições aleatórias nas áreas de gestão, política e finanças. De acordo com esse ponto de vista, o modelo TPU mostra como o nível mínimo de sucesso pode ser aumentado para as pessoas mais talentosas do mundo, onde a sorte importa, e a descoberta acidental geralmente leva a conquistas importantes.

3.1 Descoberta acidental, inovação e estratégias eficazes de financiamento


O termo “descoberta acidental” é amplamente usado em referências literárias a fatos históricos, mostrando que os pesquisadores muitas vezes fazem descobertas inesperadas e úteis por puro acaso, quando procuram algo mais [61, 62]. Há uma longa lista de histórias de descobertas feitas exclusivamente por coincidência: da penicilina de Alexander Fleming à radioatividade de Marie Curie, da radiação cósmica de fundo por microondas dos astrônomos de rádio Arno Penzias e Robert Woodrow Wilson ao grafite Andrei Geim e Konstantin Novosyolov. Aqui está um exemplo mais recente: uma rede de canais cheios de líquido no corpo humano, um órgão anteriormente desconhecido que aparentemente promove a disseminação de células cancerígenas, foi descoberta por acaso durante uma endoscopia simples [63]. Portanto, muitas pessoas pensam que a pesquisa dirigida pela curiosidade deve sempre ser financiada, uma vez que ninguém realmente pode saber antecipadamente ou prever o que leva a [64].

É possível quantificar o significado da descoberta aleatória? Quais são as maneiras mais eficazes de simular a descoberta aleatória? Pode assumir muitas formas diferentes e é difícil limitar e quantificar. É por isso que, até agora, os estudos acadêmicos consideravam uma descoberta científica acidental, na maioria das vezes, como um conceito filosófico. Mas os tempos estão mudando. O Conselho Europeu de Pesquisa alocou recentemente uma doação de US $ 1,7 milhão ao bioquímico Ohid Yakub sobre o significado da descoberta aleatória na ciência [65]. Yakub descobriu que a descoberta aleatória pode ser classificada em quatro tipos básicos [66] e que pode haver fatores importantes que influenciam sua aparência. Suas descobertas parecem coincidir com idéias de pesquisas anteriores [67, 68, 69, 70, 71, 72], que argumentam que estratégias geralmente aceitas, claramente meritocráticas, que buscam superioridade e suplantam a diversidade parecem estar perdendo e ineficaz. O motivo é que eles rejeitam a priori pesquisas que inicialmente pareciam menos promissoras, mas que, graças, em particular, a uma descoberta aleatória, poderiam a posteriori ser incrivelmente inovadoras.

Sob esse ponto de vista, queremos aplicar o modelo TPU, que expressa naturalmente a sorte (e, consequentemente, a descoberta aleatória) como parâmetro quantitativo da estratégia, a fim de estudar a eficácia de vários cenários de financiamento nesta subseção. Em particular, nas situações em que, como mencionado acima, uma pessoa moderadamente talentosa, mas com sorte é muitas vezes mais bem-sucedida do que indivíduos mais talentosos, mas com azar, é importante avaliar a eficácia das estratégias de financiamento para a capacidade de manter um nível mínimo de sucesso, inclusive para as pessoas mais talentosas que se espera que tragam as idéias mais inovadoras e progressivas.

Começando com os mesmos parâmetros iniciais que foram usados ​​na subseção 2.2, ou seja, N = 1000, m T = 0,6, σ T = 0,1, I = 80, δ t = 6, C (0) = 10, NE = 500, p L = 50% e 100 simulações, vamos imaginar que o capital total disponível de financiamento, F T, seja periodicamente distribuído entre os indivíduos de acordo com vários critérios. Por exemplo, as finanças podem ser emitidas:
  1. Igualmente compartilhados (critérios igualitários) para incentivar a diversidade da pesquisa;
  2. Apenas uma certa porcentagem dos indivíduos mais bem-sucedidos (“melhores”) (critério elitista), anteriormente chamada de meritocracia “próxima”, para a distribuição das finanças entre as pessoas com base no desempenho passado.
  3. Distribuição "premium" entre uma certa proporção dos indivíduos mais bem-sucedidos e o restante, em pequenas partes iguais, sobre o restante (critério misto);
  4. , ( ).

, F T 5 , 40- , F T = 8 . . , P T , 100 , T > m T + σ T , / , .., C end > C (0).

, 2.2. , , , / . , P T0 ≈ 32% T > 0,7 , , / , . , , P T P T0 , . P * T = P T − P T0 . : 100 , P * T 2%. , P * T , 40 , E , , E = P * T / F T .


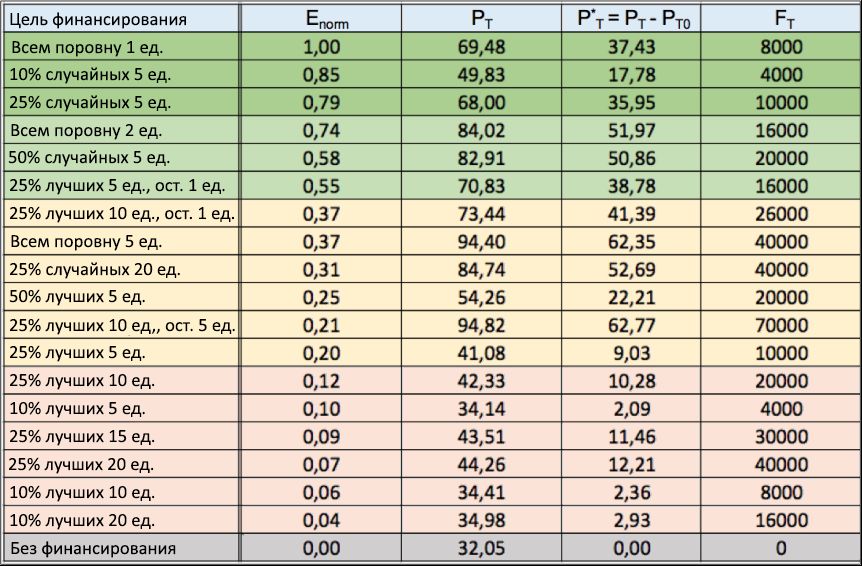
10: . (1 ), E norm (2 ), . , , , P T P * T , « », 100 . , F T , .

, 10, (2- ), , (1 ), P T (3- ) P * T (4- ). , , F T . E E max , () E norm = E / E max . , , E norm = 0. E norm 11. P T , 2%, E norm .

11, , ( ), ( ) , , , .


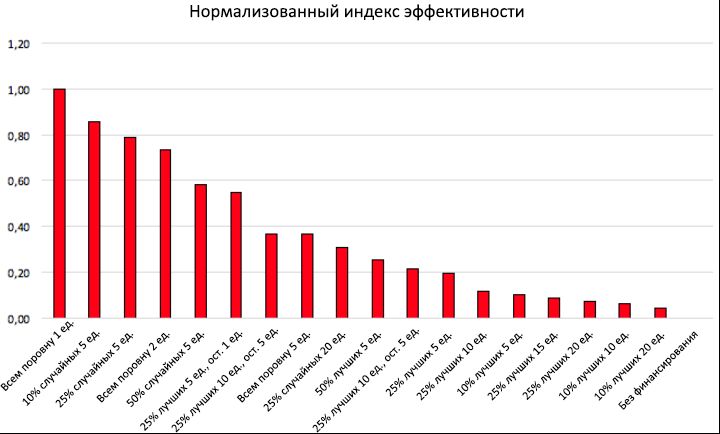
11: . E norm . , , C end > C (0), , , .

, , «» , 1 5 , , E norm = 1 (.., E = E max ): F T 8000 , , « », P T0 = 32,05% P T = 69,48%, P * T = 37,43. (, 2 5 ), ( 69,48% 94,40%), , E norm = 1 E norm = 0,74, E norm = 0,37, .

, «» , 5 (5, 10, 15 20 ) 50%, 25% 10% , , E norm < 0,25 , P * T , « », ( 20%), , . , , , .

, «» , .. «» , , 25%, , , « » , . , «» . , , : 16000 , P T , , , (70,83% 84,02%), E norm (0,55 0,74).

( ), . , , , , : , , .

, , . , , , 5 10% , 4000 , P * T = 17,78%, . , 25% ( 10000 ) P * T= 35,95, comparável ao obtido pela melhor estratégia de equalização, que conquistou o primeiro lugar na classificação geral. É impressionante que este último resultado P * T seja cerca de quatro vezes o valor ( P * T = 9,03%), (. 12 ), (10000 ) (25% ). , , , , , , « » , . , , , , [48, 49, 50, 51, 52, 53, 54, 55], , , .

, 12 . , 100 F T = 80000, 5 F T /8 = 10000 , , , . , , , P T 100%. ( 50% ), , 25% , , , . , , « » .


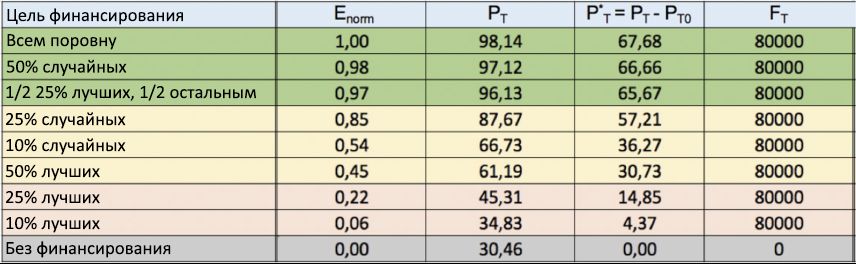
12: . E norm (1- ) , . 10, F T = 80000. .

, , (, , ) , . , , , , .

3.2


, . . , , , , , m T , σ T , , , , .

13 / , 100 , . , 2.2 ( N = 1000, I = 80, δ t = 6, C (0) = 10, N E = 500 p L = 50%), . , (a) m T = 0,6, σ T = 0,2, (b) , σ T = 0,1 m T = 0,7. , .


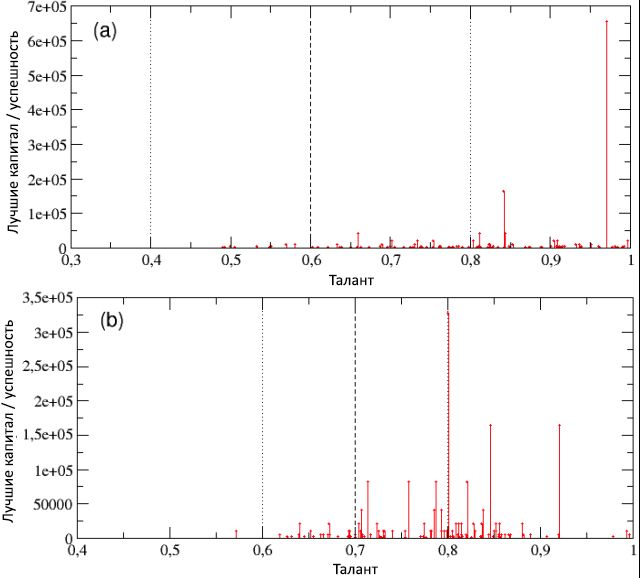
13: 100 , : (a) m T = 0,6 σ T = 0,2 ( ); (b) m T = 0,7 σ T = 0,1 ( ). m T m T ± σ T , , .

, , σ T , m T , (a), – , T = 0,97, / C best = 655360. , , , , , , , . (b) , m T σ T C best = 327680 T = 0,8, , C = 163840 , , T = 0,85 T = 0,92. , , .

, / 100 C mt ≈ 63, 2.2. , C mt ≈ 319 (a) C mt ≈ 122 (b), . , – P T , , .. T > m T + σ T / C end > 10, T > m T + σ T ( , , , m T + σ T = 0,8). , P T = 38% (a) P T = 37,5% (b), P T0 = 32% ( m T = 0,6 σ T = 0,1).

, , , , , , . , , , , . , , , .

, , , , , .. , - , , .

14 , , , , 100 , , 2.2 ( N = 1000, m T = 0,6, σ T = 0,1, I = 80, C (0) = 10, N E = 500) p L (, 2.2 p L = 50%). (a) p L = 80%, , , [26]. , (b) p L = 20% , , , , « ».


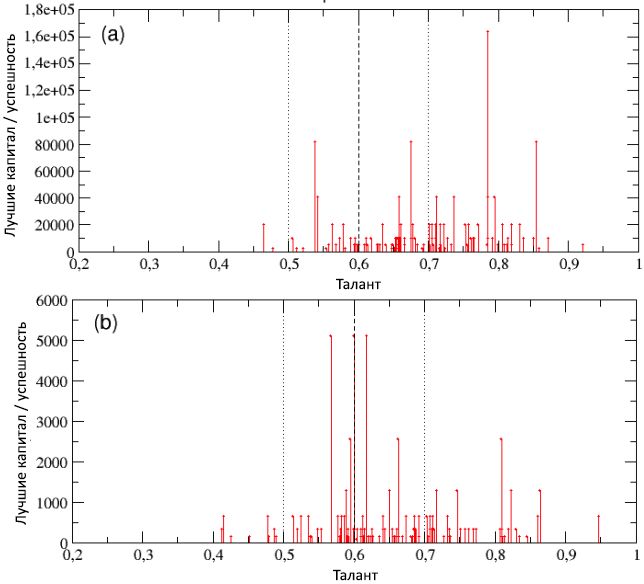
14: 100 , p L : (a) p L = 80%; (b) p L = 20%. , , m T = 0,6 m T ± σ T , σ T = 0,1.

, / , , p L .

p L = 80%, (a), - , p L = 50%, , C best = 163840. , / , C mt ≈ 149, , , P T = 62,18% ( P T0 = 32%), , , , .

p L = 20%. , (b), , , 2.2, C besttotalizando apenas 5120 unidades - esse é um traço de redução das desigualdades sociais, que é a conseqüência esperada da equalização de oportunidades para alcançar o sucesso. De acordo com esses resultados, o indicador P T também atinge um valor mínimo, com uma porcentagem média de indivíduos talentosos que conseguiram aumentar seu nível inicial de sucesso, igual a apenas 8,75%.

, , , , , , . , , , .

4.


, , , . , , , / , 40 , «80/20», , . , , , – , . . , , / , , . , « », , . , – , . , , , .

Agradecimentos


Queremos agradecer a Robert Frank, Pavel Sobkowitz e Konstantino Tsallis pelas discussões e comentários proveitosos.

Bibliografia


  1. Bak, P., Tang, C. e Wiesenfeld, K., Criticidade auto-organizada. Phys. Rev. A , 38: 364 {374 (1988).
  2. Barab´asi, A.-L., Albert, R., Emergence of Scaling in Random Networks, Ciência , vol. 286, Edição 5439, pp. 509 {512 (1999).
  3. Newman, MEJ, leis do poder, distribuições de Pareto e lei de Zipf, Contemporary Physics , 46 (5): 323 {351 (2005).
  4. Tsallis, C., Introdução à Mecânica Estatística Não Extensiva. Aproximando-se de um mundo complexo , Springer (2009).
  5. Pareto, V., Cours d'Economique Politique , vol. 2 (1897).
  6. Steindl, J., Random Processes and the Growth of Firms — A Study of the Pareto Law, Charles Griffin and Company , London (1965).
  7. Atkinson, AB, Harrison, AJ, Distribution of Total Wealth in Britain, Cambridge University Press , Cambridge (1978).
  8. Persky, J., Retrospectives: Pareto's law, Journal of Economic Perspectives 6, 181{192 (1992).
  9. Klass, OS, Biham, O., Levy, M., Malcai, O., Solomon, S., The Forbes 400 and the Pareto wealth distribution, Economics Letters 90, 290{295 (2006).
  10. Hardoon, D., An economy for the 99% , Oxfam GB, Oxfam House, John Smith Drive, Cowley, Oxford, OX4 2JY, UK (January 2017).
  11. Bouchaud, J.-P., M´ezard, M., Wealth condensation in a simple model of economy, Physica A 282, 536{54 (2000).
  12. Dragulescu, A. and Yakovenko, VM, Statistical mechanics of money, Eur. Phys. J. B 17, 723{729 (2000).
  13. Chakraborti, A. and Chakrabarti, BK, Statistical mechanics of money: how saving propensity affects its distribution, Eur. Phys. J. B 17, 167{170 (2000).
  14. Patriarca, M., Chakraborti, A., Germano, G., Influence of saving propensity on the power law tail of wealth distribution, Physica A 369(2), 723{736 (2006).
  15. Scalas, E., Random exchange models and the distribution of wealth. European Physical Journal — Special Topics , 225. pp. 3293-3298. ISSN 1951{6355 (2016).
  16. During, B., Georgiou, N. and Scalas, E., A stylised model for wealth distribution. In Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95{117. ISBN 9789811057045 (2017).
  17. During, Bertram, Georgiou, Nicos and Scalas, Enrico (2017) A stylised model for wealth distribution. In: Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95-117. ISBN 9789811057045
  18. Sinatra, R., Wang, D., Deville, P., Song, C. and Barab´asi, A.-L., Quantifying the evolution of individual scientific impact, Science 354, 6312 (2016).
  19. Einav, L. and Yariv, L., What's in a Surname? The Effects of Surname Initials on Academic Success, Journal of Economic Perspective , Vol. 20, n. 1, p.175{188 (2006).
  20. Ruocco, G., Daraio, C., Folli, V. and Leonetti, M., Bibliometric indicators: the origin of their log-normal distribution and why they are not a reliable proxy for an individual scholar's talent, Palgrave Communications 3:17064 doi: 10.1057/palcomms.2017.64 (2017).
  21. Jurajda, S., Munich, D., Admission to Selective Schools, Alphabetically, Economics of Education Review , Vol. 29, n. 6, p.1100{1109 (2010).
  22. Van Tilburg, WAP, Igou, ER, The impact of middle names: Middle name initials enhance evaluations of intellectual performance, European Journal of Social Psychology , Vol. 44, Issue 4, p.400{411 (2014).
  23. Laham, SM, Koval, P., Alter, AL, The name-pronunciation effect: Why people like Mr. Smith more than Mr. Colquhoun, Journal of Experimental Social Psychology 48, p.752{756 (2012).
  24. Silberzahn, R., Uhlmann, EL, It Pays to be Herr Kaiser: Germans with Noble-Sounding Last Names More Often Work as Managers, Psychological Science 24(12): 2437{44 (2013).
  25. Coffey, B. and McLaughlin, P., From Lawyer to Judge: Advancement, Sex, and NameCalling. SSRN Electronic Journal , DOI10.2139/ssrn.1348280 (2009).
  26. Milanovic, B., Global Inequality of Opportunity: How Much of Our Income Is Determined by Where We Live?, Review of Economics and Statistics , 97.2 (2015): 452{60.
  27. Du, Q., Gao, H., Levi, MD, The relative-age effect and career success: Evidence from corporate CEOs, Economics Letters 117(3):660{662 (2012).
  28. Deaner, RO, Lowen, A., Cobley, S., Born at the Wrong Time: Selection Bias in the NHL Draft. PLoS ONE 8(2): e57753 (2013).
  29. Brooks, D., The Social Animal. The Hidden Sources of Love, Character, and Achievement, Random House , 424 pp. (2011).
  30. Iacopini, I., Milojevic, S. and Latora, V., Network Dynamics of Innovation Processes, Physical Review Letters 120, 048301 (2018).
  31. Tomasetti, C., Li, L., Vogelstein, B., Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention, Science 355, 1330{1334 (2017).
  32. Newgreen, DF et al., Differential Clonal Expansion in an Invading Cell Population: Clonal Advantage or Dumb Luck?, Cells Tissues Organs 203:105{113 (2017).
  33. Snyder, RE and Ellner, SP, We Happy Few: Using Structured Population Models to Identify the Decisive Events in the Lives of Exceptional Individuals, The American Naturalist 188, no. 2 (2016): E28{E45.
  34. Snyder, RE and Ellner, SP, Pluck or Luck: Does Trait Variation or Chance Drive Variation in Lifetime Reproductive Success?, The American Naturalist 191, no. 4 (2018): E90{E107.
  35. .., . , , (2018).
  36. .., . , (2018).
  37. Mauboussin, MJ, The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, Harvard Business Review Press (2012).
  38. .., . , (2019).
  39. Watts, DJ, Everything Is Obvious: Once You Know the Answer , Crown Business (2011).
  40. Salganik, MJ, Dodds PS, Watts DJ, Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market, Science Vol.311 (2006)
  41. Travis, M., Hofman, JM, Sharma, A., Anderson,. A., Watts, DJ, Exploring limits to prediction in complex social systems , Proceedings of the 25th ACM International World Wide Web Conference (2016) arXiv:1602.01013 [cs.SI]
  42. Stewart, J., The Distribution of Talent, Marilyn Zurmuehlin Working Papers in Art Education 2 : 21-22 (1983).
  43. Sinha, S. and Pan, RK, How a «Hit» is Born: The Emergence of Popularity from the Dynamics of Collective Choice, In Econophysics and Sociophysics: Trends and Perspectives (eds BK Chakrabarti, A. Chakraborti and A. Chatterjee), Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany. doi: 10.1002/9783527610006.ch15 (2006).
  44. Fortin, J.-M., Curr, DJ, Big Science vs. Little Science: How Scientific Impact Scales with Funding, PLoS ONE 8(6): e65263 (2013).
  45. Jacob, BA, Lefgren, L., The impact of research grant funding on scientific productivity, Journal of Public Economics 95 (2011) 1168{1177.
  46. O'Boyle, JR. E. and Aguinis, H., The Best and the Rest: revisiting the norm of normality of individual performance, Personnel Psychology , 65: 79-119. doi:10.1111/j.1744-6570.2011.01239.x (2012).
  47. Denrell, J. and Liu, C., Top performers are not the most impressive when extreme performance indicates unreliability, Proceedings of the National Academy of Sciences , 109(24):9331{9336 (2012).
  48. Pluchino, A., Rapisarda, A., and Garofalo, C., The Peter principle revisited: A computational study, Physica A 389(3):467{472 (2010).
  49. Pluchino, A., Garofalo, C., Rapisarda, A., Spagano, S. and Caserta, M., Accidental politicians: How randomly selected legislators can improve parliament efficiency, Physica A 390(21):3944{3954 (2011).
  50. Pluchino, A., Rapisarda, A. and Garofalo, C., Efficient promotion strategies in hierarchical organizations, Physica A 390(20):3496{3511 (2011).
  51. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Reducing financial avalanches by random investments, Phys. Rev. E 88(6):062814 (2013).
  52. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Are random trading strategies more successful than technical ones, PLoS One 8(7):e68344 (2013)
  53. Biondo, AE, Pluchino, A., Rapisarda, A., The beneficial role of random strategies in social and financial systems, J. Stat. Phys. 151(3-4):607{622 (2013).
  54. Biondo, AE, Pluchino, A., Rapisarda, A., Micro and macro benefits of random investments in financial markets, Cont. Phys. 55(4):318{334 (2014).
  55. Biondo, AE, Pluchino, A., Rapisarda, A., Modeling financial markets by self-organized criticality, Phys. Rev. E 92(4):042814 (2015).
  56. Wilensky, U., NetLogo. ccl.northwestern.edu/netlogo . Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999).
  57. Merton, RK, The Matthew effect in science, Science 159, 56-63 (1968).
  58. . ., , II: , https://www.hse.ru/data/033/314/1234/3_6_1Merto.pdf .
  59. Bol, T., de Vaan, M. and van de Rijt, A., The Matthew effect in science funding, Proceedings of the National Academy of Sciences , DOI: 10.1073/pnas.1719557115 (2018).
  60. Mongeon, P., Brodeur, C., Beaudry, C. et al., Concentration of research funding leads to decreasing marginal returns, Research Evaluation 25, 396{404 (2016).
  61. Merton, RK, Barber, E., The Travels and Adventures of Serendipity , Princeton University Press, Princeton (2004).
  62. Murayama, K. et al., Management of science, serendipity, and research performance, Research Policy 44 (4), 862{873 (2015).
  63. Benias, PC et al., Structure and Distribution of an Unrecognized Interstitium in Human Tissues, Scientific Reports , vol. 8, 4947 (2018).
  64. Flexner, A, The Usefulness of Useless Knowledge , Princeton University Press, Princeton (2017).
  65. Lucky science. Scientists often herald the role of serendipity in research. A project in Britain aims to test the popular idea with evidence. , Nature Editorial, Vol.554, 1 February 2018.
  66. Yaqub, O., Serendipity: Towards a taxonomy and a theory, Research Policy 47, 169{179 (2018).
  67. Page, SE, The Diversity Bonus. How Great Teams Pay Off in the Knowledge Economy , Princeton University Press (2017).
  68. Cimini, G., Gabrielli, A., Sylos Labini, F., The Scientific Competitiveness of Nations, PLoS ONE 9(12): e113470. doi.org/10.1371/journal.pone.0113470 (2014).
  69. Curry, S., Let's move beyond the rhetoric: it's time to change how we judge research, Nature 554, 147 (2018).
  70. Nicholson, JM and Ioannidis, JPA, Research grants: Conform and be funded, Nature 492, 34{36 (2012).
  71. Bollen, J., Crandall, D., Junk, D. et al., An efficient system to fund science: from proposal review to peer-to-peer distributions, Scientometrics 110, 521{528 (2017).
  72. Garner, HR, McIver, LJ and Waitzkin, MB, Research funding: Same work, twice the money?, Nature 493,599{601 (2013).


: Talent vs Luck: the role of randomness in success and failure

Source: https://habr.com/ru/post/pt455064/

More articles:


All Articles