Sobre o uso de métodos paramétricos de estimativa espectral em radar - o método MUSIC. Adição ao artigo

Encontrei um bom artigo sobre o método de estimativa espectral, o que é ótimo para um sinal curto da soma de harmônicos de baixo ruído. (-cópia) Talvez meus comentários ajudem o leitor a entender a essência do método. O que me chateou um pouco foram os recursos incompletos do método. O método é usado para o radar - para determinar rapidamente a direção dos sinais de entrada (ângulo θ) com o objetivo subsequente de adaptação automática, deve-se entender, adaptação do sistema. Mas - o autor não produz uma definição numérica desse ângulo (e isso é estranho no contexto), embora essa definição seja bem possível. Temos apenas gráficos bonitos, segundo os quais, ao que parece, o sistema ainda precisa “rastrear” e “rastrear”, determinando o número e a localização dos máximos, o que não é totalmente bom.


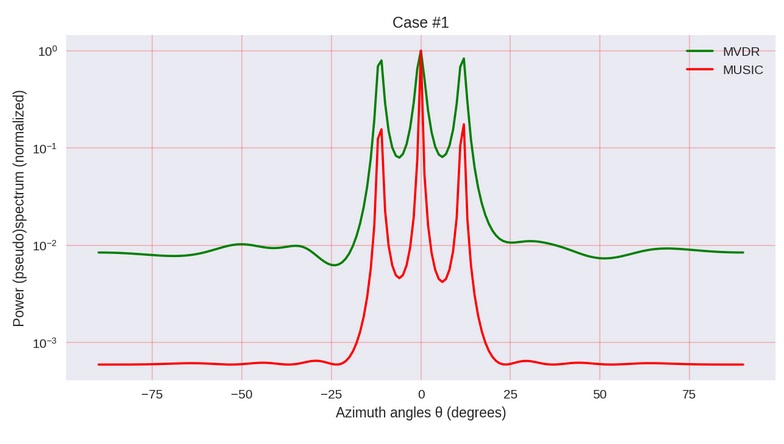Ilustração do autor do artigo mencionado

"Declaração do problema"

Em resumo: precisamos determinar, de alguma forma, onde (em que ângulo) o sinal vem da antena treliça. Depois, ajuste-o na direção - mas isso não está mais nesta "música".

"Modelando o sinal recebido"



(não é importante - aparentemente, o "símbolo" deve ser lido em todos os lugares como um "sinal")

Aqui, tenha cuidado. O autor parece estar trabalhando com um certo sinal complexo (espacial). Embora X , sim, possa ser, como está escrito, uma matriz de "amplitudes complexas" (dependendo não da coordenada, mas da frequência espacial), mas, por exemplo, XX ^H são "covariâncias" e não "densidades espectrais".

S é mais semelhante à matriz de “amplitudes complexas”, com a ajuda de quais componentes harmônicos (sinal útil) são modelados. Nem ruídos aditivos, nem, ao que parece, nem mesmo componentes harmônicos são um sinal analítico aqui. Embora os harmônicos, com reservas, estejam muito próximos disso.



"# Fórmula geral:
# sqrt (N0 / 2) * (G1 + jG2),
# onde G1 e G2 são processos gaussianos independentes. ”

O principal é de onde o componente imaginário vem de medições reais, de alguma forma não está claro. É possível, em princípio, calcular o sinal analítico.

É possível que exista uma “fonte” onde eles trabalharam com X real (sinal recebido). Por exemplo, o autor parece ter sido muito interessado em "simular" os espectros resultantes (mesmo) - em todos os casos considerados, os sinais de teste são dados pelos sinais que chegam simetricamente à esquerda e à direita.

"Termos"

Determinamos o intervalo de ângulos θ de chegada do sinal, no qual faz sentido olhar. É verdade que, por qualquer motivo, construímos os gráficos de +90 a -90 graus.

"Um pouco de teoria sobre o próprio método"

Adição. A MÚSICA é obtida a partir de estimativas autoregressivas (das equações de Yule-Walker) quase por si só, no caso em que a variação do ruído branco condicional é desprezível. Os resultados são quase os mesmos. A solução SLAE é ainda mais econômica que a busca por vetores próprios, mas, a propósito, por várias razões, a decomposição espectral da matriz de covariância com sua baixa condicionalidade seria muito desejável de qualquer maneira.

EVD, de fato, é simplesmente = "encontrando autovalores e vetores", e nada mais. Não é um algoritmo.

Por que escrevemos um "pseudo-espectro" - porque o espectro só pode ser determinado a partir dos vetores próprios da matriz de covariância (correlação) até um fator de escala, ou seja, os valores absolutos resultantes não fazem sentido. Mas precisamos com precisão e apenas a posição dos máximos.



- Este é o mais interessante. Bem, primeiro, U ₀ já são autovetores, apenas para a matriz de covariância - e o "salvar" em sua pesquisa falhará. Próximo. A busca de soluções levará à necessidade de determinar as raízes da equação de potência, que é absolutamente equivalente a outra decomposição espectral. O autor, aparentemente, confunde os valores próprios de matrizes completamente diferentes.

Mas ... o principal ... agora (!), Finalmente (!), Podemos logaritmos as raízes e determinar numericamente as complexas “impedâncias” (pólos do modelo) (na equação, isso é novamente θ, o que não é muito bom), o que sua parte imaginária mostrará exatamente esse ângulo em que o sinal veio. É muito lamentável que o autor não tenha.

"Modelagem"



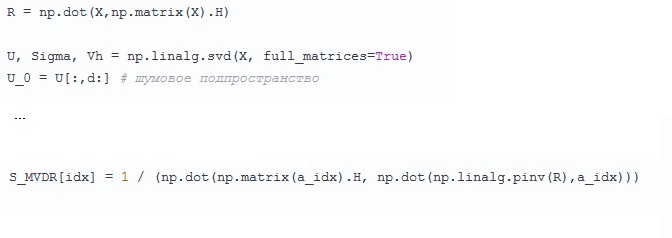
Aqui está um pouco alarmante - a princípio, a matriz de covariância R = XX ^{H foi} calculada, que por algum motivo foi esquecida por algum tempo e começou tudo de novo - decomposta em números e vetores singulares X. Eles prometeram pelo texto procurar os autovalores e o vetor R, que, é claro, é o mesmo, mas como era mais lógico, quando R já foi encontrado. Não está claro qual problema o autor encontrou.

Recordamos R quando avaliamos o espectro usando o método de dispersão mínima MVDR. E aqui também é interessante - R , a julgar pelo script, parece ter sido revertido, em total conformidade com esse método, de maneira clássica, sem nenhum SVD (pseudo-inversão), embora pareça ser de baixa classificação (altamente degenerado). Quero dizer, nossos ruídos são tão pequenos? Bem, talvez.

Realmente confunde aqui isso. O tamanho do "subespaço de ruído" no script parece ser atribuído pela ordem volitiva (igual a d). Mas, no caso real, não sabemos quantos harmônicos existem no sinal e quantos ruídos. Foi necessário analisar esses autovalores - quais deles são insignificantes pequenos, quais não são.

Em geral, o trabalho é muito interessante, e não apenas para radar. O método, acredito, tem um grande potencial, apenas para esses tipos de sinais. O autor funcionou muito bem, e algumas inconsistências irritantes não são tão difíceis de corrigir. E o principal é complementar o artigo com o método RootMUSIC.