Se você não está escrevendo um programa, não use uma linguagem de programação

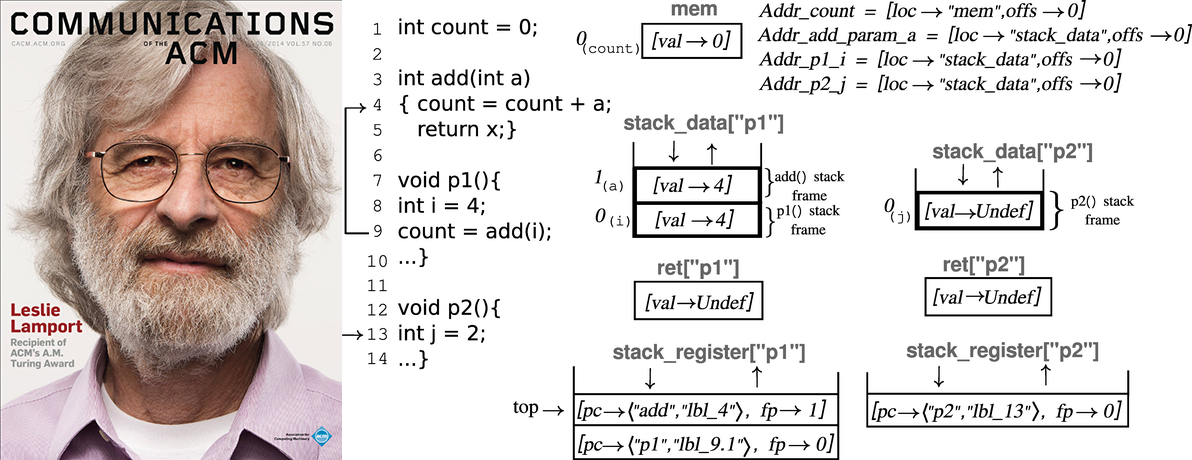
Leslie Lamport é o autor do trabalho fundamental em computação distribuída, e você também pode conhecê-lo pelas letras La em La TeX - "Lamport TeX". Esta é a primeira vez que ele introduziu o conceito de consistência consistente em 1979, e seu artigo “Como fazer um computador multiprocessador que execute corretamente programas multiprocessos” ganhou o prêmio Dijkstra (mais precisamente, em 2000, o prêmio foi chamado da maneira antiga: “PODC Influential Paper Award "). Há um artigo na Wikipedia sobre ele, onde você pode obter alguns links mais interessantes. Se você está satisfeito com a solução de problemas no que acontece antes ou nos problemas dos generais bizantinos (BFT), deve entender que Lamport está por trás de tudo isso.

Esta habrastatya é uma tradução do relatório de Leslie no Fórum do Heidelberg Laureate em 2018. A palestra se concentrará em métodos formais usados ​​no desenvolvimento de sistemas complexos e críticos, como a sonda espacial Rosetta ou os mecanismos da Amazon Web Services. A visualização deste relatório é obrigatória para participar de uma sessão de perguntas e respostas que Leslie realizará na Hydra Conference - essa habrastatia pode economizar uma hora para você assistir a um vídeo. Com esta introdução concluída, passamos a palavra ao autor.

Era uma vez, Tony Hoar escreveu: "Todo grande programa tem um pequeno programa que tenta sair". Eu o reformularia assim: "Em todo programa grande, existe um algoritmo que tenta sair". Não sei, no entanto, se Tony concordaria com essa interpretação.

Considere, por exemplo, o algoritmo euclidiano para encontrar o maior divisor comum de dois números inteiros positivos $$$(M, N)$ . Neste algoritmo, atribuímos $$$x$ valor $$$M$ , $$$N$ - valor $$$y$ e subtraia o menor desses valores do maior até que eles sejam iguais. Significado destes $$$x$ e $$$y$ e será o maior fator comum. Qual é a diferença essencial entre esse algoritmo e o programa que o implementa? Nesse programa, haverá muitas coisas de baixo nível: $$$M$ e $$$N$ haverá um certo tipo, BigInteger ou algo assim; será necessário determinar o comportamento do programa se $$$M$ e $$$N$ não positivo; e assim por diante. Não há clara diferença entre os algoritmos e os programas, mas no nível intuitivo sentimos a diferença - os algoritmos são mais abstratos, de nível superior. E, como eu disse, dentro de cada programa existe um algoritmo que tenta sair. Geralmente, esses não são os algoritmos sobre os quais fomos informados no curso de algoritmos. Como regra, este é um algoritmo que é útil apenas para este programa em particular. Na maioria das vezes, será muito mais complicado do que os descritos nos livros. Tais algoritmos são freqüentemente chamados de especificações. E, na maioria dos casos, esse algoritmo falha ao sair, porque o programador não suspeita de sua existência. O fato é que esse algoritmo não pode ser visto se o seu pensamento estiver focado em código, tipos, exceções, loops de while e mais, e não nas propriedades matemáticas dos números. Um programa escrito dessa maneira é difícil de depurar; portanto, o que significa depurar um algoritmo no nível do código. As ferramentas de depuração foram projetadas para encontrar erros no código e não no algoritmo. Além disso, esse programa será ineficaz, porque, novamente, você otimizará o algoritmo no nível do código.

Como em quase qualquer outro campo da ciência e da tecnologia, esses problemas podem ser resolvidos descrevendo-os matematicamente. Existem muitas maneiras de fazer isso, consideraremos as mais úteis delas. Ele funciona com algoritmos sequenciais e paralelos (distribuídos). Este método consiste em descrever a execução do algoritmo como uma sequência de estados e cada estado como a atribuição de propriedades a variáveis. Por exemplo, o algoritmo euclidiano é descrito como uma sequência dos seguintes estados: primeiro, x recebe o valor M (número 12) e y é o valor N (número 18). Subtraímos o valor menor do maior ( $$$x$ de $$$y$ ), o que nos leva ao próximo estado em que já estamos tirando $$$y$ de $$$x$ , e a execução do algoritmo para com isso: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ .

Chamamos uma sequência de comportamento de estados e um par de estados consecutivos uma etapa. Qualquer algoritmo pode ser descrito por uma variedade de comportamentos que representam todas as variantes possíveis do algoritmo. Para cada M e N específico, existe apenas uma modalidade, portanto, um conjunto de um comportamento é suficiente para descrevê-lo. Algoritmos mais complexos, especialmente paralelos, têm muitos comportamentos.

Muitos comportamentos são descritos, primeiramente, por um predicado inicial para estados (um predicado é apenas uma função com um valor booleano); e, em segundo lugar, um predicado do próximo estado para pares de estados. Algum comportamento $$$s_1, s_2, s_3 ...$ entra em muitos comportamentos somente se o predicado inicial for verdadeiro para $$$s_1$ e os predicados do próximo estado são verdadeiros para cada etapa $$$(s_i, s_ {i + 1})$ . Vamos tentar descrever o algoritmo euclidiano dessa maneira. O predicado inicial aqui é: $$$(x = M) \ terreno (y = N)$ . E o predicado do próximo estado para pares de estados é descrito pela seguinte fórmula:

Não se assuste - existem apenas seis linhas; é muito fácil descobrir se você faz isso em ordem. Nesta fórmula, variáveis ​​sem traços se referem ao primeiro estado e variáveis ​​com traços são as mesmas variáveis ​​no segundo estado.

Como você pode ver, a primeira linha diz que no primeiro caso x é maior que y no primeiro estado. Após um AND lógico, afirma-se que o valor de x no segundo estado é igual ao valor de x no primeiro estado menos o valor de y no primeiro estado. Após outro AND lógico, é afirmado que o valor de y no segundo estado é igual ao valor de y no primeiro estado. Tudo isso significa que, no caso em que x é maior que y, o programa subtrai y de x e deixa y inalterado. As últimas três linhas descrevem o caso em que y é maior que x. Observe que essa fórmula é falsa se x for igual a y. Nesse caso, não há próximo estado e o comportamento é interrompido.

Então, acabamos de descrever o algoritmo euclidiano em duas fórmulas matemáticas - e não tivemos que mexer com nenhuma linguagem de programação. O que poderia ser mais bonito do que essas duas fórmulas? Substitua-os por uma fórmula. Comportamento $$$s_1, s_2, s_3 ...$ é a execução do algoritmo euclidiano apenas se:

• $$$Init_E$ verdadeiro para $$$s_1$ ,
• $$$Next_E$ verdadeiro para cada passo $$$(s_i, s_ {i + 1})$ .

Isso pode ser escrito como um predicado de comportamentos (nós chamaremos de propriedade) da seguinte maneira. A primeira condição pode ser expressa simplesmente como $$$Init_E$ . Isso significa que interpretamos um predicado de estado como verdadeiro para o comportamento apenas se for verdadeiro para o primeiro estado. A segunda condição é escrita da seguinte maneira: $$$\ square Next_E$ . Um quadrado significa a correspondência entre os predicados de pares de estados e os predicados de comportamento, ou seja, $$$Next_E$ verdadeiro para cada passo no comportamento. Como resultado, a fórmula fica assim: $$$Init_E \ land \ square Próximo_E$ .

Então, escrevemos matematicamente o algoritmo euclidiano. Em essência, essas são simplesmente definições ou abreviações para $$$Init_E$ e $$$Next_E$ . Essa fórmula inteira ficaria assim:

Ela não é linda? Infelizmente, para a ciência e a tecnologia, a beleza não é um critério determinante, mas significa que estamos no caminho certo.

A propriedade que anotamos é verdadeira para alguns comportamentos somente se as duas condições que acabamos de descrever forem satisfeitas. At $$$M = 12$ e $$$N = 18$ eles são verdadeiros para o seguinte comportamento: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ . Mas essas condições também são atendidas para versões mais curtas do mesmo comportamento: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6]$ . E não devemos levá-los em consideração, pois são apenas etapas separadas do comportamento que já levamos em consideração. Existe uma maneira óbvia de se livrar deles: simplesmente ignore o comportamento que termina em um estado para o qual pelo menos um próximo passo é possível. Mas essa não é a abordagem correta, precisamos de uma solução mais geral. Além disso, essa condição nem sempre funciona.

Uma discussão sobre esse problema nos leva aos conceitos de segurança e atividade. A propriedade security indica quais eventos são válidos. Por exemplo, o algoritmo tem permissão para retornar o valor correto. A propriedade activity indica quais eventos devem ocorrer mais cedo ou mais tarde. Por exemplo, um algoritmo deve retornar algum valor mais cedo ou mais tarde. Para o algoritmo euclidiano, a propriedade security é a seguinte: $$$Init_E \ land \ square Próximo_E$ . Uma propriedade de atividade deve ser adicionada a isso para evitar paradas prematuras: $$$Init_E \ land \ square Próximo_E \ land L$ . Nas linguagens de programação, na melhor das hipóteses, há alguma definição primitiva de atividade. Na maioria das vezes, a atividade nem é mencionada; está simplesmente implícito que o próximo passo no programa deve acontecer. E para adicionar essa propriedade, você precisa de um código bastante complicado. Matematicamente, é muito fácil expressar atividade (apenas esse quadrado é necessário para isso), mas, infelizmente, não tenho tempo para isso - teremos que limitar nossa discussão à segurança.

Uma pequena digressão apenas para matemáticos: cada propriedade é um conjunto de comportamentos para os quais essa propriedade é verdadeira. Para cada conjunto de seqüências, existe uma topologia natural que a seguinte função de distância cria:

$$$s = 17, \ sqrt {2}, -2, \ pi, 10, 1/2 \\ t = 17, \ sqrt {2}, -2, e, 10, 1/$

A distância entre essas duas funções é ¼, pois a primeira diferença entre elas está no quarto elemento. Consequentemente, quanto maior a porção em que essas seqüências são idênticas, mais próximas elas estão. Essa função por si só não é tão interessante, mas cria uma topologia muito interessante. Nesta topologia, propriedades de segurança são conjuntos fechados e propriedades de atividade são conjuntos densos. Na topologia, um dos teoremas fundamentais afirma que cada conjunto é a interseção de um conjunto fechado e um conjunto denso. Se lembrarmos que propriedades são conjuntos de comportamentos, segue-se desse teorema que cada propriedade é uma conjunção de uma propriedade de segurança e uma propriedade de atividade. Esta é uma conclusão que também será interessante para os programadores.

Correção parcial significa que o programa pode parar apenas se der a resposta correta. A correção parcial do algoritmo euclidiano diz que se ele completou a execução, então $$$x = GCD (M, N)$ . E nosso algoritmo completa a execução se $$$x = y$ . Em outras palavras, $$$(x = y) \ Rightarrow (x = GCD (M, N))$ . A correção parcial desse algoritmo significa que essa fórmula é verdadeira para todos os estados de comportamento. Adicione um símbolo ao início $$$\ quadrado$ o que significa "para todas as etapas". Como você pode ver, não há variáveis ​​com um traço na fórmula; portanto, sua verdade depende do primeiro estado em cada etapa. E se algo é verdadeiro para o primeiro estado de cada etapa, essa afirmação é verdadeira para todos os estados. A correção parcial do algoritmo euclidiano é satisfeita por qualquer comportamento aceitável para o algoritmo. Como vimos, o comportamento é permitido se a fórmula apresentada é verdadeira. Quando dizemos que uma propriedade é satisfeita, significa simplesmente que essa propriedade segue de alguma fórmula. Isso não é maravilhoso? Aqui está:

$$$Init_E \ land \ square Próximo_E \ Rightarrow \ square ((x = y) \ Rightarrow (x = GCD (M, N)))$

Nos voltamos para a invariância. O quadrado com colchetes depois de ser chamado de propriedade de invariância :

$$$Init_E \ land \ square Próximo_E \ Rightarrow \ color {vermelho} {\ square ((x = y) \ Rightarrow (x = GCD (M, N)))}$

O valor entre colchetes após o quadrado é chamado de invariante :

$$$Init_E \ land \ square Próximo_E \ Rightarrow \ square (\ color {red} {{x = y) \ Rightarrow (x = GCD (M, N))})$

Como provar a invariância? Provar $$$Init_E \ land \ square Próximo_E \ Rightarrow \ square I_E$ , você precisa provar que, para qualquer comportamento $$$s_1, s_2, s_3 ...$ a consequência $$$Init_E \ land \ square Próximo_E$ é verdade $$$I_e$ para qualquer condição $$$s_j$ . Podemos provar isso por indução, para isso precisamos provar o seguinte:

1. de $$$Init_E \ land \ square Próximo_E$ segue-se que $$$I_e$ verdadeiro para o estado $$$s_1$ ;
2. de $$$Init_E \ land \ square Próximo_E$ segue-se que se $$$I_e$ verdadeiro para o estado $$$s_j$ então também
   verdadeiro para o estado $$$s_ {j + 1}$ .

Primeiro precisamos provar que $$$Init_E$ implica $$$I_e$ . Porque a fórmula afirma que $$$Init_E$ verdadeiro para o primeiro estado, isso significa que $$$I_e$ verdadeiro para o primeiro estado. Além disso, quando $$$Next_E$ verdadeiro para qualquer etapa e $$$I_e$ fiel a $$$s_j$ , $$$I_e$ verdadeiro para $$$s_ {j + 1}$ porque $$$\ square Next_E$ significa que $$$Next_E$ verdadeiro para qualquer par de estados. Isto está escrito assim: $$$Próximo_E \ terra I_E \ Rightarrow I'_E$ onde $$$I'_E$ É isso $$$I_e$ para todas as variáveis ​​com um acidente vascular cerebral.

Um invariante que atenda às duas condições que acabamos de provar é chamado de invariante indutivo . A correção parcial não é indutiva. Para provar sua invariância, você precisa encontrar a invariante indutiva que a implica. No nosso caso, a invariante indutiva será a seguinte: $$$GCD (x, y) = GCD (M, N)$ .

Cada ação subsequente do algoritmo depende de seu estado atual, e não de ações passadas. O algoritmo satisfaz a propriedade de segurança, uma vez que a invariante indutiva é preservada nela. O algoritmo euclidiano pode calcular o maior denominador comum (ou seja, ele não para até ser atingido) devido ao fato de possuir um invariante $$$GCD (x, y) = GCD (M, N)$ . Para entender o algoritmo, você precisa conhecer seu invariante indutivo. Se você estudou a verificação do programa, sabe que a prova do invariante que acabamos de fornecer nada mais é do que um método para provar a correção parcial dos programas seqüenciais do Floyd-Hoare. Você também deve ter ouvido falar do método Hoviki - Gris , que é a extensão do método Floyd-Hoar para programas paralelos. Nos dois casos, a invariante indutiva é gravada usando a anotação do programa. E se você fizer isso com a ajuda da matemática, e não com uma linguagem de programação, isso é feito de maneira extremamente simples. É isso que está no cerne do método Oviki-Gris. A matemática torna os fenômenos complexos muito mais acessíveis para a compreensão, embora os próprios fenômenos, é claro, não sejam mais simples.

Dê uma olhada nas fórmulas. Se em matemática escrevemos uma fórmula com variáveis $$$x$ e $$$y$ , isso não significa que outras variáveis ​​não existem. Você pode adicionar outra equação na qual $$$y$ colocado em relação a $$$z$ , isso não mudará nada. Apenas a fórmula não diz nada sobre outras variáveis. Eu já disse que um estado é uma atribuição de valores a variáveis, agora você pode adicionar a isso: com todas as variáveis ​​possíveis, iniciando $$$x$ e $$$y$ e terminando com a população do Irã. Devo confessar: quando eu disse que a fórmula $$$Init_E \ land \ square Próximo_E$ descreve o algoritmo euclidiano, eu menti. Na verdade, descreve um universo em que significados $$$x$ e $$$y$ representam a execução do algoritmo euclidiano. A segunda parte da fórmula ( $$$\ square Next_E$ ) afirma que cada etapa é alterada $$$x$ ou $$$y$ . Em outras palavras, descreve um universo no qual a população do Irã só pode mudar se o significado mudar $$$x$ ou $$$y$ . Daqui se conclui que no Irã ninguém pode nascer após a execução do algoritmo euclidiano. Obviamente, isso não é verdade. Este erro pode ser corrigido se tivermos etapas válidas para as quais $$$x$ e $$$y$ permanecem inalterados. Portanto, precisamos adicionar mais uma parte à nossa fórmula: $$$Init_E \ land \ square (Próximo_E \ lor (x '= x) \ land (y' = y))$ . Para resumir, escrevemos assim: $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ . Esta fórmula descreve um universo contendo o algoritmo euclidiano. As mesmas alterações devem ser feitas na prova do invariante:

• Nós provamos: $$$Init_E \ land \ color {red} {\ square [Próximo_E] _ {<x, y>}} \ Rightarrow \ square I_E$
• Com a ajuda de:
  
  1. $$$Init_E \ Rightarrow I_E$
  2. $$$\ color {red} {\ square [Next_E] _ {<x, y>}} \ land I_E \ Rightarrow I'_E$

Essa mudança é responsável pela segurança do algoritmo euclidiano, já que agora são possíveis comportamentos nos quais valores $$$x$ e $$$y$ não mude. Esses comportamentos devem ser eliminados usando a propriedade de atividade. Isso é bem simples, mas não vou falar sobre isso agora.

Fale sobre implementação. Suponha que tenhamos algum tipo de máquina que implementa o algoritmo euclidiano como um computador. Representa números como matrizes de palavras de 32 bits. Para operações simples de adição e subtração, ela precisa de muitas etapas, como um computador. Se você ainda não toca na atividade, também podemos imaginar essa máquina pela fórmula $$$Init_ {ME} \ land \ square [Próximo_ {ME}] _ {<...>}$ . O que queremos dizer quando dizemos que a máquina euclidiana implementa o algoritmo euclidiano? Isso significa que a seguinte fórmula está correta:

Não se assuste, vamos agora examiná-lo em ordem. Ele diz que nossa máquina satisfaz algumas propriedades ( $$$\ Rightarrow$ ) Esta propriedade é a fórmula euclidiana. $$$(Init_E \ land \ square [Next_E] _ {<x, y>}$ , dots são expressões que contêm variáveis ​​de máquina euclidianas e $$$WITH$ É uma substituição. Em outras palavras, a segunda linha é a fórmula euclidiana na qual $$$x$ e $$$y$ substituído por pontos. Em matemática, não existe uma notação universalmente aceita para substituição, então eu tive que inventar ela mesma. Essencialmente, a fórmula euclidiana ( $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ ) É uma abreviação para a fórmula:

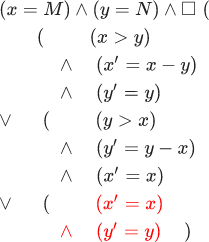
Parte destacada em vermelho da fórmula, permitindo $$$x$ e $$$y$ em $$$(Init_E \ land \ square [Next_E] _ {\ color {red} {<x, y>}}$ continue o mesmo.

A expressão descrita afirma não apenas que a máquina implementa o algoritmo euclidiano, mas também que isso é feito considerando as substituições especificadas. Se você apenas pegar alguns programas e disser que as variáveis ​​desses programas estão relacionadas a $$$x$ e $$$y$ - não faz sentido dizer que tudo isso "implementa o algoritmo euclidiano". É necessário indicar exatamente como o algoritmo será implementado, porque, após todas as permutações, a fórmula se tornará verdadeira. Agora não tenho tempo para mostrar que a definição descrita acima está correta, você deve aceitar minha palavra. Mas acho que você já apreciou o quão simples e elegante é. A matemática é realmente bonita - com ela conseguimos determinar o que significa que um algoritmo implementa outro.

Para provar isso, é necessário encontrar um invariante adequado $$$I_ {ME}$ Carros euclidianos. Para fazer isso, as seguintes condições devem ser atendidas:

1. $$$Init_ {ME} \ Rightarrow (Init_E, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$
2. $$$I_ {ME} \ land [Próximo_ {ME}] _ {<...>} \ Rightarrow ([Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow. ..)$

Não vamos nos aprofundar nelas agora, apenas preste atenção ao fato de que essas são fórmulas matemáticas comuns, embora não sejam as mais simples. Invariante $$$I_ {ME}$ explica por que a máquina euclidiana implementa o algoritmo euclidiano. Implementação significa substituir expressões por variáveis. Esta é uma operação matemática muito comum. Mas no programa, essa substituição não pode ser executada. Você não pode substituir a + b no lugar de x na expressão de atribuição x = … , esse registro não fará sentido. Então, como determinar se um programa implementa outro? Se você pensa apenas em termos de programação, isso não é possível. Na melhor das hipóteses, você pode encontrar algumas definições complicadas, mas uma maneira muito melhor é traduzir os programas em fórmulas matemáticas e usar a definição que eu dei acima. Traduzir um programa em uma fórmula matemática é fornecer a semântica do programa. Se a máquina euclidiana é um programa, e $$$Init_ {ME} \ land \ square [Próximo_ {ME}] _ {<...>}$ - sua notação matemática, então $$$(Init_E \ land \ square [Next_E] _ {<x, y>}, WITH \ thinspace x \ leftarrow ..., y \ leftarrow ...)$ mostra-nos que isso significa que "o programa implementa o algoritmo euclidiano". As linguagens de programação são muito complexas; portanto, essa tradução do programa em uma linguagem matemática também é complicada; portanto, na prática, não. Simplesmente, as linguagens de programação não são projetadas para escrever algoritmos nelas. , , , : , x y , . , , , .

- : , , , . , . — . . , . , — , . :

. $$$DecrementX$ :

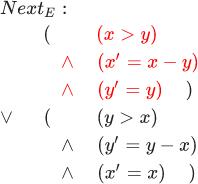
— $$$DecrementY$ :

, :

.

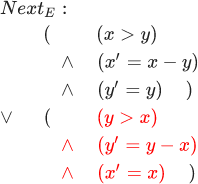
. Rosetta — , . Virtuoso. . TLA+, . , , . , (Eric Verhulst), . , TLA+, : « TLA+ . - C. TLA+ Virtuoso». . . , , , . . TLA+. , .

. Communications of the ACM ] , - Amazon . Amazon Web Services — , Amazon. , — TLA+. . -, , . , , . -, , . , — , , . -, , Amazon , . , 10% TLA+.

— Microsoft. TLA+ 2004 . 2015 TLA+, . . Amazon Web Services. Microsoft , , . : « , ». , Microsoft - . : « ». 2016-17 . TLA+, 150 , Azure ( Microsoft). Azure 2018 , , . : « , . , ». , , . - : , . , , .

, TLA+ . , TLA+, TLA+ Azure, , TLA+. , . , TLA+ , . Microsoft Cosmos DB, , . , . TLA+, , , TLA+.

TLA+ — . . TLA+ . , , . TLA+ , . : TLA+ , .

, . , , . , . Amazon Microsoft , . , .

, . — , . , Hydra 2019, 11-12 2019 -. .