🤲 ➰ 👐🏽 Filtragem linear ideal: de descida gradiente a filtros adaptativos ✌🏾 😙 🙍

Desenvolvendo o tópico de resumos na especialidade do mestrado "Comunicação e processamento de sinais" (TU Ilmenau), gostaria de continuar um dos principais tópicos do curso "Processamento de sinais adaptativos e de matriz" . Ou seja, o básico da filtragem adaptativa.

Para quem este artigo foi escrito:

1) para uma irmandade estudantil de uma especialidade nativa ;
2) para professores que preparam seminários práticos, mas ainda não decidiram as ferramentas - abaixo estão exemplos em python e Matlab / Octave ;
3) para qualquer pessoa interessada no tópico de filtragem.

O que pode ser encontrado sob o corte:

1) informações da teoria, que tentei organizar da maneira mais concisa possível, mas, ao que me parece, informativamente;
2) exemplos do uso de filtros: em particular, como parte do equalizador para o conjunto de antenas;
3) links para literatura básica e bibliotecas abertas (em python), que podem ser úteis para pesquisas.

Em geral, seja bem-vindo e vamos resolver tudo por pontos.

A pessoa pensativa na foto é familiar para muitos, eu acho, Norbert Wiener. Na maior parte, estudaremos o filtro de seu nome. No entanto, não podemos deixar de mencionar nosso compatriota - Andrei Nikolaevich Kolmogorov, cujo artigo de 1941 também contribuiu significativamente para o desenvolvimento da teoria ideal de filtragem, que mesmo em fontes inglesas é chamada de teoria de filtragem Kolmogorov-Wiener .

O que estamos considerando?

Hoje, estamos considerando um filtro clássico com uma resposta de impulso finito (FIR, resposta de impulso finito), que pode ser descrita pelo seguinte circuito simples (Fig. 1).

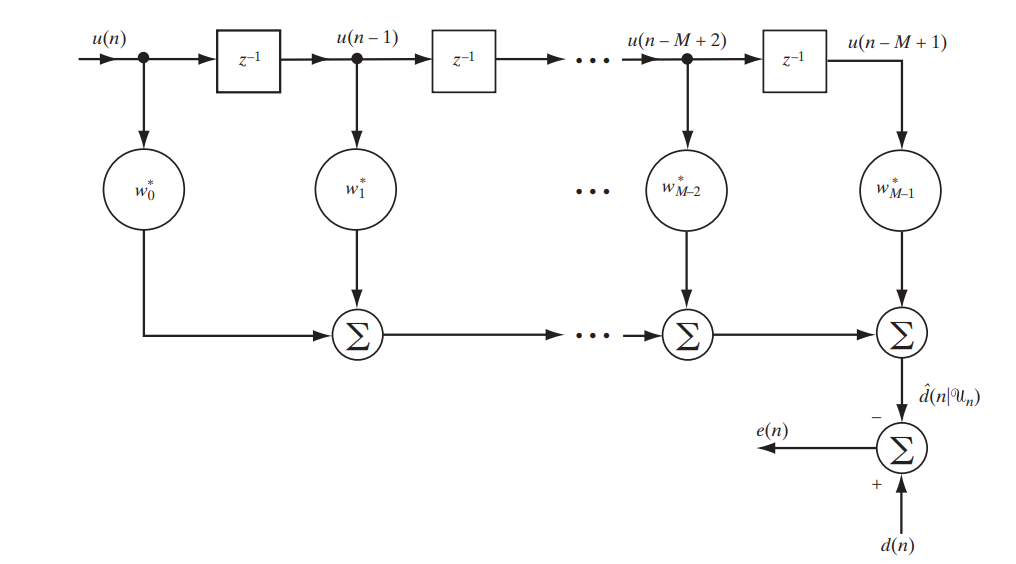
Fig. 1. O esquema do filtro FIR para estudar o filtro Wiener. [1. p.117]

Escreveremos em forma de matriz o que exatamente estará na saída deste estande:

$e (n) = d (n) - \ hat {d} (n | \ mathcal {U} _n) = d (n) - \ mathbf {w} ^ H \ mathbf {u} \ qquad (1)$

Decifre a notação:

É a diferença (erro) entre os sinais dados e os recebidos
Algum sinal predefinido
$\ mathbf {u}$ É um vetor de amostras ou, em outras palavras, um sinal na entrada do filtro
$\ hat {d} (n | \ mathcal {U} _n)$ O sinal está na saída do filtro
$\ mathbf {w} ^ H$ - esta é uma conjugação hermitiana do vetor do coeficiente do filtro - é na seleção ideal deles que se encontra a adaptabilidade do filtro

Você provavelmente já adivinhou que procuraremos a menor diferença entre o sinal fornecido e o filtrado, ou seja, o menor erro. Isso significa que estamos enfrentando uma tarefa de otimização.

O que vamos otimizar?

Para otimizar, ou melhor, minimizar, não queremos dizer apenas o erro, o erro quadrado médio ( MSE - Mean Sqared Error ):

$MSE: J (\ mathbf {w}) = E \ {e (n) ^ 2 \} \ qquad (2)$

onde $J (\ mathbf {w})$ denota a função de custo do vetor de coeficientes de filtro e $E \ {* \}$ denota tapete. esperando.

A praça neste caso é muito agradável, pois significa que estamos diante do problema da programação convexa (pesquisei apenas um análogo da otimização convexa inglesa), o que, por sua vez, implica um único extremo (no nosso caso, no mínimo).

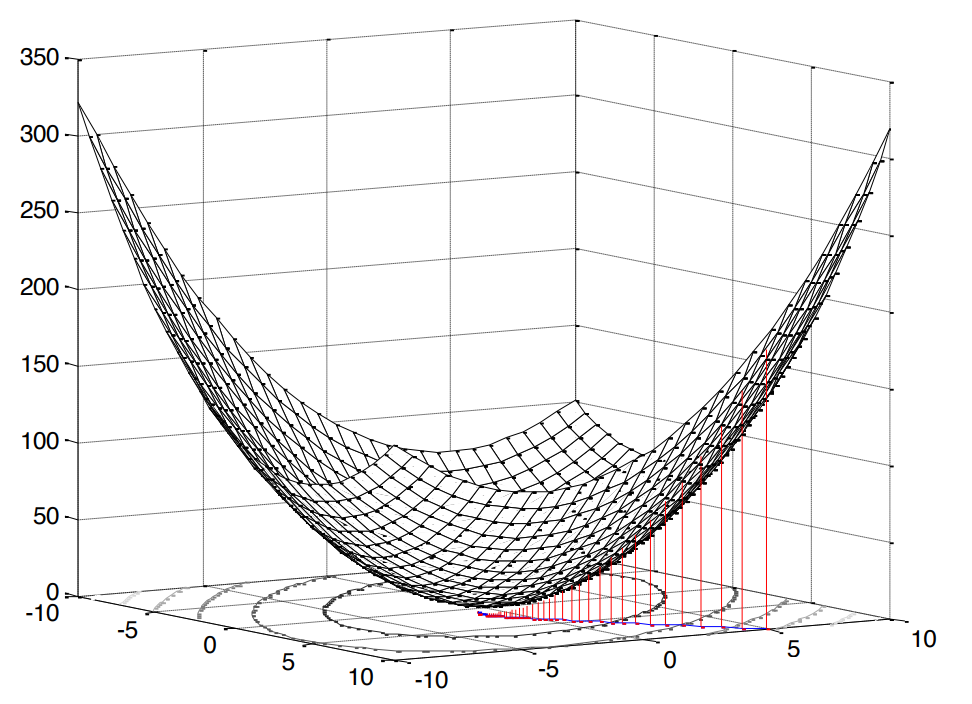
Fig. 2. A superfície do erro quadrático médio .

Nossa função de erro tem uma forma canônica [1, p. 121]:

$J (\ mathbf {w}) = \ sigma ^ 2_d - \ mathbf {w} ^ H \ mathbf {p} - \ mathbf {p} ^ H \ mathbf {w} + \ mathbf {w} ^ H \ mathbf { R} \ mathbf {w} \ qquad (3)$

onde $\ sigma ^ 2_d$ É a variação do sinal esperado, $\ mathbf {p} = E \ {\ mathbf {u} (n) d ^ * (n) \}$ É o vetor de correlação cruzada entre o vetor de entrada e o sinal esperado e $\ mathbf {R} = E \ {\ mathbf {u} (n) \ mathbf {u} ^ H (n) \}$ É a matriz de autocorrelação do sinal de entrada.

A conclusão desta fórmula está aqui (tentei mais claramente).

Como observamos acima, se estamos falando de programação convexa, teremos um extremo (mínimo). Portanto, para encontrar o valor mínimo da função de custo (o erro mínimo quadrático médio da raiz), basta encontrar a tangente da inclinação da tangente ou, em outras palavras, a derivada parcial em relação à nossa variável estudada:

$\ frac {\ delta J (\ mathbf {w})} {\ delta w ^ *} = - \ mathbf {p} + \ mathbf {R} \ mathbf {w} \ qquad (4)$

Na melhor das hipóteses ( $\ mathbf {w} = \ mathbf {w} _ {opt}$ ), é claro que o erro deve ser mínimo, o que significa que equiparamos a derivada a zero:

$\ mathbf {R} \ mathbf {w} _ {opt} = \ mathbf {p} \ qquad (5)$

Na verdade, aqui está, nosso fogão, do qual dançaremos mais adiante: diante de nós existe um sistema de equações lineares .

Como vamos decidir?

Deve-se notar imediatamente que ambas as soluções, que consideraremos a seguir, neste caso são teóricas e educacionais, pois $\ mathbf {R}$ e $\ mathbf {p}$ conhecido antecipadamente (ou seja, tínhamos a capacidade suposta de coletar estatísticas suficientes para calculá-las). No entanto, a análise de exemplos simplificados aqui é a melhor que você pode pensar para entender as abordagens básicas.

Solução analítica

Este problema pode ser resolvido, por assim dizer, na testa - usando matrizes inversas:

$\ mathbf {w} _ {opt} = \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (6)$

Essa expressão é chamada de equação de Wiener - Hopf - ainda é útil para nós como referência.

Obviamente, para ser completamente meticuloso, provavelmente seria mais correto escrever esse caso de uma maneira geral, ou seja, não com $^ {-}$ e com ( pseudo invertido ):
$\ mathbf {R} ^ + = \ mathbf {R} ^ H (\ mathbf {R} \ mathbf {R} ^ H) ^ {- 1}$

No entanto, a matriz de autocorrelação não pode ser não quadrada ou singular; portanto, com razão, acreditamos que não há contradição.

A partir desta equação, é analiticamente possível deduzir qual será o valor mínimo da função de custo (ou seja, no nosso caso, MEEM - erro médio quadrático médio):

$J_ {min} = J (\ mathbf {w} _ {opt}) = \ sigma ^ 2_d - \ mathbf {p} ^ H \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (7)$

A derivação da fórmula está aqui (também tentei torná-la mais colorida).

Bem, há uma solução.

Solução iterativa

No entanto, sim, é possível resolver um sistema de equações lineares sem inverter a matriz de autocorrelação - iterativamente ( para salvar cálculos ). Para esse fim, considere o método nativo e compreensível de descida de gradiente ( método de descida mais íngreme / gradiente ).

A essência do algoritmo pode ser reduzida para o seguinte:

Definimos a variável desejada para algum valor padrão (por exemplo, $\ mathbf {w} (0) = \ mathbf {0}$ )
Escolha algum passo $\ mu$ (como exatamente escolhemos, falaremos abaixo).
E então, por assim dizer, descemos ao longo de nossa superfície original (no nosso caso, essa é a superfície MSE) com uma determinada etapa $\ mu$ e uma certa velocidade determinada pela magnitude do gradiente.

Daí o nome: gradiente - gradiente ou mais íngreme - descida passo a passo - descida.

O gradiente em nosso caso já é conhecido: de fato, o encontramos quando diferenciamos a função de custo (a superfície é côncava, compare com [1, p. 220]). Escrevemos como será a fórmula para atualização iterativa da variável desejada (coeficientes de filtro) [1, p. 220]:

$\ mathbf {w} (n + 1) = \ mathbf {w} (n) - \ mu [- \ mathbf {p} + \ mathbf {R} \ mathbf {w} (n)] \ qquad (8)$

onde É o número da iteração.

Agora vamos falar sobre a escolha de um tamanho de etapa.

Listamos as premissas óbvias:

o passo não pode ser negativo ou zero
o passo não deve ser muito grande, caso contrário, o algoritmo não convergirá (por assim dizer, pulará de ponta a ponta, sem cair no extremo)
a etapa, é claro, pode ser muito pequena, mas isso também não é totalmente desejável - o algoritmo passará mais tempo

Com relação ao filtro Wiener, é claro que restrições já foram encontradas há muito tempo [1, p. 222-226]:

$0 <\ mu <\ frac {2} {\ lambda_ {max}} \ qquad (9)$

onde $\ lambda_ {max}$ É o maior autovalor da matriz de autocorrelação $\ mathbf {R}$ .

A propósito, autovalores e vetores são um tópico interessante separado no contexto da filtragem linear. Existe até um filtro Eigen completo para este caso (consulte o Apêndice 1).

Mas isso, felizmente, não é tudo. Há também uma solução ideal e adaptável:

$\ mu (n) = \ frac {\ mathbf {\ gamma} (n) ^ H \ mathbf {\ gamma} (n)} {\ mathbf {\ gamma} (n) ^ H \ mathbf {R} \ mathbf { \ gama} (n)} \ qquad (10)$

onde $\ mathbf {\ gama} (n) = \ mathbf {p} - \ mathbf {R} \ mathbf {w} (n)$ É um gradiente negativo. Como pode ser visto na fórmula, a etapa é recalculada em cada iteração, ou seja, se adapta.

A conclusão da fórmula está aqui (muita matemática - olhe apenas para os mesmos nerds notórios como eu).

Ok, para a segunda decisão, também montamos o palco.

Mas é possível com exemplos?

Por uma questão de clareza, realizaremos uma pequena simulação. Usaremos o Python 3.6.4 .

Eu direi imediatamente que esses exemplos fazem parte de um dos trabalhos de casa, cada um dos quais é oferecido aos alunos para solução dentro de duas semanas. Reescrevi a parte em python (para popularizar a linguagem entre os engenheiros de rádio). Talvez você encontre outras opções na Web de outros ex-alunos.

import numpy as np import matplotlib.pyplot as plt from scipy.linalg import toeplitz def convmtx(h,n): return toeplitz(np.hstack([h, np.zeros(n-1)]),\ np.hstack([h[0], np.zeros(n-1)])) def MSE_calc(sigmaS, R, p, w): w = w.reshape(w.shape[0], 1) wH = np.conj(w).reshape(1, w.shape[0]) p = p.reshape(p.shape[0], 1) pH = np.conj(p).reshape(1, p.shape[0]) MSE = sigmaS - np.dot(wH, p) - np.dot(pH, w) + np.dot(np.dot(wH, R), w) return MSE[0, 0] def mu_opt_calc(gamma, R): gamma = gamma.reshape(gamma.shape[0], 1) gammaH = np.conj(gamma).reshape(1, gamma.shape[0]) mu_opt = np.dot(gammaH, gamma) / np.dot(np.dot(gammaH, R), gamma) return mu_opt[0, 0]

Usaremos nosso filtro linear para o problema de equalização do canal , cujo principal objetivo é nivelar os vários efeitos desse canal no sinal útil.

O código fonte pode ser baixado em um arquivo aqui ou aqui (sim, eu tive um hobby - editar Wikipedia).

Modelo do sistema

Suponha que exista um conjunto de antenas (já o examinamos em um artigo sobre MUSIC ).

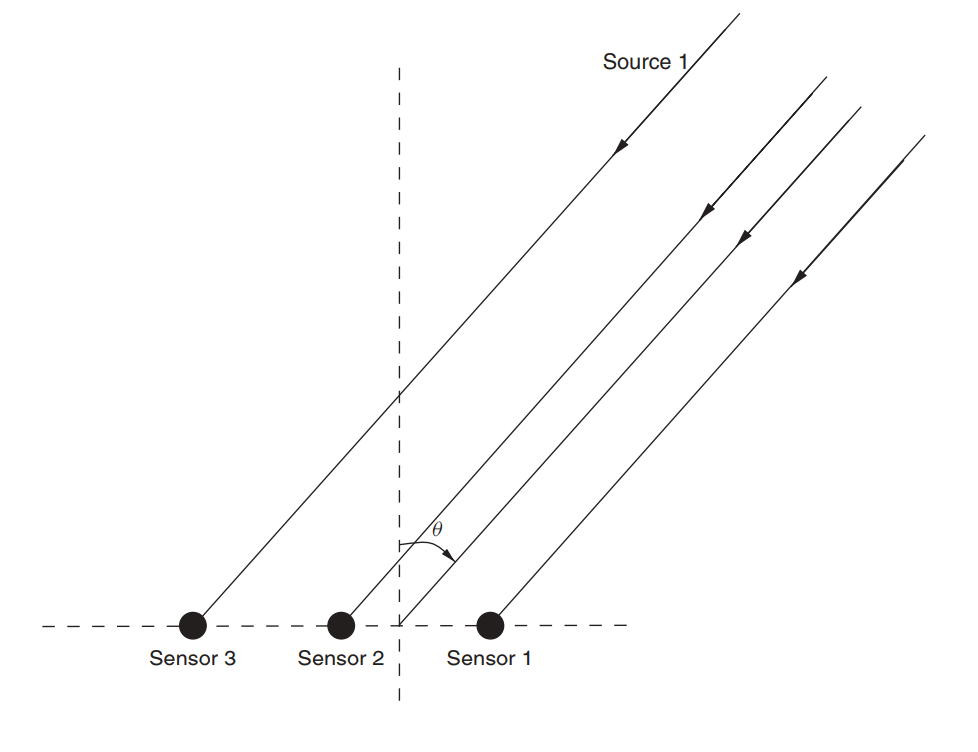
Fig. 3. Conjunto de antenas lineares não direcionais (ULAA - conjunto de antenas lineares uniformes) [2, p. 32]

Defina os parâmetros iniciais da estrutura:

 M = 5 #    (number of sensors)

Neste artigo, consideraremos algo como um canal de banda larga com desbotamento , um recurso característico da propagação de caminhos múltiplos . Para tais casos, geralmente é aplicada uma abordagem na qual cada feixe é modelado usando um atraso de uma certa magnitude (Fig. 4).

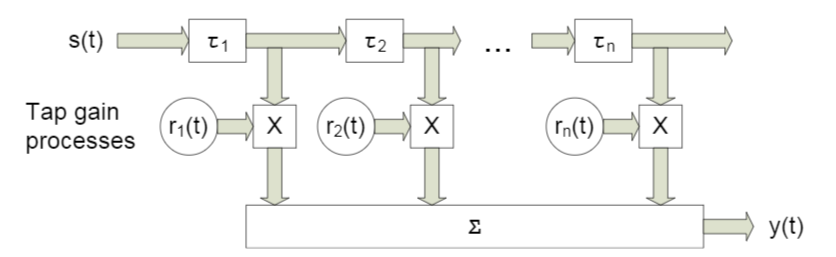
Fig. 4. O modelo do canal de banda larga com n atrasos fixos. [3, p. 29] Como você entende, designações específicas não desempenham um papel - a seguir, usaremos designações ligeiramente diferentes.

O modelo do sinal recebido para um sensor é expresso da seguinte forma:

$x (n) = \ sum_ {l = 0} ^ Lh (l) s (n-l) + \ nu (n)$

Neste caso indica o número de referência, h (l) É a resposta do canal ao longo do l- ésimo feixe, L é o número de registros de atraso, s é o sinal transmitido (útil), $\ nu (n)$ - ruído aditivo.

Para vários sensores, a fórmula assumirá a forma:

$\ mathbf {x} (n) = \ mathbf {H} \ mathbf {s} (n) + \ mathbf {\ nu} (n)$

onde $\ mathbf {x} (n)$ e $\ mathbf {\ nu} (n)$ - ter dimensão $M \ times 1$ dimensão $\ mathbf {H}$ é igual a $M \ vezes (M-L)$ e a dimensão $\ mathbf {s} (n)$ é igual a $(M-L) \ vezes 1$ .

Suponha que cada sensor também receba um sinal com um certo atraso, devido à incidência da onda em um ângulo. Matrix $\ mathbf {H}$ no nosso caso, será uma matriz convolucional para o vetor de resposta para cada raio. Eu acho que o código será mais claro:

 h = np.array([0.722-1j*0.779, -0.257-1j*0.722, -0.789-1j*1.862]) L = len(h)-1 # number of signal sources H = convmtx(h,ML) print(H.shape) print(H)

A conclusão será:

 >>> (5, 3) >>> array([[ 0.722-0.779j, 0. +0.j , 0. +0.j ], [-0.257-0.722j, 0.722-0.779j, 0. +0.j ], [-0.789-1.862j, -0.257-0.722j, 0.722-0.779j], [ 0. +0.j , -0.789-1.862j, -0.257-0.722j], [ 0. +0.j , 0. +0.j , -0.789-1.862j]])

Em seguida, definimos os dados iniciais para o sinal e ruído úteis:

 sigmaS = 1 #    (the signal's s(n) power) sigmaN = 0.01 #   (the noise's n(n) power)

Agora passamos a correlações.

 Rxx = (sigmaS)*(np.dot(H,np.matrix(H).H))+(sigmaN)*np.identity(M) p = (sigmaS)*H[:,0] p = p.reshape((len(p), 1))

A derivação das fórmulas aqui (também uma folha para os mais desesperados).

Encontramos uma solução para o Wiener:

 # Solution of the Wiener-Hopf equation: wopt = np.dot(np.linalg.inv(Rxx), p) MSEopt = MSE_calc(sigmaS, Rxx, p, wopt)

Agora vamos para o método de descida de gradiente.

Encontre o maior valor próprio para que dele possa ser derivado o limite superior da etapa (consulte a fórmula (9)):

 lamda_max = max(np.linalg.eigvals(Rxx))

Agora vamos definir uma série de etapas que formarão uma certa fração do máximo:

 coeff = np.array([1, 0.9, 0.5, 0.2, 0.1]) mus = 2/lamda_max*coeff # different step sizes

Defina o número máximo de iterações:

 N_steps = 100

Execute o algoritmo:

 MSE = np.empty((len(mus), N_steps), dtype=complex) for mu_idx, mu in enumerate(mus): w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): w = w - mu*(np.dot(Rxx, w) - p) MSE[mu_idx, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Agora faremos o mesmo, mas para a etapa adaptativa (fórmula (10)):

 MSEoptmu = np.empty((1, N_steps), dtype=complex) w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): gamma = p - np.dot(Rxx,w) mu_opt = mu_opt_calc(gamma, Rxx) w = w - mu_opt*(np.dot(Rxx,w) - p) MSEoptmu[:, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Você deve obter algo como isto:

Desenhando

 x = [i for i in range(1, N_steps+1)] plt.figure(figsize=(5, 4), dpi=300) for idx, item in enumerate(coeff): if item == 1: item = '' plt.loglog(x, np.abs(MSE[idx, :]),\ label='$\mu = '+str(item)+'\mu_{max}$') plt.loglog(x, np.abs(MSEoptmu[0, :]),\ label='$\mu = \mu_{opt}$') plt.loglog(x, np.abs(MSEopt*np.ones((len(x), 1), dtype=complex)),\ label = 'Wiener solution') plt.grid(True) plt.xlabel('Number of steps') plt.ylabel('Mean-Square Error') plt.title('Steepest descent') plt.legend(loc='best') plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

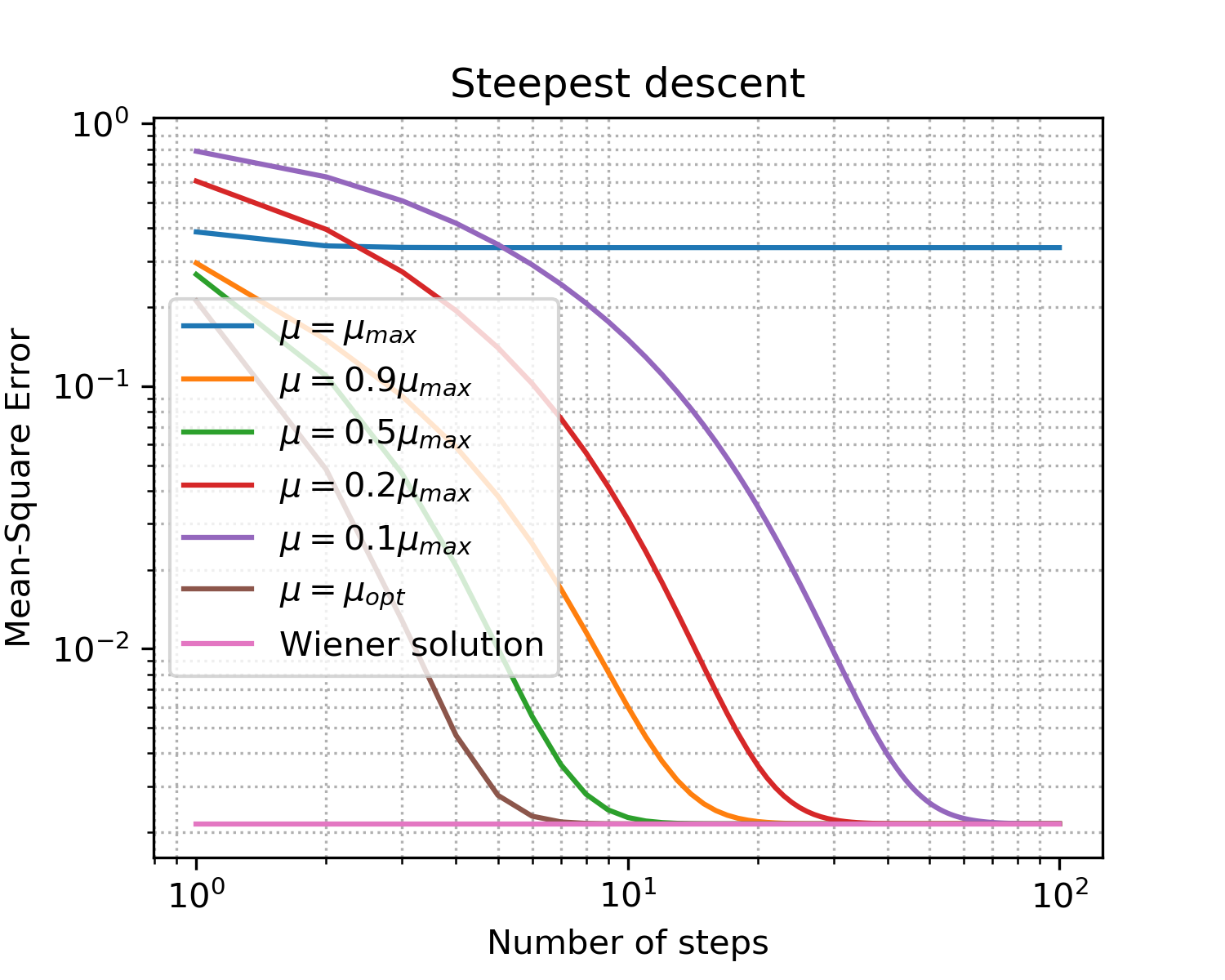
Fig. 5. Curvas de aprendizado para etapas de tamanhos diferentes.

Fixações com o objetivo de falar os principais pontos da descida do gradiente:

como esperado, o passo ideal fornece a convergência mais rápida;
não significa mais melhor: tendo excedido o limite superior, não alcançamos convergência.

Então encontramos o vetor ideal de coeficientes de filtro que melhor nivelará os efeitos do canal - treinamos o equalizador .

Existe algo mais próximo da realidade?

Claro! Já dissemos várias vezes que a coleta de estatísticas (isto é, cálculo de matrizes e vetores de correlação) em sistemas em tempo real está longe de ser sempre um luxo acessível. No entanto, a humanidade se adaptou a essas dificuldades: em vez de uma abordagem determinista na prática, abordagens adaptativas são usadas. Eles podem ser divididos em dois grandes grupos [1, p. 246]:

probabilístico (estocástico) (por exemplo, SG - gradiente estocástico)
e com base no método dos mínimos quadrados (por exemplo, LMS - Mínimos quadrados médios ou RLS - Mínimos quadrados recursivos)

O tópico de filtros adaptativos está bem representado na comunidade de código aberto (exemplos para python):

No segundo exemplo, gosto especialmente da documentação. No entanto, tenha cuidado! Quando testei o pacote padasip , tive dificuldades em lidar com números complexos (por padrão, float64 está implícito). Talvez os mesmos problemas possam surgir ao trabalhar com outras implementações.

Os algoritmos, é claro, têm suas próprias vantagens e desvantagens, cuja soma determina o escopo do algoritmo.

Vamos dar uma rápida olhada nos exemplos: consideraremos os três algoritmos SG , LMS e RLS que já mencionamos (modelaremos na linguagem MATLAB - confesso, já havia espaços em branco e reescreveremos tudo para uniformizar o python por uma questão de ... bem ...).

Uma descrição dos algoritmos LMS e RLS pode ser encontrada, por exemplo, na doca padasip .

A descrição do SG pode ser encontrada aqui.

A principal diferença da descida do gradiente é um gradiente variável:

$\ mathbf {w} [n] = \ mathbf {w} [n-1] + \ mu \ left (\ mathbf {\ hat {p}} [n] - \ mathbf {\ hat {R}} _ {xx } [n] \ mathbf {w} [n-1] \ right)$

às

$\ mathbf {\ hat {R}} _ {xx} [n] = \ frac {1} {n} \ esquerda ((n-1) \ mathbf {\ hat {R}} _ {xx} [n-1 ] + \ mathbf {x} [n] \ mathbf {x} [n] ^ H \ à direita)$

$\ mathbf {\ hat {p}} [n] = \ frac {1} {n} \ left ((n-1) \ mathbf {\ hat {p}} [n-1] + \ mathbf {x} [ n] d [n] ^ * \ right)$

1) Um caso semelhante ao considerado acima.

Fontes (MatLab / Octave).

As fontes podem ser baixadas aqui .

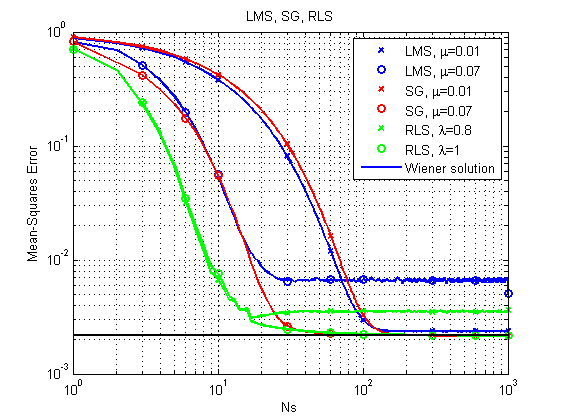
Fig. 6. Curvas de aprendizado para LMS, RLS e SG.

Pode-se notar imediatamente que, com sua relativa simplicidade, o algoritmo LMS pode, em princípio, não chegar a uma solução ótima com um passo relativamente grande. O RLS fornece o resultado mais rápido, mas também pode falhar com um fator de esquecimento relativamente pequeno. Até agora, a SG está indo bem, mas vamos ver outro exemplo.

2) O caso em que o canal muda com o tempo.

Fontes (MatLab / Octave).

As fontes podem ser baixadas aqui .

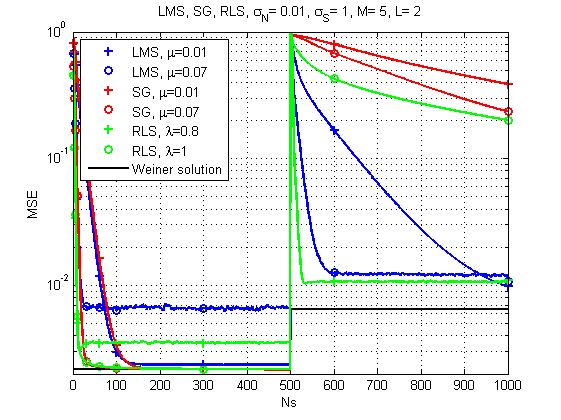
Fig. 7. Curvas de aprendizado para LMS, RLS e SG (mudanças de canal ao longo do tempo).

E aqui a imagem já é muito mais interessante: com uma mudança acentuada na resposta do canal, o LMS já parece ser a solução mais confiável. Quem teria pensado. Embora o RLS com o fator de esquecimento certo também forneça um resultado aceitável.

Algumas palavras sobre desempenho.

Sim, é claro, cada algoritmo tem sua própria complexidade computacional específica, mas, de acordo com minhas medições, minha máquina antiga pode lidar com um conjunto por cerca de 120 μs por iteração no caso do LMS e SG e cerca de 250 μs por iteração no caso do RLS. Ou seja, a diferença é, em geral, comparável.

E isso é tudo por hoje. Obrigado a todos que olharam!

Literatura

Teoria do filtro adaptativo Haykin SS. - Pearson Education India, 2005.
Haykin, Simon e KJ Ray Liu. Manual sobre processamento de array e redes de sensores. Vol. 63. John Wiley & Sons, 2010. pp. 102-107
Arndt, D. (2015). Modelagem em canal para recepção de satélite móvel terrestre (dissertação de doutorado).

Apêndice 1

Filtro Eigen

O principal objetivo desse filtro é maximizar a relação sinal-ruído (SNR).

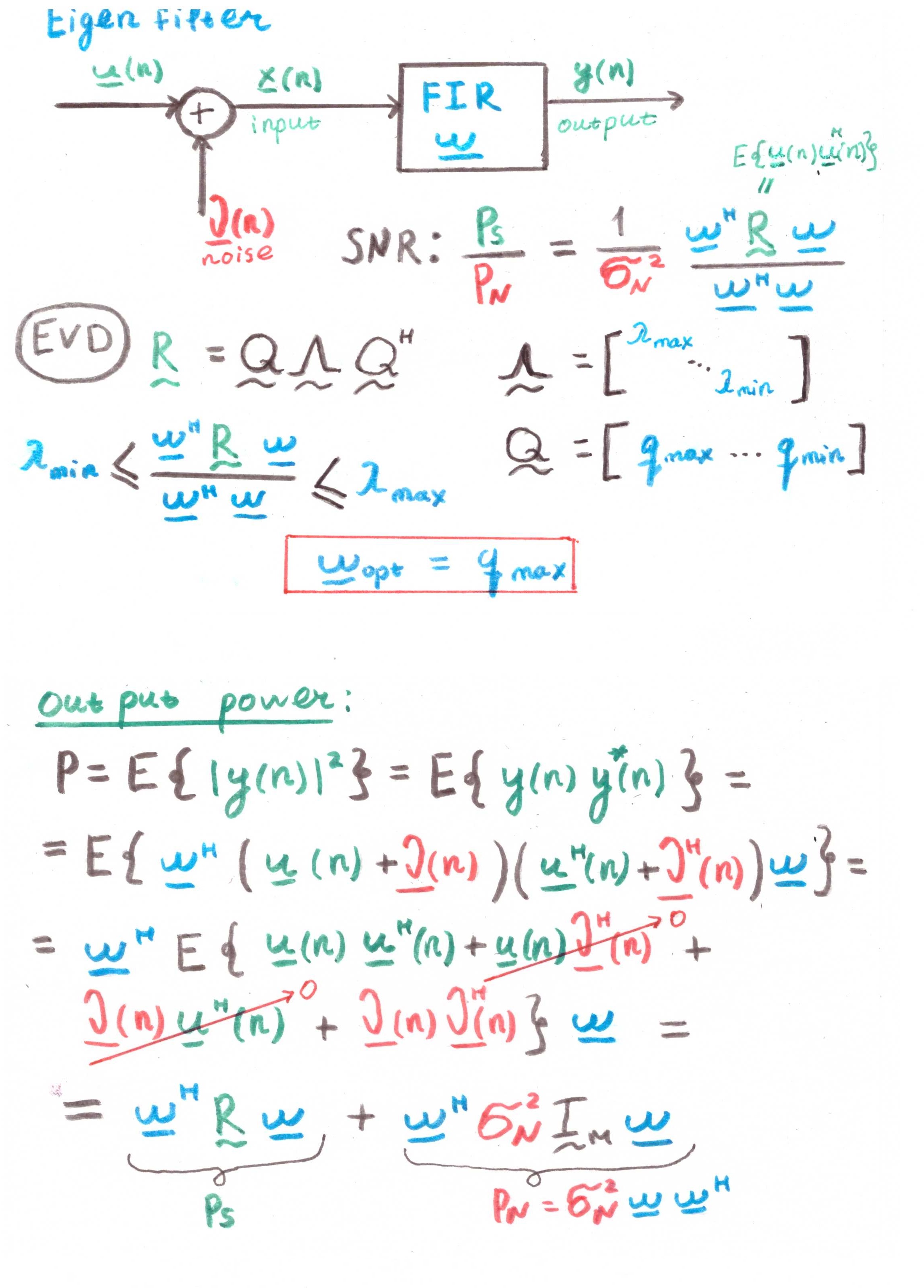
Mas, a julgar pela presença de correlações nos cálculos, isso também é mais um construto teórico do que uma solução prática.

Filtragem linear ideal: de descida gradiente a filtros adaptativos