Não é segredo que um dos passatempos favoritos de um desenvolvedor de software é entrevistar empregadores. Todos fazemos isso de tempos em tempos e por razões completamente diferentes. E o mais óbvio deles - a procura de emprego - acho que não é o mais comum. Participar de uma entrevista é uma boa maneira de manter a forma, repetir o básico esquecido e aprender algo novo. E se for bem-sucedido, também aumente a autoconfiança. Ficamos entediados, definimos o status de "aberto a ofertas" em algum tipo de rede social "comercial" como
"LinkedIn" - e o exército de gerentes de recursos humanos já está atacando nossas caixas de entrada para receber mensagens.

No processo, enquanto todo esse tumulto está acontecendo, somos confrontados com muitas perguntas que, como dizem do outro lado da cortina implícita, estão "tocando um sino", e seus detalhes estão ocultos por trás da
neblina da guerra . Na maioria das vezes, eles são lembrados apenas em testes por algoritmos e estruturas de dados (pessoalmente, eu não tinha esses dados) e, na verdade, entrevistas.
Uma das perguntas mais comuns em uma entrevista para um programador de qualquer especialização é a lista. Por exemplo, listas vinculadas individualmente. E algoritmos básicos relacionados. Por exemplo, uma inversão de marcha. E, geralmente, isso acontece da seguinte maneira: "Bom, mas como você expandiria uma lista vinculada individualmente?" O principal é pegar o candidato de surpresa com esta pergunta.
Na verdade, tudo isso me levou a escrever essa breve resenha para lembretes e edificações constantes. Então, brincadeiras à parte, eis!
Lista vinculada individualmente
Uma lista vinculada é uma das
estruturas básicas de
dados . Cada elemento (ou nó) consiste em, de fato, dados armazenados e links para elementos vizinhos. Uma lista vinculada individualmente armazena apenas um link para o próximo elemento na estrutura e uma lista
duplamente vinculada mantém o link para o próximo e o anterior. Essa organização dos dados permite que eles estejam localizados em qualquer área da memória (diferente de, por exemplo, uma
matriz , cujos elementos devem estar localizados na memória, um após o outro).
Há muito mais a ser dito sobre listas, é claro: elas podem ser circulares (ou seja, o último elemento armazena um link para o primeiro) ou não (ou seja, não há link para o último elemento). As listas podem ser digitadas, ou seja, contém dados do mesmo tipo ou não. E assim por diante e assim por diante.
Melhor tentar escrever algum código. Por exemplo, de alguma forma, você pode imaginar um nó da lista:
final class Node<T> { let payload: T var nextNode: Node? init(payload: T, nextNode: Node? = nil) { self.payload = payload self.nextNode = nextNode } }
"Genérico" é um tipo capaz de armazenar cargas úteis de qualquer tipo no campo de
payload .
A lista em si é exaustivamente identificada por seu primeiro nó:
final class SinglyLinkedList<T> { var firstNode: Node<T>? init(firstNode: Node<T>? = nil) { self.firstNode = firstNode } }
O primeiro nó é declarado opcional, porque a lista pode estar vazia.
Em teoria, é claro, na classe você precisa implementar todos os métodos necessários - inserir, excluir, acessar nós, etc., mas faremos isso em outro momento. Ao mesmo tempo, verificaremos se o uso de struct (com o qual a Apple nos incentiva ativamente pelo nosso exemplo) é uma escolha melhor e talvez lembremos a abordagem "Copiar na gravação" .Propagação de lista vinculada única
O primeiro caminho. Ciclo
Chegou a hora de começarmos os negócios para os quais estamos aqui hoje! E a maneira mais eficaz de lidar com isso é de duas maneiras. O primeiro é um loop simples, do primeiro ao último nó.
O ciclo trabalha com três variáveis, que antes do início recebem o valor do nó anterior, atual e seguinte. (Nesse momento, o valor do nó anterior está naturalmente vazio.) O ciclo começa verificando se o próximo nó não está vazio e, nesse caso, o corpo do ciclo é executado. Nenhuma mágica acontece no loop: no nó atual, o campo que se refere ao próximo elemento recebe um link para o anterior (na primeira iteração, o valor do link, respectivamente, é redefinido, o que corresponde ao estado de coisas no último nó). Além disso, as variáveis correspondentes ao nó anterior, atual e seguinte recebem novos valores. Após sair do loop, o nó atual (ou seja, o último iterável em geral) recebe um novo valor de link para o próximo nó, porque A saída do loop ocorre exatamente no momento em que o último nó da lista se torna atual.
Em palavras, é claro, tudo isso parece estranho e incompreensível, então é melhor olhar para o código:
extension SinglyLinkedList { func reverse() { var previousNode: Node<T>? = nil var currentNode = firstNode var nextNode = firstNode?.nextNode while nextNode != nil { currentNode?.nextNode = previousNode previousNode = currentNode currentNode = nextNode nextNode = currentNode?.nextNode } currentNode?.nextNode = previousNode firstNode = currentNode } }
Para verificação, usamos uma lista de nós cujas cargas úteis são identificadores
inteiros simples. Crie uma lista de dez elementos:
let node = Node(payload: 0)
Tudo parece estar bem, mas somos pessoas, não computadores, e seria bom obter uma prova visual da exatidão da lista criada e do algoritmo descrito acima. Talvez uma simples impressão seja suficiente. Para tornar a saída legível, adicione a implementação do protocolo
CustomStringConvertible nó com um identificador inteiro:
extension Node: CustomStringConvertible where T == Int { var description: String { let firstPart = """ Node \(Unmanaged.passUnretained(self).toOpaque()) has id \(payload) and """ if let nextNode = nextNode { return firstPart + " next node \(nextNode.payload)." } else { return firstPart + " no next node." } } }
... E a lista correspondente para exibir todos os nós em ordem:
extension SinglyLinkedList: CustomStringConvertible where T == Int { var description: String { var description = """ List \(Unmanaged.passUnretained(self).toOpaque()) """ if firstNode != nil { description += " has nodes:\n" var node = firstNode while node != nil { description += (node!.description + "\n") node = node!.nextNode } return description } else { return description + " has no nodes." } } }
A representação de string de nossos tipos conterá um endereço na memória e um identificador inteiro. Utilizando-os, organizamos a impressão da lista gerada de dez nós:
print(String(describing: list))
Expanda esta lista e imprima-a novamente:
list.reverse() print(String(describing: list))
Você pode observar que os endereços na memória da lista e dos nós não foram alterados e os nós da lista são impressos na ordem inversa. As referências ao próximo elemento do nó agora apontam para o anterior (isto é, por exemplo, o próximo elemento do nó “5” agora não é “6”, mas “4”). E isso significa que conseguimos!
O segundo caminho. Recursão
A segunda maneira conhecida de fazer a mesma inversão de marcha é baseada na
recursão . Para implementá-lo, declararemos uma função que pega o primeiro nó da lista e retorna o primeiro nó "novo" (que era o último antes).
O parâmetro e o valor de retorno são opcionais, porque, dentro dessa função, é chamado repetidamente em cada nó subsequente até ficar vazio (ou seja, até o final da lista). Portanto, no corpo da função, é necessário verificar se o nó no qual a função é chamada está vazio e se esse nó possui o seguinte. Caso contrário, a função retornará o que foi passado para o argumento.
Na verdade, tentei honestamente descrever o algoritmo completo em palavras, mas no final apaguei quase tudo, porque o resultado seria impossível de entender. Para desenhar fluxogramas e descrever formalmente as etapas do algoritmo - também, neste caso, acho que não faz sentido, porque será mais conveniente para você e eu apenas lermos e tentarmos compreender o código
Swift :
extension SinglyLinkedList { func reverseRecursively() { func reverse(_ node: Node<T>?) -> Node<T>? { guard let head = node else { return node } if head.nextNode == nil { return head } let reversedHead = reverse(head.nextNode) head.nextNode?.nextNode = head head.nextNode = nil return reversedHead } firstNode = reverse(firstNode) } }
O próprio algoritmo é "encapsulado" por um método do próprio tipo de lista, para a conveniência de chamar.
Parece mais curto, mas, na minha opinião, mais difícil de entender.
Chamamos esse método no resultado do spread anterior e imprimimos um novo resultado:
list.reverseRecursively() print(String(describing: list))
Pode-se ver pela saída que todos os endereços na memória não foram alterados novamente e os nós agora seguem na ordem original (ou seja, eles são "implantados" novamente). E isso significa que acertamos novamente!
Conclusões
Se você observar cuidadosamente os métodos de reversão (ou realizar um experimento com contagem de chamadas), notará que o loop no primeiro caso e a chamada interna (recursiva) no segundo caso ocorrem uma vez menos que o número de nós na lista (no nosso caso, nove vezes). Você também pode prestar atenção ao que acontece ao redor do loop no primeiro caso - a mesma sequência de atribuições - e à primeira chamada de método não recursiva no segundo caso. Acontece que em ambos os casos o "círculo" é repetido exatamente dez vezes para uma lista de dez nós. Assim, temos
complexidade linear para ambos os algoritmos -
O (n) .
De um modo geral, os dois algoritmos descritos são considerados os mais eficazes para resolver esse problema. Quanto à complexidade computacional, não é possível criar um algoritmo com um valor mais baixo: de uma forma ou de outra, é necessário "visitar" cada nó para atribuir um novo valor ao que está armazenado no link.
Outro recurso que vale a pena mencionar é a "complexidade da memória alocada". Ambos os algoritmos propostos criam um número fixo de novas variáveis (três no primeiro caso e uma no segundo). Isso significa que a quantidade de memória alocada não depende das características quantitativas dos dados de entrada e é descrita por uma função constante - O (1).
Mas, de fato, no segundo caso, não é assim. O perigo de recursão é que memória extra é alocada para cada chamada recursiva na
pilha . No nosso caso, a profundidade da recursão corresponde à quantidade de dados de entrada.
E finalmente, decidi experimentar um pouco mais: de maneira simples e primitiva, medi o tempo de execução absoluto de dois métodos para uma quantidade diferente de dados de entrada. Assim:
let startDate = Date().timeIntervalSince1970
E é isso que eu recebi (esses são os dados brutos do
Playground ):
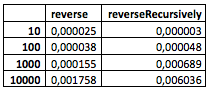
(Infelizmente, meu computador não domina os valores maiores.)
O que pode ser visto da mesa? Nada de especial ainda. Embora já seja perceptível que o método recursivo se comporte um pouco pior com um número relativamente pequeno de nós, mas em algum lugar entre 100 e 1000, ele começa a mostrar melhor.
Eu também tentei o mesmo teste simples em um projeto
"Xcode" completo. Os resultados são os seguintes:

Em primeiro lugar, vale ressaltar que os resultados foram obtidos após a ativação do modo de otimização “agressivo” visando a velocidade de execução (
-Ofast ), razão pela qual em parte os números são tão pequenos. Também é interessante que, neste caso, o método recursivo tenha se mostrado um pouco melhor, pelo contrário, apenas em tamanhos muito pequenos de dados de entrada, e já em uma lista de 100 nós, o método perde. Dos 100.000, ele fez o programa terminar de forma anormal.
Conclusão
Tentei abordar um tópico bastante clássico do ponto de vista da minha linguagem de programação favorita no momento, e espero que você tenha curiosidade em acompanhar o progresso, assim como eu. Também fico muito feliz se você conseguiu aprender algo novo - então definitivamente perdi meu tempo neste artigo (em vez de sentar e assistir a
programas de TV ).
Se alguém deseja acompanhar minha atividade social, aqui está um link para o meu “Twitter” , onde, antes de tudo, há links para minhas novas postagens e um pouco mais.