Se o artigo anterior teve maior probabilidade de ser propagado, agora é hora de testar os recursos de paralelização de Julia em sua máquina.
Processamento multinúcleo ou distribuído
A implementação da computação paralela com memória distribuída é fornecida pelo módulo Distributed como parte da biblioteca padrão fornecida com a Julia. A maioria dos computadores modernos possui mais de um processador e vários computadores podem ser agrupados em cluster. Usar o poder desses múltiplos processadores permite realizar muitos cálculos mais rapidamente. O desempenho é afetado por dois fatores principais: a velocidade dos próprios processadores e a velocidade do acesso à memória. No cluster, é óbvio que esta CPU terá o acesso mais rápido à RAM no mesmo computador (nó). Talvez ainda mais surpreendente, esses problemas sejam relevantes em um laptop típico com vários núcleos devido a diferenças na velocidade da memória principal e do cache. Portanto, um bom ambiente multiprocessador deve permitir que você controle a "propriedade" de uma parte da memória por um processador específico. Julia fornece um ambiente multiprocessador baseado em mensagens que permite que os programas sejam executados simultaneamente em vários processos em diferentes domínios de memória.
A implementação de mensagens de Julia é diferente de outros ambientes, como o MPI [1] . A comunicação em Julia é geralmente "unidirecional", o que significa que o programador precisa controlar explicitamente apenas um processo em uma operação de dois processos. Além disso, essas operações geralmente não se parecem com "enviar uma mensagem" e "receber uma mensagem", mas sim com operações de nível superior, como chamadas para funções definidas pelo usuário.
A programação distribuída em Julia se baseia em duas primitivas: links remotos e chamadas remotas . Um link remoto é um objeto que pode ser usado em qualquer processo para se referir a um objeto armazenado em um processo específico. Uma chamada remota é uma solicitação de um processo para chamar uma determinada função de acordo com certos argumentos de outro processo (possivelmente o mesmo).
Os links remotos têm duas formas: Future e RemoteChannel .
Uma chamada remota retorna Future e faz isso imediatamente; o processo que fez a chamada prossegue para a próxima operação, enquanto a chamada remota ocorre em outro lugar. Você pode aguardar a conclusão da chamada remota com o comando de espera para o Future retornado e também pode obter o valor total do resultado usando a busca .
Por outro lado, temos RemoteChannels que são reescritos. Por exemplo, vários processos podem coordenar seu processamento, referindo-se ao mesmo canal remoto. Cada processo tem um identificador associado. O processo que fornece o prompt interativo Julia sempre tem um identificador de 1. Os processos usados por padrão para operações simultâneas são chamados de "trabalhadores". Quando há apenas um processo, o processo 1 é considerado funcionando. Caso contrário, todos os processos que não sejam o processo 1 são considerados trabalhadores.

Vamos ao que interessa. julia -pn com julia -pn postscript fornece n fluxos de trabalho no computador local. Geralmente, faz sentido que n seja igual ao número de threads da CPU (núcleos lógicos) na máquina. Observe que o argumento -p carrega implicitamente o módulo Distributed.
Como iniciar um postscript?As operações do console devem ser diretas para usuários do Linux, incl. Este programa educacional é destinado a usuários inexperientes do Windows.
O Terminal Julia (REPL) fornece a capacidade de usar comandos do sistema:
julia> pwd() # "C:\\Users\\User\\AppData\\Local\\Julia-1.1.0" julia> cd("C:/Users/User/Desktop") # julia> run(`calc`) # # Windows. # Process(`calc`, ProcessExited(0))
usando esses comandos, você pode iniciar Julia a partir de Julia, mas é melhor não se deixar levar
Seria mais correto executar o cmd a partir de julia / bin / e executar o comando julia -p 2 lá ou uma opção para os amantes de iniciar a partir de um atalho: na área de trabalho, crie um documento no bloco de notas com o seguinte conteúdo C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 ( especifique o endereço e o número de processos ) e salve-o como um documento de texto com o nome run.bat . Aqui, agora na área de trabalho, há um arquivo de sistema de inicialização Julia para 4 núcleos.
Você pode usar outro método (especialmente relevante para o Jupyter ):
using Distributed addprocs(2)
$ ./julia -p 2 julia> r = remotecall(rand, 2, 2, 2) Future(2, 1, 4, nothing) julia> s = @spawnat 2 1 .+ fetch(r) Future(2, 1, 5, nothing) julia> fetch(s) 2×2 Array{Float64,2}: 1.18526 1.50912 1.16296 1.60607
O primeiro argumento a chamar novamente é a função chamada.
A maioria dos programas concorrentes em Julia não se refere a processos específicos ou ao número de processos disponíveis, mas uma chamada remota é considerada uma interface de baixo nível que fornece controle mais preciso.
O segundo argumento para remotecall é o identificador do processo que fará o trabalho, e os argumentos restantes serão passados para a função chamada. Como você pode ver, na primeira linha, pedimos ao processo 2 para criar uma matriz aleatória 2 por 2, e na segunda linha, pedimos para adicionar 1 a ela. O resultado de ambos os cálculos está disponível em dois futuros, re s. A macro spawnat avalia a expressão no segundo argumento para o processo especificado no primeiro argumento. Às vezes, você pode precisar de um valor calculado remotamente. Isso geralmente acontece quando você lê de um objeto remoto para obter os dados necessários para a próxima operação local. Existe uma função remotecall_fetch para remotecall_fetch . Isso é equivalente a fetch (remotecall (...)) , mas é mais eficiente.
Lembre-se de que getindex(r, 1,1) equivalente a r[1,1] , portanto, essa chamada recupera o primeiro elemento do futuro r .
A remotecall chamada remota de chamada remota não remotecall particularmente conveniente. A macro @spawn facilita as @spawn . Ele funciona com uma expressão, não uma função e escolhe onde executar a operação para você:
julia> r = @spawn rand(2,2) Future(2, 1, 4, nothing) julia> s = @spawn 1 .+ fetch(r) Future(3, 1, 5, nothing) julia> fetch(s) 2×2 Array{Float64,2}: 1.38854 1.9098 1.20939 1.57158
Observe que usamos 1 .+ Fetch(r) vez de 1 .+ r Isso ocorre porque não sabemos onde o código será executado; portanto, no caso geral, pode ser necessário buscar para mover r para o processo de adição. Nesse caso, @spawn é inteligente o suficiente para executar cálculos para o processo que possui r , portanto, a busca não será operacional (nenhum trabalho é feito). (Vale a pena notar que a desova não é incorporada, mas definida em Julia como uma macro. Você pode definir suas próprias construções.)
É importante lembrar que, após a extração, o Future armazenará seu valor em cache localmente. Chamadas adicionais para buscar não implicam um salto na rede. Após a seleção de todos os futuros referentes, o valor armazenado excluído é excluído.
O @async é semelhante ao @spawn , mas executa tarefas apenas no processo local. Nós o usamos para criar uma tarefa de "feed" para cada processo. Cada tarefa seleciona o próximo índice, que deve ser calculado, aguarda a conclusão do processo e se repete até ficar sem índices.
Observe que as tarefas do alimentador não começam a ser executadas até que a tarefa principal chegue ao final do bloco @sync , após o que passa o controle e aguarda a conclusão de todas as tarefas locais antes de retornar da função.
Quanto à v0.7 e superior, as tarefas do alimentador podem compartilhar o estado através do nextidx, porque todas são executadas no mesmo processo. Mesmo que as tarefas sejam planejadas juntas, o bloqueio pode ser necessário em alguns contextos, como na E / S assíncrona. Isso significa que a alternância de contexto ocorre apenas em pontos bem definidos: nesse caso, quando remotecall_fetch é remotecall_fetch . Esse é o estado atual da implementação e pode ser alterado nas versões futuras do Julia, pois foi projetado para ser capaz de concluir até N tarefas em processos M ou M: N Threading . Em seguida, precisamos de um modelo para obter / liberar bloqueios para o nextidx , pois não é seguro permitir que vários processos leiam e gravem recursos ao mesmo tempo.
Seu código deve estar disponível para qualquer processo que o execute. Por exemplo, no prompt de Julia, digite o seguinte:
julia> function rand2(dims...) return 2*rand(dims...) end julia> rand2(2,2) 2×2 Array{Float64,2}: 0.153756 0.368514 1.15119 0.918912 julia> fetch(@spawn rand2(2,2)) ERROR: RemoteException(2, CapturedException(UndefVarError(Symbol("#rand2")) Stacktrace: [...]
O processo 1 sabia da função rand2, mas o processo 2 não. Na maioria das vezes, você baixa o código de arquivos ou pacotes e possui uma flexibilidade significativa no controle de quais processos carregam o código. Considere o arquivo DummyModule.jl que contém o seguinte código:
module DummyModule export MyType, f mutable struct MyType a::Int end f(x) = x^2+1 println("loaded") end
Para fazer referência ao MyType em todos os processos, o DummyModule.jl deve ser carregado em cada processo. Uma chamada para include ('DummyModule.jl') carrega apenas para um processo. Para carregá-lo em cada processo, use a macro @everywhere (execute Julia com julia -p 2):
julia> @everywhere include("DummyModule.jl") loaded From worker 3: loaded From worker 2: loaded
Como de costume, isso não torna o DummyModule acessível a qualquer processo que exija uso ou importação. Além disso, quando um DummyModule é incluído no escopo de um processo, ele não é incluído em nenhum outro:
julia> using .DummyModule julia> MyType(7) MyType(7) julia> fetch(@spawnat 2 MyType(7)) ERROR: On worker 2: UndefVarError: MyType not defined ⋮ julia> fetch(@spawnat 2 DummyModule.MyType(7)) MyType(7)
No entanto, ainda é possível, por exemplo, enviar MyType para o processo que carregou o DummyModule, mesmo que não esteja no escopo:
julia> put!(RemoteChannel(2), MyType(7)) RemoteChannel{Channel{Any}}(2, 1, 13)
O arquivo também pode ser pré-carregado em vários processos na inicialização com o sinalizador -L, e o script do driver pode ser usado para controlar os cálculos:
julia -p <n> -L file1.jl -L file2.jl driver.jl
O processo Julia que executa o script do driver no exemplo acima tem um identificador 1, assim como o processo que fornece o prompt interativo. Por fim, se DummyModule.jl não for um arquivo separado, mas um pacote, o uso do DummyModule carregará o DummyModule.jl em todos os processos, mas somente o transferirá para o escopo do processo para o qual o uso foi chamado.
Iniciando e gerenciando fluxos de trabalho
A instalação básica do Julia possui suporte interno para dois tipos de clusters:
- O cluster local especificado com a opção -p, como mostrado acima.
- Máquinas de cluster usando a opção --machine-file. Isso usa o login ssh sem uma senha para iniciar os fluxos de trabalho de Julia (no mesmo caminho que o host atual) nas máquinas especificadas.

As funções addprocs , rmprocs , worker e outras estão disponíveis como uma ferramenta de software para adicionar, remover e consultar processos em um cluster.
julia> using Distributed julia> addprocs(2) 2-element Array{Int64,1}: 2 3
O módulo Distributed deve ser explicitamente carregado no processo principal antes de chamar addprocs . Ele fica automaticamente disponível para fluxos de trabalho. Observe que os trabalhadores não executam o script de inicialização ~/.julia/config/startup.jl nem sincronizam seu estado global (como variáveis globais, definições de novos métodos e módulos carregados) com qualquer um dos outros processos em execução. Outros tipos de clusters podem ser suportados escrevendo seu próprio ClusterManager , conforme descrito abaixo na seção ClusterManager .
Ações de dados
O envio de mensagens e a movimentação de dados compõem a maior parte da sobrecarga em um programa distribuído. Reduzir o número de mensagens e a quantidade de dados enviados é fundamental para obter desempenho e escalabilidade. Para isso, é importante entender a movimentação de dados realizada pelas várias construções de programação distribuída de Julia.
fetch pode ser considerada uma operação explícita de movimentação de dados, pois solicita diretamente a movimentação de um objeto para a máquina local. @spawn (e várias construções relacionadas) também move os dados, mas isso não é tão óbvio, portanto pode ser chamado de operação implícita de movimentação de dados. Considere estas duas abordagens para construir e quadrar uma matriz aleatória:
Tempos da maneira:
julia> A = rand(1000,1000); julia> Bref = @spawn A^2; [...] julia> fetch(Bref);
método dois:
julia> Bref = @spawn rand(1000,1000)^2; [...] julia> fetch(Bref);
A diferença parece trivial, mas na verdade é bastante significativa devido ao comportamento do @spawn . No primeiro método, uma matriz aleatória é construída localmente e depois enviada para outro processo, onde é quadrada. No segundo método, uma matriz aleatória é construída e elevada ao quadrado em outro processo. Portanto, o segundo método envia muito menos dados que o primeiro. Neste exemplo de brinquedo, os dois métodos são fáceis de distinguir e escolher. No entanto, em um programa real, projetar a movimentação de dados pode ser muito caro e provavelmente uma medida.
Por exemplo, se o primeiro processo precisar da matriz A, o primeiro método poderá ser melhor. Ou, se a computação A for cara e usar apenas o processo atual, movê-lo para outro processo pode ser inevitável. Ou, se o processo atual tiver muito pouco em comum entre a spawn e a fetch(Bref) , talvez seja melhor eliminar completamente a simultaneidade. Ou imagine que o rand(1000, 1000) substituído por uma operação mais cara. Então pode fazer sentido adicionar outra declaração de spawn apenas para esta etapa.
Variáveis globais
Expressões executadas remotamente por spawn ou fechamentos especificados para execução remota usando remotecall , podem se referir a variáveis globais. As ligações globais no módulo Main são tratadas de maneira um pouco diferente das ligações globais em outros módulos. Considere o seguinte snippet de código:
A = rand(10,10) remotecall_fetch(()->sum(A), 2)
Neste caso, a sum DEVE ser definida no processo remoto. Observe que A é uma variável global definida no espaço de trabalho local. O trabalhador 2 não possui uma variável chamada A na seção Main . Enviar a função de fechamento () -> sum(A) para o trabalhador 2 faz com que Main.A seja definido em 2. Main.A continua existindo no trabalhador 2, mesmo após o remotecall_fetch chamada remotecall_fetch .

Chamadas remotas com referências globais incorporadas (apenas no módulo principal) gerenciam variáveis globais da seguinte maneira:
- Novas ligações globais serão criadas nas estações de trabalho de destino se forem referenciadas como parte de uma chamada remota.
- As constantes globais também são declaradas como constantes em nós remotos.
- Os Globals são reenviados ao funcionário de destino apenas no contexto de uma chamada remota e somente se seu valor foi alterado. Além disso, o cluster não sincroniza ligações globais entre nós. Por exemplo:
A = rand(10,10) remotecall_fetch(()->sum(A), 2)
A execução do fragmento acima leva ao fato de que Main.A no funcionário 2 tem um valor diferente de Main.A no funcionário 3, enquanto o valor de Main.A no nó 1 é zero.
Como você provavelmente entendeu, embora a memória associada às variáveis globais possa ser coletada quando elas são reatribuídas ao dispositivo mestre, essas ações não são executadas para os trabalhadores, pois as ligações continuam a funcionar. claro! pode ser usado para reatribuir manualmente determinadas variáveis globais para nothing se elas não forem mais necessárias. Isso liberará qualquer memória associada a eles como parte do ciclo normal de coleta de lixo. Portanto, os programas devem ter cuidado ao acessar variáveis globais em chamadas remotas. De fato, sempre que possível, é melhor evitá-los. Se você precisar fazer referência a variáveis globais, considere usar blocos let para localizar variáveis globais. Por exemplo:
julia> A = rand(10,10); julia> remotecall_fetch(()->A, 2); julia> B = rand(10,10); julia> let B = B remotecall_fetch(()->B, 2) end; julia> @fetchfrom 2 InteractiveUtils.varinfo() name size summary ––––––––– ––––––––– –––––––––––––––––––––– A 800 bytes 10×10 Array{Float64,2} Base Module Core Module Main Module
É fácil ver que a variável global A definida no trabalhador 2, mas B gravada como uma variável local e, portanto, a ligação para B não existe no trabalhador 2.
Loops paralelos

Felizmente, muitos cálculos úteis de simultaneidade não requerem movimentação de dados. Um exemplo típico é uma simulação de Monte Carlo, na qual vários processos podem processar simultaneamente testes de simulação independentes. Podemos usar o @spawn para lançar moedas em dois processos. Primeiro, escreva a seguinte função em count_heads.jl :
function count_heads(n) c::Int = 0 for i = 1:n c += rand(Bool) end c end
A função count_heads simplesmente adiciona n bits aleatórios. Veja como podemos fazer alguns testes em duas máquinas e adicionar os resultados:
julia> @everywhere include_string(Main, $(read("count_heads.jl", String)), "count_heads.jl") julia> a = @spawn count_heads(100000000) Future(2, 1, 6, nothing) julia> b = @spawn count_heads(100000000) Future(3, 1, 7, nothing) julia> fetch(a)+fetch(b) 100001564
Este exemplo demonstra um padrão de programação paralela poderoso e frequentemente usado. Muitas iterações são executadas independentemente em vários processos e, em seguida, seus resultados são combinados usando alguma função. O processo de união é chamado de redução, porque geralmente reduz a classificação do tensor: o vetor de números é reduzido para um número ou a matriz é reduzida para uma linha ou coluna, etc. No código, isso geralmente se parece com isso: padrão x = f(x, v [i]) , onde x é a bateria, f é a função de redução e v[i] são os elementos a serem reduzidos.
É desejável que f seja associativo para que não importe em que ordem as operações são executadas. Observe que o uso deste modelo com count_heads pode ser generalizado. Usamos duas declarações explícitas de spawn , o que limita a simultaneidade a dois processos. Para executar em qualquer número de processos, podemos usar um loop for paralelo operando na memória distribuída, que pode ser gravada em Julia usando o Distributed , por exemplo:
nheads = @distributed (+) for i = 1:200000000 Int(rand(Bool)) end
( (+) ). . .
, for , . , , , . , , . , :
a = zeros(100000) @distributed for i = 1:100000 a[i] = i end
, . , . , Shared Arrays , , :
using SharedArrays a = SharedArray{Float64}(10) @distributed for i = 1:10 a[i] = i end
«» , :
a = randn(1000) @distributed (+) for i = 1:100000 f(a[rand(1:end)]) end
f , . , , . , Future , . Future , fetch , , @sync , @sync distributed for .
, (, , ). , , Julia pmap . , :
julia> M = Matrix{Float64}[rand(1000,1000) for i = 1:10]; julia> pmap(svdvals, M);
pmap , . , distributed for , , , . pmap , distributed . distributed for .
(Shared Arrays)

Shared Arrays . DArray , SharedArray . DArray , ; , SharedArray .
SharedArray — , , . Shared Array SharedArrays , . SharedArray ( ) , , . SharedArray , . , Array , SharedArray , sdata . AbstractArray sdata , sdata Array . :
SharedArray{T,N}(dims::NTuple; init=false, pids=Int[])
N - T dims , pids . , , pids ( , ).
init initfn(S :: SharedArray) , . , init , .
:
julia> using Distributed julia> addprocs(3) 3-element Array{Int64,1}: 2 3 4 julia> @everywhere using SharedArrays julia> S = SharedArray{Int,2}((3,4), init = S -> S[localindices(S)] = myid()) 3×4 SharedArray{Int64,2}: 2 2 3 4 2 3 3 4 2 3 4 4 julia> S[3,2] = 7 7 julia> S 3×4 SharedArray{Int64,2}: 2 2 3 4 2 3 3 4 2 7 4 4
SharedArrays.localindices . , , :
julia> S = SharedArray{Int,2}((3,4), init = S -> S[indexpids(S):length(procs(S)):length(S)] = myid()) 3×4 SharedArray{Int64,2}: 2 2 2 2 3 3 3 3 4 4 4 4
, , . Por exemplo:
@sync begin for p in procs(S) @async begin remotecall_wait(fill!, p, S, p) end end end
. pid , , ( S ), pid .
«»:
q[i,j,t+1] = q[i,j,t] + u[i,j,t]
, , , , , : q [i,j,t] , q[i,j,t+1] , , , q[i,j,t] , q[i,j,t+1] . . . , (irange, jrange) , :
julia> @everywhere function myrange(q::SharedArray) idx = indexpids(q) if idx == 0
:
julia> @everywhere function advection_chunk!(q, u, irange, jrange, trange) @show (irange, jrange, trange)
SharedArray
julia> @everywhere advection_shared_chunk!(q, u) = advection_chunk!(q, u, myrange(q)..., 1:size(q,3)-1)
, :
julia> advection_serial!(q, u) = advection_chunk!(q, u, 1:size(q,1), 1:size(q,2), 1:size(q,3)-1);
@distributed :
julia> function advection_parallel!(q, u) for t = 1:size(q,3)-1 @sync @distributed for j = 1:size(q,2) for i = 1:size(q,1) q[i,j,t+1]= q[i,j,t] + u[i,j,t] end end end q end;
, :
julia> function advection_shared!(q, u) @sync begin for p in procs(q) @async remotecall_wait(advection_shared_chunk!, p, q, u) end end q end;
SharedArray , ( julia -p 4 ):
julia> q = SharedArray{Float64,3}((500,500,500)); julia> u = SharedArray{Float64,3}((500,500,500));
JIT- @time :
julia> @time advection_serial!(q, u); (irange,jrange,trange) = (1:500,1:500,1:499) 830.220 milliseconds (216 allocations: 13820 bytes) julia> @time advection_parallel!(q, u); 2.495 seconds (3999 k allocations: 289 MB, 2.09% gc time) julia> @time advection_shared!(q,u); From worker 2: (irange,jrange,trange) = (1:500,1:125,1:499) From worker 4: (irange,jrange,trange) = (1:500,251:375,1:499) From worker 3: (irange,jrange,trange) = (1:500,126:250,1:499) From worker 5: (irange,jrange,trange) = (1:500,376:500,1:499) 238.119 milliseconds (2264 allocations: 169 KB)
advection_shared! , , .
, . , , .
, , , .
- Julia
, , , .
, , -. , onde — . - , .. , .
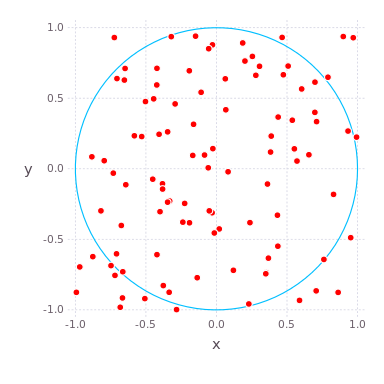
( , ) ( ) , , , . , , . compute_pi (N) , , .
function compute_pi(N::Int)
, , . : , , 25 .
Julia Pi.jl ( Sublime Text , ):
C:\Users\User\AppData\Local\Julia-1.1.0\bin\julia -p 4 julia> include("C:/Users/User/Desktop/Pi.jl")
using Distributed addprocs(4)
Jupyter
Pi.jl @everywhere function compute_pi(N::Int) n_landed_in_circle = 0
, :
julia> @time parallel_pi_computation(1000000000, ncores = 1) 6.818123 seconds (1.96 M allocations: 99.838 MiB, 0.42% gc time) 3.141562892 julia> @time parallel_pi_computation(1000000000, ncores = 1) 5.081638 seconds (1.12 k allocations: 62.953 KiB) 3.141657252 julia> @time parallel_pi_computation(1000000000, ncores = 2) 3.504871 seconds (1.84 k allocations: 109.382 KiB) 3.1415942599999997 julia> @time parallel_pi_computation(1000000000, ncores = 4) 3.093918 seconds (1.12 k allocations: 71.938 KiB) 3.1416889400000003 julia> pi ? = 3.1415926535897...
JIT - — . , Julia . , ( Multi-Threading, Atomic Operations, Channels Coroutines).
, , . MPI.jl MPI ,
DistributedArrays.jl .
GPU, :
- ( C) OpenCL.jl CUDAdrv.jl OpenCL CUDA.
- ( Julia) CUDAnative.jl CUDA .
- , , CuArrays.jl CLArrays.jl
- , ArrayFire.jl GPUArrays.jl
- -
- Kynseed
, , . !