Conecte os autômatos celulares ao algoritmo genético e veja o que acontece.
O artigo contém Gif (tráfego!) E imagens contrastantes. Epilépticos podem ter uma convulsão epiléptica.Regras para autômatos celulares
O autômato celular mais simples é um autômato celular unidimensional (também existem autômatos de dimensão zero - falaremos sobre eles abaixo). Em um autômato celular unidimensional, temos uma matriz unidimensional, cujas células (células) podem assumir um dos dois estados (1/0, verdadeiro / falso, branco / preto, vivo / morto). O próximo estado da célula na matriz é determinado pelo estado atual da célula e pelo estado de duas células vizinhas, de acordo com alguma regra.
Total existe
23=8 combinações de estados celulares e duas células vizinhas:

Em seguida, para cada uma das combinações, anotamos o estado da célula para a próxima iteração (para o próximo estado do autômato):
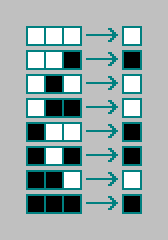
Tem uma regra para um autômato celular. As regras para autômatos celulares unidimensionais são codificadas com 8 bits ("código de tungstênio"). Total existe
28=256 autômatos celulares elementares:
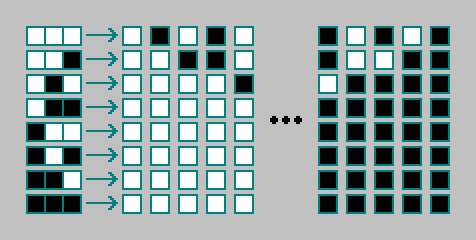
256 máquinas podem ser classificadas manualmente. Nós não vamos insistir neles. Calculamos o número de regras existentes para autômatos celulares bidimensionais.
Um autômato celular bidimensional usa uma matriz bidimensional. Cada célula possui 8 vizinhos nas proximidades de Moore (há também uma vizinhança de von Neumann na qual as células diagonais não são levadas em consideração. Não consideraremos isso no artigo):

Por conveniência, escrevemos as células em uma linha (usaremos a ordem selecionada posteriormente neste artigo):
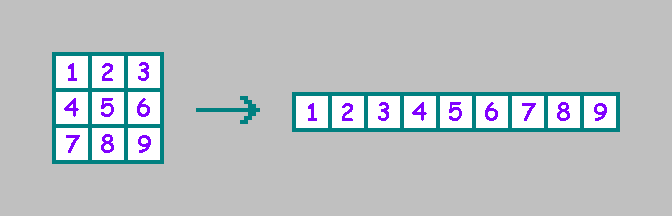
Para um autômato celular bidimensional, existe
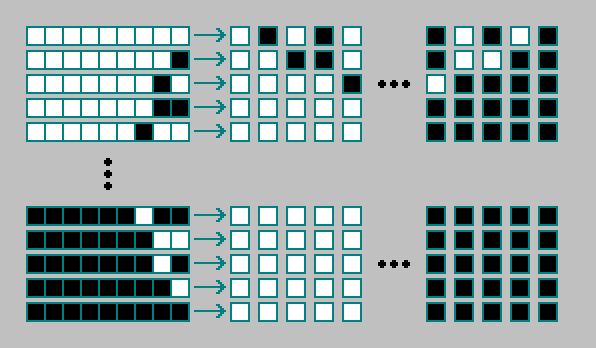
29=512 combinações de estados celulares e 8 células vizinhas:

A regra para um autômato celular bidimensional é codificada com 512 bits. Total existe
2512 autômatos celulares bidimensionais:
Número:
2512 approx1.340781 times10154
mais
átomos no universo observável (
1080 )
Manualmente, esse número de máquinas não pode ser resolvido. Se olharmos para um autômato a cada segundo - durante a existência do Universo, teríamos conseguido olhar para tudo
approx4.35 times1017 máquinas automáticas.
A enumeração simples não funciona, mas com a ajuda de um algoritmo genético, podemos encontrar autômatos que melhor se encaixam em certos critérios predefinidos.
Vamos programar em JavaScript. Todos os fragmentos de código estão ocultos em spoilers para não confundir os leitores que não estão familiarizados com as linguagens de programação.
Autômato celular bidimensional
Escrevemos um autômato celular bidimensional com uma regra aleatória. Armazenaremos a regra na matriz de regras, cujo tamanho rulesize = 512:
Preencha a matriz de regrasvar rulesize=512; var rule=[]; for(var i=0;i<rulesize;i++) rule[i]=Math.round(Math.random());
Em seguida, preencha o estado inicial da máquina com uma casa aleatória:
Nós preenchemos o estado inicial da máquina var sizex=89; var sizey=89; var size=2; var a=[]; for(var x=0;x<sizex;x++){ a[x]=[] for(var y=0;y<sizey;y++){ a[x][y]=Math.round(Math.random()); if(a[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } }
(aqui e mais adiante no artigo, conforme a largura e a altura da máquina, um número aleatório é obtido - não é muito grande nem muito pequeno número ímpar 89)A função que calcula o seguinte estado do autômato tem a seguinte aparência (para não desarrumar, removeu a inicialização da tela):
Consideramos o seguinte estado do autômato function countpoints(){ var temp=[]; var xm, xp, ym, yp, q; for(var x=0;x<sizex;x++){ xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0; temp[x]=[]; for(var y=0;y<sizey;y++){ ym=y-1; if(ym==-1) ym=sizey-1; yp=y+1; if(yp==sizey) yp=0; q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q]; if(temp[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } } a=temp; }
As variáveis xm e xp armazenam as coordenadas X do vizinho à esquerda e o vizinho à direita (x menos ex mais). As variáveis ym e yp armazenam as coordenadas Y correspondentes.
Aqui:
O campo da máquina é enrolado em um bagel xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0;
definimos condições de contorno periódicas (o campo do autômato é a superfície do toro).
Seguinte:
... mais q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q];
na ordem acima, escreva o conteúdo das células em uma string. Traduzimos a string em um número decimal. Para essa combinação, encontramos na matriz de regras o estado que a célula com as coordenadas x e y deve assumir.
Opção otimizada q=a[xm][ym]; q=(q<<1)+a[x][ym]; q=(q<<1)+a[xp][ym]; q=(q<<1)+a[xm][y]; q=(q<<1)+a[x][y]; q=(q<<1)+a[xp][y]; q=(q<<1)+a[xm][yp]; q=(q<<1)+a[x][yp]; q=(q<<1)+a[xp][yp]; temp[x][y]=rule[q];
Após todas as iterações, substitua o estado anterior do autômato por um novo:
substitua o estado anterior por um novo Desenhamos um autômato usando a função setInterval:
setInterval timerId = setInterval(function() { countpoints(); }, 1);
Executar no navegadorEu recomendo iniciar a máquina com regras aleatórias 10 a 20 vezes antes de continuar lendo o artigo.
Podemos operar a máquina por muito tempo com diferentes regras aleatórias. A imagem que obtemos não difere da imagem na tela da TV na ausência de um sinal:

Em seguida, vamos prosseguir com a configuração de nossa “TV” usando o algoritmo genético.
Algoritmo genético
O tamanho da população inicial é de 200 máquinas (indivíduos). Para regras, em vez de uma matriz unidimensional de regra, usaremos uma matriz bidimensional de população. O primeiro índice (n) é o número do indivíduo na população.
Crie uma população var PopulationSize=200; var rulesize=512; var population=[]; var fitness=[]; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }
A matriz de fitness contém os coeficientes de fitness de cada indivíduo. Essa matriz é preenchida no processo de seleção. Após a seleção, iniciamos o processo evolutivo.
Processo evolutivo
Da nossa população, tomamos metade dos indivíduos mais adaptados (de acordo com o coeficiente de condicionamento físico). A metade restante é destruída. Em seguida, pegamos dois indivíduos sobreviventes e os cruzamos.

Para cruzar, selecione uma posição aleatória nos genótipos de dois ancestrais. Antes dessa posição, pegamos genes de um ancestral, depois dessa posição - de outro. Colocamos os genes selecionados no genótipo em um descendente. Os genes restantes são para outro. Colocamos dois ancestrais e dois descendentes em uma nova população. Ao mesmo tempo, cada indivíduo participa da travessia uma vez.
Mutações. Com uma probabilidade de 5%, um gene selecionado aleatoriamente sofre mutação (inversa) em cada indivíduo. Se você aumentar a probabilidade de mutações, haverá mais mutantes bem-sucedidos, mas, ao mesmo tempo, um mutante bem-sucedido pode não ter tempo para deixar a prole bem-sucedida antes que ela mude novamente sem êxito. Voltaremos a esse problema mais tarde.
Função evoluir (); function evolute(){ var sizehalf=PopulationSize/2; var sizequarter=sizehalf/2; var arrayt=[]; for(var n=0; n<PopulationSize; n++) arrayt[n]=[population[n], fitness[n]]; arrayt.sort(sortf); arrayt.length=sizehalf; population=[]; fitness=[]; for(var i=0; i<sizequarter; i++){ var i0=i*4; var i1=i*4+1; var i2=i*4+2; var i3=i*4+3; var removed1=Math.floor(Math.random()*(arrayt.length)); var parent1f = arrayt.splice(removed1,1); var parent1=parent1f[0][0]; var removed2=Math.floor(Math.random()*(arrayt.length)); var parent2f = arrayt.splice(removed2,1); var parent2=parent2f[0][0]; var child1=[]; var child2=[]; var qen=Math.floor(Math.random()*rulesize); var temp0=parent1; var temp1=parent2; var temp2=temp0.splice(qen,rulesize); var temp3=temp1.splice(qen,rulesize); var parent1=temp0.concat(temp2); var parent2=temp1.concat(temp3); var child1=temp1.concat(temp2); var child2=temp0.concat(temp3); population[i0]=parent1; population[i1]=parent2; population[i2]=child1; population[i3]=child2; fitness[i0]=0; fitness[i1]=0; fitness[i2]=0; fitness[i3]=0; } var mutation=document.getElementById("mutatepercent").value*1; var m=100/mutation; var m2=0;
Seleção natural
Antes de iniciar o processo evolutivo, a seleção deve ser feita. A seleção pode ser natural e artificial. A seleção artificial é feita manualmente - um pouco mais tarde. Para a seleção natural, definiremos alguns critérios e selecionaremos as máquinas que melhor atendem aos critérios fornecidos.
Quais critérios podem ser determinados com antecedência? Pegue o mais fácil. Nossa "TV" está piscando demais. Salvamos dois estados do autômato celular - em 99 e em 100 iterações. Conte o número de células que não foram alteradas. O número resultante será usado como um coeficiente de condicionamento físico. Obviamente, um critério não é suficiente para nós. É fácil selecionar manualmente o autômato que melhor atenda ao critério especificado: o autômato [0,0,0, ..., 0] e o autômato [1,1,1, ..., 1]. Na primeira iteração, esses dois autômatos são preenchidos com zeros ou uns e param de mudar de estado. Definimos o segundo critério: a diferença entre o número de 0 e 1 (células) na máquina não excede 100 (o número é obtido "do bulldozer").
array1 - estado do autômato na 99ª iteração. array2 - na 100ª iteração:
Consideramos function countfitness(array1, array2){ var sum=0; var a0=0; var a1=0; for(var x=0;x<sizex;x++){ for(var y=0;y<sizey;y++){ if(array1[x][y]==array2[x][y]) sum++; if(array1[x][y]==0){ a0++; }else{ a1++; } } } if(Math.abs(a0-a1)<100) return sum; return 0; }
Começamos. A solução ideal foi encontrada no 421º ciclo de evolução. No gráfico você pode ver o progresso:
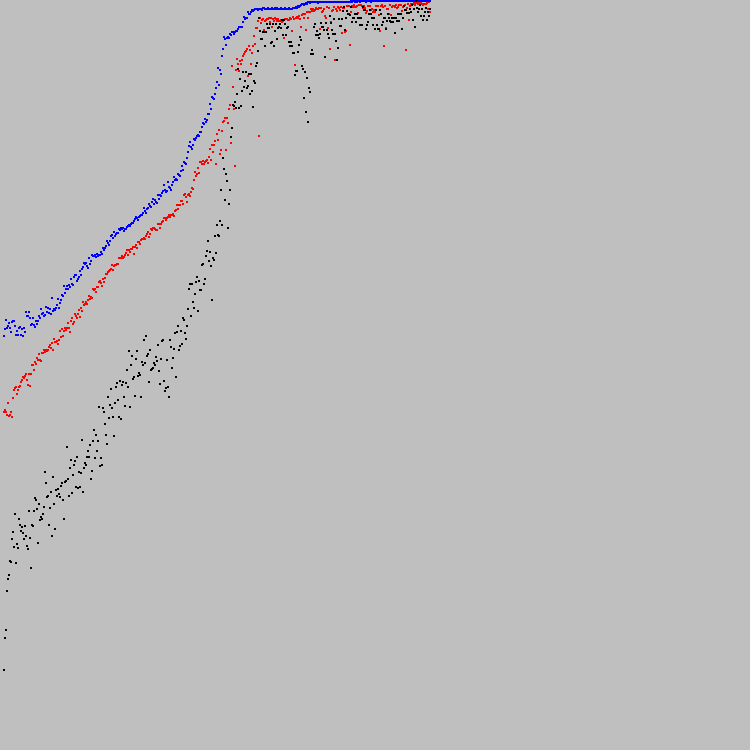
O gráfico é dimensionado ao longo do eixo Y. O ponto inferior é 0, o ponto mais alto é 7921. Obviamente, 7921 é a solução ideal (todas as células na máquina 89x89 atendem ao critério especificado). Após 100 iterações, nenhuma célula altera seu estado.
Os pontos azuis no gráfico são os melhores indivíduos da população. Os vermelhos são os piores (apenas os indivíduos que atendem ao segundo critério são levados em consideração). Pontos pretos - o coeficiente médio de aptidão para toda a população (levando em consideração indivíduos que não atendem ao segundo critério). O segundo critério (o equilíbrio entre branco e preto) é muito difícil. Alguns autômatos não atendem ao segundo critério, mesmo após 421 ciclos de evolução. Portanto, os pontos pretos estão abaixo do vermelho.
O pool genético da população (indivíduos ao longo do eixo Y, genes ao longo do eixo X):

Vamos ver qual canal nossa "TV" capturou:

A solução encontrada não é a única ótima. Se repetirmos a evolução (com genótipos iniciais aleatórios), encontraremos outras soluções ótimas. Um deles:

Alterar os critérios de seleção.
Consideraremos o número de células para as quais um padrão aparece nas proximidades de Moore da ordem 2. Vamos pegar o padrão mais simples:
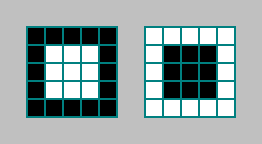
Esse critério é interessante, pois verificamos 25 células, enquanto o autômato calcula o estado da célula com base nos estados de 9 células.
O critério é muito rigoroso. Se pegarmos um autômato aleatório, depois de 100 iterações, fica assim:

Nenhuma célula desse autômato atende ao critério especificado. Portanto, suavizamos um pouco o critério:
- Vamos cometer um erro no padrão.
- Não procuraremos o padrão na última iteração, mas nas últimas 50 iterações.
O segundo critério (o equilíbrio entre branco e preto) é removido.
Começamos. Gráfico:
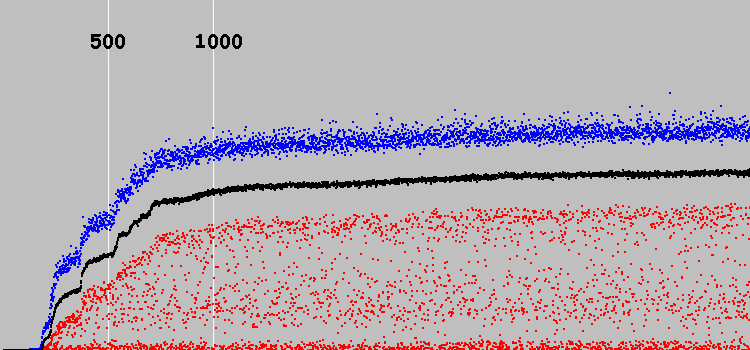
O eixo y é arbitrário. (Na máquina anterior, a solução ideal é 7921. Nesta máquina, cerca de 30.)
Eixo X - 3569 ciclos de evolução. Duas linhas verticais brancas marcam 500 e 1000 ciclos de evolução.
Pontos azuis - o melhor indivíduo da população, vermelho - o pior, preto - a proporção média para toda a população.
A solução foi encontrada nos primeiros 500 ciclos de evolução. Nos próximos 500 ciclos, a solução melhora. E então o sistema praticamente deixa de evoluir.
Nas três figuras abaixo: 500 ciclos, 1000 ciclos e 3569 ciclos de evolução:



Pool de genes (3569):

Em dinâmica:

Na imagem abaixo, você pode ver como o oscilador (planador) é formado nesta máquina:

Podemos iniciar a máquina com o estado inicial em que uma célula está preenchida. Em seguida, corrija todas as combinações de células encontradas nas iterações a seguir do autômato. Uma matriz de genes (genótipo de um autômato) é uma matriz de todas as combinações possíveis. Tendo isolado apenas as combinações que ocorrem, podemos observar facilmente todos os genes envolvidos na formação do oscilador. Barras cinzas são genes que não participam da formação do oscilador:

Mutações nesses genes não se enraízam devido ao fato de perturbarem a formação de padrões.
Em nossa máquina, um padrão (quadrado) é formado apenas em torno de uma célula preta. Vamos tentar iniciar o processo evolutivo junto com o segundo critério: a diferença entre o número de células brancas e pretas não excede 400.
Iniciamos 3569 ciclos de evolução. Gráfico:
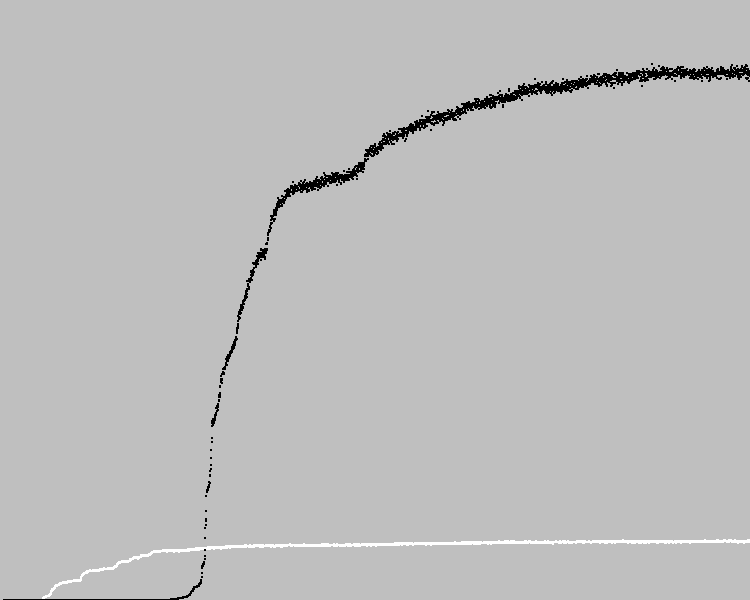
Pontos pretos no gráfico são o coeficiente médio de condicionamento físico em uma população. Pontos brancos - o coeficiente médio de adequação da máquina anterior. Encontrei uma solução com um erro no padrão.
Pool de genes:

100 primeiras iterações:

Última (100) iteração:

Um pouco não é o resultado que esperávamos. Há quadrados pretos, brancos - não. Aperte o segundo critério: a diferença entre o número de células brancas e pretas não excede 100.
Iniciamos 14865 ciclos de evolução.
O gráfico compara os coeficientes médios de condicionamento das populações. Pontos azuis são a nossa metralhadora. Branco e preto são máquinas anteriores.

Um autômato evolui tão vigorosamente que pode parecer que não evolui. O segundo gráfico é escalado ao longo do eixo Y. Duas linhas brancas - 500 e 1000 ciclos.
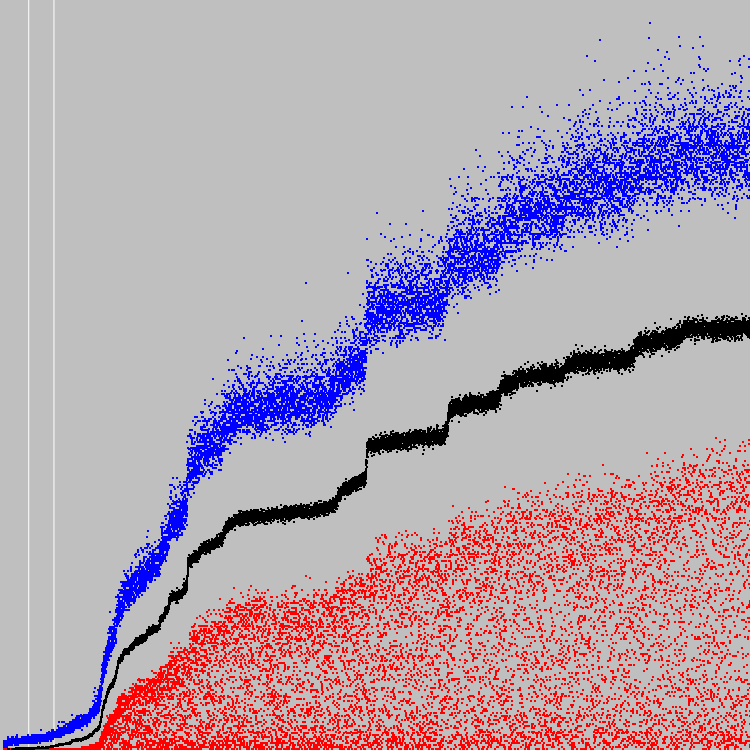
No melhor indivíduo, em média, 6 células correspondem a um determinado critério.
Vejamos uma máquina aleatória de uma população.
50 iterações:

Última (50) iteração:

Nenhum resultado aceitável encontrado. O segundo critério complica a pesquisa, portanto a recusaremos (não a usaremos mais adiante neste artigo). Vamos deixar esse padrão e procurar alguns outros padrões.
Padrão:

Começamos. 3000 ciclos de evolução. Gráfico:
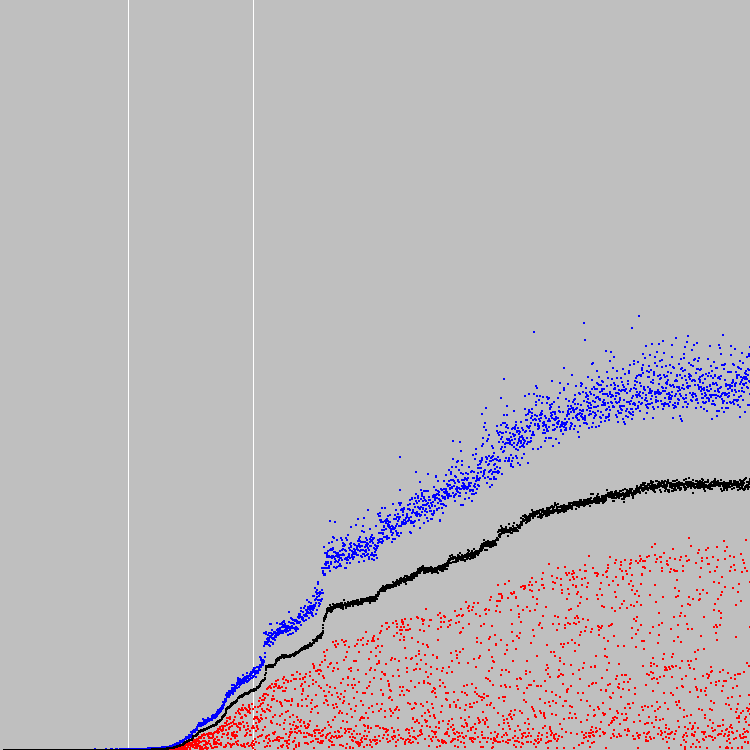
Pool de genes:

Em dinâmica (100 iterações):

Última (100) iteração:

Padrão:

Em máquinas anteriores, permitimos cometer um erro no padrão. Desta vez, vamos procurar o padrão exato.
Iniciamos 4549 ciclos de evolução. Gráfico:
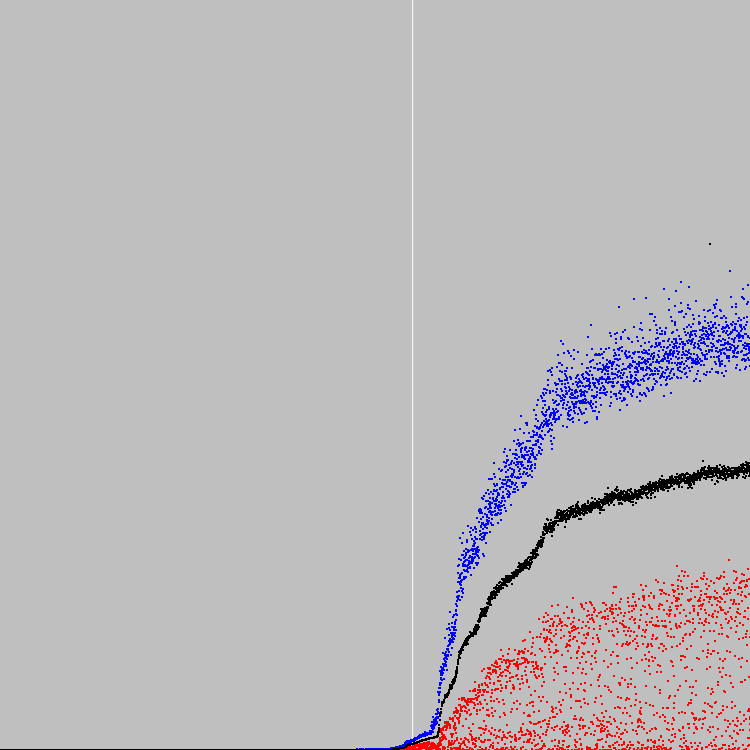
Linha vertical branca - 2500 ciclos de evolução. Nesse ponto (um pouco antes), a aptidão da população começou a crescer rapidamente. Salvou a população para procurar uma solução provisória. A solução intermediária acabou sendo muito mais interessante que a solução no 4549º ciclo de evolução.
Solução encontrada no 4549º ciclo de evolução:

Existem 100 iterações no GIF. Após um certo número de iterações (cerca de 500-2000), o estado do autômato é quase completamente ordenado (a altura e a largura do autômato são escolhidas especialmente por números ímpares, para que o autômato não possa ser completamente ordenado):

Um autômato com tamanhos pares de lados, após um certo número de iterações, assume um estado totalmente ordenado. 90x90 automático, aproximadamente 1200 iterações:

Solução intermediária (encontrada no 2500º ciclo de evolução):

Esse autômato também é capaz de processar um certo estado caótico inicial em um determinado estado finito ordenado (o estado final ordenado é a mudança do padrão ao longo do eixo X para a esquerda + várias células do oscilador).
A máquina 16x16 classificou em cerca de 100 iterações:

32x32 - cerca de 1000 iterações:

64x64 - cerca de 6000 iterações:

90x90 - cerca de 370000 iterações:

11x11 (dimensões ímpares do campo de autômato) - cerca de 178700 iterações:

O fuzil de assalto 13x13 não foi encomendado em um período de tempo aceitável.
Na figura abaixo, a máquina no campo 256x256 na 100.000ª iteração:

Eu recomendo olhar para esse autômato em dinâmica em um campo grande - é muito interessante observar o processo de auto-organização do caos nesse autômato:
executar em um navegadorConjunto genético da população intermediária:

Reiniciar o processo evolutivo permite encontrar outras soluções. Um deles:


Outro padrão:
Ao procurar um padrão, vamos novamente cometer um erro (sem erros, o sistema com o padrão selecionado não evolui).
Começamos. 5788 ciclos de evolução. Gráfico:
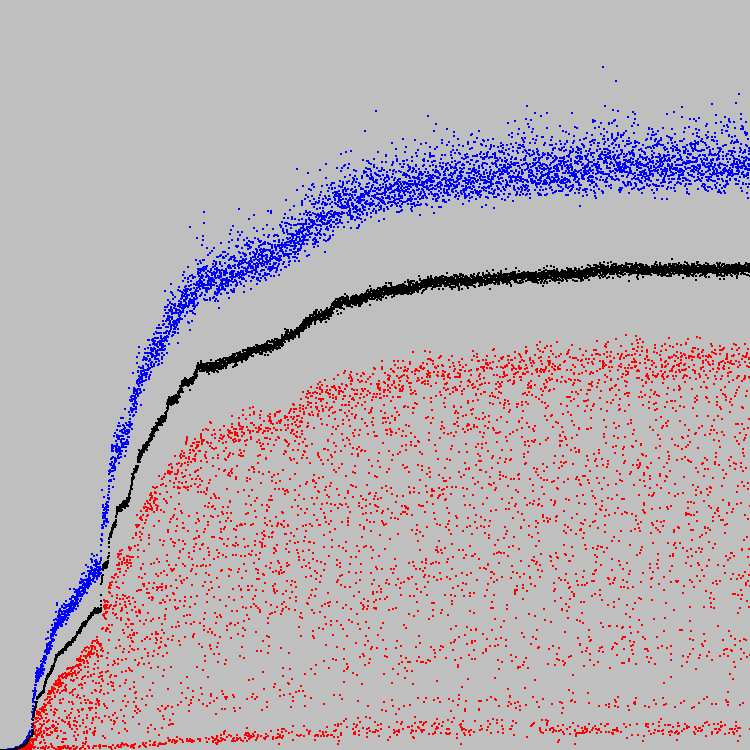
A escala é arbitrária.
Pool de genes:

Em dinâmica:

O estado ordenado do autômato (deslocamento do padrão para cima ao longo do eixo Y + várias células do oscilador):

É muito mais interessante observar não a própria máquina, mas os mutantes que aparecem nessa população:
No GIF, a máquina tem 256x256. 200 iterações. As iterações restantes podem ser
visualizadas no navegador .
Pode-se terminar com a seleção natural e passar para artificial, mas quero mostrar quanto
2512 um número enorme. Entre esse número de autômatos, podemos encontrar um autômato que desenha qualquer padrão dado (com alguma precisão para padrões mais complexos).
O seguinte padrão:

Em experimentos anteriores, contamos a soma de células em torno das quais um padrão é formado (se com um erro, adicione 1 à soma, se sem erros, adicione 2). A quantidade resultante foi usada como um fator de aptidão para o algoritmo genético.
Para um padrão mais complexo, esse método não funciona. Um autômato no qual um número menor de células corresponde mais a um determinado critério (o número de células que correspondem a um padrão na vizinhança de uma célula) sempre perde para um autômato no qual um número maior de células corresponde com menos precisão a um determinado critério. Como no exemplo com os quadrados acima:

Para o padrão desejado, na 100ª iteração de cada autômato na população, cercado por cada célula, consideraremos o número de células que correspondem ao padrão. Tomaremos apenas o melhor resultado para cada máquina. O número de células correspondentes ao padrão será usado como um fator de condicionamento físico. O padrão consiste em 7x17 = 119 células. Esse número será considerado a solução ideal. 6000 ciclos de evolução nos permitiram encontrar um autômato que desenha um padrão com 5 erros (114 células coincidem com o padrão).
Gráfico em escala arbitrária:
Um aumento na porcentagem de mutações não afetou a aptidão da população.
Existem muitos mutantes no pool genético da população:

Um autômato aleatório de uma população em dinâmica:

A melhor máquina na 100ª iteração:

Padrões pesquisados e encontrados:

Tendo brincado com os critérios de seleção, o tamanho do campo de autômatos e a porcentagem de mutações, acabou por melhorar a população e encontrar um autômato que comete apenas 3 erros no padrão.
Pool de genes:

Máquina na 100ª iteração:

Padrões pesquisados e encontrados:

2 errosNo processo de redação do artigo, o sistema continuou a evoluir. Para uma pesquisa mais precisa, o tamanho do campo da máquina foi aumentado para 513x513. Foi encontrado um autômato que comete apenas dois erros no padrão:

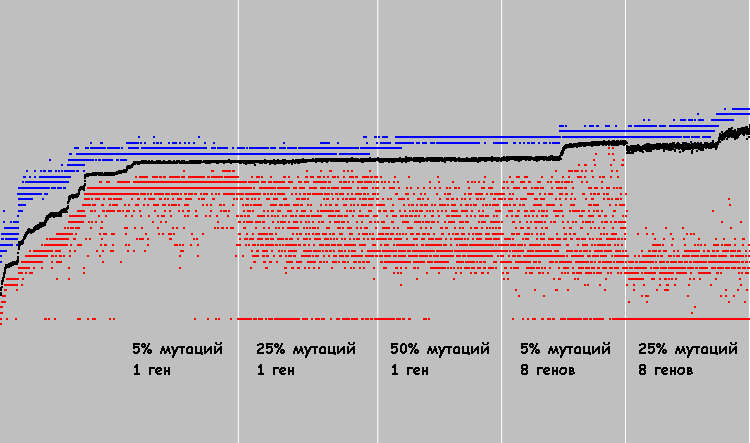
Em quatro gráficos, você pode ver como o sistema evolui com diferentes probabilidades de mutação (1 gene sofre mutação):
Pontos vermelhos são o coeficiente médio de condicionamento físico em uma população. Pontos pretos são o coeficiente de condicionamento físico de cada indivíduo. 3000 ciclos de evolução para cada sistema.
Grupos genéticos de populações (na mesma ordem):




Autômatos na 100ª iteração:




Vamos fazer outro experimento. O padrão é o mesmo. Os genótipos iniciais são preenchidos com genes aleatórios. A probabilidade de mutações é de 5%. De 1 a 8 genes mudam (um número aleatório de genes mutantes é obtido para cada indivíduo). 100 ciclos de evolução.

O gráfico é um mapa de calor. O tamanho do ponto no gráfico é de 5 pixels. A origem é o canto superior esquerdo.
No eixo Y (de 0 a 100) - ciclos de evolução. No eixo X (de 0 a 119) - o número de células coincidentes com o padrão (para cada indivíduo da população, obtemos o melhor resultado). O brilho do ponto é o número de indivíduos com o resultado especificado (coordenada X).
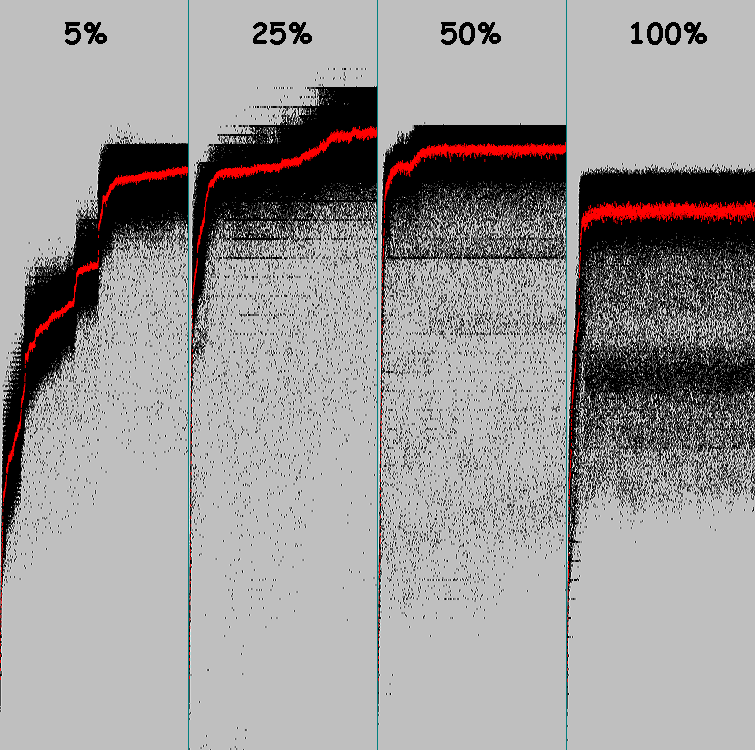
Execute o algoritmo genético 4 vezes com os mesmos parâmetros (100 ciclos, 5% de mutações, até 8 genes mutados). No gráfico, todas as 5 são iniciadas:

Os 5 seguintes iniciadores: 25% de mutações, até 8 genes são mutantes:

A amostra é pequena, mas podemos tirar conclusões sobre a eficácia do aumento da porcentagem de mutações.
A seguir, mostrarei a ineficiência do método de cruzamento usado no artigo.
Método usado anteriormente:

Em vez de dividir o genótipo em duas partes, os descendentes herdarão genes ancestrais aleatórios:
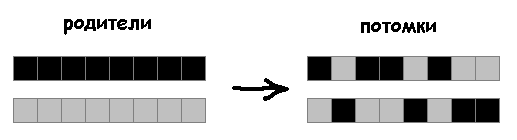
Mutações de 5%:

25%:

Em seguida, usaremos esse método de cruzamentos.
Sobre isso com acabamento de seleção natural. Se alguém tiver idéias interessantes sobre os critérios para a seleção natural - exprima-os nos comentários.
Para seleção artificial, usaremos
autômatos celulares de segunda ordem .
Autômato celular de segunda ordem
Considere um autômato celular de dimensão zero de primeira ordem (todos os autômatos celulares que consideramos acima são de primeira ordem). Um autômato celular de dimensão zero consiste em uma célula. Uma célula pode estar em um dos dois estados. O próximo estado da célula (t) é determinado pelo estado atual da célula (t-1). No total, existem 4 autômatos celulares de dimensão zero (entre eles um oscilador):
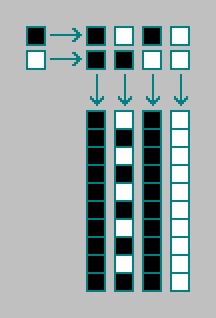
Em um autômato celular de segunda ordem, o próximo estado da célula (t) é determinado pelo estado atual (t-1) e pelo estado anterior da célula (t-2). No total, existem 4 combinações de dois estados celulares.
24=$1 - o número de autômatos celulares de dimensão zero de segunda ordem:

Esses autômatos celulares exibem osciladores mais complexos.
28=256 autômatos celulares de terceira ordem:
 216=65536
216=65536 autômatos celulares de quarta ordem não podem ser mostrados em uma imagem.
Pesquisa de autômatos celulares n ª ordem com um período de oscilação igual a n - A tarefa não é trivial e extremamente interessante. Este tópico merece um artigo separado.Nos autômatos celulares unidimensionais bidimensionais, o seguinte estado de uma célula é determinado pelo estado atual de três células e pelo estado anterior de uma célula:
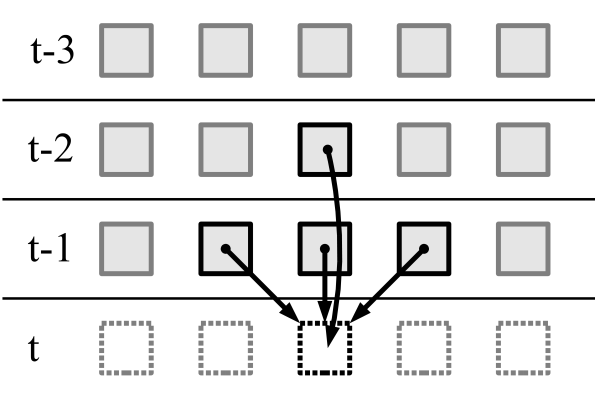
Existe
216=65536 autômatos celulares unidimensionais de segunda ordem.
Código:
var rule=[]; for(var i=0;i<16;i++) rule[i]=Math.round(Math.random()); var a=[]; var b=[]; var temp; for(var x=0;x<sizex;x++){ a[x]=0; b[x]=0; } b[63]=1; var xm, xp, q; for(var y=2;y<sizey;y++){ temp=[]; for(var x=0;x<sizex;x++){ xm=x-1; if(xm<0) xm=sizex+xm; xp=x+1; if(xp>=sizex) xp=xp-sizex; q=b[xm]; q=(q<<1)+b[x]; q=(q<<1)+b[xp]; q=(q<<1)+a[x]; temp[x]=rule[q]; if(temp[x]) context.fillRect(x*size, y*size, size, size); } a=b; b=temp; }
 0101101110011110:
0101101110011110: 0110000110010010:
0110000110010010: 0110011010010110:
0110011010010110: 1110011010010110:
1110011010010110: 0110111010000101:
0110111010000101: 1111101001110110:
1111101001110110: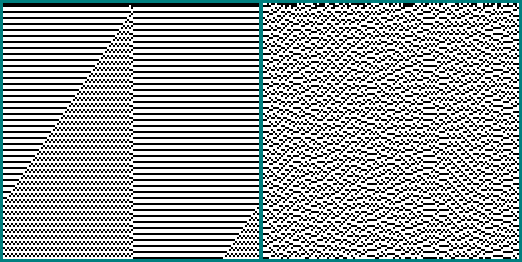 1001010001100000:
1001010001100000: A mesma máquina 256x256:
A mesma máquina 256x256: 512x512
512x512 Outras máquinas podem ser vistas aqui:máquina celular unidimensional de segunda ordem.Autômato celular unidimensional de terceira ordem.Autômatos celulares unidimensionais de segunda ordem podem ser encontrados no livro de Wolfram, A New Kind of Science.
Outras máquinas podem ser vistas aqui:máquina celular unidimensional de segunda ordem.Autômato celular unidimensional de terceira ordem.Autômatos celulares unidimensionais de segunda ordem podem ser encontrados no livro de Wolfram, A New Kind of Science.Seleção artificial
Como um autômato celular unidimensional de segunda ordem, em um autômato celular bidimensional de segunda ordem, usaremos uma célula adicional do estado anterior (t-2) do autômato.Por conveniência, colocamos esta célula no início da linha binária: a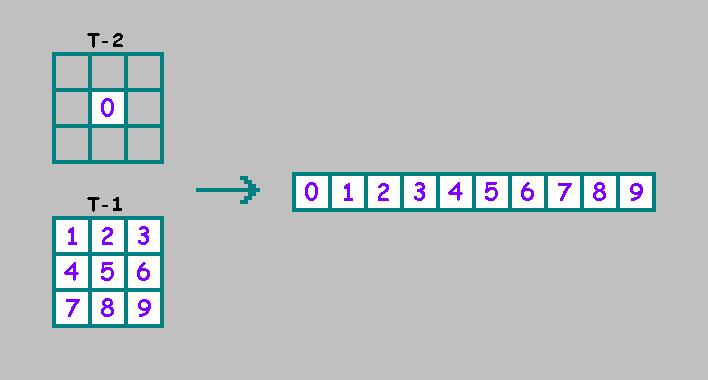 conveniência reside no fato de que, quando a primeira e a segunda metade do genótipo coincidem, o autômato pode ser considerado como um autômato de primeira ordem:
conveniência reside no fato de que, quando a primeira e a segunda metade do genótipo coincidem, o autômato pode ser considerado como um autômato de primeira ordem: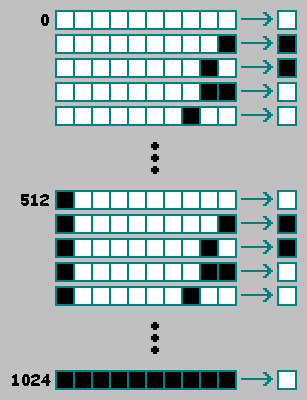 ao adicionar uma célula, aumentamos o número de autômatos existentes em2 512 vezes.2 512 × 2 512 = 2 1024 - o número de autômatos bidimensionais existentes de segunda ordem. Para seleção natural, determinamos algum critério e comparamos autômatos por esse critério. No processo de seleção artificial, selecionamos as máquinas manualmente, usando algum princípio indistinto: "essa máquina é interessante, mas isso não é muito". Esse princípio não permite escolher a melhor máquina entre máquinas aleatórias:Existem várias maneiras de resolver esse problema. Proponho considerar quatro maneiras.
ao adicionar uma célula, aumentamos o número de autômatos existentes em2 512 vezes.2 512 × 2 512 = 2 1024 - o número de autômatos bidimensionais existentes de segunda ordem. Para seleção natural, determinamos algum critério e comparamos autômatos por esse critério. No processo de seleção artificial, selecionamos as máquinas manualmente, usando algum princípio indistinto: "essa máquina é interessante, mas isso não é muito". Esse princípio não permite escolher a melhor máquina entre máquinas aleatórias:Existem várias maneiras de resolver esse problema. Proponho considerar quatro maneiras.





1. No estado inicial da máquina, uma célula é preenchida
Uma maneira é observar o desenvolvimento de um autômato celular, no estado inicial do qual uma célula é preenchida.Enchemos a população inicial com máquinas aleatórias. Várias máquinas da população inicial (30 iterações para cada):


Esses dois estão piscando Um pequeno número de autômatos com comportamento menos caótico está presente na população. Vamos selecioná-los para cruzamento:




 20 máquinas aleatórias da população inicial (estado das máquinas na 30ª iteração):
20 máquinas aleatórias da população inicial (estado das máquinas na 30ª iteração): Após três ciclos de evolução:
Após três ciclos de evolução: Após oito ciclos de evolução:
Após oito ciclos de evolução: Oito ciclos de evolução foram suficientes para encher toda a população com uma máquina com uma certa característica (uma máquina que desenha triângulos) .
Oito ciclos de evolução foram suficientes para encher toda a população com uma máquina com uma certa característica (uma máquina que desenha triângulos) .2. O genótipo é parcialmente preenchido
Se a proporção de unidades e zeros no genótipo for violada, a proporção de unidades e zeros no fenótipo será violada.No genótipo (regra) do autômato, as seguintes condições celulares são registradas para todas as combinações possíveis da célula e das células vizinhas. Se houver mais zeros (ou uns) no genótipo, então zeros (ou uns) se acumulam nos seguintes estados do autômato. É interessante observar a correlação entre a razão de uns e zeros no genótipo e a razão de uns e zeros no fenótipo.Crie um gráfico.Crie uma população de 200 máquinas. Enchemos os genótipos com zeros (1024 genes no genótipo de um autômato bidimensional de segunda ordem). Seguinten genes são preenchidos com unidades. Para a primeira populaçãon = 0 , para a 513ª populaçãon = 512 .
Ao longo do eixo x é o número da população. Ao longo do eixomarca y (com pontos brancos) a razão de uns e zeros no pool genético da população. Temos uma hipérbole:para cada autômato (com um tamanho de campo de 89x89), consideramos 100 iterações. Na 100ª iteração, contamos o número de um e zeros no estado (fenótipo) de cada autômato. Marcamos no gráfico a razão de unidades e zeros (o número total de todas as unidades é dividido pelo número total de todos os zeros). Temos uma curva: emvez da razão total de uns e zeros em todos os fenótipos, é possível observar a razão de uns e zeros em cada fenótipo:no lado esquerdo do gráfico, existem pontos com o maior desvio do valor médio. Pode-se supor que esses são autômatos nos genótipos em que o gene zero é igual à unidade. Suposto - verificado. Definimos o gene zero sempre igual a zero. Desenhamos um novo gráfico: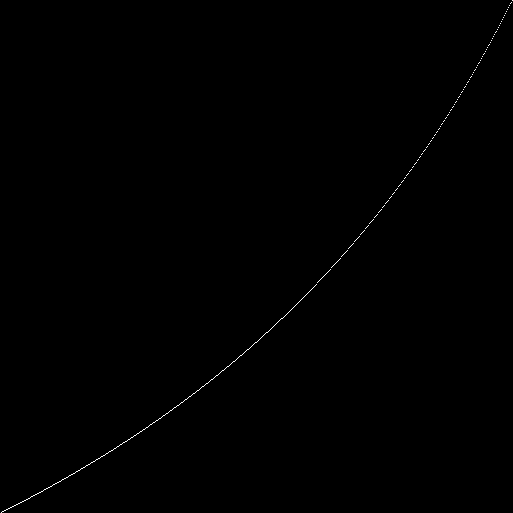
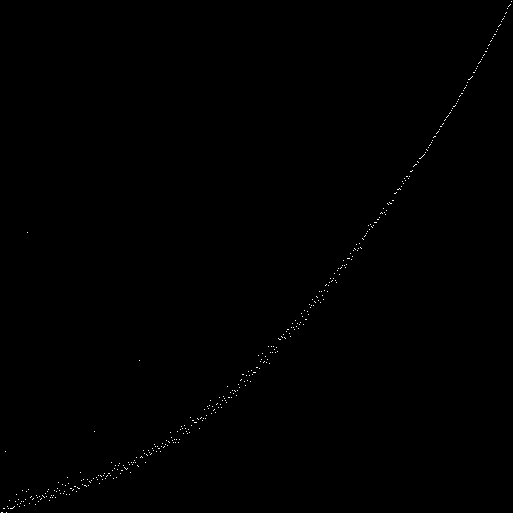

 Compare com máquinas nas quais o gene zero é sempre igual a um:
Compare com máquinas nas quais o gene zero é sempre igual a um: nas máquinas de segunda ordem, existe outro gene "zero" - o 512. Vamos ver como esse gene afeta o fenótipo.Os genes 0 e 512 são sempre zero: o
nas máquinas de segunda ordem, existe outro gene "zero" - o 512. Vamos ver como esse gene afeta o fenótipo.Os genes 0 e 512 são sempre zero: o gene 0 é sempre zero. O 512º gene é sempre igual a um:
gene 0 é sempre zero. O 512º gene é sempre igual a um: para não zombar de nossos estimados epiléticos, mais uma vez, o 0º e o 512º serão preenchidos com zeros na população inicial do algoritmo genético.Vejamos as máquinas das quais nos livramos, definindo zeros nos genes 0 e 512.Os oito primeiros estados de um autômato no qual apenas o 0º gene é preenchido (o gene zero é um, o resto são zeros): um
para não zombar de nossos estimados epiléticos, mais uma vez, o 0º e o 512º serão preenchidos com zeros na população inicial do algoritmo genético.Vejamos as máquinas das quais nos livramos, definindo zeros nos genes 0 e 512.Os oito primeiros estados de um autômato no qual apenas o 0º gene é preenchido (o gene zero é um, o resto são zeros): um autômato no qual apenas o 512º gene
autômato no qual apenas o 512º gene é preenchido : um autômato no qual apenas o 0º e o 512º genes são preenchidos:
é preenchido : um autômato no qual apenas o 0º e o 512º genes são preenchidos: Vamos destacar um lugar no gráfico em que a população começa a se dividir em grupos:
Vamos destacar um lugar no gráfico em que a população começa a se dividir em grupos: nesse local, os genótipos são preenchidos em 25%.Compare duas populações.Primeira população. 30 máquinas aleatórias na 1000ª iteração. Os genótipos estão 50% completos (512 unidades e 512 zeros):
nesse local, os genótipos são preenchidos em 25%.Compare duas populações.Primeira população. 30 máquinas aleatórias na 1000ª iteração. Os genótipos estão 50% completos (512 unidades e 512 zeros): a segunda população. 30 máquinas aleatórias na 1000ª iteração. Os genótipos estão 25% cheios (256 unidades e 768 zeros):
a segunda população. 30 máquinas aleatórias na 1000ª iteração. Os genótipos estão 25% cheios (256 unidades e 768 zeros): a segunda população é adequada para seleção artificial. Podemos destacar facilmente alguns dos sinais nessas máquinas. Por exemplo: “mais escuro”, “menos caótico” (autômatos nos quais os glóbulos brancos estão agrupados), etc.Nós selecionamos "mais escuro". A probabilidade de mutações é de 10%, até 4 genes se mutam. Após a primeira seleção:
a segunda população é adequada para seleção artificial. Podemos destacar facilmente alguns dos sinais nessas máquinas. Por exemplo: “mais escuro”, “menos caótico” (autômatos nos quais os glóbulos brancos estão agrupados), etc.Nós selecionamos "mais escuro". A probabilidade de mutações é de 10%, até 4 genes se mutam. Após a primeira seleção: Após a segunda seleção:
Após a segunda seleção: Um autômato interessante apareceu na população.256x256, estado da máquina na 1000ª iteração: a
Um autômato interessante apareceu na população.256x256, estado da máquina na 1000ª iteração: a máquina preenche gradualmente a população.Após a oitava seleção:
máquina preenche gradualmente a população.Após a oitava seleção: Outra máquina interessante apareceu.256x256, estado do autômato na 1000ª iteração:
Outra máquina interessante apareceu.256x256, estado do autômato na 1000ª iteração: População após treze seleções:
População após treze seleções: Vários autômatos dessa população. 256x256, 1000ª iteração para todos. Abaixo da imagem, há um link, clicando no qual você pode ver a máquina na dinâmica:
Vários autômatos dessa população. 256x256, 1000ª iteração para todos. Abaixo da imagem, há um link, clicando no qual você pode ver a máquina na dinâmica: Visualizar na dinâmica.
Visualizar na dinâmica. Ver em dinâmica.
Ver em dinâmica. Ver em dinâmica.
Ver em dinâmica. Ver em dinâmica.
Ver em dinâmica. Ver em dinâmica.
Ver em dinâmica. Ver em dinâmica.
Ver em dinâmica. Ver em dinâmica.
Ver em dinâmica. Ver em dinâmica.
Ver em dinâmica. Ver em dinâmica.
Ver em dinâmica. Ver em dinâmica.
Ver em dinâmica.3. Máquina automática Conway e similares
O mais famoso autômato celular bidimensional de primeira ordem é o jogo de autômatos Conway "Life" .As regras para o autômato de Conway são escritas da seguinte forma:Se houver 3 células vivas em torno de uma célula morta, a célula ganha vida (caso contrário, permanece morta).Se houver 2 ou 3 células vivas em torno de uma célula viva, a célula permanece viva (caso contrário, ela morre).Uma célula morta é 0, uma célula viva é 1.Cerca de uma célula pode ter de 0 a 8 células vivas. De acordo com 9 opções em torno dos vivos e em torno da célula morta. Escrevemos todas as opções para a matriz r:matriz r r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ];
A primeira metade da matriz é para uma célula morta, a segunda para uma célula viva.Podemos descrever a regra do autômato de Conway para todas as combinações possíveis (512) de uma célula e 8 células vizinhas:Pinte a regra r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; var q1, q2; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[1]+1*ii[2]+1*ii[3]+1*ii[5]+1*ii[6]+1*ii[7]+1*ii[8]; if(q1==0) rule[i]=r[q2]; else rule[i]=r[q2+9]; }
Opção otimizada r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; for(var i=0;i<512;i++){ var q=((i>>4)&1)*8; for(var j=0;j<9;j++){ q+=(i>>j)&1; } rule[i]=r[q]; }
Para um autômato de segunda ordem, copie a segunda metade da matriz de regras da primeira:Copiar for(var i=0;i<512;i++){ if(rule[i]==0) rule[i+512]=0; else rule[i+512]=1; }
Iniciamos a máquina com a regra especificada. Vemos os planadores e osciladores característicos. Várias iterações desse autômato: A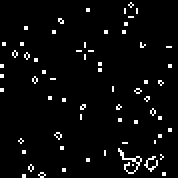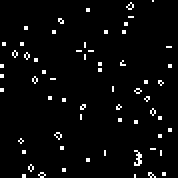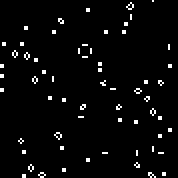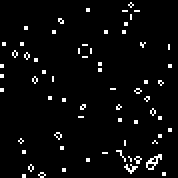 matriz r consiste em 18 células. Existe2 18 = 262144 autômatos semelhantes ao autômato de Conway (que podem ser escritos pelas mesmas regras: o número de células vivas cercadas pelos mortos, em que a célula ganha vida e o número de células vivas no ambiente em que a célula morre).Você pode vê-losaqui(por padrão, o autômato Conway é iniciado, o botão "Alterar regra" preenche a matriz r aleatoriamente).Múltiplas máquinas aleatórias (código binário - matriz r):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111 000001100110111111
matriz r consiste em 18 células. Existe2 18 = 262144 autômatos semelhantes ao autômato de Conway (que podem ser escritos pelas mesmas regras: o número de células vivas cercadas pelos mortos, em que a célula ganha vida e o número de células vivas no ambiente em que a célula morre).Você pode vê-losaqui(por padrão, o autômato Conway é iniciado, o botão "Alterar regra" preenche a matriz r aleatoriamente).Múltiplas máquinas aleatórias (código binário - matriz r):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111 000001100110111111





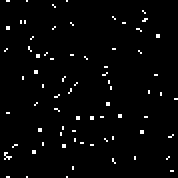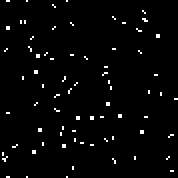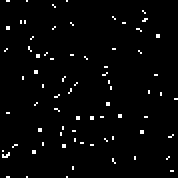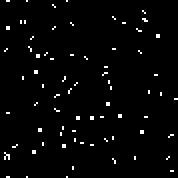

 Para um algoritmo genético, como genótipo, você pode usar como um array r ( 2 18 combinações) e a matriz de regras (2 512 combinações de primeira ordem para o autómato e celular2 1024 - para um autômato celular de segunda ordem).2 18 é um número relativamente pequeno. Esse número permite que você selecione a regra da máquina manualmente, sem usar um algoritmo genético (de fato, o que Conway fez). Se você preencher a matriz de regras com máquinas aleatórias desse tipo e usar essa matriz como um genótipo, o experimento poderá ser considerado sem êxito, até certo ponto (o suficiente para não mostrar os resultados desse experimento no artigo). Nas regras de autômatos celulares desse tipo, há simetria. Por exemplo, para as seguintes combinações de células:
Para um algoritmo genético, como genótipo, você pode usar como um array r ( 2 18 combinações) e a matriz de regras (2 512 combinações de primeira ordem para o autómato e celular2 1024 - para um autômato celular de segunda ordem).2 18 é um número relativamente pequeno. Esse número permite que você selecione a regra da máquina manualmente, sem usar um algoritmo genético (de fato, o que Conway fez). Se você preencher a matriz de regras com máquinas aleatórias desse tipo e usar essa matriz como um genótipo, o experimento poderá ser considerado sem êxito, até certo ponto (o suficiente para não mostrar os resultados desse experimento no artigo). Nas regras de autômatos celulares desse tipo, há simetria. Por exemplo, para as seguintes combinações de células: o estado da célula na próxima iteração é o mesmo. Após a primeira travessia, a simetria nas regras dos indivíduos descendentes é quebrada. Indivíduos ancestrais acumulam mutações que também destroem a simetria. A violação da simetria no genótipo causa uma violação da simetria no fenótipo.Pode-se ver a manifestação dessa simetria no fenótipo se uma célula for preenchida no estado inicial do autômato.Vamos fazer um experimento. Para manter a simetria, usaremos a matriz r como um genótipo. Mutações de 5%, 1 gene mutado. No estado inicial, uma célula é preenchida.30 máquinas aleatórias da população inicial. O estado dos autômatos na 30ª iteração:
o estado da célula na próxima iteração é o mesmo. Após a primeira travessia, a simetria nas regras dos indivíduos descendentes é quebrada. Indivíduos ancestrais acumulam mutações que também destroem a simetria. A violação da simetria no genótipo causa uma violação da simetria no fenótipo.Pode-se ver a manifestação dessa simetria no fenótipo se uma célula for preenchida no estado inicial do autômato.Vamos fazer um experimento. Para manter a simetria, usaremos a matriz r como um genótipo. Mutações de 5%, 1 gene mutado. No estado inicial, uma célula é preenchida.30 máquinas aleatórias da população inicial. O estado dos autômatos na 30ª iteração: Vamos tentar isolar esses autômatos que se desenvolvem (crescem) mais lentamente a partir de uma célula.
Vamos tentar isolar esses autômatos que se desenvolvem (crescem) mais lentamente a partir de uma célula.



 Após a primeira seleção, eles se livraram de autômatos que não se desenvolvem:
Após a primeira seleção, eles se livraram de autômatos que não se desenvolvem: Na nova população, existem vários desses autômatos (que não se desenvolvem) - estes são descendentes e mutantes sem êxito.Em seguida, selecionaremos principalmente máquinas com fundo branco (células nas quais a máquina não foi desenvolvida).
Na nova população, existem vários desses autômatos (que não se desenvolvem) - estes são descendentes e mutantes sem êxito.Em seguida, selecionaremos principalmente máquinas com fundo branco (células nas quais a máquina não foi desenvolvida).Máquinas de venda automática pretas piscam.( — ) — . ( ) ( ). . — () . ( — , — ). 30- , — . ( 30- ) — ( ).
População após a segunda seleção: 3 seleções:
3 seleções: 5 seleções:
5 seleções: 8 seleções:
8 seleções: 13 seleções:
13 seleções: As mesmas máquinas na 60ª iteração:
As mesmas máquinas na 60ª iteração: 21 seleções. O estado dos autômatos na 30ª iteração: O
21 seleções. O estado dos autômatos na 30ª iteração: O estado dos autômatos na 60ª iteração:
estado dos autômatos na 60ª iteração: 34 seleções. Estado de autômatos na 30ª iteração:
34 seleções. Estado de autômatos na 30ª iteração: Estado de autômatos na 60ª iteração:
Estado de autômatos na 60ª iteração: Além disso, o sistema não evolui. Três autômatos dessa população (100 iteraçõescada ): [1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1]
Além disso, o sistema não evolui. Três autômatos dessa população (100 iteraçõescada ): [1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1] [1 0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1]
[1 0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1] [1,0,0,1,1,0,0, 1,1,0,1,0,1,1,0,1,1,1]
[1,0,0,1,1,0,0, 1,1,0,1,0,1,1,0,1,1,1] Para comparação, uma máquina aleatória:[1,0,0,1,1,1,0,1,1,1,0, 0,1,1,0,0,0,1]
Para comparação, uma máquina aleatória:[1,0,0,1,1,1,0,1,1,1,0, 0,1,1,0,0,0,1]
4. Autômato de Conway e similares (2)
Em máquinas com as regras do tipo Conway, contamos o número de unidades vivas de células nas proximidades de Moore. Essa vizinhança pode ser dividida em 4 pares e contar o número de células vivas nesses pares: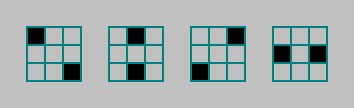 Assim, aumentamos o número de autômatos, mas mantemos a simetria no fenótipo.Cada par pode ter de 0 a 2 células vivas. Par 4. Número de combinações3 4 = 81
Assim, aumentamos o número de autômatos, mas mantemos a simetria no fenótipo.Cada par pode ter de 0 a 2 células vivas. Par 4. Número de combinações3 4 = 81 .
De acordo com a 81ª combinação em torno da célula viva e em torno da célula morta. Total existe2 162 máquinas automáticas deste tipo. Número:2 162 ≈ 5.846 × 10 48
É completamente astronômico e será adequado para um algoritmo genético.O tamanho do genótipo de cada indivíduo é de 162 genes:Encha a população com máquinas aleatórias var rulesize=162; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }
Em seguida, pintamos essa regra para todas as combinações possíveis de uma célula e oito células vizinhas:Função fillrule (); function fillrule(){ var r; for(var n=0;n<PopulationSize;n++){ rule[n]=[]; r=population[n]; var q1, q2, q3, q4, q5; var q; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[8]; q3=1*ii[1]+1*ii[7]; q4=1*ii[2]+1*ii[6]; q5=1*ii[3]+1*ii[5]; q=parseInt(''+q2+q3+q4+q5,3); if(q1==0) rule[n][i]=r[q]; else rule[n][i]=r[q+81]; } } }
Usaremos a matriz de regras ao calcular o próximo estado do autômato. Chamamos a função fillrule () depois de carregar a página e depois de chamar a função evolute ().A população inicial parece caótica. 30 máquinas aleatórias, 1000ª iteração: Esse caos varia levemente em dinâmica e as máquinas são bastante adequadas para a seleção, mas vamos facilitar: escolheremos as "mais sombrias".População após cinco seleções:
Esse caos varia levemente em dinâmica e as máquinas são bastante adequadas para a seleção, mas vamos facilitar: escolheremos as "mais sombrias".População após cinco seleções: Em seguida, você pode procurar máquinas com os osciladores mais complexos. Todo o processo de disposição é inútil. Abaixo estão alguns dos autômatos mais interessantes encontrados usando o algoritmo genético.256x256, 10000ª iteração para todos. Abaixo da imagem, há um link, clicando no qual você pode ver a máquina na dinâmica:
Em seguida, você pode procurar máquinas com os osciladores mais complexos. Todo o processo de disposição é inútil. Abaixo estão alguns dos autômatos mais interessantes encontrados usando o algoritmo genético.256x256, 10000ª iteração para todos. Abaixo da imagem, há um link, clicando no qual você pode ver a máquina na dinâmica: Visualizar na dinâmica.
Visualizar na dinâmica. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.?
E você pode brincar por aqui:autômatos celulares bidimensionais de segunda ordem.Interface: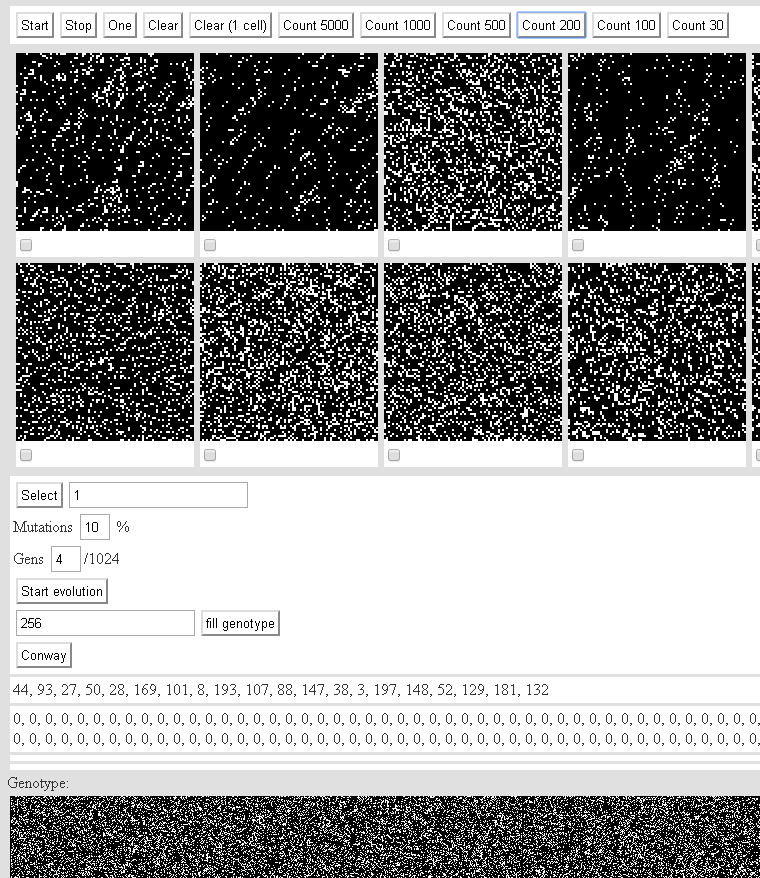 O botão Iniciar inicia as máquinas.Stop - para.Um é uma iteração.Limpar - para a máquina e preenche o estado inicial de forma aleatória.Limpar (1 célula) - para a máquina e preenche uma célula no estado inicial.Os botões restantes nesta linha contam o número especificado de iterações para cada autômato.A renderização de um autômato na tela consome todo o desempenho. Se você precisar calcular rapidamente 200 iterações, clique em Count 200. Não clicamos no botão Count 5000 - o navegador pode travá-lo.Abaixo de 20 máquinas aleatórias (tamanho da população - 200 máquinas). Nas caixas de seleção das máquinas de venda automática. Marcamos o mais interessante. Pressione Selecionar - a adequação da máquina aumentará pelo número indicado à direita.Mutações - a probabilidade de mutações.Gens é o número de genes mutantes.Iniciar evolução - lança o mecanismo de cruzamentos e mutações.Preencher genótipo - preenche o número especificado de genes no genótipo de cada autômato.Conway - enche a população com máquinas do tipo Konveevsky.Abaixo estão duas linhas: Osnúmeros das máquinas mostradas.O conteúdo da matriz fenótipo.O pool genético da população é ainda menor.Todo o progresso é armazenado no armazenamento local.Você pode jogar com as espingardas de assalto do tipo Konveevsky (com as que foram consideradas por último no artigo) aqui:4. Autômato Conway e similares (2).
O botão Iniciar inicia as máquinas.Stop - para.Um é uma iteração.Limpar - para a máquina e preenche o estado inicial de forma aleatória.Limpar (1 célula) - para a máquina e preenche uma célula no estado inicial.Os botões restantes nesta linha contam o número especificado de iterações para cada autômato.A renderização de um autômato na tela consome todo o desempenho. Se você precisar calcular rapidamente 200 iterações, clique em Count 200. Não clicamos no botão Count 5000 - o navegador pode travá-lo.Abaixo de 20 máquinas aleatórias (tamanho da população - 200 máquinas). Nas caixas de seleção das máquinas de venda automática. Marcamos o mais interessante. Pressione Selecionar - a adequação da máquina aumentará pelo número indicado à direita.Mutações - a probabilidade de mutações.Gens é o número de genes mutantes.Iniciar evolução - lança o mecanismo de cruzamentos e mutações.Preencher genótipo - preenche o número especificado de genes no genótipo de cada autômato.Conway - enche a população com máquinas do tipo Konveevsky.Abaixo estão duas linhas: Osnúmeros das máquinas mostradas.O conteúdo da matriz fenótipo.O pool genético da população é ainda menor.Todo o progresso é armazenado no armazenamento local.Você pode jogar com as espingardas de assalto do tipo Konveevsky (com as que foram consideradas por último no artigo) aqui:4. Autômato Conway e similares (2).