O trabalho de pesquisa é talvez a parte mais interessante do nosso treinamento. A idéia é tentar-se na direção escolhida, mesmo na universidade. Por exemplo, estudantes de Engenharia de Software e Machine Learning costumam fazer pesquisas na empresa (principalmente JetBrains ou Yandex, mas não apenas).
Neste post vou falar sobre o meu projeto em Ciência da Computação. Como parte do trabalho, estudei e coloquei em prática abordagens para solucionar um dos problemas mais difíceis de NP-difícil:
o problema de cobertura de vértices .
Agora, uma abordagem interessante para problemas difíceis de NP está desenvolvendo rapidamente algoritmos parametrizados. Vou tentar atualizar você, contar alguns algoritmos parametrizados simples e descrever um método poderoso que me ajudou muito. Apresentei meus resultados no PACE Challenge: de acordo com os resultados dos testes abertos, minha decisão ocupa o terceiro lugar e os resultados finais serão conhecidos em 1º de julho.

Sobre mim
Meu nome é Vasily Alferov, agora estou completando o terceiro ano do HSE - São Petersburgo. Eu gosto de algoritmos desde os tempos escolares, quando estudei na escola de Moscou 179 e participei com sucesso de competições de ciência da computação.
O número final de especialistas em algoritmos parametrizados vai para o bar ...
Um exemplo é retirado do livro "Algoritmos parametrizados"Imagine que você é um guarda de bar em uma cidade pequena. Toda sexta-feira, metade da cidade vem ao seu bar para relaxar, o que gera muitos problemas: você precisa expulsar visitantes violentos do bar para evitar brigas. No final, isso incomoda você e você decide tomar medidas preventivas.
Como sua cidade é pequena, você tem certeza de que pares de visitantes provavelmente trarão brigas se chegarem ao bar juntos. Você tem uma lista de
n pessoas que irão ao bar hoje à noite. Você decide não deixar nenhuma cidade entrar no bar para que ninguém lute. Ao mesmo tempo, seus superiores não querem perder lucros e ficarão infelizes se você não deixar mais que
k pessoas irem ao bar.
Infelizmente, o desafio que você está enfrentando é uma tarefa clássica difícil de NP. Você poderia conhecê-lo como
cobertura de vértice ou como um problema de cobertura de vértice. Para tais problemas, no caso geral, os algoritmos que funcionam em um tempo aceitável são desconhecidos. Para ser preciso, a hipótese não comprovada e bastante forte ETH (Hipótese de Tempo Exponencial) diz que esse problema não pode ser resolvido a tempo
, isto é, o que é visivelmente melhor do que a pesquisa exaustiva não pode ser pensado. Por exemplo, permita que
n = 1000 pessoas planejem ir ao seu bar. Em seguida, uma pesquisa completa será
opções que existem aproximadamente
- insanamente demais. Felizmente, seu guia define um limite de
k = 10 ; portanto, o número de combinações que você precisa repetir é muito menor: o número de subconjuntos de dez elementos é
. Isso já é melhor, mas ainda não conta para o dia, mesmo em um cluster poderoso.
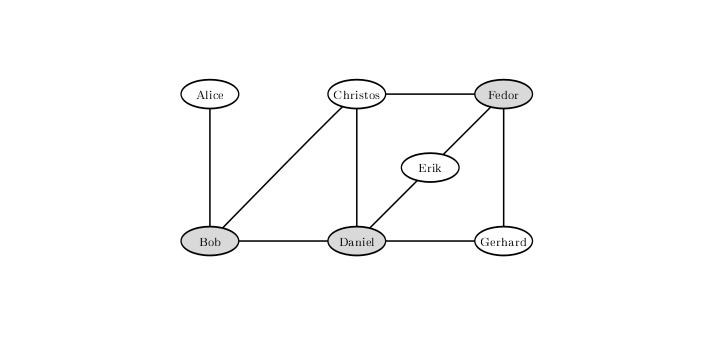
Para excluir a possibilidade de uma briga com essa configuração de relações tensas entre os visitantes do bar, você não deve deixar Bob, Daniel e Fedor. Uma solução na qual apenas duas são deixadas ao mar não existe.
Isso significa que é hora de se render e deixar todo mundo entrar? Vamos considerar outras opções. Bem, por exemplo, você não pode deixar entrar apenas aqueles que provavelmente lutarão com um número muito grande de pessoas. Se alguém pode lutar com pelo menos
k + 1 por outra pessoa, então você definitivamente não pode deixá-lo entrar, caso contrário você terá que não deixar todos os
k + 1 habitantes da cidade com quem ele pode lutar, o que definitivamente perturbará a liderança.
Que você jogue fora tudo o que pôde de acordo com esse princípio. Então todo mundo pode lutar com não mais que
k pessoas. Jogando
k pessoas fora deles, você pode evitar não mais do que
conflitos. Então, se tudo mais do que
se uma pessoa estiver envolvida em pelo menos um conflito, você certamente não poderá impedir todas. Como é claro que você tem certeza de deixar as pessoas completamente sem conflito irem, é necessário separar todos os subconjuntos do tamanho de dez entre duzentas pessoas. Existem aproximadamente
, e muitas operações já podem ser classificadas no cluster.
Se é seguro ter personalidades completamente não conflitantes, o que dizer daqueles que estão envolvidos em apenas um conflito? De fato, eles também podem entrar fechando as portas na frente do oponente. De fato, se Alice entrar em conflito apenas com Bob, se deixarmos dois entrarem em Alice, não perderemos: Bob pode ter outros conflitos, mas Alice definitivamente não os possui. Além disso, não faz sentido para nós não deixar os dois. Após essas operações, não haverá mais
convidados com um destino não resolvido: tudo o que temos
conflitos, em cada um dos dois participantes e cada um envolvido em pelo menos dois. Então, resta apenas resolver
opções, que podem ser calculadas por meio dia em um laptop.
De fato, o raciocínio simples pode alcançar condições ainda mais atraentes. Observe que, definitivamente, precisamos resolver todas as disputas, ou seja, de cada par conflitante para escolher pelo menos uma pessoa a quem não deixaremos entrar. Considere este algoritmo: pegue qualquer conflito do qual excluamos um participante e iniciemos recursivamente do restante, depois exclua outro e também inicie recursivamente. Como lançamos alguém a cada passo, a árvore de recursão de um algoritmo é uma árvore binária de profundidade
k , portanto, no total, o algoritmo funciona para
onde
n é o número de vértices e
m é o número de arestas. No nosso exemplo, são cerca de dez milhões, que em uma fração de segundo serão contados não apenas em um laptop, mas também em um telefone móvel.
O exemplo acima é um exemplo de um
algoritmo parametrizado . Algoritmos parametrizados são algoritmos que funcionam durante
f (k) poli (n) , onde
p é um polinômio,
f é uma função computável arbitrária e
k é um parâmetro que, possivelmente, será muito menor que o tamanho do problema.
Todas as discussões anteriores a esse algoritmo fornecem um exemplo de
kernelização , uma das técnicas comuns para a criação de algoritmos parametrizados. Kernelization é uma redução no tamanho de uma tarefa para um valor limitado pela função de um parâmetro. A tarefa resultante é frequentemente chamada de kernel. Assim, pelo simples raciocínio sobre graus de vértices, obtivemos um núcleo quadrático para o problema Vertex Cover, parametrizado pelo tamanho da resposta. Existem outros parâmetros que podem ser selecionados para esta tarefa (por exemplo, Vertex Cover Above LP), mas discutiremos exatamente esse parâmetro.
Desafio de ritmo
O concurso
PACE Challenge (
Desafio de algoritmos parametrizados e experimentos computacionais) começou em 2015 para estabelecer uma conexão entre algoritmos parametrizados e abordagens usadas na prática para resolver problemas computacionais. As três primeiras competições foram dedicadas a encontrar a largura da árvore do gráfico (largura da árvore), encontrar a
árvore Steiner (
árvore Steiner ) e encontrar muitos vértices, ciclos de corte (
Feedback Vertex Set ). Este ano, uma das tarefas em que alguém poderia tentar os pontos fortes foi o problema da cobertura descrita acima.
A concorrência está ganhando popularidade a cada ano. Se você acredita nos dados preliminares, este ano apenas 24 equipes participaram da competição para resolver o problema da cobertura de vértices. Vale ressaltar que a competição não dura várias horas e nem uma semana, mas vários meses. As equipes têm a oportunidade de estudar literatura, apresentar sua ideia original e tentar implementá-la. De fato, esta competição é um trabalho de pesquisa. As idéias para as soluções mais eficazes e a premiação dos vencedores serão realizadas em conjunto com a conferência do
IPEC (Simpósio Internacional de Computação Parametrizada e Exata) na maior reunião algorítmica anual da Europa
ALGO . Mais informações sobre a competição em si podem ser encontradas no
site , e os resultados dos últimos anos estão
aqui .
Esquema de solução
Para lidar com o problema da cobertura de vértices, tentei aplicar algoritmos parametrizados. Eles geralmente consistem em duas partes: regras de simplificação (que idealmente levam à kernelização) e regras de divisão. As regras de simplificação estão pré-processando a entrada em tempo polinomial. O objetivo de aplicar essas regras é reduzir o problema a um problema equivalente de tamanho menor. As regras de simplificação são a parte mais cara do algoritmo, e a aplicação dessa parte específica leva ao tempo total de trabalho
em vez de um tempo polinomial simples. No nosso caso, as regras de divisão são baseadas no fato de que, para cada vértice, é necessário levar o vizinho em resposta.
O esquema geral é o seguinte: aplicamos as regras de simplificação, depois selecionamos algum vértice e fazemos duas chamadas recursivas: no primeiro, o respondemos e, no outro, todos os vizinhos. Isso é o que chamamos de divisão (brunching) ao longo deste pico.
Exatamente uma adição será feita a esse esquema no próximo parágrafo.
Ideias para dividir regras
Vamos discutir como escolher um vértice ao longo do qual a divisão ocorrerá.
A idéia principal é muito gananciosa no sentido algorítmico: vamos pegar o pico do grau máximo e dividi-lo por ele. Por que parece tão melhor? Como no segundo ramo da chamada recursiva, removeremos muitos vértices dessa maneira. Você pode esperar que um pequeno gráfico permaneça e iremos trabalhar rapidamente.
Essa abordagem, com as técnicas simples de kernelization já discutidas, não é ruim, resolve alguns testes com um tamanho de vários milhares de vértices. Mas, por exemplo, ele não funciona bem para gráficos cúbicos (ou seja, gráficos cujo grau de cada vértice é três).
Há outra idéia baseada em uma idéia bastante simples: se o gráfico for desconectado, o problema em seus componentes conectados poderá ser resolvido independentemente, combinando as respostas no final. A propósito, essa é a pequena modificação prometida no esquema, que acelerará significativamente a solução: anteriormente, neste caso, trabalhamos para o produto dos tempos de contagem das respostas dos componentes e agora trabalhamos pela quantia. E para acelerar o brunching, você precisa transformar um gráfico conectado em um gráfico desconectado.
Como fazer isso? Se houver um ponto de articulação no gráfico, é necessário passear por ele. Um ponto de articulação é um vértice que, quando removido, o gráfico perde a conectividade. Encontre no gráfico todos os pontos da junta que podem ser um algoritmo clássico em tempo linear. Essa abordagem acelera significativamente o brunch.
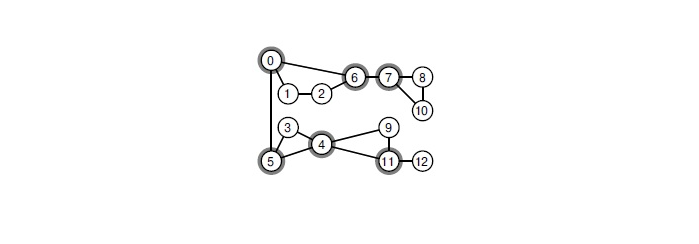
Quando você remove qualquer um dos vértices selecionados, o gráfico se decompõe em componentes conectados.
Vamos fazer isso, mas eu quero mais. Por exemplo, procure por pequenas seções de vértices no gráfico e divida ao longo dos vértices a partir dele. A maneira mais eficaz de encontrar a seção mínima global de vértices é usar a árvore Gomori-Hu, construída em tempo cúbico. No Desafio PACE, um tamanho típico de gráfico é de vários milhares de vértices. Nesse cenário, bilhões de operações precisam ser executadas em cada vértice da árvore de recursão. Acontece que é simplesmente impossível resolver o problema no tempo previsto.
Vamos tentar otimizar a solução. A seção mínima de vértice entre um par de vértices pode ser encontrada por qualquer algoritmo que construa o fluxo máximo. Você pode executar o
algoritmo Dinitz em uma rede desse tipo; na prática, ele funciona muito rapidamente. Suspeito que teoricamente seja possível provar uma estimativa para o tempo de trabalho
isso já é bastante aceitável.
Tentei várias vezes procurar cortes entre pares de vértices aleatórios e pegar o mais equilibrado deles. Infelizmente, nos testes abertos do Desafio PACE, isso deu resultados ruins. Comparei-o com um algoritmo disperso ao longo dos vértices do grau máximo, iniciando-os com uma restrição na profundidade da descida. Depois que o algoritmo tentou encontrar o corte dessa maneira, restaram gráficos maiores. Isso se deve ao fato de os cortes terem sido muito desequilibrados: após a remoção de 5 a 10 vértices, apenas 15 a 20 foram capazes de ser separados.
Vale a pena notar que artigos sobre os algoritmos mais rápidos teoricamente usam técnicas muito mais avançadas para selecionar vértices para divisão. Tais técnicas têm uma implementação muito complexa e, muitas vezes, graus ruins de tempo e memória. Eu não conseguia distinguir deles bastante aceitável para a prática.
Como aplicar regras de simplificação
Já temos idéias para kernelização. Deixe-me lembrá-lo:
- Se houver um vértice isolado, exclua-o.
- Se houver um vértice de grau 1, exclua-o e aceite seu vizinho em resposta.
- Se houver um vértice de grau pelo menos k + 1 , aceite-o em resposta.
Nos dois primeiros, tudo fica claro; no terceiro, há um truque. Se no problema da barra de quadrinhos recebemos uma restrição de cima em
k , no Desafio PACE, você só precisa encontrar a cobertura de vértice do tamanho mínimo. Essa é uma transformação típica de um problema de pesquisa em um problema de decisão, geralmente entre os dois tipos de tarefas que eles não fazem diferença. Na prática, se escrevermos um solucionador de problemas de cobertura de vértices, pode haver uma diferença. Por exemplo, como no terceiro parágrafo.
Em termos de implementação, existem duas maneiras de fazer isso. A primeira abordagem é chamada Aprofundamento Iterativo. Consiste no seguinte: podemos começar com alguma restrição razoável de baixo na resposta e executar nosso algoritmo, usando essa restrição como uma restrição na resposta de cima, sem diminuir a recursão abaixo dessa restrição. Se encontrarmos alguma resposta, a garantia é ótima, caso contrário, você poderá aumentar esse limite em um e começar de novo.
Outra abordagem é armazenar uma resposta ótima atual e procurar uma resposta menor, quando encontrada, altere esse parâmetro
k para eliminar mais os ramos em excesso na pesquisa.
Depois de realizar várias experiências noturnas, decidi por uma combinação desses dois métodos: primeiro executo meu algoritmo com algum tipo de restrição na profundidade da pesquisa (escolhendo-o para levar um tempo insignificante em comparação com a solução principal) e use a melhor solução encontrada como restrição acima. para a resposta - isto é, para esse mesmo
k .
Vértices de grau 2
Com vértices de graus 0 e 1, descobrimos. Acontece que isso também pode ser feito com vértices de grau 2, mas, para isso, o gráfico exigirá operações mais complexas.
Para explicar isso, você precisa identificar de alguma forma os picos. Chamamos um vértice de grau 2 o vértice
v , e seus vizinhos os vértices
x e
y . Então teremos dois casos.
- Quando x e y são vizinhos. Em seguida, você pode receber a resposta xey , e excluir v . De fato, pelo menos dois vértices devem ser retirados desse triângulo em resposta e certamente não perderemos se tomarmos xey : eles provavelmente têm mais vizinhos, mas v não.
- Quando x e y não são vizinhos. Então, afirma-se que todos os três vértices podem ser colados em um. A idéia é que, neste caso, exista uma resposta ótima na qual pegamos v ou ambos os vértices x e y . Além disso, no primeiro caso, temos de responder a todos os vizinhos xey , e no segundo não é necessário. Este é exatamente o caso quando não pegamos o vértice colado em resposta e quando o pegamos. Resta apenas observar que, em ambos os casos, a resposta dessa operação diminui em um.
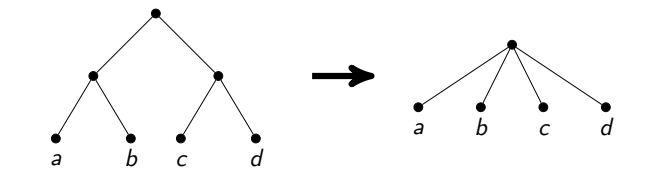
Vale a pena notar que tal abordagem para um tempo linear honesto é bastante difícil de implementar com precisão. A colagem de vértices é uma operação difícil, você precisa copiar as listas de vizinhos. Se você fizer isso de forma descuidada, poderá obter um tempo de operação assintoticamente não ideal (por exemplo, se você copiar muitas arestas após cada colagem). Decidi procurar caminhos inteiros a partir de vértices de grau 2 e analisar vários casos especiais, como loops desses vértices ou de todos esses vértices, exceto um.
Além disso, é necessário que esta operação seja reversível, para que, durante o retorno da recursão, restauremos o gráfico em sua forma original. Para garantir isso, não limpei as listas de arestas dos vértices mesclados, após o que sabia apenas para quais arestas deveriam ser direcionadas. Essa implementação de gráficos também requer precisão, mas fornece um tempo linear honesto. E para gráficos de várias dezenas de milhares de arestas, ele se encaixa completamente no cache do processador, o que oferece grandes vantagens de velocidade.
Núcleo linear
Finalmente, a parte mais interessante do kernel.
Primeiro, lembre-se de que, em gráficos bipartidos, a cobertura mínima de vértices pode ser procurada para
. Para fazer isso, use o algoritmo
Hopcroft-Karp para encontrar a correspondência máxima lá e, em seguida, use o teorema de
Koenig-Egerwari .
A idéia de um núcleo linear é a seguinte: primeiro dividimos o gráfico, ou seja, em vez de cada vértice
v, obtemos dois vértices
e
, e em vez de cada aresta
u - v , temos duas arestas
e
. O gráfico resultante será bipartido. Encontramos nele a cobertura mínima de vértices. Alguns vértices do gráfico original chegam lá duas vezes, outros apenas uma vez e outros nunca. O teorema de Nemhauser-Trotter afirma que, neste caso, é possível remover vértices que não foram atingidos uma vez e responder aos que atingiram duas vezes. Além disso, ela diz que, dos picos restantes (aqueles que atingiram uma vez), você precisa voltar pelo menos pela metade.
Acabamos de aprender a deixar não mais que
2 mil vértices em um gráfico. De fato, se o restante da resposta for pelo menos metade de todos os vértices, então o total de vértices não terá mais que
2k .
Aqui consegui dar um pequeno passo adiante. É claro que o kernel construído dessa maneira depende de que tipo de cobertura mínima de vértices no gráfico bipartido que usamos. Gostaria de considerar que o número de vértices restantes seja mínimo. Anteriormente, eles só sabiam como fazê-lo a tempo.
. Eu vim com a implementação deste algoritmo a tempo
Assim, esse núcleo pode ser pesquisado em gráficos de centenas de milhares de vértices em cada estágio da ramificação.
Resultado
A prática mostra que minha solução funciona bem em testes de várias centenas de vértices e milhares de arestas. Em tais testes, pode-se esperar que uma solução seja encontrada em meia hora. A probabilidade de encontrar uma resposta em um período aceitável aumenta em princípio se o gráfico tiver muitos vértices de alto grau, por exemplo, graus 10 e acima.
Para participar da competição, as decisões tiveram que ser enviadas para o
optil.io . A julgar pelo
prato apresentado lá, minha decisão em testes abertos ocupa a terceira de vinte, com uma ampla margem a partir da segunda. Para ser completamente honesto, não está totalmente claro como as decisões serão avaliadas na própria competição: por exemplo, minha decisão passa em menos testes do que a decisão em quarto lugar, mas funciona mais rápido para aqueles que passam.
Os resultados dos testes fechados serão anunciados em 1º de julho.