Bem-vindo a uma das palestras em CS231n: Redes neurais convolucionais para reconhecimento visual .

Conteúdo

• Visão geral da arquitetura
• Camadas em uma rede neural convolucional
  - camada convolucional
  - Subamostragem de camada
  - Camada de normalização
  - camada totalmente conectada
  - Converta camadas totalmente conectadas em camadas convolucionais
• Arquitetura de rede neural convolucional
  - Modelos de camada
  - Padrões de tamanho de camada
  - Estudo de caso (LeNet, AlexNet, ZFNet, GoogLeNet, VGGNet)
  - Aspectos computacionais
• Leitura adicional

Redes neurais convolucionais (CNN / ConvNets)

As redes neurais convolucionais são muito semelhantes às redes neurais usuais que estudamos no capítulo anterior (referindo-se ao capítulo anterior do curso CS231n): elas consistem em neurônios que, por sua vez, contêm pesos e deslocamentos variáveis. Cada neurônio recebe alguns dados de entrada, calcula o produto escalar e, opcionalmente, usa uma função de ativação não linear. Toda a rede, como antes, é a única função de avaliação diferenciável: do conjunto inicial de pixels (imagem) em uma extremidade à distribuição de probabilidade de pertencer a uma classe específica na outra extremidade. Essas redes ainda têm uma função de perda (por exemplo, SVM / Softmax) na última camada (totalmente conectada), e todas as dicas e recomendações fornecidas no capítulo anterior sobre redes neurais comuns também são relevantes para redes neurais convolucionais.

Então o que mudou? A arquitetura das redes neurais convolucionais envolve explicitamente a obtenção de imagens na entrada, o que nos permite levar em consideração certas propriedades dos dados de entrada na própria arquitetura de rede. Essas propriedades permitem implementar a função de distribuição direta com mais eficiência e reduzir bastante o número total de parâmetros na rede.

Visão geral da arquitetura

Recordamos redes neurais comuns. Como vimos no capítulo anterior, as redes neurais recebem dados de entrada (um único vetor) e os transformam "empurrando" através de uma série de camadas ocultas . Cada camada oculta consiste em um certo número de neurônios, cada um dos quais está conectado a todos os neurônios da camada anterior e onde os neurônios de cada camada são completamente independentes de outros neurônios no mesmo nível. A última camada totalmente conectada é chamada de "camada de saída" e, nos problemas de classificação, é a distribuição de notas por classe.

As redes neurais convencionais não são bem dimensionadas para imagens maiores . No conjunto de dados CIFAR-10, as imagens têm tamanho 32x32x3 (32 pixels de altura, 32 pixels de largura, 3 canais de cores). Para processar essa imagem, um neurônio totalmente conectado na primeira camada oculta de uma rede neural normal terá 32x32x3 = 3072 pesos. Essa quantidade ainda é aceitável, mas torna-se aparente que essa estrutura não funcionará com imagens maiores. Por exemplo, uma imagem maior - 200x200x3 fará com que o número de pesos se torne 200x200x3 = 120.000. Além disso, precisaremos de mais de um desses neurônios, para que o número total de pesos comece a crescer rapidamente. Torna-se óbvio que a conectividade é excessiva e um grande número de parâmetros levará rapidamente a rede a reciclagem.

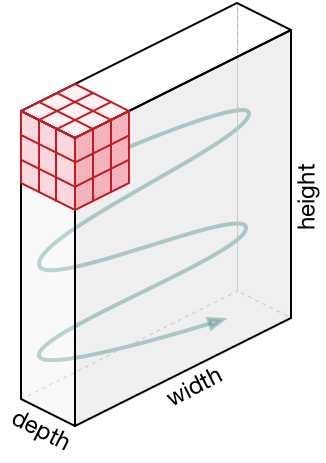
Representações em 3D de neurônios . As redes neurais convolucionais usam o fato de que os dados de entrada são imagens e, portanto, formam uma arquitetura mais sensível para esse tipo de dado. Em particular, diferentemente das redes neurais comuns, as camadas da rede neural convolucional organizam os neurônios em 3 dimensões - largura, altura, profundidade ( Nota : a palavra "profundidade" refere-se à 3ª dimensão dos neurônios de ativação, e não à profundidade da própria rede neural medida em número de camadas). Por exemplo, as imagens de entrada do conjunto de dados CIFAR-10 são dados de entrada em uma representação 3D, cuja dimensão é 32x32x3 (largura, altura, profundidade). Como veremos mais adiante, os neurônios em uma camada serão associados a um pequeno número de neurônios na camada anterior, em vez de serem conectados a todos os neurônios anteriores na camada. Além disso, a camada de saída para a imagem do conjunto de dados CIFAR-10 terá uma dimensão de 1 × 1 × 10, porque ao se aproximar do final da rede neural reduziremos o tamanho da imagem a um vetor de estimativas de classe localizadas ao longo da profundidade (3ª dimensão).

Visualização:

Rede neural padrão	Rede Neural Convolucional

Lado esquerdo: rede neural padrão de 3 camadas.
No lado direito: a rede neural convolucional possui seus neurônios em 3 dimensões (largura, altura, profundidade), como mostrado em uma das camadas. Cada camada de rede neural convolucional converte uma representação 3D da entrada em uma representação 3D da saída como neurônios de ativação. Neste exemplo, a camada de entrada vermelha contém a imagem, portanto seu tamanho será igual ao tamanho da imagem e a profundidade será de 3 (três canais - vermelho, verde, azul).

A rede neural convolucional consiste em camadas. Cada camada é uma API simples: converte a representação 3D de entrada na representação 3D de saída de uma função diferenciável, que pode ou não conter parâmetros.

Camadas usadas para construir redes neurais convolucionais

Como já descrevemos acima, uma rede neural convolucional simples é um conjunto de camadas, em que cada camada converte uma representação em outra usando uma função diferenciável. Utilizamos três tipos principais de camadas para construir redes neurais convolucionais: uma camada convolucional , uma camada de subamostragem e uma camada totalmente conectada (o mesmo que usamos em uma rede neural normal). Organizamos essas camadas seqüencialmente para obter a arquitetura SNA.

Exemplo de arquitetura: visão geral. A seguir, nos aprofundaremos nos detalhes, mas, por enquanto, para o conjunto de dados CIFAR-10, a arquitetura de nossa rede neural convolucional pode ser [INPUT -> CONV -> RELU -> POOL -> FC] . Agora com mais detalhes:

• INPUT [32x32x3] conterá os valores originais dos pixels da imagem; no nosso caso, a imagem tem 32px de largura, 32px de altura e 3 canais de cor R, G, B.
• CONV camada CONV produzirá um conjunto de neurônios de saída que serão associados à área local da imagem da fonte de entrada; cada um desses neurônios calculará o produto escalar entre seus pesos e a pequena parte da imagem original à qual está associado. O valor de saída pode ser uma representação 3D de 323212 , se, por exemplo, decidirmos usar 12 filtros.
• RELU camada RELU aplicará a função de ativação do elemento max(0, x) . Essa conversão não altera a dimensão dos dados - [32x32x12] .
• POOL camada POOL realizará a operação de amostragem da imagem em duas dimensões - altura e largura, o que, como resultado, nos dará uma nova representação 3D [161612] .
• FC camada FC (camada totalmente conectada) calculará as notas por classes, a dimensão resultante será [1x1x10] , onde cada um dos 10 valores corresponderá às notas de uma classe específica entre as 10 categorias de imagens do CIFAR-10. Como nas redes neurais convencionais, cada neurônio dessa camada será associado a todos os neurônios da camada anterior (representação 3D).

É assim que a rede neural convolucional transforma a imagem original, camada por camada, do valor inicial do pixel à estimativa final da classe. Observe que algumas camadas contêm opções e outras não. Em particular, as camadas CONV/FC realizam uma transformação, que não é apenas uma função que depende dos dados de entrada, mas também depende dos valores internos de pesos e deslocamentos nos próprios neurônios. RELU/POOL camadas RELU/POOL , RELU/POOL outro lado, usam funções não parametrizadas. Os parâmetros nas camadas CONV/FC serão treinados por descida gradiente para que a entrada receba os rótulos de saída corretos correspondentes.

Para resumir:

• A arquitetura da rede neural convolucional, em sua representação mais simples, é um conjunto ordenado de camadas que transforma a representação de uma imagem em outra representação, por exemplo, estimativas de associação de classe.
• Existem vários tipos diferentes de camadas (CONV - camada convolucional, FC - totalmente conectado, função de ativação RELU - função, POOL - camada de subamostra - a mais popular).
• Cada camada de entrada recebe uma representação 3D e a converte em uma representação 3D de saída usando uma função diferenciável.
• Cada camada pode e pode não ter parâmetros (CONV / FC - possui parâmetros, RELU / POOL - no).
• Cada camada pode e pode não ter hiper parâmetros (CONV / FC / POOL - have, RELU - no)

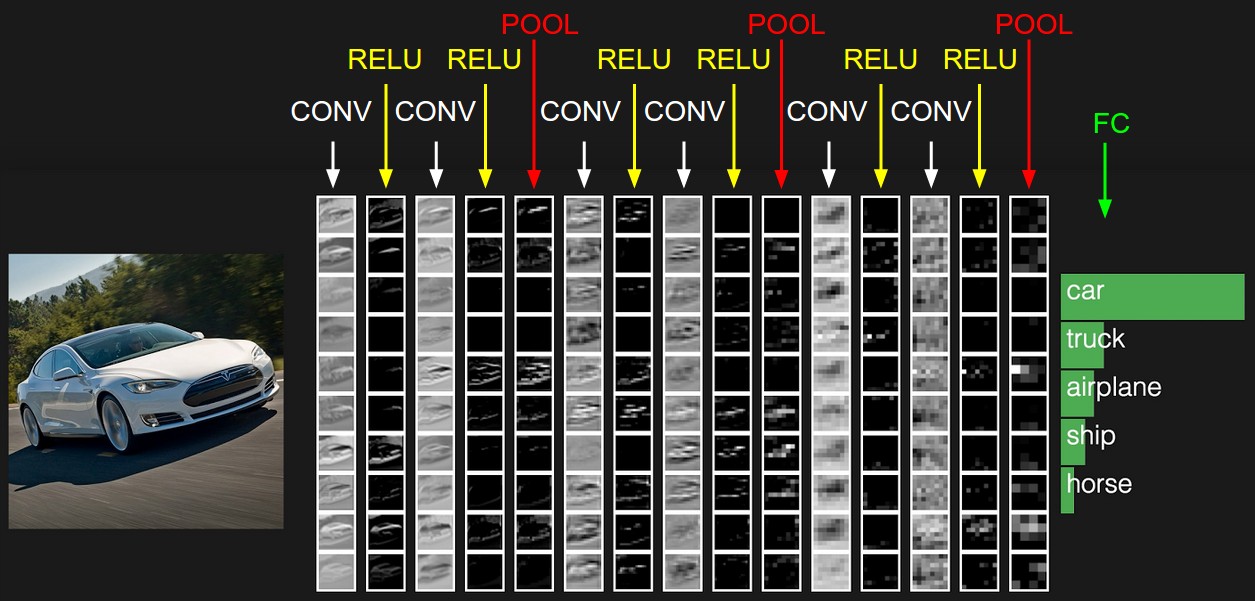
A representação inicial contém os valores de pixel da imagem (à esquerda) e estimativas para as classes às quais o objeto na imagem pertence (à direita). Cada transformação de visualização é marcada como uma coluna.

Camada convolucional

A camada convolucional é a camada principal na construção de redes neurais convolucionais.

Visão geral sem mergulhar nas características do cérebro. Vamos primeiro tentar descobrir o que a camada CONV ainda está calculando sem imergir e tocar no assunto do cérebro e dos neurônios. Os parâmetros da camada convolucional consistem em um conjunto de filtros treinados. Cada filtro é uma pequena grade ao longo da largura e altura, mas se estende por toda a profundidade da representação de entrada.

Por exemplo, um filtro padrão na primeira camada de uma rede neural convolucional pode ter dimensões 5x5x3 (5px - largura e altura, 3 - o número de canais de cores). Durante uma passagem direta, movemos (para ser exato - reduzimos) o filtro ao longo da largura e altura da representação de entrada e calculamos o produto escalar entre os valores do filtro e os valores correspondentes da representação de entrada a qualquer momento. No processo de mover o filtro ao longo da largura e altura da representação de entrada, formamos um mapa de ativação bidimensional que contém os valores da aplicação desse filtro a cada uma das áreas da representação de entrada. Intuitivamente, fica claro que a rede ensinará os filtros a serem ativados quando virem um determinado sinal visual, por exemplo, uma linha reta em um determinado ângulo ou representações em forma de roda em níveis mais altos. Agora que aplicamos todos os nossos filtros à imagem original, por exemplo, havia 12. Como resultado da aplicação de 12 filtros, recebemos 12 cartões de ativação da dimensão 2. Para produzir uma representação de saída, combinamos esses cartões (sequencialmente na 3ª dimensão) e obtemos uma representação dimensão [LxAx12].

Uma visão geral à qual conectamos o cérebro e os neurônios. Se você é um fã do cérebro e dos neurônios, pode imaginar que cada neurônio "observe" uma grande parte da representação de entrada e transfira informações sobre essa seção para os neurônios vizinhos. A seguir, discutiremos os detalhes da conectividade dos neurônios, sua localização no espaço e o mecanismo de compartilhamento de parâmetros.

Conectividade local. Quando lidamos com dados de entrada com um grande número de medições, por exemplo, como no caso de imagens, então, como já vimos, não há absolutamente nenhuma necessidade de conectar neurônios com todos os neurônios na camada anterior. Em vez disso, conectaremos apenas neurônios a áreas locais da representação de entrada. O grau espacial de conectividade é um dos hiperparâmetros e é chamado de campo receptivo (o campo receptivo de um neurônio é do tamanho do mesmo núcleo de filtro / convolução). O grau de conectividade ao longo da 3ª dimensão (profundidade) é sempre igual à profundidade da representação original. É muito importante focar nisso novamente, atenção à forma como definimos as dimensões espaciais (largura e altura) e profundidade: as conexões dos neurônios são locais em largura e altura, mas sempre se estendem por toda a profundidade da representação de entrada.

Exemplo 1. Imagine que a representação de entrada tenha um tamanho de 32x32x3 (RGB, CIFAR-10). Se o tamanho do filtro (o campo receptivo do neurônio) for 5 × 5, cada neurônio na camada convolucional terá pesos na região 5 × 5 × 3 da representação original, o que levará ao estabelecimento de 5 × 5 × 3 = 75 ligações (pesos) + 1 parâmetro de deslocamento. Observe que o grau de conexão em profundidade deve ser igual a 3, pois essa é a dimensão da representação original.

Exemplo 2. Imagine que a representação de entrada tenha um tamanho de 16x16x20. Usando como exemplo o campo receptivo de um neurônio do tamanho 3x3, cada neurônio da camada convolucional terá 3x3x320 = 180 conexões (pesos) + 1 parâmetro de deslocamento. Observe que a conectividade é local em largura e altura, mas em profundidade (20).

# 1	# 2

Do lado esquerdo: a representação de entrada é exibida em vermelho (por exemplo, uma imagem do tamanho CIFAR-10 de 32x332) e um exemplo da representação de neurônios na primeira camada convolucional. Cada neurônio na camada convolucional está associado apenas à área local da representação de entrada, mas completamente em profundidade (no exemplo, ao longo de todos os canais de cores). Observe que há muitos neurônios na imagem (no exemplo - 5) e eles estão localizados ao longo da 3ª dimensão (profundidade) - explicações sobre esse arranjo serão fornecidas abaixo.
No lado direito: os neurônios da rede neural ainda permanecem inalterados: eles ainda calculam o produto escalar entre seus pesos e dados de entrada, aplicam a função de ativação, mas sua conectividade é agora limitada pela área espacial local.

A localização espacial. Já descobrimos a conectividade de cada neurônio na camada convolucional com a representação de entrada, mas ainda não discutimos quantos desses neurônios ou como eles estão localizados. Três hiper parâmetros afetam o tamanho da visualização de saída: profundidade , passo e alinhamento .

1. A profundidade da representação de saída é um hiper parâmetro: corresponde ao número de filtros que queremos aplicar, cada um dos quais aprende algo mais na representação original. Por exemplo, se a primeira camada convolucional recebe uma imagem como entrada, então diferentes neurônios ao longo da 3ª dimensão (profundidade) podem ser ativados na presença de diferentes orientações de linhas em uma determinada área ou aglomerados de uma determinada cor. O conjunto de neurônios que "olham" para a mesma área da representação de entrada, chamaremos de coluna profunda (ou "fibra" - fibra).
2. Precisamos determinar o passo (tamanho do deslocamento em pixels) com o qual o filtro se moverá. Se a etapa for 1, mudaremos o filtro em 1 pixel em uma iteração. Se a etapa for 2 (ou, ainda menos usada, 3 ou mais), o deslocamento ocorrerá para cada dois pixels em uma iteração. Uma etapa maior resulta em uma representação de saída menor.
3. Como veremos em breve, às vezes será necessário suplementar a representação de entrada ao longo das bordas com zeros. O tamanho do alinhamento (o número de zero colunas / linhas preenchidas) também é um hiper parâmetro. Uma boa característica do uso do alinhamento é o fato de o alinhamento nos permitir controlar a dimensão da representação de saída (na maioria das vezes manteremos as dimensões originais da vista - preservando a largura e a altura da representação de entrada com a largura e a altura da representação de saída).

Podemos calcular a dimensão final da representação de saída, apresentando-a em função do tamanho da representação de entrada ( W ), do tamanho do campo receptivo dos neurônios da camada convolucional ( F ), do passo ( S ) e do tamanho do alinhamento ( P ) nas bordas. Você pode ver por si mesmo que a fórmula correta para calcular o número de neurônios na representação de saída é a seguinte (W - F + 2P) / S + 1 . Por exemplo, para uma representação de entrada do tamanho 7x7 e tamanho do filtro de 3x3, etapa 1 e alinhamento 0, obtemos uma representação de saída do tamanho 5x5. Na etapa 2, obteríamos uma representação de saída de 3x3. Vejamos outro exemplo, desta vez ilustrado graficamente:

Ilustração de um arranjo espacial. Neste exemplo, apenas uma dimensão espacial (eixo x), um neurônio com campo receptivo F = 3 , tamanho da representação de entrada W = 5 e alinhamento P = 1 . No lado esquerdo : o campo receptivo do neurônio se move com um passo S = 1 , que, como resultado, fornece o tamanho da representação de saída (5 - 3 + 2) / 1 + 1 = 5. No lado direito : o neurônio usa o campo receptivo de tamanho S = 2 , que em o resultado é o tamanho da representação de saída (5 - 3 + 2) / 2 + 1 = 3. Observe que o tamanho da etapa S = 3 não pode ser usado, pois com esse tamanho da etapa o campo receptivo não captura parte da imagem. Se usarmos nossa fórmula, então (5 - 3 + 2) = 4 não é um múltiplo de 3. Os pesos dos neurônios neste exemplo são [1, 0, -1] (como mostrado na figura à direita), e o deslocamento é zero. Esses pesos são compartilhados por todos os neurônios amarelos.

Usando alinhamento . Preste atenção ao exemplo no lado esquerdo, que contém 5 elementos na saída e 5 elementos na saída. Isso funcionou porque o tamanho do campo receptivo (filtro) era 3 e usamos o alinhamento P = 1 . Se não houvesse alinhamento, o tamanho da representação de saída seria igual a 3, porque eram precisamente tantos neurônios que caberiam lá. Em geral, definir o tamanho do alinhamento P = (F - 1) / 2 com uma etapa igual a S = 1 permite obter o tamanho da representação de saída semelhante à representação de entrada. Uma abordagem semelhante usando alinhamento é frequentemente aplicada na prática, e discutiremos os motivos abaixo quando falarmos sobre a arquitetura de redes neurais convolucionais.

Limites de tamanho da etapa . Observe que os hiperparâmetros responsáveis ​​pelo arranjo espacial também estão relacionados por limitações. Por exemplo, se a representação de entrada tiver um tamanho de W = 10 , P = 0 e o tamanho do campo receptivo F = 3 , torna-se impossível usar um tamanho de etapa igual a S = 2 , pois (W - F + 2P) / S + 1 = (10 - 3 + 0) / 2 + 1 = 4,5 , que fornece um valor inteiro do número de neurônios. Assim, essa configuração de hiper parâmetros é considerada inválida e as bibliotecas para trabalhar com redes neurais convolucionais lançam uma exceção, alinham a força ou até cortam a representação de entrada. Como veremos nas próximas seções deste capítulo, a definição dos hiperparâmetros da camada convolucional ainda é uma dor de cabeça que pode ser reduzida usando certas recomendações e "regras de bom tom" ao projetar a arquitetura de redes neurais convolucionais.

Exemplo da vida real . Arquitetura de rede neural convolucional Krizhevsky et al. , que venceu o concurso ImageNet em 2012, recebeu 227x227x3 imagens. Na primeira camada convolucional, ela utilizou um campo receptivo de tamanho F = 11 , passo S = 4 e tamanho de alinhamento P = 0 . Como (227 - 11) / 4 + 1 = 55, e a camada convolucional tinha K = 96 de profundidade, a dimensão de saída da apresentação era 55x55x96. Cada um dos neurônios 55x55x96 nessa representação foi associado a uma região de tamanho 11x11x3 na representação de entrada. Além disso, todos os 96 neurônios da coluna profunda estão associados à mesma região 11x11x3, mas com pesos diferentes. E agora um pouco de humor - se você se familiarizar com o documento original (estudo), observe que o documento afirma que a entrada recebe imagens de 224x224, o que não pode ser verdade, porque (224 - 11) / 4 + 1 de forma alguma forneça um valor inteiro. Esse tipo de situação costuma ser confundido para pessoas em histórias com redes neurais convolucionais. Meu palpite é que Alex usou o tamanho de alinhamento P = 3 , mas esqueceu de mencionar isso no documento.

Opções de compartilhamento. O mecanismo para compartilhar parâmetros em camadas convolucionais é usado para controlar o número de parâmetros. Preste atenção ao exemplo acima, como você pode ver, existem 55x55x96 = 290.400 neurônios na primeira camada convolucional e cada um dos neurônios possui 11x11x3 = 363 pesos + 1 valor de deslocamento. No total, se multiplicarmos esses dois valores, obteremos 290400x364 = 105 705 600 parâmetros apenas na primeira camada da rede neural convolucional. Obviamente, isso é de grande importância!

Acontece que é possível reduzir significativamente o número de parâmetros fazendo uma suposição: se alguma propriedade calculada na posição (x, y) é importante para nós, então essa propriedade calculada na posição (x2, y2) também será importante para nós. Em outras palavras, denotando uma "camada" bidimensional em profundidade como uma "camada profunda" (por exemplo, a exibição [55x55x96] contém 96 camadas profundas, cada uma com tamanho de 55x55), construiremos neurônios em profundidade com os mesmos pesos e deslocamento. Com esse esquema de compartilhamento de parâmetros, a primeira camada convolucional em nosso exemplo agora conterá 96 conjuntos de pesos exclusivos (cada conjunto para cada camada de profundidade); no total, haverá 96x11x11x3 = 34.848 pesos exclusivos ou 34.944 parâmetros (+96 deslocamentos). Além disso, todos os neurônios 55x55 em cada camada profunda agora usarão os mesmos parâmetros. Na prática, durante a propagação traseira, cada neurônio nesta representação calculará o gradiente para seus próprios pesos, mas esses gradientes serão somados em cada camada de profundidade e atualizarão apenas um único conjunto de pesos em cada nível.

Observe que, se todos os neurônios da mesma camada profunda usassem os mesmos pesos, para propagação direta através da camada convolucional, a convolução entre os valores dos pesos dos neurônios e os dados de entrada seria calculada. É por isso que é costume chamar um único conjunto de pesos - um filtro (núcleo) .

Exemplos de filtros que foram obtidos treinando o modelo Krizhevsky et al. Cada um dos 96 filtros mostrados aqui tem tamanho 11x11x3 e cada um deles é compartilhado por todos os neurônios 55x55 de uma camada profunda. Observe que a suposição de compartilhar os mesmos pesos faz sentido: se a detecção de uma linha horizontal é importante em uma parte da imagem, é intuitivamente claro que essa detecção é importante em outra parte da imagem. Portanto, não faz sentido treinar novamente para encontrar linhas horizontais em cada um dos 55x55 locais diferentes da imagem na camada convolucional.

Deve-se ter em mente que a suposição de compartilhar parâmetros nem sempre faz sentido. Por exemplo, se uma imagem com alguma estrutura centralizada for inserida na entrada de uma rede neural convolucional, onde gostaríamos de poder aprender uma propriedade em uma parte da imagem e outra propriedade na outra parte da imagem. Um exemplo prático são as imagens de face centralizada. Pode-se assumir que diferentes sinais oculares ou capilares podem ser identificados em diferentes áreas da imagem; portanto, nesse caso, o relaxamento dos pesos é usado e a camada é chamada conectada localmente .

Exemplos numpy . As discussões anteriores devem ser transferidas para o plano de detalhes e em exemplos com código. Imagine que a representação de entrada seja uma matriz numpy de X Então:

• A coluna profunda ( linha ) na posição (x,y) será representada da seguinte forma X[x,y,:] .
• A camada profunda , ou como anteriormente chamamos de camada - o mapa de ativação na profundidade d será representado da seguinte forma X[:,:,d] .

Um exemplo de uma camada convolucional . , X X.shape: (11,11,4) . , P=1 , () F=5 S=1 . 44, — (11-5)/2+1=4. ( V ), ( ):

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

, numpy , * . , W0 b0 . W0 W0.shape: (5,5,4) , 5, 4. . , , 2 ( ). :

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1 (, y )
• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1 (, )

— W1 b1 . , V . , , , ReLU , . .

. :

• W1 x H1 x D1
• 4 -:
  
  • K ,
  • F ,
  • S ,
  • P .
• W2 x H2 x D2 ,
  
  • W2 = (W1 — F + 2P)/S + 1
  • H2 = (H1 — F + 2P)/S + 1
  • D2 = K
• F x F x D1 , (F x F x D1) x K K .
• , d - ( W2 x H2 ) d - S d -.

- F = 3, S = 1, P = 1 . . " ".

. . 3D- ( — , — , — ), — . W1 = 5, H1 = 5, D1 = 3 , K = 2, F = 3, S = 2, P = 1 . , 33, 2. (5 — 3 + 2)/2 + 1 = 3. , , P = 1 . , () , .

( , html+css , )

. (). :

1. im2col . , 227x227x3 11113 4, 11113 = 363 . , 4 , (227 — 11) / 4 + 1 = 55 , X_col 3633025, 3025. , , , (), .
2. . , 96 11113, W_row 96363.
3. — np.dot(W_row, X_col) , . 963025.
4. 555596.

, , — , . , , — (, BLAS API). , im2col , .

. ( ) ( , ) ( - ). , .

11 . 11, Network in Network . , 11, , . , 2- , 11 ( ). , , 3- , . , 32323, 11, , , 3 (R, G, B — , ).

. - . . , . w 3 x : w[0] x[0] + w[1] x[1] + w[2] x[2] . 0. 1 : w[0] x[0] + w[1] x[2] + w[2] x[4] . "" 1 . , . , 2 33, , 55 ( 55 ). .

— . , , . , MAX. 22 2, 2 , 75% . MAX 22. . , :

• W1 x H1 x D1
• 2 -:
  
  • F ,
  • S ,
• W2 x H2 x D2 , :
  
  • W2 = (W1 — F)/S + 1
  • H2 = (H1 — F)/S + 1
  • D2 = D1
• ,
• (zero-padding ).

, : F=3, S=2 ( ), — F=2, S=2 . - .

. , , , L2-. , , .

#1	#2

. : 22422464 22 2, 11211264. , . : — (max-pooling), 2. 4 ( 22)

. , max(a,b) — . , ( ), .

. , . , : , . . , (VAEs) (GANs). , - , .

, , . , , . .

, . .

, , ( ). - , . , :

• , . , , , , , .
• , . , K=4096 ( ), 7712 - F=7, P=0, S=1, K=4096 . , 114096, .

. , . , 2242243 77512 ( AlexNet, , 5 , 7 — 224/2/2/2/2/2 = 7). AlexNet 4096 , , 1000 , . :

• , "" 77512, F=7 , 114096.
• F=1 , 114096.
• F=1 , 111000.

, , ( ) W . , "" () .

, 224224 , 77512 — 32 , 384384 1212512, 384/32 = 12. , , , 661000, (12 — 7)/1 + 1 = 6. , 111000 66 384384 .

( ) 384384, 224244 32 , , .

, , 36 , 36 . , , . .

, , 32 ? ( ). , 16 , 2 : 16 .

, , 3 : , ( , ) . ReLU , - . .

CONV-RELU-, POOL- , . - . , , . , :

 INPUT -> [[CONV -> RELU]*N -> POOL?] * M -> [FC -> RELU]*K -> FC 

* , POOL? . , N >= 0 ( N <= 3 ), M >= 0 , K >= 0 ( K < 3 ). , , :

• INPUT -> FC , . N = M = K = 0 .
• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL] * 2 -> FC -> RELU -> FC , .
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL] * 3 -> [FC -> RELU] * 2 -> FC . 2 . , , .

. 3 33 ( RELU , ). "" 33 . "" 33 , — 55. "" 33 , — 77. , 33 77. "" 77 ( ) , . -, , 3 , . -, C , , 77 (C(77)) = 49xxC , 33 3((33)) = 27 . , , . — , .

. , , Google, Microsoft. .

: , ImageNet. , , 90% . — " ": , , , ImageNet — , . .

-, . , :

( ) 2 . 32 (, CIFAR-10), 64, 96 (, STL-10), 224 (, ImageNet), 384 512.

(, 33 , 55), S=1 , , , . , F=3 P=1 . F=5, P=2 . F , P=(F-1)/2 . - ( 77), .

. 22 ( F=2 ) 2 ( S=2 ). , 75% (- , ). , , 33 ( ) 2 ( ). 33 , . .

. , , . , 1 , , .

1 ? . , 1 ( ), .

? , . , , , .

. ( ), , . , 64 33 1 2242243, 22422464. , , 10 , 72 ( , ). GPU, . , 77 2. , AlexNet, 1111 4.

. :

• LeNet . Yann LeCun 1990. LeNet , ZIP-, .
• AlexNet . , , Alex Krizhevsky, Ilya Sutskever Geoff Hinton. AlexNet ImageNet ILSVRC 2012 ( : 16% 26%). LeNet, , ( ).
• ZFNet . ILSVRC 2013 Matthew Zeiler Rob Fergus. ZFNet. AlexNet, -, .
• GoogLeNet . ILSVRC 2014 Szegedy et al. Google. Inception-, (4 60 AlexNet). , , . , — Inveption-v4.
• VGGNet . 2014 ILSVRC Karen Simonyan Andrew Zisserman, VGGNet. , . 16 + (33 22 ). . VGGNet — (140). , , , .
• ResNet . Residual- Kaiming He et al. ILSVRC 2015. . . ( 2016).

VGGNet . VGGNet . VGGNet , 33, 1 1, 22 2. ( ) :

 INPUT: [224x224x3] memory: 224*224*3=150K weights: 0 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*3)*64 = 1,728 CONV3-64: [224x224x64] memory: 224*224*64=3.2M weights: (3*3*64)*64 = 36,864 POOL2: [112x112x64] memory: 112*112*64=800K weights: 0 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*64)*128 = 73,728 CONV3-128: [112x112x128] memory: 112*112*128=1.6M weights: (3*3*128)*128 = 147,456 POOL2: [56x56x128] memory: 56*56*128=400K weights: 0 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*128)*256 = 294,912 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 CONV3-256: [56x56x256] memory: 56*56*256=800K weights: (3*3*256)*256 = 589,824 POOL2: [28x28x256] memory: 28*28*256=200K weights: 0 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*256)*512 = 1,179,648 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [28x28x512] memory: 28*28*512=400K weights: (3*3*512)*512 = 2,359,296 POOL2: [14x14x512] memory: 14*14*512=100K weights: 0 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 CONV3-512: [14x14x512] memory: 14*14*512=100K weights: (3*3*512)*512 = 2,359,296 POOL2: [7x7x512] memory: 7*7*512=25K weights: 0 FC: [1x1x4096] memory: 4096 weights: 7*7*512*4096 = 102,760,448 FC: [1x1x4096] memory: 4096 weights: 4096*4096 = 16,777,216 FC: [1x1x1000] memory: 1000 weights: 4096*1000 = 4,096,000 TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd) TOTAL params: 138M parameters 

, , ( ) , . 100 140 .

. GPU 3/4/6 , GPU — 12 . , :

• : , ( ). , . , .
• : , , . , , 3 .
• , , ..

(, ), . , 4 ( 4 , — 8), 1024 , , . " ", , .

… call-to-action — , share :)
YouTube
Telegram
VKontakte