👩🏿‍🎤 🧑🏽‍🤝‍🧑🏻 🛎️ O mundo da hiperesfera tridimensional. Rastreamento de raios geodésicos em um universo fechado com geometria esférica 👩🏿‍💼 ↘️ ⛱️

Você gostaria de ver o mundo através dos olhos de uma criatura vivendo em um universo compacto e fechado com geometria esférica? Ver o mundo sem uma noite? Um mundo onde o outro pólo do planeta é visível no céu? Um mundo onde não há diferença entre um eclipse solar e um eclipse lunar? Bem-vindo ao gato!

1. Introdução Mundo fechado bidimensional

Para entender melhor o que acontecerá a seguir, imagine que você é um ser bidimensional e vive em um mundo bidimensional que representa uma esfera. Como você perceberá seu mundo? Vamos começar determinando a posição dos corpos. Você pode declarar o ponto em que você é o "centro do universo", selecionar dois vetores de unidades mutuamente perpendiculares e usar o sistema de coordenadas cartesiano resultante nas proximidades do "centro do universo".

No entanto, à medida que você se afasta do "centro do universo", coisas estranhas começarão a acontecer. O que você percebeu como linhas perpendiculares, a uma certa distância do "centro do universo", se transforma no que você percebe como linhas paralelas ...

... E linhas paralelas se cruzam.

A razão é simples - o que você percebe como uma linha reta é realmente um grande círculo - a linha geodésica da esfera. Portanto, o sistema de coordenadas cartesianas é inadequado para determinar a posição dos corpos em seu mundo - quando você se afasta do "centro do universo", ele perde seu significado.

Você terá que escolher outro, mais adequado para uso em seu mundo, sistema de coordenadas - polar . Este sistema de coordenadas é natural e consistente. De fato - o ângulo entre o eixo polar e a direção do corpo permanece constante, independentemente da distância do corpo.

Sendo capaz de determinar a posição dos corpos, podemos explorar mentalmente seu mundo e descrever alguns efeitos que aparecem quando você se afasta do "centro do universo" e devido ao fato de seu mundo ser uma esfera.

A perspectiva inversa . Geralmente, quando um corpo se afasta do "centro do universo", seu tamanho angular diminui. No entanto, a uma distância de mais de um quarto do comprimento da linha geodésica do "centro do universo" com a remoção do corpo, seu tamanho angular aumentará. Esse efeito se deve ao fato de que a distância entre as linhas geodésicas da esfera e o equador aumenta e depois que o equador diminui. Um corpo remoto à mesma distância do equador terá o mesmo tamanho angular, independentemente de qual lado esteja do equador. E esse tamanho angular será maior que o tamanho angular do corpo no equador.

Esticando o corpo em todo o céu. Aqui, o termo céu inteiro é usado em significado - todo o campo de visão de um ser bidimensional (superior e inferior ou dianteiro e traseiro). Se o corpo estiver próximo do ponto oposto ao "centro do universo", então, onde quer que você olhe, encontrará seu olhar com esse corpo. O corpo não terá um ponto que não pode ser visto - cada ponto tem um lugar no céu. Este é o caso final do efeito de perspectiva inversa.

Transformação simétrica tel. Se o corpo estiver a uma distância superior a metade do comprimento da linha geodésica do "centro do universo", você verá esse corpo transformado simetricamente - os lados esquerdo e direito do corpo mudarão de lugar. Normalmente, os raios esquerdo e direito emitidos do "centro do universo" caem nos lados esquerdo e direito do corpo. No entanto, a uma distância de metade do comprimento da linha geodésica do "centro do universo", os raios se cruzam e, após o cruzamento, caem nos lados opostos do corpo.

As segundas perspectivas para frente e para trás. Esse efeito também é observado se o corpo estiver a uma distância maior que a metade do comprimento da linha geodésica do "centro do universo". A distâncias de metade a três quartos do comprimento da linha geodésica do “centro do universo”, com a remoção do corpo, seu tamanho angular diminuirá novamente (perspectiva direta). A distâncias de três quartos a todo o comprimento da linha geodésica do “centro do universo”, à medida que o corpo se afasta, seu tamanho angular aumentará novamente (perspectiva reversa). Esse efeito, bem como o efeito de perspectiva inversa, está associado a uma mudança na distância entre as linhas geodésicas da esfera - no caminho de volta ao "centro do universo", a distância entre as linhas geodésicas da esfera e o equador aumenta e diminui após o equador.

Duplas. Cada corpo em seu mundo terá um dobro - se você vir um corpo à sua frente, girando ao redor poderá ver seu lado oposto (duplo). Um raio emitido ao longo de um longo caminho percorre o seu mundo e entra na parte de trás do corpo. Deve-se notar que a superfície do duplo será aquela parte da superfície que você não vê à sua frente e será simetricamente transformada. Aqui, o termo superfície é usado no significado - a fronteira de um corpo bidimensional percebido por um ser bidimensional - aplicado a um círculo; na verdade, é um arco circular percebido por um ser bidimensional como um segmento; no entanto, para maior clareza, destacaremos não apenas o arco, mas também a parte do círculo atrás dele.

A passagem do corpo através de um ponto oposto ao "centro do universo". Como o efeito de esticar o corpo para todo o céu é muito incomum, consideraremos mais detalhadamente. Nas figuras: a vizinhança de um ponto oposto ao "centro do universo".

Vê-se que:

primeiro, a superfície do corpo à sua frente aumenta (pintada de azul) e a superfície atrás de você diminui (pintada de azul); ao mesmo tempo, ambas as superfícies têm as mesmas dimensões angulares - ou seja, a superfície do corpo localizada à sua frente é contraída (a parte maior da superfície fica em cada grau) e a que fica atrás de você é esticada (a parte menor da superfície fica em cada grau)
quando o corpo toca um ponto oposto ao "centro do universo", o tamanho angular de ambas as superfícies é de 180 graus - metade do céu (à sua frente) ocupa toda a superfície do corpo e a segunda metade do céu (atrás de você) é ocupada por um ponto na parte de trás do corpo
enquanto o centro do corpo está alinhado com o ponto oposto ao "centro do universo", o processo de puxar e esticar inversamente
quando o corpo está localizado em um ponto oposto ao "centro do universo", sua superfície fica sem distorção estendida por todo o céu
corpo deslizando de um ponto oposto ao "centro do universo" parece semelhante

Horizonte duplo. Imagine que você mora em um planeta bidimensional. Olhando para baixo, você vê a superfície do seu lado do planeta, e olhando para cima, você vê ... a superfície da parte de trás do planeta. Além disso, será muito apertado - você pode ver a superfície da parte traseira do planeta e a parte da superfície do seu lado do planeta que está atrás das costas atrás do horizonte - você pode ver tudo isso acima da sua cabeça. O céu será apresentado na forma de uma faixa estreita como um fio, ensanduichada de cima e de baixo pelos horizontes de vocês e dos lados opostos do planeta. Esta é uma combinação do efeito de esticar o corpo por todo o céu e o efeito de um duplo. Em geral, no seu mundo, se nada atrapalhar seu olhar, logo à sua frente você poderá ver sua nuca ... uma nuca saudável, em todos os detalhes ... estendida a todo o céu)

Um mundo sem noite. Imagine que o planeta bidimensional em que você vive gira em torno de uma estrela bidimensional. A luz emitida por uma estrela em um caminho curto cai no lado diurno do planeta. Ao mesmo tempo, a luz emitida por uma estrela ao longo de um longo caminho percorre seu mundo e cai no lado noturno do planeta. A noite não existe mais. Tudo o que resta são pôr-do-sol e nascer do sol, o que ocorrerá simultaneamente - quando o lado da estrela que está de frente para você começa a ir além do horizonte, o lado de trás da estrela começa a se erguer atrás de você por trás do horizonte. Obviamente, você pode destacar o verdadeiro pôr do sol e o amanhecer ao longo do caminho que a luz passou, mas será quase impossível diferenciá-los dos duplos.

Há também um caso extremo. Se o planeta tiver azar e estiver no ponto da estrela oposta, a estrela será esticada para todo o céu, mas será problemático admirá-la, pois toda a luz emitida pela estrela cairá no planeta (na ausência de absorção e dispersão da luz pelo meio interplanetário).

Eclipses solares e lunares. Imagine que um satélite natural bidimensional gira em torno de um planeta bidimensional no qual você vive. Quando um satélite se torna entre um planeta e uma estrela, sua sombra cai no planeta. Por outro lado, ao mesmo tempo, o planeta fica entre a luz emitida pela estrela ao longo de um longo caminho e o satélite, ou seja, a sombra do planeta cai no satélite. Um eclipse solar e lunar simultâneo ocorre. Obviamente, é possível distinguir os verdadeiros eclipses solares e lunares ao longo do caminho que a luz passou, mas será praticamente impossível distingui-los dos gêmeos. Cair na sombra que cai no planeta e seu satélite durante eclipses é a única maneira de ficar no escuro em seu mundo)

Mundo fechado tridimensional

Acima, examinamos o maravilhoso mundo de um ser bidimensional. E quanto a nós seres tridimensionais? Qual é a geometria do universo ? Infelizmente, a ciência ainda não pode responder a essa pergunta. Principalmente as propriedades e o tamanho do universo interferem. Vamos tentar ajudar a ciência. Selecionamos como candidato o universo fechado mais interessante com geometria esférica e o examinamos visualmente. Haverá efeitos descobertos por nós para um análogo bidimensional? Talvez nós vamos aprender algo novo? Algo que você não esperava saber? Ou até mesmo ver o que vemos todos os dias, mas não preste atenção nisso? Como será esse universo?

Modelo

Vamos explorar o mundo, que é uma hiperesfera tridimensional (3 esferas) - ou seja, uma esfera situada no espaço quadridimensional. Escolhemos um tipo de objeto para visualização - uma esfera (uma esfera 2 pertencente a uma esfera 3).

Conceitos e relacionamentos básicos

Coordenadas cartesianas no espaço quadridimensional - as designaremos como

$(x_0, x_1, x_2, x_3)$ - isso é realmente

$(x, y, z, w)$ .

Coordenadas hiperesféricas no espaço quadridimensional (usamos apenas ângulos, uma vez que o raio do nosso mundo será uma constante) - iremos denotá-las como

$(a_0, a_1, a_2)$ - isso é realmente

$(\ phi, \ theta, \ psi)$ .

Esfera 3 centrada na origem - um conjunto de pontos cujo vetor raio possui um comprimento igual ao raio da esfera 3

$R$ É o nosso mundo

$\ quad \ quad x_0 ^ 2 + x_1 ^ 2 + x_2 ^ 2 + x_3 ^ 2 = R ^ 2$

Esfera 2 pertencente à esfera 3 - um conjunto de pontos cujo vetor raio possui um comprimento igual ao raio da esfera 3

$R$ e formas com o vetor raio do centro da esfera 2

$c$ ângulo igual ao raio angular da 2-esfera

$r_a$ Nossos objetos de visualização

$\ quad \ quad x_0 c_0 + x_1 c_1 + x_2 c_2 + x_3 c_3 = R ^ 2 \ cos r_a$

onde

$\ quad \ quad r_a = r / R$

$\ quad \ quad r$ - raio geodésico de uma esfera 2

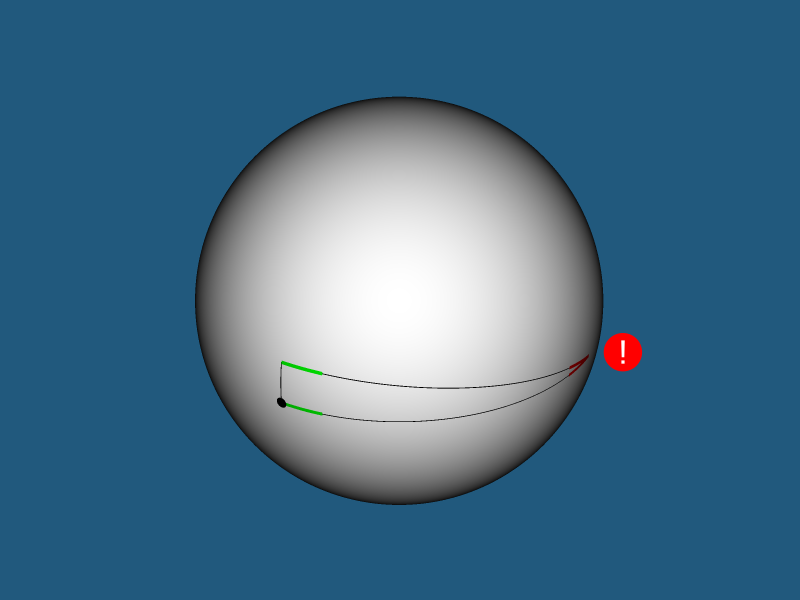
Raio geodésico, angular e condicional - para entender melhor o que é, considere um análogo bidimensional de uma esfera 2 pertencente a uma esfera 3 - um círculo pertencente a uma esfera.

O arco vermelho na figura é o raio geodésico do círculo

$r$ . O canto vermelho no lado direito da figura é o raio angular do círculo

$r_a = r / R$ . A altura do triângulo no lado direito da figura é o raio condicional do círculo

$r_n = R \ sin r_a$ .

Transição de coordenadas hiperesféricas

$(a_0, a_1, a_2)$ para cartesiano

$(x_0, x_1, x_2, x_3)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

onde

$\ quad \ quad a_0$ varia de

$0$ antes

$2 \ pi$

$\ quad \ quad a_1$ varia de

$0$ antes

$\ pi$

$\ quad \ quad a_2$ varia de

$0$ antes

$\ pi$

A interseção da linha geodésica de uma 3 esfera com uma 2 esfera pertencente a uma 3 esfera.
Essa proporção será usada para o traçado de raios. Haja uma linha geodésica que se estende do polo da 3-esfera

$(0, 0, 0, R)$ na direção definida por ângulos

$a_0$ e

$a_1$ - esses ângulos coincidem com os ângulos que determinam a direção no espaço tridimensional nas proximidades do polo tridimensional

$(0, 0, 0, R)$

$\ quad \ quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ quad \ quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ quad \ quad x_2 = R \ sin a_2 \ cos a_1$

$\ quad \ quad x_3 = R \ cos a_2$

simplificando temos (1)

$\ quad \ quad x_0 = r_0 \ sin a_2$

$\ quad \ quad x_1 = r_1 \ sin a_2$

$\ quad \ quad x_2 = r_2 \ sin a_2$

$\ quad \ quad x_3 = r_3 \ cos a_2$

onde

$\ quad \ quad r_0 = R \ sin a_1 \ cos a_0$

$\ quad \ quad r_1 = R \ sin a_1 \ sin a_0$

$\ quad \ quad r_2 = R \ cos a_1$

$\ quad \ quad r_3 = R$

substituindo (1) na equação da 2-esfera e simplificando, temos (2)

$\ quad \ quad A \ sin a_2 + B \ cos a_2 = C$

onde

$\ quad \ quad A = r_0 c_0 + r_1 c_1 + r_2 c_2$

$\ quad \ quad B = r_3 c_3$

$\ quad \ quad C = R ^ 2 \ cos r_a$

substituindo (1) na equação da 3-esfera e simplificando, temos (3)

$\ quad \ quad D \ sin ^ 2 a_2 + E \ cos ^ 2 a_2 = F$

onde

$\ quad \ quad D = r_0 ^ 2 + r_1 ^ 2 + r_2 ^ 2$

$\ quad \ quad E = r_3 ^ 2$

$\ quad \ quad F = R ^ 2$

expressando de (2)

$\ cos a_2$ nós temos

$\ quad \ quad \ cos a_2 = (C - A \ sen a_2) / B$

substituindo em (3)

$\ cos a_2$ nós temos

$\ quad \ quad D \ sin ^ 2 a_2 + E / B ^ 2 (C - A \ sin a_2) ^ 2 = F$

simplificando, temos

$\ quad \ quad a \ sin ^ 2 a_2 + b \ sin a_2 + c = 0$

onde

$\ quad \ quad m = E / B ^ 2$

$\ quad \ quad a = m A ^ 2 + D$

$\ quad \ quad b = -2 m A C$

$\ quad \ quad c = m C ^ 2 - F$

Um ponto na continuação da linha geodésica de uma 3-esfera passando por dois pontos.
Essa relação será usada para encontrar as coordenadas da textura e o normal externo em um ponto arbitrário da 2-esfera pertencente à 3-esfera. Vamos

$\ quad \ quad O$ - centro de 3 esferas

$\ quad \ quad A$ - centro da 2-esfera

$\ quad \ quad B$ É um ponto arbitrário da 2-esfera

$\ quad \ quad C$ - o ponto desejado na continuação da linha geodésica

$AB$ a uma pequena distância angular

$\ delta$ do ponto

$B$

$\ quad \ quad D$ - ponto de interseção das linhas

$AB$ e

$OC$

$\ quad \ quad E$ - o ponto de intersecção da linha que passa pelo ponto

$D$ perpendicular a reta

$AB$ e uma linha passando por um ponto

$O$ paralelo a reto

$AB$

$\ quad \ quad r_a$ - raio angular de uma esfera 2

$\ quad \ quad a = (\ pi - r_a) / 2$

$\ quad \ quad b = a - \ delta$
Se

$r_a> \ pi$ então deve ser colocado

$r_a = 2 \ pi - r_a$ e

$\ delta = - \ delta$
Vai encontrar

$\ vec {OD}$

$\ quad \ quad \ vec {OD} = \ vec {OA} + \ vec {AB} / | \ vec {AB} | \ cdot | \ vec {AD} |$

onde

$\ quad \ quad | \ vec {AD} | = | \ vec {AB} | / 2 + | \ vec {OE} |$

$\ quad \ quad | \ vec {OE} | = | \ vec {DE} | / \ tan b$

$\ quad \ quad | \ vec {DE} | = R \ sin a$

vai encontrar

$\ vec {OC}$

$\ quad \ quad \ vec {OC} = \ vec {OD} / | \ vec {OD} | \ cdot R$

Iluminação

Vamos usar dois modelos de iluminação.

Modelo de iluminação simples. Nesse modelo, o brilho de um ponto de superfície depende do cosseno do ângulo entre o normal externo à superfície e a direção do observador. Vamos usá-lo na construção de imagens para material explicativo. De fato, este é um modelo com uma fonte de luz pontual localizada onde o observador está localizado, no qual o brilho de um ponto de superfície não depende da distância da fonte de luz.

Modelo de iluminação realista. Este modelo terá uma fonte pontual de luz dedicada. Vamos usá-lo na criação de imagens realistas. Este modelo pode levar em consideração a influência da área da frente de onda no brilho de um ponto de superfície (de fato, a influência da distância da fonte de luz). Em um universo fechado com geometria esférica, a área da frente de onda é diretamente proporcional ao quadrado do raio condicional da esfera com um raio geodésico igual à distância do ponto de superfície à fonte de luz. Com a distância da fonte de luz, a área da frente de onda em relação ao equador aumenta (os raios de luz divergem) e depois que o equador diminui (os raios de luz convergem, o foco). Depois de passar o ponto oposto ao "centro do universo", ocorre o processo inverso: os raios de luz primeiro divergem e depois convergem novamente. Além disso, esse modelo pode levar em consideração as peculiaridades da percepção ( lei de Weber - Fechner ).

Para construir a imagem, usaremos o traçado de raios reversos . Para que o modelo seja interativo (examinaremos nosso mundo e nos moveremos nele), a imagem deve ser construída em tempo real. Portanto, executaremos os cálculos no shader de fragmento (usamos o WebGL). Implementamos a interface em JavaScript.

Texturas

Texture earth.jpg daqui

Textura moon.jpg daqui

Texture sun.png daqui

Primeiro conhecido

Criaremos um mundo fechado tridimensional com um comprimento de linha geodésica de 100 - para que seja mais fácil navegar - o equador do nosso mundo estará localizado a uma distância de 25 (um quarto do comprimento da linha geodésica) e o pólo oposto do nosso mundo - a uma distância de 50 (metade do comprimento da linha geodésica). Colocamos um planeta em nosso mundo e pintamos partes de sua superfície em cores, dependendo de qual octante elas se enquadram:

Octante	Sinal X	Sinal Y	Sinal z	Cor
Eu	+	+	+	Vermelho (vermelho)
II	-	+	+	Verde ( G reen)
III	-	-	+	Azul ( B lue)
IV	+	-	+	Laranja
V	+	+	-	Azul (Cian)
VI	-	+	-	Roxo ( M agenta)
VII	-	-	-	Amarelo (amarelo)
VIII	+	-	-	Branco

Como textura principal, usaremos a textura de um tabuleiro de xadrez 3x6, ou seja, cada paralelo e meridiano passarão exatamente por 12 células. Como textura alternativa, usaremos a textura do globo. Abaixo estão fotos de um sobrevôo de familiarização do nosso planeta.

Um instantâneo do Polo Norte. O eixo X é direcionado para a direita, o eixo Y é direcionado para cima, o eixo Z é direcionado para nós. Ao aplicar uma textura alternativa, você pode ver:

à direita é o Oceano Pacífico
Acima - América do Norte
esquerda - Oceano Atlântico
inferior - Eurásia

Imagens do voo do Polo Norte para o equador e do equador para o Polo Sul.

Instantâneo do Polo Sul. O eixo X é direcionado para a direita, o eixo Y é direcionado para baixo, o eixo Z é direcionado para longe de nós. Ao aplicar uma textura alternativa, você pode ver:

Direito - Oceano Pacífico, Nova Zelândia, Austrália
de cima - Oceano Índico
esquerda - Oceano Atlântico, África
bottom - América do Sul

Estudo visual

Conduziremos um estudo visual de nosso mundo para descobrir análogos dos efeitos que descobrimos em um mundo fechado bidimensional.

Duplas. Como no análogo bidimensional, cada corpo em nosso mundo terá um duplo - se virmos o Pólo Norte à nossa frente, virando-nos, poderemos ver ... o Pólo Sul. A contração da superfície do duplo é perceptível devido ao fato de estarmos perto o suficiente do planeta.

Um experimento no qual o observador se afasta do planeta (a figura no canto superior esquerdo de cada imagem é a distância entre o observador e o planeta).

Vê-se que:

inicialmente o tamanho angular do planeta diminui - essa é a perspectiva direta usual
então, quando o planeta passa pelo equador do nosso mundo (distância superior a 25), seu tamanho angular aumenta - esse é o efeito da perspectiva oposta que nos é familiar
ao rastejar para o polo oposto do mundo, vemos uma superfície contraída (distância 46.875)
quando o planeta está no polo oposto do nosso mundo (distância 50), ele se estende por todo o céu
ao deslizar do polo oposto do mundo, vemos uma superfície esticada (distância 53.125)
depois que o planeta passou pelo polo oposto do nosso mundo, ele parece simetricamente transformado - o octante vermelho mudou em azul e assim por diante
então, o tamanho angular do planeta diminui (distância de 50 a 75) e depois aumenta (distância de 75 a 100) - esse é o efeito familiar das segundas perspectivas para frente e para trás

Artefatos. Ao usar o modelo, percebeu-se que durante a passagem do planeta pelos pontos situados do observador nas distâncias de 25, 50 e 75, artefatos podem aparecer - a lã pode "crescer" no planeta ou até "desmoronar". Aparentemente, minha matemática não leva em conta alguma coisa)

Uma imagem do planeta nas proximidades do pólo oposto do nosso mundo (uma "lente" grande angular foi usada). A superfície do planeta à nossa frente é muito estreita - você pode ver não apenas todo o hemisfério norte, mas também uma parte do hemisfério sul atrás do equador. A superfície do planeta atrás de nós é muito esticada - o Polo Sul é visível com destaque. Ambas as superfícies se esticam uma na outra, tentando nos envolver em uma concha esférica e nos revelar uma imagem de um planeta esticado no céu.

Um experimento em que o observador olha para cima (o número no canto superior esquerdo de cada figura é o ângulo entre a direção descendente e o olhar).

Nas fotos:

aparece pela primeira vez o horizonte do nosso lado do planeta
então, vemos um segundo horizonte acima, onde encontramos o que está localizado do nosso lado do planeta, atrás das costas, atrás do horizonte
olhando para cima, vemos a parte de trás do planeta

Imagem de horizonte duplo (“lente” de grande angular usada). A faixa do céu é grande o suficiente porque estamos a uma altitude de cerca de 50 km.

Uma imagem do céu acima da cabeça (foi usada uma "lente grande angular").

Um mundo sem noite.
Além disso, por simplicidade, chamaremos nosso planeta Terra, seu satélite natural - a Lua e a estrela em torno da qual eles giram - de Sol. As proporções dos tamanhos do Sol, Terra, Lua e suas órbitas para maior clareza não serão observadas.
Na foto: a fronteira entre os lados diurno e noturno do planeta passando pelo Oceano Atlântico. Ao mesmo tempo, a Terra minguante e crescente é visível. Os caras sentados nas bases lunares do mundo vêem uma imagem aproximadamente semelhante)

Em animação: o movimento da fronteira entre os lados diurno e noturno da Terra. Você pode ver a sobreposição do Sol pelo disco da Terra iluminado pelos raios do Sol liberados ao longo de um longo caminho.

Eclipses solares e lunares.
Foto: A lua emerge da sombra da Terra. Os limites entre os lados do dia e da noite da Terra e da Lua são visíveis.

Em animação: eclipses solares e lunares.

Vê-se que:

primeiro, a terra lança uma sombra na lua, e a lua lança uma sombra na terra
então a lua sai da sombra da terra, e a sombra da lua sai da superfície da terra
então a sombra da lua retorna à superfície da terra e a lua entra novamente na sombra da terra
o limite entre os lados do dia e da noite da lua não é visível quando a lua é coberta pelo disco da Terra, porque o lado da lua que está de frente para nós ainda está na sombra da Terra

Na animação: o movimento das fronteiras entre os lados diurno e noturno da Terra e da Lua combinado com eclipses solar e lunar. Os caras que servem os observatórios no ponto Lagrange L2 em nosso mundo veem aproximadamente a mesma imagem) Claro, se negligenciarmos a rotação da Terra)

Foto: amanhecer na ISS em nosso mundo)

Conclusão

Para que serve tudo isso)? Eu realmente queria ver o mundo através dos olhos de uma criatura vivendo em um universo compacto e fechado com geometria esférica. Conhecer este mundo maravilhoso sem os símbolos de Christoffel e coisas semelhantes, permanecendo no quadro do curso geral da matemática superior. O resultado está na sua frente. Tudo parece dar certo. Espero que você tenha tido um dia interessante e agradável!

Código fonte

Modelo de trabalho (aberto no PC, não para dispositivos móveis).

Para aqueles que estão interessados no assunto, há um artigo magnífico que fala sobre os incríveis fenômenos que podem ser observados no universo real: como desenhar um buraco negro. Rastreamento de raios geodésicos no espaço-tempo curvo .

O mundo da hiperesfera tridimensional. Rastreamento de raios geodésicos em um universo fechado com geometria esférica

1. Introdução Mundo fechado bidimensional

Mundo fechado tridimensional

Modelo

Primeiro conhecido

Estudo visual

Conclusão

More articles: