👨🏼‍🤝‍👨🏻 💦 🕛 Logística da ação para coleta seletiva de materiais recicláveis 🛀🏿 🕺🏾 👨‍✈️

Em vez de se juntar

Quando os processos de coleta e processamento de resíduos estão totalmente ajustados na Rússia, não é fácil dizer, mas quero não participar da reposição de aterros sanitários agora. Portanto, em muitas cidades grandes, de uma maneira ou de outra, existem movimentos voluntários envolvidos em uma coleta separada particular.

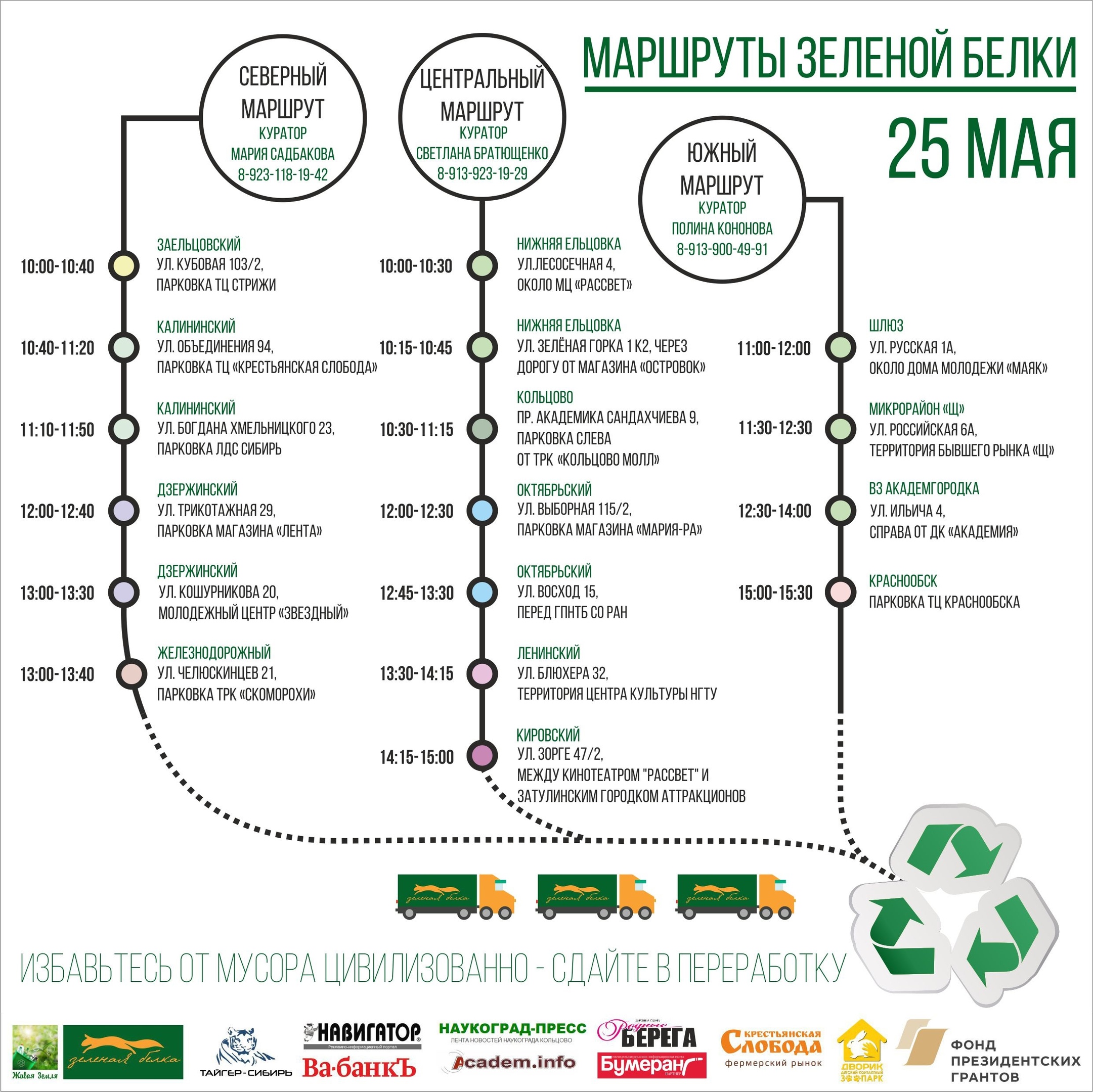
Em Novosibirsk, essa atividade é formada em torno da campanha Esquilo Verde, na qual uma vez por mês as pessoas da cidade ambiental trazem lixo doméstico reciclável acumulado para locais predeterminados em um determinado momento. Ao mesmo tempo, chega um caminhão alugado, que leva os materiais recicláveis coletados e classificados para o local, de onde é redistribuído entre várias empresas de processamento. A ação existe desde 2014 e, desde então, o número de pontos de coleta de recicláveis, bem como seus volumes, aumentou significativamente. Para o roteamento de caminhões, apenas um olhar não era suficiente e começamos a desenvolver modelos de otimização para minimizar os custos de transporte. O primeiro desses modelos é o assunto deste artigo.

Na seção 1, descreverei em detalhes e com ilustrações o esquema para organizar a ação. Além disso, na Seção 2, a tarefa de minimizar os custos de transporte será formalizada como a tarefa de rotear veículos heterogêneos com problemas de roteamento de veículos da frota com janelas de tempo. A Seção 3 é dedicada à solução desse problema usando um pacote distribuído gratuitamente para solucionar problemas de programação matemática linear inteira mista GLPK.

1. A ação "esquilo verde"

Desde 2014, o grupo de iniciativa Living Earth realiza uma campanha mensal para separar a coleção de esquilo verde reciclado em Novosibirsk. No momento da redação deste artigo, a reciclagem com várias reservas é aceita como lixo plástico rotulado como PET, PE, PP, PS, vidro, alumínio, ferro, eletrodomésticos, papel usado e muito mais. Mais de 50 voluntários participam da preparação e condução da ação. A ação não é comercial, a participação é gratuita e não implica recompensa monetária.

Pontos

A ação é realizada em 17 pontos da cidade, localizados entre si a distâncias percorridas pelo carro em um período de 15 a 90 minutos. Um desses pontos na foto: bolsas à esquerda ao longo da parede para coletar várias frações de plástico, à direita - um caminhão, no qual tudo será carregado no futuro, e no centro - um voluntário com ouvidos.

imagem

Todas as atividades no momento são organizadas por curadores que têm restrições no horário em que estão prontos para cumprir suas funções. Ao planejar uma ação, os curadores relatam o intervalo de tempo dentro do qual a ação deve passar no momento.

Há também dados sobre os volumes médios de recicláveis coletados em cada ponto.

Rotas

Os pontos são organizados em rotas que são conduzidas sucessivamente por um caminhão. Os movimentos do caminhão são monitorados pelos supervisores de rota que monitoram o ambiente operacional e tomam decisões sobre o manuseio de eventos especiais.

imagem

Caminhões

São alugados de maneira comum no âmbito de propostas de aluguel por hora de veículos de carga. Não é possível compactar o plástico no local, portanto, o principal parâmetro que caracteriza o caminhão é o volume da carroceria. A capacidade de carga no nosso caso não é um fator limitante.

Os principais gastos da ação estão relacionados ao pagamento do aluguel de caminhões, portanto, sua redução é fundamental para a existência e desenvolvimento de nossa participação, que adquire importância institucional no sentido de formar idéias sobre consumo responsável. A seguir, será descrita uma abordagem para resolver esse problema, com base na aplicação de métodos discretos de otimização, a saber, programação matemática.

2. Formalização

Ao construir o modelo matemático, permaneceremos dentro da estrutura de programas lineares inteiros mistos, para os quais é suficiente o conhecimento da álgebra da classe 7.

A única dificuldade pode ser associada ao uso de sinais abstratos de notação e soma em fórmulas. Espero que isso não afaste os leitores que têm encontros pouco frequentes com textos matemáticos.

No modelo de otimização, quatro componentes podem ser distinguidos:

a formação de grupos de pontos que compõem uma rota separada;
definição de um circuito para cada um dos grupos;
atender aos requisitos para a hora de chegada do caminhão em cada ponto;
determinação do tipo de caminhão necessário para atender a cada uma das rotas.

Consideramos cada uma das partes, introduzindo a notação necessária conforme necessário.

Agrupamento de pontos

Vamos

V = \ {1, \ pontos, n \}

$V = \ {1, \ pontos, n \}$ existem muitos índices de pontos de coleta de materiais recicláveis, e o local onde os materiais recicláveis são transportados - vamos chamá-lo de depósito - tem um índice de 0. Coloque

\ bar {V} = V \ xícara \ {0 \}

$\ bar {V} = V \ xícara \ {0 \}$

Cada grupo de pontos forma uma rota separada. Através de

R

$R$ denotar o conjunto de números de rota.

Deixe a quantidade

z_{i r}, i i n I, r i n R

$z_ {ir}, i \ in I, r \ in R$ é igual a um se o ponto

i

$i$ incluído na rota com o número

r

$r$ e zero caso contrário. Então a exigência de que o ponto

i e m V

$i \ em V$ deve entrar em uma das rotas pode ser escrito como

s u m_{r i n R} z_{i r} = z_{i 1} + z_{i 2} + p o n t o s + z_{i n} = 1.

$\ sum_ {r \ in R} z_ {ir} = z_ {i1} + z_ {i2} + \ pontos + z_ {in} = 1.$

O depósito deve inserir todas as rotas:

z_{0 r} = 1, r e m R

$z_ {0r} = 1, r \ em R$

Sutilezas

Infelizmente, esse registro cria problemas computacionais associados à simetria da região admissível. Isso pode ser eliminado com a adição de várias restrições, garantindo a escolha da decomposição lexicograficamente mínima. Você pode ler mais sobre isso em russo, por exemplo, aqui .

1 - z_{i r} l e q s u m_{j = 1}^{i - 1} l e f t (1 - s u m_{k = 1}^{r - 1} z_{j k} r i g h t) + s u m_{k = 1}^{r - 1} z_{i k}, q u a d i e m I, r e m R, r l e q i .

$1-z_ {ir} \ leq \ sum_ {j = 1} ^ {i-1} \ left (1- \ sum_ {k = 1} ^ {r-1} z_ {jk} \ right) + \ sum_ { k = 1} ^ {r-1} z_ {ik}, \ quad i \ em I, r \ em R, r \ leq i.$

Definição de desvio

As rotas são uma sequência alternada de pontos e cruzamentos entre elas. Formalmente, todos começam em um dos pontos do conjunto

V

$V$ e terminar no depósito, no entanto, será mais fácil assumir que todas as rotas são cíclicas. Essa suposição não muda a essência, mas torna todos os vértices iguais: nesse caso, não há vértices finais, todos são de trânsito.

Por pontos

i, j i n b a r V

$i, j \ in \ bar {V}$ e rota

$inline$ configurar uma variável

x_{i j r}

$x_ {ijr}$ igual a um se na rota com número

r

$r$ caminhão se movendo do ponto

i

$i$ direto ao ponto

j

$j$ e zero caso contrário.

Então exigimos, em primeiro lugar, que o caminhão se mova ao longo da rota

$inline$ visitou o ponto

i e m V

$i \ em V$ se ela, depois de se dividir em grupos, pertencer ao grupo com o número

r

$r$ :

s u m_{j i n b a r V} x_{j i r} = z_{i r}, q u a d i i n b a r V, r e m R .

$\ sum_ {j \ in \ bar {V}} x_ {jir} = z_ {ir}, \ quad i \ in \ bar {V}, r \ em R.$

Em segundo lugar, o caminhão depois de chegar ao ponto

i i n b a r V

$i \ in \ bar {V}$ deve deixá-la.

s u m_{j i n b a r V} x_{j i r} = s u m_{j i n b a r V} x_{i j r}, q u a d i i n b a r V, r e m R .

$\ sum_ {j \ in \ bar {V}} x_ {jir} = \ sum_ {j \ in \ bar {V}} x_ {ijr}, \ quad i \ in \ bar {V}, r \ em R .$

Você pode perceber que essas restrições permitem que as quantidades

x_{i j r}

$x_ {ijr}$ Defina rotas que são um conjunto de loops disjuntos. É claro que rotas desse tipo não fazem sentido e são necessárias várias restrições para evitar isso.

Sobre como eliminar sub-motocicletas

Uma maneira poderia ser a introdução de quantidades não negativas auxiliares

f_{i j r}, i, j i n b a r V, r e m R

$f_ {ijr}, i, j \ in \ bar {V}, r \ em R$ O conjunto de relações registradas usando essas quantidades elimina combinações de valores

x_{i j r}

$x_ {ijr}$ definindo rotas que não são um loop conectado.

s u m_{i i n V} f_{0 j r} = s u m_{i i n V} z_{i r}, q u a d r i n R,

$\ sum_ {i \ in V} f_ {0jr} = \ sum_ {i \ in V} z_ {ir}, \ quad r \ in R,$

f_{i j r} l e q n x_{i j r}, q u a d i i n b a r V, j i n b a r V, r i n R,

$f_ {ijr} \ leq nx_ {ijr}, \ quad i \ in \ bar {V}, j \ in \ bar {V}, r \ in R,$

s u m_{j i n b a r V} f_{j i r} = s u m_{j i n b a r V} f_{i j r} + z_{i r}, q u a d i i n V, r i n R .

$\ sum_ {j \ in \ bar {V}} f_ {jir} = \ sum_ {j \ in \ bar {V}} f_ {ijr} + z_ {ir}, \ quad i \ in V, r \ in R.$

Essas proporções especificam o fluxo do depósito para o restante dos pontos da rota. Em cada ponto intermediário, uma unidade de fluxo é absorvida; portanto, para que a rede tenha um fluxo de energia igual ao número de pontos menos um, é necessário que a rota seja conectada.

Satisfazer os requisitos no momento da chegada do caminhão em cada ponto

Em outras palavras, você precisa visitar pontos apenas dentro das janelas de tempo indicadas pelos curadores. Através de

B_{i}

$B_i$ e

E_{i}

$E_i$ denotam, respectivamente, o início e o fim do intervalo de tempo em que o curador do ponto

i

$i$ pode participar.

Para acompanhar a implementação dessas restrições, precisamos de informações sobre o tempo gasto pelo caminhão durante paradas e travessias na rota. Através de

L_{i}, i i n V

$L_i, i \ in V$ denotar a duração do carregamento no ponto

i

$i$ e através

D_{i j}, i, j i n b a r V

$D_ {ij}, i, j \ in \ bar {V}$ - tempo de mudança de um ponto

i

$i$ direto ao ponto

j

$j$ Fazemos uma reserva que

D_{0 i} = 0

$D_ {0i} = 0$ para todos

i i n b a r V

$i \ in \ bar {V}$ e geralmente pode ser executado

D_{i j} n e q D_{j i}

$D_ {ij} \ neq D_ {ji}$ para qualquer

i n e q j

$i \ neq j$

Introduzimos variáveis não negativas

a_{i}, i i n b a r V

$a_i, i \ in \ bar {V}$ e

w_{i r}, i i n b a r V, r e m R

$w_ {ir}, i \ in \ bar {V}, r \ em R$ igual aos tempos de chegada e de espera no ponto

i

$i$ ao dirigir por uma rota

r

$r$ , respectivamente. Para os valores inseridos, as seguintes relações devem ser satisfeitas.

O tempo de espera não pode ser menor que o tempo necessário para carregar

w_{i r} g e q L_{i} z_{i r}, q u a d i i n b a r V, r e m R,

$w_ {ir} \ geq L_iz_ {ir}, \ quad i \ in \ bar {V}, r \ em R,$

e igual a zero se o ponto não pertencer à rota

r

$r$

w_{i r} l e q M z_{i r}, q u a d i i n b a r V, r e m R,

$w_ {ir} \ leq Mz_ {ir}, \ quad i \ in \ bar {V}, r \ em R,$

Hora de chegada ao ponto

j

$j$ calculado em momentos apropriados para o ponto anterior

i

$i$ Aqui está uma constante bastante grande

M

$M$ usado para eliminar dependências desnecessárias ao mover-se entre

i

$i$ e

j

$j$ não feito.

a_{i} + s u m_{r i n R} w_{i r} + D_{i j} l e q a_{j} + M (1 - s u m_{r i n R} x_{i j r}), q u a d i i n I, j e m V,

$a_i + \ sum_ {r \ in R} w_ {ir} + D_ {ij} \ leq a_j + M (1 - \ sum_ {r \ in R} x_ {ijr}), \ quad i \ in I, j \ em V,$

A chegada e partida do caminhão deve estar dentro do intervalo indicado pelo curador.

a_{i} g e q B_{i}, q u a d i e m V,

$a_i \ geq B_i, \ quad i \ em V,$

a_{i} + s u m_{r i n R} w_{i r} l e q E_{i}, q u a d i e m V .

$a_i + \ sum_ {r \ in R} w_ {ir} \ leq E_i, \ quad i \ em V.$

Determinando o tipo de caminhão necessário para atender a cada rota
Indique os vários tipos de caminhões disponíveis para aluguel por

T

$T$ Tipo de caminhão

t e m T

$t \ em T$ caracterizado pelo volume corporal

C_{t}

$C_t$ e o custo do aluguel de uma hora

P_{t}

$P_t$ Tempo mínimo de aluguel de caminhão

t

$t$ denotado por

U_{t}^{0}

$U_t ^ 0$ A quantidade de recicláveis coletados no ponto

i e m V

$i \ em V$ denotado por

G_{i}

$G_i$

Introduzimos variáveis

y_{t r}, t e m T, r e m R

$y_ {tr}, t \ em T, r \ em R$ igual a um se tipo de caminhão

t

$t$ atribuído à rota de serviço com o número

r

$r$ e zero caso contrário.

Variáveis inteiras

u_{t r}, t e m T, r e m R

$u_ {tr}, t \ em T, r \ em R$ definir a hora de alugar um tipo de caminhão

t

$t$ servindo a rota com número

r

$r$
Para cada rota,

$inline$ , você deve atribuir o tipo de caminhão:

s u m_{t i n T} y_{t r} = 1, q u a d r e m R

$\ sum_ {t \ in T} y_ {tr} = 1, \ quad r \ em R$

De acordo com a divisão dos pontos entre as rotas, algumas rotas podem se tornar triviais, ou seja, conter apenas depósitos. Se a rota

r

$r$ não trivial, o caminhão atribuído a ele é alugado pelo menos

U_{t}^{0}

$U_t ^ 0$ horas.

u_{t r} g e q U_{t}^{0} (y_{t r} - s u m_{i i n V} z_{i r}), q u a d t e m T, r e m R .

$u_ {tr} \ geq U_t ^ 0 (y_ {tr} - \ sum_ {i \ in V} z_ {ir}), \ quad t \ em T, r \ em R.$

Ao mesmo tempo, a duração do contrato também deve exceder a duração total do estacionamento e da movimentação ao longo da rota.

u_{t r} g e q s u m_{i i n V} s u m_{j i n b a r V} D_{i j} x_{i j r} + s u m_{i i n b a r V} w_{i r} - M (1 - y_{t r}), q u a d r e m R, t e m T .

$u_ {tr} \ geq \ sum_ {i \ in V} \ sum_ {j \ in \ bar {V}} D_ {ij} x_ {ijr} + \ sum_ {i \ in \ bar {V}} w_ { ir} -M (1-y_ {tr}), \ quad r \ em R, t \ em T.$

Adicione restrições ao fornecimento da propriedade: se o caminhão for do tipo

t

$t$ não atribuído a uma rota

r

$r$ , seu tempo de aluguel é zero.

u_{t r} l e q M y_{t r} .

$u_ {tr} \ leq My_ {tr}.$

Todos os materiais recicláveis coletados nos pontos de rota devem caber na parte traseira do caminhão.

s u m_{i i n V} G_{i} z_{i r} l e q s u m_{t i n T} C_{t} y_{t r}, q u a d r e m R .

$\ sum_ {i \ in V} G_iz_ {ir} \ leq \ sum_ {t \ in T} C_ty_ {tr}, \ quad r \ em R.$

Finalmente, nosso objetivo é minimizar o custo do aluguel de caminhões, que, usando as designações introduzidas, é escrito como

s u m_{t i n T} s u m_{r i n R} P_{t} u_{t r}

$\ sum_ {t \ in T} \ sum_ {r \ in R} P_tu_ {tr}$

Procure uma solução

É fácil verificar se todas as expressões envolvidas no modelo de otimização são funções lineares das variáveis; portanto, para encontrar soluções exatas e aproximadas, você pode usar pacotes padrão para resolver problemas de programação inteira mista, como Gurobi , CPLEX , Xpress , ORtools , SCIP , BLIS , etc.
Escrevemos um modelo para minimizar os custos de transporte na linguagem GMPL. Isso nos permitirá usar o pacote GLPK gratuito para nossos propósitos. Para escrever código e depurar o modelo, será conveniente fazer o download do ambiente de desenvolvimento do GUSEK , que já contém GLPK em sua composição.

O GUSEK fica assim:

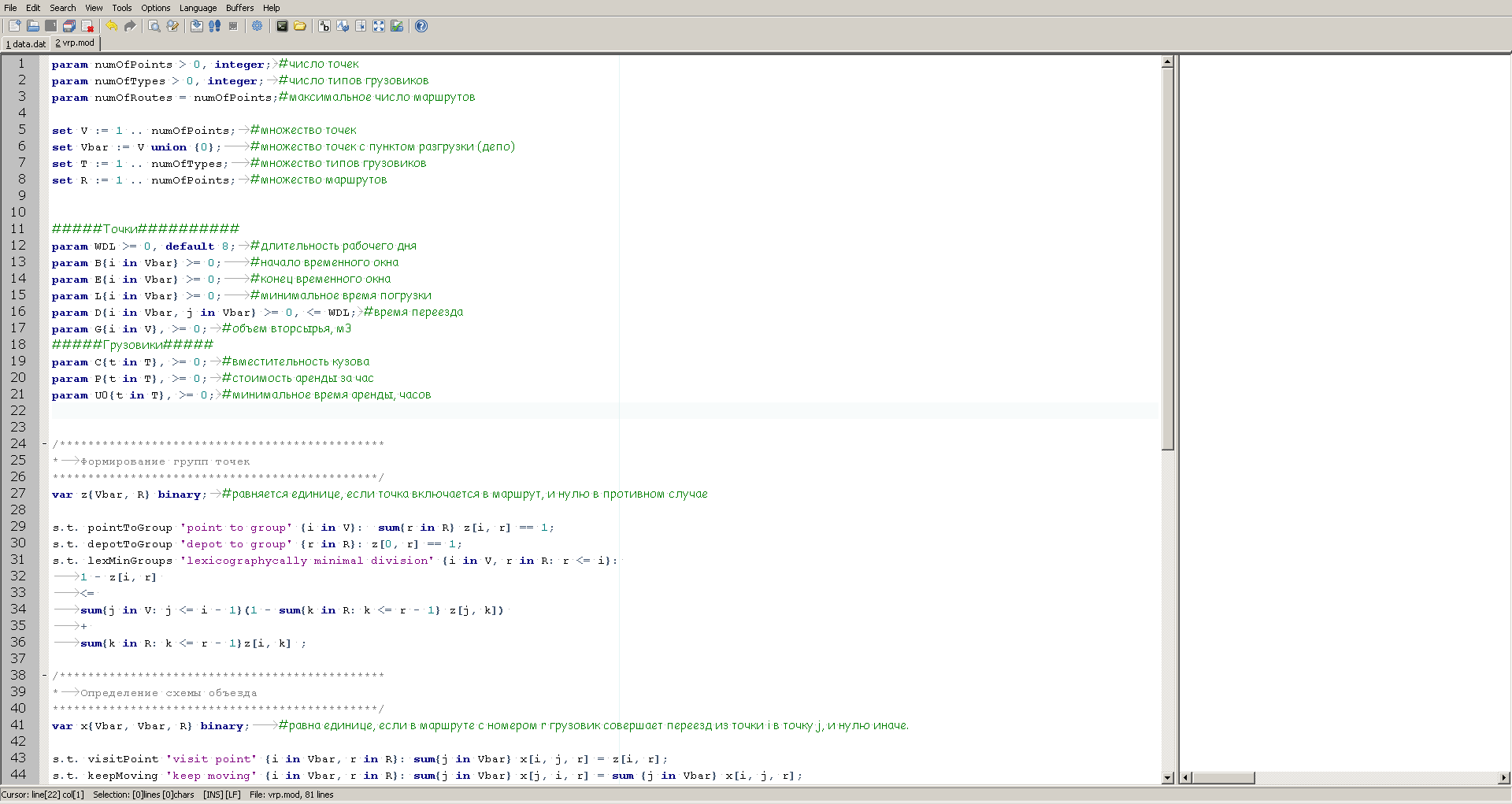
imagem

À esquerda, vemos uma descrição do modelo e à direita há uma janela para exibir informações sobre o progresso do cálculo, que o solucionador fornecerá após o lançamento.

Descrição completa do modelo

param numOfPoints > 0, integer; #  param numOfTypes > 0, integer; #   param numOfRoutes = numOfPoints;#   set V := 1 .. numOfPoints; #  set Vbar := V union {0}; #     () set T := 1 .. numOfTypes; #   set R := 1 .. numOfPoints; #  ############### param WDL >= 0, default 8; #   param B{i in Vbar} >= 0; #   param E{i in Vbar} >= 0; #   param L{i in Vbar} >= 0; #   param D{i in Vbar, j in Vbar} >= 0, <= WDL; #  param G{i in V}, >= 0; # , 3 ########## param C{t in T}, >= 0; #  param P{t in T}, >= 0; #    param U0{t in T}, >= 0; #  ,  /********************************************** *    **********************************************/ var z{Vbar, R} binary; # ,     ,      st pointToGroup 'point to group' {i in V}: sum{r in R} z[i, r] == 1; st depotToGroup 'depot to group' {r in R}: z[0, r] == 1; st lexMinGroups 'lexicographycally minimal division' {i in V, r in R: r <= i}: 1 - z[i, r] <= sum{j in V: j <= i - 1}(1 - sum{k in R: k <= r - 1} z[j, k]) + sum{k in R: k <= r - 1}z[i, k] ; /********************************************** *    **********************************************/ var x{Vbar, Vbar, R} binary; # ,    c  r      i   j,   . st visitPoint 'visit point' {i in Vbar, r in R}: sum{j in Vbar} x[i, j, r] = z[i, r]; st keepMoving 'keep moving' {i in Vbar, r in R}: sum{j in Vbar} x[j, i, r] = sum {j in Vbar} x[i, j, r]; var f{Vbar, Vbar, R} >= 0; #,  . st flowFromDepot 'flow from depot' {r in R}: sum{i in V} f[0, i, r] == sum{i in V} z[i, r]; st flowAlongActiveArcs 'flow along active arcs' {i in Vbar, j in Vbar, r in R}: f[i, j, r] <= numOfPoints * x[i, j, r]; st flowConservation 'flow conservation' {i in V, r in R}: sum{j in Vbar} f[j, i, r] == sum{j in Vbar} f[i, j, r] + z[i, r]; var a{i in V} >= 0; #     var w{i in Vbar, r in R} >= 0; #     st wait 'wait'{i in Vbar, r in R}: w[i, r] >= L[i] * z[i, r]; st dontWait 'dont wait'{i in Vbar, r in R}: w[i, r] <= (E[i] - B[i]) * z[i, r]; st arrivalTime 'arrival time' {i in V, j in V}: a[i] + sum{r in R}w[i, r] + D[i,j] <= a[j] + 3 * WDL * (1 - sum{r in R} x[i, j, r]); st arriveAfter 'arrive after' {i in V}: a[i] >= B[i]; st departBefore 'depart before' {i in V}: a[i] + sum{r in R}w[i, r] <= E[i]; /********************************************** *   ,       **********************************************/ var y{t in T, r in R}, binary; # ,    t       r,   . var u{t in T, r in R}, integer, >= 0; #    t,     rst assignVehicle 'assign vehicle' {r in R}: sum{t in T} y[t,r] == 1; st rentTime 'rent time' {r in R, t in T}: u[t, r] >= sum{i in V, j in Vbar}D[i, j] * x[i, j, r] + sum{i in Vbar}w[i, r] - WDL * (1 - y[t, r]); st minRentTime 'minimal rent time' {r in R, t in T}: u[t, r] >= U0[t] * (y[t, r] - sum{i in V}z[i, r]); st noRent 'no rent' {t in T, r in R}: u[t, r] <= WDL * y[t, r]; st fitCapacity 'fit capacity' {r in R}: sum{i in V} G[i] * z[i, r] <= sum{t in T} C[t] * y[t, r]; minimize rentCost: sum{t in T, r in R} P[t] * u[t, r]; solve; /********************************************** *     **********************************************/ printf{i in V, r in R} (if 0.1 < z[i,r] then "point %s to group %s\n" else ""), i, r, z[i,r]; printf{r in R, i in Vbar, j in Vbar} (if 0.1 < x[i, j, r] then "route %s: %s -> %s\n" else ""), r, i, j; printf{i in V} "point %s arrive between %s and %s (actual = %s)\n", i, B[i], E[i], a[i]; end;

Para começar rapidamente, também adicionarei dados da minha cabeça preparados para uso no modelo:

Dados de entrada

 data; param numOfPoints := 9; #  param numOfTypes := 6; #   ############### param : B E L := 0 0 8 1 1 0 8 1 2 0 8 1 3 0 8 1 4 0 8 1 5 0 8 1 6 0 8 1 7 0 8 1 8 0 8 1 9 0 8 1; param D default 0 : 0 1 2 3 4 5 6 7 8 9 := 0 . . . . . . . . . . 1 0.1 0.3 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 2 0.3 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 3 0.4 0.3 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 4 0.4 0.4 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 5 0.1 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 6 0.5 0.5 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 7 0.3 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 8 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1 9 0.5 0.2 0.2 0.1 0.2 0.1 0.2 0.1 0.2 0.1; param G := 1 1 2 2 3 1 4 2 5 1 6 2 7 1 8 2 9 1; ########## param : C P := 1 8 500 2 10 500 3 14 600 4 18 650 5 25 700 6 35 800; param U0 default 2; #  ,  end;

Depois de copiar o código do modelo para um arquivo com o nome, por exemplo, model.mod e os dados de entrada no arquivo data.dat, tudo estará pronto para ser executado. Definimos um limite para o tempo de cálculo de 100 segundos (isso é feito usando a tecla --tmlim [tempo em segundos]), transferimos o caminho para o arquivo com dados de entrada (usando a tecla -d [caminho do arquivo]),

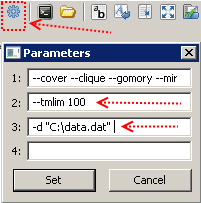
imagem

e pressione F5. Se for bem-sucedida, as mensagens aparecerão na janela à direita e, após cem segundos, teremos a melhor solução que o GLPK conseguiu encontrar no tempo previsto.

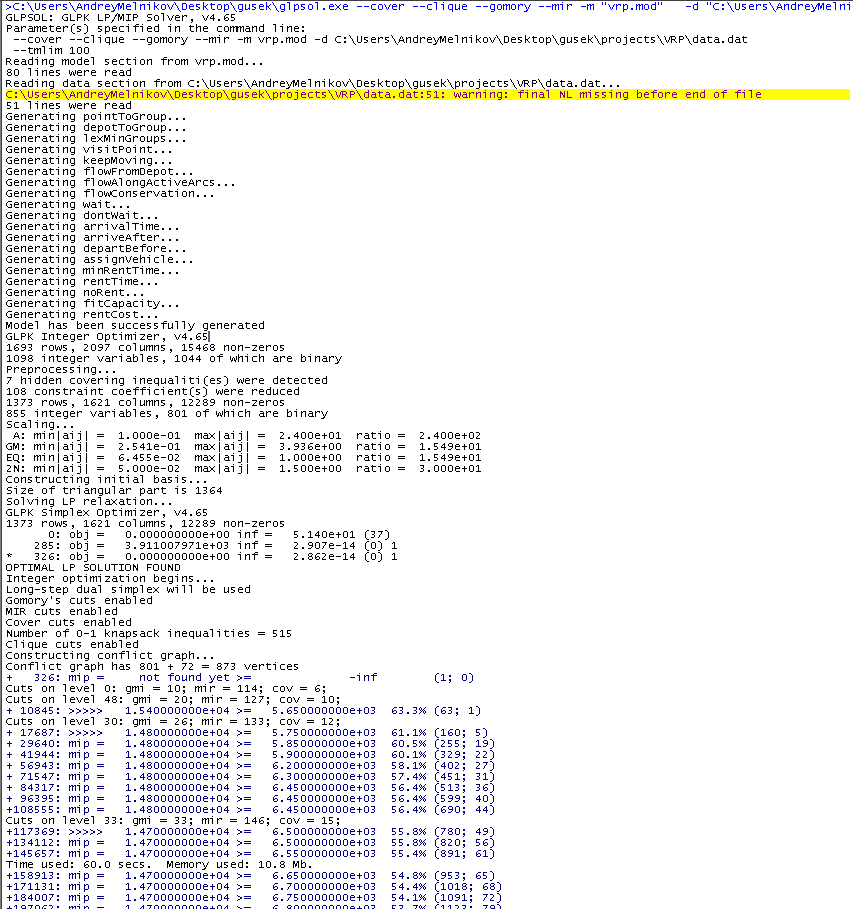
imagem

No texto em azul, estamos interessados no significado após a inscrição "mip =". Como você pode ver, diminui de tempos em tempos. Todas as novas soluções estão em processo de trabalho, cujo valor dos custos de transporte, na melhor das hipóteses, é exibido nesta coluna (existem 14700 até o momento). O próximo número é o limite inferior para a melhor solução existente, ou seja, a melhor . Inicialmente, a estimativa é subestimada significativamente, mas é refinada ao longo do tempo, ou seja, aumenta. Os valores à esquerda e à direita estão convergindo e a diferença relativa entre eles no momento da captura de tela é de 54,1%. Assim que esse número se tornar zero, o algoritmo provará que a melhor solução encontrada é a melhor possível. Nem sempre se justifica esperar por esse evento na prática, e não apenas porque é muito tempo, mas é importante fazer uma reserva de que, via de regra, uma boa solução é relativamente rápida, e os principais custos de tempo estão associados ao refinamento da estimativa necessária para provar o melhor possível.

Em vez de uma conclusão

Os problemas de roteamento são extremamente complexos em termos computacionais e, com o aumento do número de pontos que precisam ser visitados, o tempo que leva para um solucionador encontrar uma solução e provar que sua otimização está crescendo rapidamente. No entanto, para exemplos bastante pequenos, em um período de tempo razoável, o solucionador é capaz de construir um conjunto de rotas bem-sucedido e pode ser usado para apoiar a tomada de decisões. A análise das opções de roteamento propostas pelo modelo nos ajudou a descobrir oportunidades significativas de redução de custos, e isso é fundamental para a existência e o desenvolvimento do estoque.

Nossos esforços adicionais foram direcionados ao trabalho com incerteza nos volumes de recicláveis coletados nos pontos. Estamos desenvolvendo vários modelos de programação estocástica para tomar decisões estratégicas e operacionais no roteamento de caminhões. Se o tópico for relevante e despertar interesse, escreverei sobre isso também, porque em breve todos nós teremos que mergulhar significativamente mais profundamente nas questões ambientais, e é nisso que eu desejo sucesso.

Logística da ação para coleta seletiva de materiais recicláveis

Em vez de se juntar

1. A ação "esquilo verde"

2. Formalização

Procure uma solução

Em vez de uma conclusão

More articles: