Redes neurais e aprendizagem profunda, capítulo 1: usando redes neurais para reconhecer números manuscritos

Nota

Aqui está uma tradução do livro on-line gratuito de Michael Nielsen, Neural Networks and Deep Learning, distribuído sob a Licença Unported Creative Commons Attribution-NonCommercial 3.0 . A motivação para sua criação foi a experiência bem-sucedida da tradução de um livro didático de programação, o Expressive JavaScript . O livro sobre redes neurais também é bastante popular: autores de artigos em inglês o citam ativamente. Não encontrei as traduções dela, exceto a tradução do começo do primeiro capítulo com abreviações .

Quem quiser agradecer ao autor do livro pode fazer isso em sua página oficial , por transferência via PayPal ou Bitcoin. Para apoiar o tradutor em Habré, existe um formulário "para apoiar o autor".

1. Introdução

Este tutorial apresentará detalhes sobre conceitos como:

• Redes neurais - um excelente paradigma de software, criado sob a influência da biologia e permitindo que o computador aprenda com base em observações.
• O aprendizado profundo é um poderoso conjunto de técnicas de treinamento em redes neurais.

As redes neurais (NS) e o aprendizado profundo (GO) hoje oferecem a melhor solução para muitos problemas nas áreas de reconhecimento de imagem, processamento de voz e linguagem natural. Este tutorial ensinará muitos dos principais conceitos que sustentam o NS e o GO.

Sobre o que é este livro

O NS é um dos melhores paradigmas de software já inventados pelo homem. Com uma abordagem de programação padrão, dizemos ao computador o que fazer, dividimos grandes tarefas em muitas pequenas e determinamos com precisão as tarefas que o computador executará facilmente. No caso da Assembléia Nacional, pelo contrário, não dizemos ao computador como resolver o problema. Ele mesmo aprende isso com base em "observações" dos dados, "inventando" sua própria solução para o problema.

O aprendizado automatizado baseado em dados parece promissor. No entanto, até 2006, não sabíamos como treinar a Assembléia Nacional para que eles pudessem transcender as abordagens mais tradicionais, com exceção de alguns casos especiais. Em 2006, técnicas de treinamento dos chamados redes neurais profundas (GNS). Agora, essas técnicas são conhecidas como aprendizado profundo (GO). Eles continuaram sendo desenvolvidos e hoje o GNS e o GO alcançaram resultados surpreendentes em muitas tarefas importantes relacionadas à visão por computador, reconhecimento de fala e processamento de linguagem natural. Em larga escala, eles estão sendo implantados por empresas como Google, Microsoft e Facebook.

O objetivo deste livro é ajudá-lo a dominar os principais conceitos de redes neurais, incluindo técnicas modernas de GO. Depois de trabalhar com o tutorial, você escreverá um código que usa NS e GO para resolver problemas complexos de reconhecimento de padrões. Você terá uma base para usar o NS e a defesa civil na abordagem para resolver seus próprios problemas.

Abordagem Baseada em Princípios

Uma das crenças subjacentes ao livro é que é melhor adquirir uma sólida compreensão dos princípios-chave da Assembléia Nacional e da Sociedade Civil do que obter conhecimento de uma longa lista de idéias diferentes. Se você tiver um bom entendimento das ideias-chave, entenderá rapidamente outro material novo. Na linguagem do programador, podemos dizer que estudaremos a sintaxe básica, as bibliotecas e as estruturas de dados da nova linguagem. Você pode reconhecer apenas uma pequena fração de todo o idioma - muitos idiomas têm imensas bibliotecas padrão - no entanto, é possível entender novas bibliotecas e estruturas de dados de maneira rápida e fácil.

Portanto, este livro não é categoricamente material educacional sobre como usar qualquer biblioteca específica para a Assembléia Nacional. Se você quer apenas aprender a trabalhar com a biblioteca - não leia o livro! Encontre a biblioteca que você precisa e trabalhe com materiais e documentação de treinamento. Mas lembre-se: embora essa abordagem tenha a vantagem de solucionar o problema instantaneamente, se você quiser entender exatamente o que está acontecendo dentro da Assembléia Nacional, se quiser dominar idéias que serão relevantes em muitos anos, não será suficiente apenas estudar algumas biblioteca de moda. Você precisa entender as idéias confiáveis ​​e de longo prazo subjacentes ao trabalho da Assembléia Nacional. A tecnologia vem e vai, e as idéias duram para sempre.

Abordagem prática

Estudaremos os princípios básicos pelo exemplo de uma tarefa específica: ensinar um computador a reconhecer números manuscritos. Usando abordagens de programação tradicionais, essa tarefa é extremamente difícil de resolver. No entanto, podemos resolvê-lo muito bem com um NS simples e várias dezenas de linhas de código, sem nenhuma biblioteca especial. Além disso, melhoraremos gradualmente esse programa, incluindo consistentemente nele mais e mais idéias importantes sobre a Assembléia Nacional e a Defesa Civil.

Essa abordagem prática significa que você precisará de alguma experiência em programação. Mas você não precisa ser um programador profissional. Eu escrevi o código python (versão 2.7) que deve ficar claro mesmo se você não tiver escrito programas python. No processo de estudo, criaremos nossa própria biblioteca para a Assembléia Nacional, que você poderá usar para experimentos e treinamento adicional. Todo o código pode ser baixado aqui . Depois de terminar o livro, ou no processo de leitura, você pode escolher uma das bibliotecas mais completas para a Assembléia Nacional, adaptada para uso nesses projetos.

Os requisitos matemáticos para entender o material são bastante médios. A maioria dos capítulos possui partes matemáticas, mas geralmente são álgebra elementar e gráficos de funções. Às vezes, uso matemática mais avançada, mas estruturei o material para que você possa entendê-lo, mesmo que alguns detalhes lhe escapem. A maior parte da matemática é usada no capítulo 2, que requer um pouco de análise analítica e álgebra linear. Para aqueles a quem eles não estão familiarizados, começo o capítulo 2 com uma introdução à matemática. Se você achar difícil, pule o capítulo até o interrogatório. De qualquer forma, não se preocupe com isso.

Um livro raramente é ao mesmo tempo orientado para a compreensão de princípios e uma abordagem prática. Mas acredito que é melhor estudar com base nas idéias fundamentais da Assembléia Nacional. Vamos escrever código de trabalho, e não apenas estudar a teoria abstrata, e você pode explorar e estender esse código. Dessa forma, você entenderá o básico, tanto a teoria quanto a prática, e poderá aprender mais.

Exercícios e tarefas

Os autores de livros técnicos geralmente alertam o leitor que ele simplesmente precisa concluir todos os exercícios e resolver todos os problemas. Ao ler esses avisos para mim, eles sempre parecem um pouco estranhos. Algo ruim vai acontecer comigo se eu não realizar exercícios e resolver problemas? Não é claro. Apenas economizarei tempo com uma compreensão menos profunda. Às vezes vale a pena. Às vezes não.

O que vale a pena fazer com este livro? Aconselho que você tente concluir a maioria dos exercícios, mas não tente resolver a maioria das tarefas.

A maioria dos exercícios precisa ser concluída, pois são verificações básicas para o entendimento adequado do material. Se você não pode executar o exercício com relativa facilidade, deve ter perdido algo fundamental. Claro, se você está realmente preso a algum tipo de exercício - deixe de lado, talvez isso seja algum tipo de pequeno mal-entendido, ou talvez eu tenha formulado algo mal. Mas se a maioria dos exercícios lhe causar dificuldades, é provável que você precise reler o material anterior.

Tarefas são outra questão. Eles são mais difíceis do que exercícios, e com alguns você terá dificuldade. Isso é irritante, mas é claro que a paciência diante de tanta decepção é a única maneira de realmente entender e absorver o assunto.

Portanto, eu não recomendo resolver todos os problemas. Melhor ainda - escolha seu próprio projeto. Você pode usar o NS para classificar sua coleção de músicas. Ou para prever o valor dos estoques. Ou algo mais. Mas encontre um projeto interessante para você. E então você pode ignorar as tarefas do livro ou usá-las apenas como inspiração para trabalhar em seu projeto. Problemas com seu próprio projeto ensinam mais do que trabalhar com inúmeras tarefas. O envolvimento emocional é um fator chave na conquista do domínio.

Obviamente, embora você não tenha um projeto como esse. Isso é normal. Resolva tarefas para as quais você sente motivação intrínseca. Use o material do livro para ajudá-lo a encontrar idéias para projetos criativos pessoais.

Capítulo 1

O sistema visual humano é uma das maravilhas do mundo. Considere a seguinte sequência de números manuscritos:



A maioria das pessoas os lê com facilidade, como 504192. Mas essa simplicidade é enganadora. Em cada hemisfério do cérebro, uma pessoa tem um córtex visual primário , também conhecido como V1, que contém 140 milhões de neurônios e dezenas de bilhões de conexões entre eles. Ao mesmo tempo, não apenas a V1 está envolvida na visão humana, mas toda uma sequência de regiões do cérebro - V2, V3, V4 e V5 - envolvidas no processamento de imagens cada vez mais complexo. Temos em nossas cabeças um supercomputador sintonizado pela evolução por centenas de milhões de anos e perfeitamente adaptado para entender o mundo visível. Reconhecer números manuscritos não é tão fácil. É que nós, surpreendentemente, surpreendentemente bem, reconhecemos o que nossos olhos nos mostram. Mas quase todo esse trabalho é realizado inconscientemente. E geralmente não atribuímos importância à tarefa difícil que nossos sistemas visuais resolvem.

A dificuldade de reconhecer padrões visuais se torna aparente quando você tenta escrever um programa de computador para reconhecer números como os acima. O que parece fácil em nossa execução de repente acaba sendo extremamente complexo. O conceito simples de como reconhecemos as formas - “o nove tem um loop no topo e a barra vertical no canto inferior direito” - não é tão simples para uma expressão algorítmica. Ao tentar articular essas regras claramente, você rapidamente fica preso em um atoleiro de exceções, armadilhas e ocasiões especiais. A tarefa parece sem esperança.

Abordagem NS para resolver o problema de uma maneira diferente. A idéia é pegar os muitos números manuscritos conhecidos como exemplos de ensino,



e desenvolver um sistema que possa aprender com esses exemplos. Em outras palavras, a Assembléia Nacional usa exemplos para construir automaticamente regras de reconhecimento de dígitos manuscritas. Além disso, aumentando o número de exemplos de treinamento, a rede pode aprender mais sobre números manuscritos e melhorar sua precisão. Portanto, embora eu tenha citado acima apenas 100 estudos de caso, talvez possamos criar um melhor sistema de reconhecimento de escrita usando milhares ou mesmo milhões e bilhões de estudos de caso.

Neste capítulo, escreveremos um programa de computador que implementa o NS aprendendo a reconhecer números manuscritos. O programa terá apenas 74 linhas e não utilizará bibliotecas especiais para a Assembléia Nacional. No entanto, este pequeno programa poderá reconhecer números manuscritos com uma precisão de mais de 96%, sem a necessidade de intervenção humana. Além disso, em capítulos futuros, desenvolveremos idéias que podem melhorar a precisão para 99% ou mais. De fato, os melhores NSs comerciais fazem um trabalho tão bom que são usados ​​pelos bancos para processar cheques e o serviço postal para reconhecer endereços.

Nós nos concentramos no reconhecimento de manuscrito, pois esse é um grande protótipo de uma tarefa para o estudo da NS. Esse protótipo é ideal para nós: é uma tarefa difícil (reconhecer números manuscritos não é uma tarefa fácil), mas não é tão complicado que requer uma solução extremamente complexa ou imenso poder de computação. Além disso, essa é uma ótima maneira de desenvolver técnicas mais complexas, como o GO. Portanto, no livro, retornaremos constantemente à tarefa de reconhecimento de manuscrito. Posteriormente discutiremos como essas idéias podem ser aplicadas a outras tarefas de visão computacional, reconhecimento de fala, processamento de linguagem natural e outras áreas.

Obviamente, se o objetivo deste capítulo fosse apenas escrever um programa para reconhecer números manuscritos, o capítulo seria muito mais curto! No entanto, no processo, desenvolveremos muitas idéias-chave relacionadas ao SN, incluindo dois tipos importantes de neurônios artificiais ( perceptron e neurônio sigmóide) e o algoritmo padrão de aprendizado do NS, a descida do gradiente estocástico . No texto, concentro-me em explicar por que tudo é feito dessa maneira e em moldar sua compreensão da Assembléia Nacional. Isso requer uma conversa mais longa do que se eu tivesse acabado de apresentar a mecânica básica do que está acontecendo, mas custa um entendimento mais profundo que você terá. Entre outras vantagens - até o final do capítulo, você entenderá o que é uma defesa civil e por que é tão importante.

Perceptrons

O que é uma rede neural? Para começar, falarei sobre um tipo de neurônio artificial chamado perceptron. Os Perceptrons foram inventados pelo cientista Frank Rosenblatt nos anos 50 e 60, inspirados nos primeiros trabalhos de Warren McCallock e Walter Pitts . Hoje, outros modelos de neurônios artificiais são usados ​​com mais frequência - neste livro, e a maioria dos trabalhos modernos sobre NS usam principalmente o modelo sigmóide do neurônio. Nós a encontraremos em breve. Mas, para entender por que os neurônios sigmóides são definidos dessa maneira, vale a pena gastar tempo analisando o perceptron.

Então, como os perceptrons funcionam? O perceptron recebe vários números binários x ₁ , x ₂ , ... e fornece um número binário:



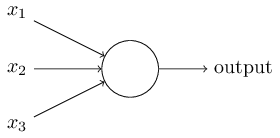
Neste exemplo, o perceptron possui três números de entrada, x ₁ , x ₂ , x ₃ . Em geral, pode haver mais ou menos deles. Rosenblatt propôs uma regra simples para o cálculo do resultado. Ele introduziu pesos, w ₁ , w ₂ , números reais, expressando a importância dos números de entrada correspondentes para os resultados. A saída de um neurônio, 0 ou 1, é determinada pelo fato de uma soma ponderada ser menor ou maior que um determinado limiar [limiar] $$$\ sum_j w_jx_j$ . Como pesos, o limiar é um número real, um parâmetro de um neurônio. Em termos matemáticos:

$$

$$output = \ begin {cases} 0 ~ se ~ \ sum_j w_jx_j \ limite de leq \\ 1 ~ if ~ \ sum_j w_jx_j> limite \ end {cases} \ tag {1}$$

Essa é a descrição completa do perceptron!

Este é o modelo matemático básico. Um perceptron pode ser pensado como um tomador de decisão, pesando as evidências. Deixe-me dar um exemplo não muito realista, mas simples. Digamos que o fim de semana está chegando, e você ouviu que um festival de queijos será realizado em sua cidade. Você gosta de queijo e tenta decidir se vai ao festival ou não. Você pode tomar uma decisão ponderando três fatores:

1. O tempo está bom?
2. Seu parceiro quer ir com você?
3. O festival está longe do transporte público? (Você não tem carro).

Esses três fatores podem ser representados como variáveis ​​binárias x ₁ , x ₂ , x ₃ . Por exemplo, x ₁ = 1 se o tempo estiver bom e 0 se estiver ruim. x ₂ = 1 se o seu parceiro deseja ir e 0 se não. Mesmo para x ₃ .

Agora, digamos que você é tão fã de queijo que está pronto para ir ao festival, mesmo que seu parceiro não esteja interessado e seja difícil chegar a ele. Mas talvez você odeie o mau tempo e, em caso de mau tempo, não irá ao festival. Você pode usar o perceptrons para modelar esse processo de tomada de decisão. Uma maneira é escolher o peso w ₁ = 6 para o clima e w ₂ = 2, w ₃ = 2 para outras condições. Um valor maior de w ₁ significa que o tempo importa muito mais para você do que se o seu parceiro irá acompanhá-lo ou a proximidade do festival para uma parada. Finalmente, suponha que você selecione o limite 5. Para o perceptron. Com essas opções, o perceptron implementa o modelo de decisão desejado, fornecendo 1 quando o tempo está bom e 0 quando está ruim. O desejo do parceiro e a proximidade da parada não afetam o valor da saída.

Ao alterar pesos e limites, podemos obter diferentes modelos de tomada de decisão. Por exemplo, digamos que aceitamos o limiar 3. Então o perceptron decide que você precisa ir ao festival, quando o tempo está bom ou quando o festival está perto de uma parada de ônibus e seu parceiro concorda em ir com você. Em outras palavras, o modelo é diferente. Baixar o limiar significa que você deseja ir mais ao festival.

Obviamente, o perceptron não é um modelo completo de tomada de decisão humana! Mas este exemplo mostra como um perceptron pode pesar diferentes tipos de evidência para tomar decisões. Parece possível que uma rede complexa de perceptrons possa tomar decisões muito complexas:



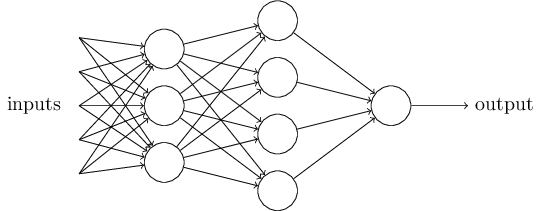
Nesta rede, a primeira coluna de perceptrons - o que chamamos de primeira camada de perceptrons - toma três decisões muito simples, ponderando as evidências de entrada. E os perceptrons da segunda camada? Cada um deles toma uma decisão, avaliando os resultados da primeira camada de tomada de decisão. Dessa maneira, o perceptron da segunda camada pode tomar uma decisão em um nível mais complexo e abstrato em comparação com o perceptron da primeira camada. E decisões ainda mais complexas podem ser tomadas por perceptrons na terceira camada.Dessa maneira, uma rede multicamada de perceptrons pode lidar com decisões complexas.

A propósito, quando determinei o perceptron, eu disse que ele tinha apenas um valor de saída. Mas na rede no topo, os perceptrons parecem ter vários valores de saída. De fato, eles têm apenas uma saída. Muitas setas de saída são apenas uma maneira conveniente de mostrar que a saída do perceptron é usada como entrada de vários outros perceptrons. Isso é menos complicado do que desenhar uma única saída ramificada.

Vamos simplificar a descrição dos perceptrons. Condição$$Σ j de w j x j > t r um e s h o l d estranho, e que pode concordar em duas mudanças para a gravação da sua simplicidade. O primeiro é gravar$\sum_j w_jx_j > treshold$$$Σ j de w j x j como o produto escalar,$\sum_j w_jx_j$$$w ⋅ x = Σ j w j x j , em que w e x - um vector, cujos componentes são o peso e os dados de entrada, respectivamente. O segundo é transferir o limiar para outra parte da desigualdade e substituí-lo por um valor conhecido como deslocamento de perceptron [viés],$w \cdot x = \sum_j w_jx_j$$$$b \equiv −threshold$ . Usando deslocamento em vez de um limite, podemos reescrever a regra do perceptron:

$$

$$output = \begin{cases} 0 ~ if ~ w \cdot x + b \leq 0 \\ 1 ~ if ~ w \cdot x + b > 0 \end{cases} \tag{2}$$

O deslocamento pode ser representado como uma medida de quão fácil é obter um valor de 1 na saída do perceptron. Ou, em termos biológicos, o deslocamento é uma medida de quão fácil é obter o perceptron para ativar. Um perceptron com um viés muito grande é extremamente fácil de fornecer 1. Mas com um viés negativo muito grande, isso é difícil de executar. Obviamente, a introdução do viés é uma pequena mudança na descrição dos perceptrons, mas mais tarde veremos que isso leva a uma maior simplificação da gravação. Portanto, ainda não usaremos o limite, mas sempre usaremos o deslocamento.

Descrevi perceptrons em termos do método de pesar evidências para a tomada de decisão. Outro método de uso é o cálculo de funções lógicas elementares, que geralmente consideramos os principais cálculos, como AND, OR e NAND. Suponha, por exemplo, que tenhamos um perceptron com duas entradas, o peso de cada uma das quais é -2 e seu deslocamento é 3. Aqui está: A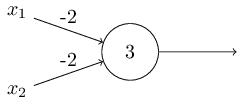



entrada 00 fornece a saída 1, porque (−2) ∗ 0 + (- 2 ) ∗ 0 + 3 = 3 é maior que zero. Os mesmos cálculos dizem que as entradas 01 e 10 dão 1. Mas 11 na entrada dá 0 na saída, pois (−2) ∗ 1 + (- 2) ∗ 1 + 3 = −1, menor que zero. Portanto, nosso perceptron implementa a função NAND!

Este exemplo mostra que perceptrons podem ser usados ​​para calcular funções lógicas básicas. De fato, podemos usar redes perceptron para calcular quaisquer funções lógicas em geral. O fato é que o portão lógico NAND é universal para cálculos - é possível construir qualquer cálculo com base em ele. Por exemplo, você pode usar portas NAND para criar um circuito que adiciona dois bits, x ₁ e x ₂ . Para fazer isso, calcule a soma bit a bit$$x 1 ⊕ x 2 , bem comoo sinalizador de transporte, que é 1 quando ambos x₁e x₂são 1 - ou seja, o sinalizador de transporte é simplesmente o resultado da multiplicação por bits x₁x₂:Para obter a rede equivalente de perceptrons, substituímos todos As portas NAND são perceptrons com duas entradas, o peso de cada uma delas é -2 e com um deslocamento de 3. Aqui está a rede resultante. 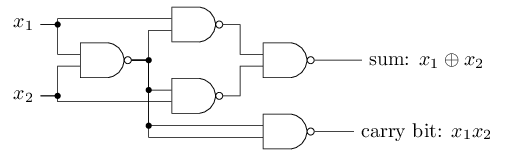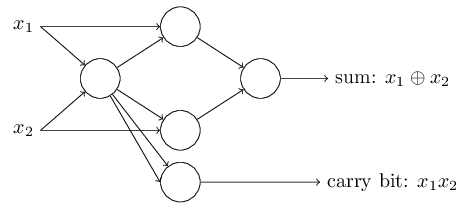Observe que movi o perceptron correspondente à válvula inferior direita, apenas para tornar mais conveniente desenhar setas:$x_1 \oplus x_2$







Um aspecto digno de nota dessa rede perceptron é que a saída da mais à esquerda é usada duas vezes como entrada na parte inferior. Definindo o modelo do perceptron, não mencionei a admissibilidade de um esquema de saída dupla no mesmo local. De fato, isso realmente não importa. Se não queremos permitir isso, podemos simplesmente combinar duas linhas com pesos de -2 em uma com um peso de -4. (Se isso não lhe parecer óbvio, pare e prove para si mesmo). Após essa alteração, a rede tem a seguinte aparência, com todos os pesos não alocados iguais a -2, todos os deslocamentos iguais a 3 e um peso -4 é marcado:



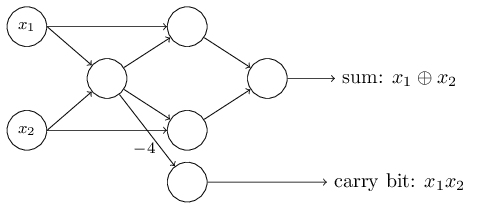Esse registro de perceptrons que possuem uma saída, mas sem entradas:



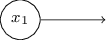é apenas uma abreviação. Isso não significa que ele não tem entradas. Para entender isso, suponha que tenhamos um perceptron sem entradas. Então a soma ponderada ∑ _j w _j x _j sempre seria zero, portanto o perceptron daria 1 para b> 0 e 0 para b ≤ 0. Ou seja, o perceptron daria apenas um valor fixo, e não o que precisamos (x ₁ no exemplo acima). É melhor considerar os perceptrons de entrada não como perceptrons, mas como unidades especiais que são simplesmente definidas de modo a produzir os valores desejados x ₁ , x ₂ , ...

O exemplo do somador demonstra como uma rede perceptron pode ser usada para simular um circuito contendo muitos portões NAND. E como esses portões são universais para cálculos, portanto, os perceptrons são universais para cálculos.

A versatilidade computacional dos perceptrons é encorajadora e decepcionante. É encorajador, garantir que a rede perceptron possa ser tão poderosa quanto qualquer outro dispositivo de computação. Decepcionante, dando a impressão de que perceptrons são apenas um novo tipo de porta lógica NAND. Descoberta mais ou menos!

No entanto, a situação é realmente melhor. Acontece que podemos desenvolver algoritmos de treinamento que podem ajustar automaticamente os pesos e deslocamentos da rede dos neurônios artificiais. Esse ajuste ocorre em resposta a estímulos externos, sem a intervenção direta de um programador. Esses algoritmos de aprendizado nos permitem usar neurônios artificiais de uma maneira radicalmente diferente dos portões lógicos comuns. Em vez de registrar explicitamente um circuito de portas NAND e outros, nossas redes neurais podem simplesmente aprender a resolver problemas, às vezes aqueles para os quais seria extremamente difícil projetar diretamente um circuito regular.

Neurônios sigmóides

Os algoritmos de aprendizado são ótimos. No entanto, como desenvolver esse algoritmo para uma rede neural? Suponha que tenhamos uma rede de perceptrons que queremos usar para nos treinar na solução de um problema. Suponha que a entrada na rede possa ser pixels de uma imagem digitalizada de um dígito manuscrito. E queremos que a rede conheça os pesos e compensações necessárias para classificar corretamente os números. Para entender como esse treinamento pode funcionar, vamos imaginar que estamos mudando um pouco de peso (ou viés) na rede. Queremos que essa pequena alteração leve a uma pequena alteração na saída da rede. Como veremos em breve, essa propriedade torna possível o aprendizado. Esquematicamente, queremos o seguinte (obviamente, essa rede é muito simples para reconhecer a escrita à mão!):



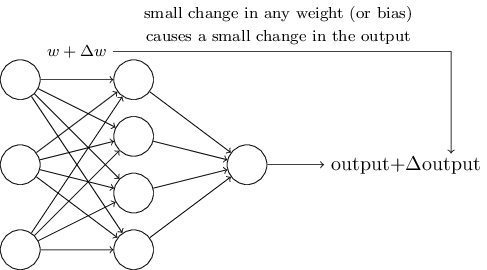
Se uma pequena alteração no peso (ou viés) levasse a uma pequena alteração no resultado da saída, poderíamos alterar os pesos e os desvios para que nossa rede se comporte um pouco mais perto do que queremos. Por exemplo, digamos que a rede atribuiu incorretamente a imagem a "8", embora devesse ter sido a "9". Poderíamos descobrir como fazer uma pequena alteração no peso e no deslocamento para que a rede se aproxime um pouco mais da classificação da imagem como “9”. E então repetiríamos isso, alterando pesos e mudanças várias vezes para obter o melhor e o melhor resultado. A rede aprenderia.

O problema é que, se houver perceptrons na rede, isso não acontece. Uma pequena mudança nos pesos ou deslocamento de qualquer perceptron pode às vezes levar a uma mudança na sua saída para o oposto, digamos, de 0 a 1. Essa mudança pode mudar o comportamento do resto da rede de uma maneira muito complicada. E mesmo que agora o nosso "9" seja corretamente reconhecido, o comportamento da rede com todas as outras imagens provavelmente mudou completamente de uma maneira que é difícil de controlar. Por isso, é difícil imaginar como podemos ajustar gradualmente pesos e compensações para que a rede se aproxime gradualmente do comportamento desejado. Talvez haja uma maneira inteligente de contornar esse problema. Mas não há uma solução simples para o problema de aprender uma rede de perceptrons.

Esse problema pode ser contornado com a introdução de um novo tipo de neurônio artificial chamado neurônio sigmóide. Eles são semelhantes aos perceptrons, mas modificados para que pequenas alterações nos pesos e compensações resultem em apenas pequenas alterações na saída. Esse é um fato básico que permitirá que a rede de neurônios sigmóides aprenda.

Deixe-me descrever um neurônio sigmóide. Vamos desenhá-los da mesma maneira que perceptrons:



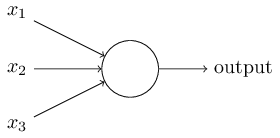
Possui a mesma entrada x ₁ , x ₂ , ... Mas, em vez de serem iguais a 0 ou 1, essas entradas podem ter qualquer valor no intervalo de 0 a 1. Por exemplo, um valor de 0,638 será uma entrada válida para neurônio sigmóide (CH). Assim como o perceptron, o SN tem pesos para cada entrada, w ₁ , w ₂ , ... e o viés total b. Mas seu valor de saída não será 0 ou 1. Ele será σ (w⋅x + b), onde σ é o sigmóide.

A propósito, σ às vezes é chamado de função logística , e essa classe de neurônios é chamada de neurônios logísticos. É útil lembrar dessa terminologia, pois esses termos são usados ​​por muitas pessoas que trabalham com redes neurais. No entanto, aderiremos à terminologia sigmóide.

A função é definida da seguinte maneira:

$$

$$\ sigma (z) \ equiv \ frac {1} {1 + e ^ {- z}} \ tag {3}$$

No nosso caso, o valor de saída do neurônio sigmóide com dados de entrada x ₁ , x ₂ , ... pelos pesos w ₁ , w ₂ , ... e deslocamento b será considerado como:

$$

$$\ frac {1} {1 + exp (- \ sum_j w_jx_j - b)} \ tag {4}$$

À primeira vista, o CH parece completamente diferente dos neurônios. A aparência algébrica de um sigmóide pode parecer confusa e obscura se você não estiver familiarizado com ele. De fato, existem muitas semelhanças entre perceptrons e SN, e a forma algébrica de um sigmóide acaba sendo mais um detalhe técnico do que uma séria barreira à compreensão.

Para entender as semelhanças com o modelo perceptron, suponha que z ≡ w ⋅ x + b seja um número positivo grande. Então e - z ≈ 0, portanto, σ (z) ≈ 1. Em outras palavras, quando z = w ⋅ x + b é grande e positivo, o rendimento SN é aproximadamente 1, como no perceptron. Suponha que z = w ⋅ x + b seja grande com um sinal de menos. Então e - z → ∞ e σ (z) ≈ 0. Portanto, para z grande com sinal de menos, o comportamento do SN também se aproxima do perceptron. E somente quando w ⋅ x + b tem um tamanho médio, há sérios desvios do modelo de perceptron observado.

E a forma algébrica de σ? Como o entendemos? De fato, a forma exata de σ não é tão importante - a forma da função no gráfico é importante. Aqui está:



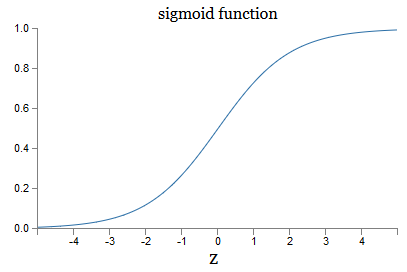
Esta é uma versão suave da função step:



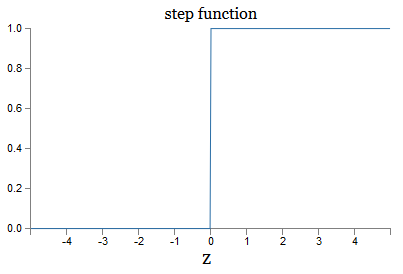
Se σ fosse escalonado, o SN seria um perceptron, pois teria saída 0 ou 1 dependendo do sinal w ⋅ x + b (bem, de fato, em z = 0, o perceptron fornece 0 e a função step 1 , portanto, nesse ponto, a função precisaria ser alterada).

Usando a função real σ, obtemos um perceptron suavizado. E o principal aqui é a suavidade da função, não sua forma exata. Suavidade significa que pequenas alterações Δw _j pesos e δb deslocamentos fornecerão pequenas alterações Δde saída da saída. A álgebra nos diz que a saída é bem aproximada da seguinte maneira:

$$

$$\ Saída delta \ approx \ sum_j \ frac {\ saída parcial} {\ parcial w_j} \ Delta w_j + \ frac {\ saída parcial} {\ parcial b} \ Delta b \ tag {5}$$

Onde a soma está acima de todos os pesos wj, e ∂ saída / ∂w _j e ∂ saída / ∂b denotam as derivadas parciais da saída em relação a w _j e b, respectivamente. Não entre em pânico se você se sentir inseguro na companhia de derivativos privados! Embora a fórmula pareça complicada, com todas essas derivadas parciais, na verdade ela diz algo bastante simples (e útil): Δ Saída é uma função linear que depende dos pesos e desvios de Δw _j e Δb. Sua linearidade facilita a seleção de pequenas alterações de pesos e compensações para atingir qualquer pequeno viés de saída desejado. Portanto, embora os SNs sejam semelhantes aos perceptrons no comportamento qualitativo, eles facilitam a compreensão de como a saída pode ser alterada alterando pesos e deslocamentos.

Se a forma geral σ é importante para nós, e não sua forma exata, então por que usamos essa fórmula (3)? De fato, mais tarde consideraremos neurônios cuja saída é f (w ⋅ x + b), onde f () é outra função de ativação. O principal que muda quando a função muda é o valor das derivadas parciais na equação (5). Acontece que, quando calculamos essas derivadas parciais, o uso de σ simplifica muito a álgebra, pois os expoentes têm propriedades muito boas ao diferenciar. De qualquer forma, σ é frequentemente usado no trabalho com redes neurais e, mais frequentemente, neste livro, usaremos essa função de ativação.

Como interpretar o resultado do trabalho de CH? Obviamente, a principal diferença entre os perceptrons e o CH é que o CH não fornece apenas 0 ou 1. Sua saída pode ser qualquer número real de 0 a 1, portanto valores como 0,173 ou 0,669 são válidos. Isso pode ser útil, por exemplo, se você desejar que o valor de saída indique, por exemplo, o brilho médio dos pixels da imagem recebidos na entrada do NS. Mas, às vezes, pode ser inconveniente. Suponha que queremos que a saída de rede diga que “a imagem 9 foi inserida” ou “a imagem de entrada não é 9”. Obviamente, seria mais fácil se os valores de saída fossem 0 ou 1, como um perceptron. Mas, na prática, podemos concordar que qualquer valor de saída de pelo menos 0,5 significaria "9" na entrada e qualquer valor menor que 0,5 significaria que "não é 9". Eu sempre indicarei explicitamente a existência de tais acordos.

Exercícios

• CH simulando perceptrons, parte 1

Suponha que tomemos todos os pesos e compensações de uma rede de perceptrons e os multipliquemos por uma constante positiva c> 0. Mostre que o comportamento da rede não muda.

• CH simulando perceptrons, parte 2

Suponha que tenhamos a mesma situação do problema anterior - uma rede de perceptrons. Suponha também que os dados de entrada para a rede estejam selecionados. Não precisamos de um valor específico, o principal é que ele seja fixo. Suponha que os pesos e deslocamentos sejam tais que w⋅x + b b 0, onde x é o valor de entrada de qualquer percepção da rede. Agora substituímos todos os perceptrons na rede por SN e multiplicamos os pesos e deslocamentos pela constante positiva c> 0. Mostre que no limite c → ∞ o comportamento da rede a partir do SN será exatamente o mesmo que as redes de perceptrons. Como esta afirmação será violada se, para um dos perceptrons, w⋅x + b = 0?

Arquitetura de rede neural

Na próxima seção, apresentarei uma rede neural capaz de uma boa classificação de números manuscritos. Antes disso, é útil explicar a terminologia que nos permite apontar para diferentes partes da rede. Digamos que temos a seguinte rede:



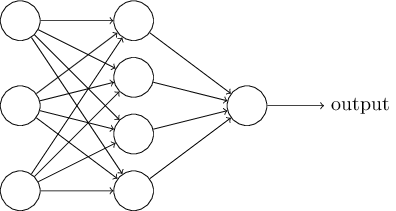
Como mencionei, a camada mais à esquerda na rede é chamada de camada de entrada e seus neurônios são chamados de neurônios de entrada. A camada mais à direita, ou saída, contém neurônios de saída ou, como no nosso caso, um neurônio de saída. A camada do meio é chamada oculta, porque seus neurônios não são entrada nem saída. O termo "oculto" pode parecer um pouco misterioso - quando o ouvi pela primeira vez, decidi que deveria ter uma profunda importância filosófica ou matemática - no entanto, significa apenas "não entrar nem sair". A rede acima tem apenas uma camada oculta, mas algumas redes têm várias camadas ocultas. Por exemplo, na rede de quatro camadas a seguir, existem duas camadas ocultas:



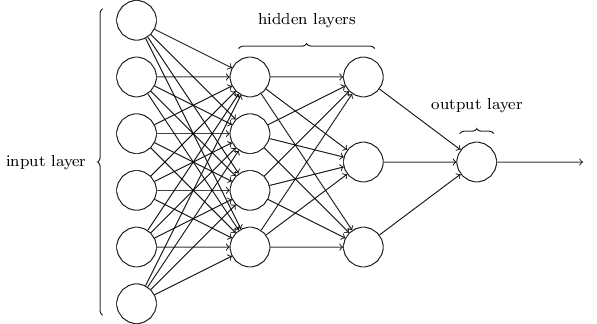
Isso pode ser confuso, mas, por razões históricas, essas redes multicamadas são algumas vezes chamadas de perceptrons multicamadas, MLPs, apesar de consistirem em neurônios sigmóides e não em perceptrons. Não vou usar essa terminologia porque é confusa, mas devo advertir sobre sua existência.

Projetar camadas de entrada e saída às vezes é uma tarefa simples. Por exemplo, digamos que estamos tentando determinar se o número manuscrito significa "9" ou não. Um circuito de rede natural codifica o brilho dos pixels da imagem nos neurônios de entrada. Se a imagem for em preto e branco, com 64x64 pixels de tamanho, teremos 64x64 = 4096 neurônios de entrada, com brilho no intervalo de 0 a 1. A camada de saída conterá apenas um neurônio, cujo valor menor que 0,5 significa que "em a entrada não era 9 ", mas valores mais significam que" a entrada era 9 ".

E embora projetar camadas de entrada e saída geralmente seja uma tarefa simples, projetar camadas ocultas pode ser uma arte difícil. Em particular, não é possível descrever o processo de desenvolvimento de camadas ocultas com algumas regras simples. Pesquisadores da Assembléia Nacional desenvolveram muitas regras heurísticas para o design de camadas ocultas que ajudam a obter o comportamento desejado das redes neurais. Por exemplo, essa heurística pode ser usada para entender como alcançar um compromisso entre o número de camadas ocultas e o tempo disponível para o treinamento da rede. Mais tarde, encontraremos algumas dessas regras.

Até agora, discutimos NSs em que a saída de uma camada é usada como entrada para a próxima. Tais redes são chamadas de redes neurais de distribuição direta. Isso significa que não há loops na rede - as informações sempre avançam e nunca são realimentadas. Se tivéssemos loops, encontraríamos situações nas quais a entrada sigmóide dependeria da saída. Seria difícil de entender e não permitimos esses loops.

No entanto, existem outros modelos de NSs artificiais nos quais é possível usar loops de feedback. Esses modelos são chamados de redes neurais recorrentes (RNS). A idéia dessas redes é que seus neurônios sejam ativados por períodos limitados de tempo. Essa ativação pode estimular outros nêutrons, que podem ser ativados um pouco mais tarde, também por tempo limitado. Isso leva à ativação dos seguintes neurônios e, com o tempo, obtemos uma cascata de neurônios ativados. Loops nesses modelos não apresentam problemas, uma vez que a saída de um neurônio afeta sua entrada posteriormente, e não imediatamente.

Os RNSs não foram tão influentes quanto os NSs de distribuição direta, principalmente porque os algoritmos de treinamento para RNSs até agora têm menos potencial. No entanto, o RNS ainda permanece extremamente interessante. No espírito do trabalho, eles estão muito mais próximos do cérebro do que os NS de distribuição direta. É possível que o RNS seja capaz de resolver problemas importantes que, com a ajuda da distribuição direta NS, possam ser resolvidos com grandes dificuldades. No entanto, a fim de limitar o escopo de nosso estudo, nos concentraremos no SN de distribuição direta mais amplamente utilizado.

Rede simples de classificação de tinta

Tendo definido as redes neurais, retornaremos ao reconhecimento de manuscrito. A tarefa de reconhecer números manuscritos pode ser dividida em duas subtarefas. Primeiro, queremos encontrar uma maneira de dividir uma imagem contendo muitos dígitos em uma sequência de imagens individuais, cada uma contendo um dígito. Por exemplo, gostaríamos de dividir a imagem



em seis separados



Nós, humanos, podemos resolver facilmente esse problema de segmentação, mas é difícil para um programa de computador dividir a imagem corretamente. Após a segmentação, o programa precisa classificar cada dígito individual. Por exemplo, queremos que nosso programa reconheça que o primeiro dígito



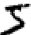
são 5.

Vamos nos concentrar na criação de um programa para resolver o segundo problema, a classificação de números individuais. Acontece que o problema da segmentação não é tão difícil de resolver assim que encontramos uma boa maneira de classificar dígitos individuais. Existem muitas abordagens para resolver o problema de segmentação. Uma delas é tentar muitas maneiras diferentes de segmentação de imagens usando o classificador de dígitos individuais, avaliando cada tentativa. A segmentação de avaliação é muito apreciada se o classificador de dígitos individuais estiver confiante na classificação de todos os segmentos e baixa se houver problemas em um ou mais segmentos. A idéia é que, se o classificador tiver problemas em algum lugar, isso provavelmente significa que a segmentação está incorreta. Essa ideia e outras opções podem ser usadas para uma boa solução para o problema de segmentação. Portanto, em vez de nos preocuparmos com a segmentação, nos concentraremos no desenvolvimento de um NS capaz de resolver uma tarefa mais interessante e complexa, a saber, o reconhecimento de números manuscritos individuais.

Para reconhecer dígitos individuais, usaremos o NS de três camadas:



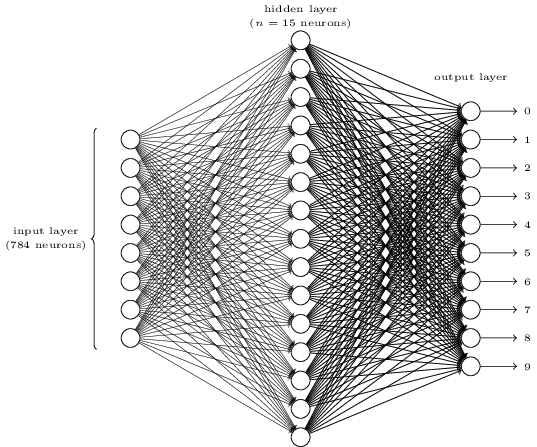
A camada da rede de entrada contém neurônios que codificam vários valores dos pixels de entrada. Como será indicado na próxima seção, nossos dados de treinamento consistirão em muitas imagens de dígitos manuscritos digitalizados com tamanho de 28x28 pixels, portanto a camada de entrada contém 28x28 = 784 neurônios. Por simplicidade, não indiquei a maioria dos 784 neurônios no diagrama. Os pixels recebidos são preto e branco, com um valor de 0,0 indicando branco, 1,0 indicando preto e valores intermediários indicando tons de cinza cada vez mais escuros.

A segunda camada da rede está oculta. Denotamos o número de neurônios nessa camada n e experimentaremos diferentes valores de n. O exemplo acima mostra uma pequena camada oculta contendo apenas n = 15 neurônios.

Existem 10 neurônios na camada de saída da rede. Se o primeiro neurônio estiver ativado, ou seja, seu valor de saída for ± 1, isso indica que a rede acredita que a entrada foi 0. Se o segundo neurônio estiver ativado, a rede acredita que a entrada foi 1. E assim por diante. A rigor, numeramos os neurônios de saída de 0 a 9 e observamos quais deles tinham o valor máximo de ativação. Se este é, digamos, o neurônio nº 6, nossa rede acredita que a entrada foi o número 6. E assim por diante.

Você pode se perguntar por que precisamos usar dez neurônios. Afinal, queremos saber qual dígito de 0 a 9 corresponde à imagem de entrada. Seria natural usar apenas 4 neurônios de saída, cada um deles com um valor binário, dependendo de seu valor de saída ser mais próximo de 0 ou 1. Quatro neurônios seriam suficientes, já que 2 ⁴ = 16, mais de 10 valores possíveis. Por que nossa rede deve usar 10 neurônios? Isso é ineficaz? A base para isso é empírica; podemos tentar as duas variantes da rede e, para essa tarefa, uma rede com 10 neurônios de saída é melhor treinada para reconhecer números do que uma rede com 4. No entanto, a questão permanece: por que 10 neurônios de saída são melhores? Existe alguma heurística que nos diga com antecedência que 10 neurônios de saída devem ser usados ​​em vez de 4?

Para entender o porquê, é útil pensar no que uma rede neural faz. Primeiro, considere a opção com 10 neurônios de saída. Nós nos concentramos no primeiro neurônio de saída, que está tentando decidir se a imagem recebida é zero. Ele faz isso pesando as evidências obtidas de uma camada oculta. O que os neurônios ocultos fazem? Suponha que o primeiro neurônio na camada oculta determine se há algo assim na figura:



Ele pode fazer isso atribuindo pesos grandes a pixels correspondentes a esta imagem e pesos pequenos ao restante. Da mesma forma, suponha que o segundo, terceiro e quarto neurônios na camada oculta procurem se existem fragmentos semelhantes na imagem:



Como você deve ter adivinhado, todos esses quatro fragmentos juntos apresentam a imagem 0, que vimos anteriormente:



Portanto, se os quatro neurônios ocultos forem ativados, podemos concluir que o número é 0. Claro, essa não é a única evidência de que 0 foi exibido lá - podemos obter 0 de muitas outras maneiras (mudando ligeiramente essas imagens ou distorcendo-as levemente). No entanto, podemos dizer com certeza que, pelo menos nesse caso, podemos concluir que havia 0 na entrada.

Se assumirmos que a rede funciona assim, podemos dar uma explicação plausível do porquê é melhor usar 10 neurônios de saída em vez de 4. Se tivéssemos 4 neurônios de saída, o primeiro neurônio tentaria decidir qual é o bit mais significativo do dígito recebido. E não há uma maneira fácil de associar o bit mais significativo aos formulários simples fornecidos acima. É difícil imaginar quaisquer razões históricas pelas quais partes da forma de um dígito estariam de alguma forma relacionadas ao bit mais significativo da saída.

No entanto, todas as opções acima são suportadas apenas por heurísticas. Nada fala a favor do fato de que uma rede de três camadas deve funcionar como eu disse, e os neurônios ocultos devem encontrar componentes simples de formas. Talvez o complicado algoritmo de aprendizado encontre pesos que nos permitam usar apenas 4 neurônios de saída. No entanto, como heurística, meu método funciona bem e pode economizar um tempo considerável no desenvolvimento de uma boa arquitetura NS.

Exercícios

• , . , . . , 3 , ( ) 0,99, 0,01.

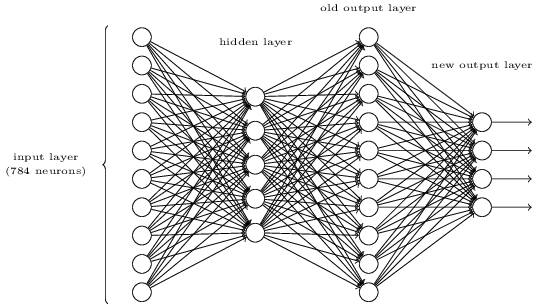Então, nós temos o esquema de NA - como aprender a reconhecer números? A primeira coisa que precisamos é treinar dados, os chamados conjunto de dados de treinamento. Usaremos o kit MNIST contendo dezenas de milhares de imagens digitalizadas de números manuscritos e sua classificação correta. O nome MNIST recebeu devido ao fato de ser um subconjunto modificado dos dois conjuntos de dados coletados pelo NIST , o Instituto Nacional de Padrões e Tecnologia dos EUA. Aqui estão algumas imagens do MNIST:



Estes são os mesmos números que foram fornecidos no início do capítulo como uma tarefa de reconhecimento. Obviamente, ao verificar o NS, solicitaremos que ela reconheça as imagens erradas que já estavam no conjunto de treinamento!

Os dados do MNIST consistem em duas partes. O primeiro contém 60.000 imagens destinadas ao treinamento. São manuscritos digitalizados de 250 pessoas, metade das quais eram funcionários do US Census Bureau e a outra metade eram estudantes do ensino médio. As imagens são em preto e branco, medindo 28x28 pixels. A segunda parte do conjunto de dados MNIST é de 10.000 imagens para testar a rede. Esta também é uma imagem em preto e branco de 28x28 pixels. Usaremos esses dados para avaliar quão bem a rede aprendeu a reconhecer números. Para melhorar a qualidade da avaliação, esses números foram extraídos de outras 250 pessoas que não participaram da gravação do conjunto de treinamento (embora também fossem funcionários do Bureau e estudantes do ensino médio). Isso nos ajuda a garantir que nosso sistema possa reconhecer a letra manuscrita de pessoas que não encontrou durante o treinamento.

A entrada de treinamento será indicada por x. Será conveniente tratar cada imagem de entrada x como um vetor com medidas 28x28 = 784. Cada valor dentro do vetor indica o brilho de um pixel na imagem. Denotaremos o valor de saída como y = y (x), onde y é um vetor de dez dimensões. Por exemplo, se uma determinada imagem de treinamento x contiver 6, y (x) = (0,0,0,0,0,0,1,0,0,0) ^T será o vetor de que precisamos. T é uma operação de transposição que transforma um vetor de linha em um vetor de coluna.

Queremos encontrar um algoritmo que permita procurar tais pesos e compensações para que a saída da rede se aproxime de y (x) para toda a entrada de treinamento x. Para quantificar a aproximação desse objetivo, definimos uma função de custo (às vezes chamada de função de perda); no livro, usaremos a função cost, mas lembre-se de outro nome):

$$

$$C(w, b) = \frac{1}{2n} \sum_x || y(x) – a ||^2 \tag{6}$$

Aqui w denota um conjunto de pesos de rede, b é um conjunto de compensações, n é o número de dados de entrada de treinamento, a é o vetor de dados de saída quando x é um dado de entrada e a soma passa por toda a entrada de treinamento x. A saída, é claro, depende de x, we eb, mas por simplicidade, não designei essa dependência. A notação || v || significa o comprimento do vetor v. Vamos chamar C de função de custo quadrático; às vezes também é chamado de erro padrão, ou MSE. Se você olhar atentamente para C, poderá ver que não é negativo, pois todos os membros da soma não são negativos. Além disso, o custo de C (w, b) se torna pequeno, ou seja, C (w, b) ≈ 0, precisamente quando y (x) é aproximadamente igual ao vetor de saída a para todos os dados de entrada de treinamento x. Portanto, nosso algoritmo funcionou bem se conseguíssemos encontrar pesos e compensações tais que C (w, b) ≈ 0. E vice-versa, funcionou mal quando C (w,b) grande - significa que y (x) não corresponde à saída para uma grande quantidade de entrada. Acontece que o objetivo do algoritmo de treinamento é minimizar o custo de C (w, b) em função de pesos e compensações. Em outras palavras, precisamos encontrar um conjunto de pesos e compensações que minimizem o valor do custo. Faremos isso usando um algoritmo chamado descida de gradiente.

Por que precisamos de um valor quadrático? Não estamos interessados ​​principalmente no número de imagens corretamente reconhecidas pela rede? É possível simplesmente maximizar esse número diretamente e não minimizar o valor intermediário do valor quadrático? O problema é que o número de imagens reconhecidas corretamente não é uma função suave dos pesos e compensações da rede. Na maioria das vezes, pequenas alterações nos pesos e deslocamentos não alteram o número de imagens reconhecidas corretamente. Por isso, é difícil entender como alterar pesos e desvios para melhorar a eficiência. Se usarmos uma função de custo suave, será fácil entender como fazer pequenas alterações nos pesos e compensações, a fim de melhorar o custo. Portanto, primeiro focaremos no valor quadrático e, em seguida, estudaremos a precisão da classificação.

Mesmo considerando que queremos usar uma função de custo suave, você ainda pode estar interessado em saber por que escolhemos a função quadrática para a equação (6)? Não é possível escolher arbitrariamente? Talvez se escolhêssemos uma função diferente, teríamos um conjunto completamente diferente de pesos e compensações minimizadores? Uma pergunta razoável e, posteriormente, examinaremos novamente a função de custo e faremos algumas correções. No entanto, a função de custo quadrático funciona muito bem para entender as coisas básicas na aprendizagem de NS, portanto, por enquanto, continuaremos com ela.

Resumindo: nosso objetivo no treinamento de NS é encontrar pesos e compensações que minimizem a função de custo quadrático C (w, b). A tarefa é bem colocada, mas até agora tem muitas estruturas que distraem - a interpretação de w e b como pesos e compensações, a função σ oculta em segundo plano, a escolha da arquitetura de rede, MNIST e assim por diante. Acontece que podemos entender muito, ignorando grande parte dessa estrutura e concentrando-nos apenas no aspecto da minimização. Então, por enquanto, esqueceremos a forma especial da função de custo, a comunicação com a Assembléia Nacional e assim por diante. Em vez disso, vamos imaginar que apenas temos uma função com muitas variáveis ​​e queremos minimizá-la. Vamos desenvolver uma tecnologia chamada descida de gradiente, que pode ser usada para resolver esses problemas. E então voltamos a uma determinada função,que queremos minimizar para a Assembléia Nacional.

Bem, digamos que estamos tentando minimizar algumas funções C (v). Pode ser qualquer função com valores reais de muitas variáveis ​​v = v ₁ , v ₂ , ... Observe que substituí a notação w e b por v para mostrar que ela pode ser qualquer função - não estamos mais obcecados com HC. É útil imaginar que uma função C tenha apenas duas variáveis ​​- v ₁ e v ₂ :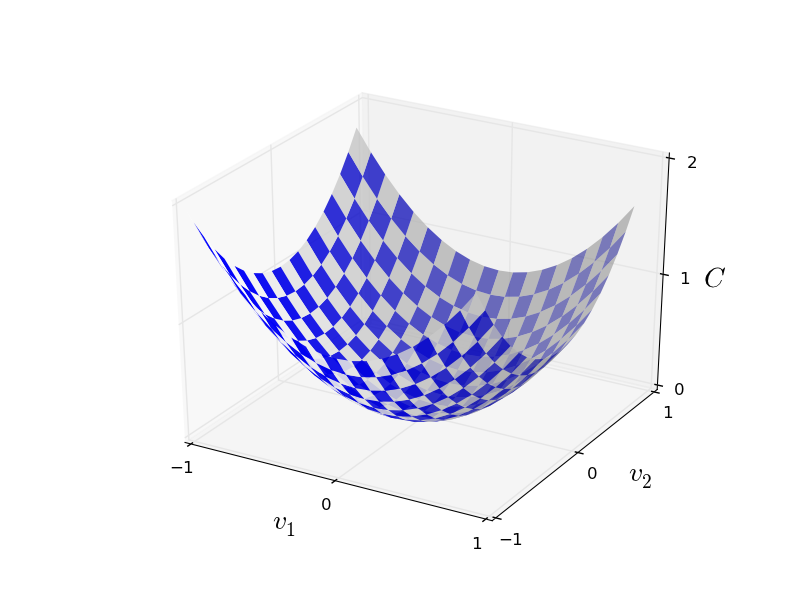



gostaríamos de descobrir onde C atinge um mínimo global. Obviamente, com a função desenhada acima, podemos estudar o gráfico e encontrar o mínimo. Nesse sentido, eu posso ter lhe dado uma função muito simples! No caso geral, C pode ser uma função complexa de muitas variáveis, e geralmente é impossível apenas olhar o gráfico e encontrar o mínimo.

Uma maneira de resolver o problema é usar a álgebra para encontrar o mínimo analiticamente. Podemos calcular as derivadas e tentar usá-las para encontrar o extremo. Se tivermos sorte, isso funcionará quando C for uma função de uma ou duas variáveis. Mas com um grande número de variáveis, isso se transforma em um pesadelo. E para os NSs, muitas vezes precisamos de muito mais variáveis ​​- para os maiores NSs, o custo funciona de maneira complexa e depende de bilhões de pesos e deslocamentos. O uso de álgebra para minimizar essas funções falhará!

(Tendo declarado que seria mais conveniente considerar C como uma função de duas variáveis, eu disse duas vezes em dois parágrafos “sim, mas e se for uma função de um número muito maior de variáveis?” Peço desculpas. Acredite, será realmente útil representar C como uma função duas variáveis, é que às vezes essa imagem se desfaz, e é por isso que os dois parágrafos anteriores foram necessários. Para o raciocínio matemático, muitas vezes é necessário manipular várias representações intuitivas, aprendendo ao mesmo tempo quando a representação pode ser usada e quando não ZYA).

Ok, isso significa que álgebra não vai funcionar. Felizmente, existe uma grande analogia que oferece um algoritmo que funciona bem. Imaginamos nossa função como algo como um vale. Com a programação mais recente, não será tão difícil de fazer. E imaginamos uma bola rolando ao longo da encosta do vale. Nossa experiência nos diz que a bola acabará deslizando para o fundo. Talvez possamos usar essa idéia para encontrar o mínimo de uma função? Selecionamos aleatoriamente o ponto de partida para uma bola imaginária e, em seguida, simulamos o movimento da bola, como se ela estivesse rolando para o fundo do vale. Podemos usar essa simulação simplesmente contando as derivadas (e, possivelmente, as segundas derivadas) de C - elas nos dirão tudo sobre a forma local do vale e, portanto, sobre como nossa bola irá rolar.

Com base no que você escreveu, você pode pensar que vamos escrever as equações de movimento de Newton para a bola, considerar os efeitos do atrito e da gravidade e assim por diante. De fato, não estaremos tão perto de seguir essa analogia com a bola - estamos desenvolvendo um algoritmo para minimizar C, e não uma simulação exata das leis da física! Essa analogia deve estimular nossa imaginação e não limitar nosso pensamento. Então, em vez de mergulhar nos detalhes complexos da física, vamos fazer a pergunta: se fôssemos nomeados deus por um dia, e criaríamos nossas próprias leis da física, dizendo à bola como aplicar qual lei ou leis de movimento escolheríamos, para que a bola sempre role fundo do vale?

Para esclarecer a questão, pensaremos no que acontece se movermos a bola uma pequena distância Δv ₁ na direção da v ₁e uma pequena distância Δv ₂ na direção de v ₂ . A álgebra nos diz que C muda da seguinte maneira:

$$

$$\Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2 \tag{7}$$

Encontraremos uma maneira de escolher tais Δv ₁ e Δv ₂ para que ΔC seja menor que zero; isto é, vamos selecioná-los para que a bola role para baixo. Para entender como fazer isso, é útil definir Δv como o vetor de alterações, ou seja, Δv ≡ (Δv ₁ , Δv ₂ ) ^T , onde T é a operação de transposição que transforma vetores de linha em vetores de coluna. Nós também definir o gradiente C como derivados parciais (∂S / ∂V ₁ , ∂S / ∂V ₂ ) ^T . Denotamos o vetor gradiente por ∇:

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2})^T \tag{8}$$

Em breve, reescreveremos a mudança de ΔC a Δv e o gradiente ∇C. Enquanto isso, quero esclarecer uma coisa, por causa da qual as pessoas costumam ficar no gradiente. Quando se encontraram pela primeira vez com ∇C, as pessoas às vezes não entendem como deveriam perceber o símbolo ∇. O que isso significa especificamente? De fato, você pode considerar com segurança ∇C um único objeto matemático - um vetor definido anteriormente - que é simplesmente escrito usando dois caracteres. Desse ponto de vista, ∇ é como acenar uma bandeira informando que "∇C é um vetor gradiente". Existem pontos de vista mais avançados dos quais ∇ pode ser considerado uma entidade matemática independente (por exemplo, como um operador de diferenciação), mas não precisamos deles.

Com essas definições, a expressão (7) pode ser reescrita como:

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{9}$$

Essa equação ajuda a explicar por que ∇C é chamado de vetor gradiente: conecta as mudanças em v com as mudanças em C, exatamente como esperado de uma entidade chamada gradiente. [eng. gradiente - desvio / aprox. transl.] No entanto, é mais interessante que essa equação nos permita ver como escolher Δv para que ΔC seja negativo. Digamos que escolhemos

$$

$$\Delta v = - \eta \nabla C \tag{10}$$

onde η é um pequeno parâmetro positivo (velocidade de aprendizado). Então a equação (9) nos diz que ΔC ≈ - η ∇C ⋅ ∇C = - η || ∇C || ² . Desde || ∇C || ² ≥ 0, isso garante que ΔC ≤ 0, ou seja, C diminua o tempo todo se mudarmos v, conforme prescrito em (10) (é claro, como parte da aproximação da equação (9)). E é exatamente disso que precisamos! Portanto, tomamos a equação (10) para determinar a "lei do movimento" da bola em nosso algoritmo de descida de gradiente. Ou seja, usaremos a equação (10) para calcular o valor de Δv e depois moveremos a bola para esse valor:

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{11}$$

Em seguida, aplicamos novamente esta regra para a próxima jogada. Continuando a repetição, baixaremos C até que, esperançosamente, alcancemos um mínimo global.

Resumindo, a descida do gradiente funciona através do cálculo seqüencial do gradiente ∇ C e subsequente deslocamento na direção oposta, o que leva a uma “queda” ao longo da encosta do vale. Isso pode ser visualizado da seguinte maneira: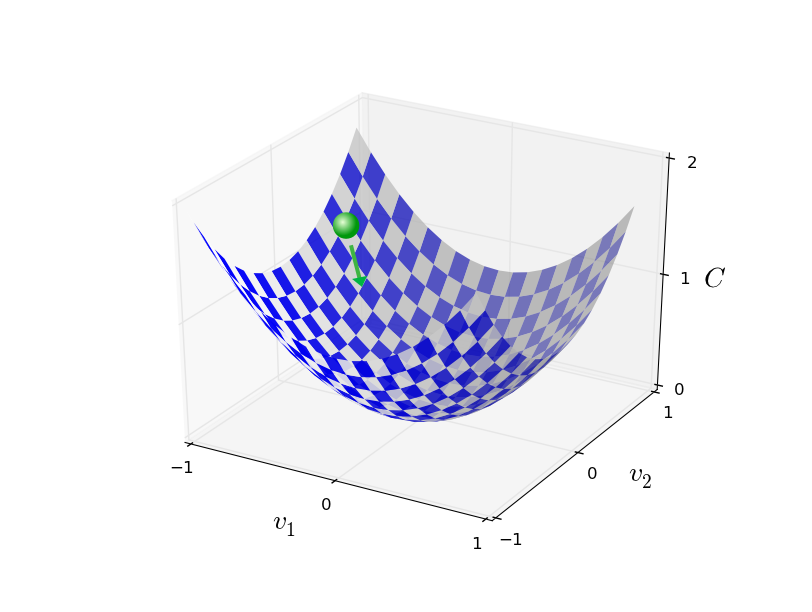



Observe que, com essa regra, a descida do gradiente não reproduz o movimento físico real. Na vida real, a bola tem um impulso que pode rolar pela encosta ou até rolar por algum tempo. Somente após o trabalho da força de atrito é que a bola rolará pelo vale. Nossa regra de seleção Δv apenas diz "desça". Uma boa regra para encontrar o mínimo!

Para que a descida do gradiente funcione corretamente, precisamos escolher um valor suficientemente pequeno da velocidade de aprendizado η para que a equação (9) seja uma boa aproximação. Caso contrário, pode resultar que ΔC> 0 - nada de bom! Ao mesmo tempo, não é necessário que η seja muito pequeno, pois as alterações em Δv serão pequenas e o algoritmo funcionará muito lentamente. Na prática, η muda para que a equação (9) forneça uma boa aproximação e o algoritmo não funcione muito lentamente. Mais tarde veremos como funciona.

Expliquei a descida do gradiente quando a função C dependia de apenas duas variáveis. Mas tudo funciona da mesma maneira se C é uma função de muitas variáveis. Suponha que ela tenha m variáveis, v ₁ , ..., v _m. Então a mudança em ΔC causada por uma pequena mudança em Δv = (Δv ₁ , ..., Δv _m ) ^T será

$$

$$\Delta C \approx \nabla C \cdot \Delta v \tag{12}$$

onde o gradiente ∇C é o vetor

$$

$$\nabla C \equiv (\frac{\partial C}{\partial v_1},…, \frac{\partial C}{\partial v_m})^T \tag{13}$$

Tal como acontece com duas variáveis, podemos escolher

$$

$$\Delta v = - \eta \nabla C \tag{14}$$

e assegure que nossa expressão aproximada (12) para ΔC seja negativa. Isso nos permite percorrer o gradiente ao mínimo, mesmo quando C é uma função de muitas variáveis, aplicando a regra de atualização repetidamente.

$$

$$v \rightarrow v' = v - \eta \nabla C \tag{15}$$

Esta regra de atualização pode ser considerada o algoritmo de descida de gradiente definidor. Ele nos fornece um método de alterar repetidamente a posição de v em busca do mínimo da função C. Essa regra nem sempre funciona - várias coisas podem dar errado, impedindo que a descida do gradiente encontre o mínimo global de C - retornaremos a esse ponto nos próximos capítulos. Mas, na prática, a descida gradiente geralmente funciona muito bem e veremos que na Assembléia Nacional essa é uma maneira eficaz de minimizar a função de custo e, portanto, treinar a rede.

Em certo sentido, a descida do gradiente pode ser considerada a melhor estratégia de pesquisa mínima. Suponha que estamos tentando mover Δv para uma posição para minimizar C. Isso é equivalente a minimizar ΔC ≈ ∇C ⋅ Δv. Limitaremos o tamanho da etapa para que || Δv || = ε para alguma constante pequena ε> 0. Em outras palavras, queremos mover uma pequena distância de tamanho fixo e tentar encontrar a direção do movimento que diminua C o máximo possível. Pode-se provar que a escolha de Δv que minimiza ∇C ⋅ Δv é Δv = -η∇C, onde η = ε / || ∇C || é determinada pela restrição || Δv || = ε. Portanto, a descida em gradiente pode ser considerada uma maneira de dar pequenos passos na direção que diminui mais a C.

Exercícios

• . : — , , , .
• , , . , ? ?

As pessoas estudaram muitas opções para a descida do gradiente, incluindo aquelas que reproduzem com mais precisão uma bola física real. Essas opções têm suas vantagens, mas também uma grande desvantagem: a necessidade de calcular as segundas derivadas parciais de C, que podem consumir muitos recursos. Para entender isso, suponha que precisamos calcular todas as segundas derivadas parciais ∂ ² C / ∂v _j ∂v _k . Se as variáveis _{vj são} milhões, precisamos calcular cerca de um trilhão (um milhão ao quadrado) das segundas derivadas parciais (na verdade, meio trilhão, uma vez que C ² C / ∂v _j ∂v _k = ∂ ² C / ∂v _k ∂v _j. Mas você pegou a essência). Isso exigirá muitos recursos de computação. Existem truques para evitar isso, e a busca de alternativas à descida do gradiente é uma área de pesquisa ativa. No entanto, neste livro, usaremos a descida gradiente e suas variantes como a principal abordagem para o aprendizado da SN.

Como aplicamos a descida gradiente ao aprendizado de NA? Precisamos usá-lo para procurar pesos _wk e deslocamentos b _l que minimizem a equação de custo (6). Vamos voltar a gravar regra de actualização gradiente de descida, mudança de variáveis v _j pesos e deslocamentos. Em outras palavras, agora nossa “posição” possui os componentes w _k e b _l , e o vetor gradiente ∇C tem os componentes correspondentes ∂C / ∂w_k e ∂C / ∂b _l . Depois de escrever nossa regra de atualização com novos componentes, obtemos:

$$

$$w_k \rightarrow w'_k = w_k - \eta \frac{\partial C}{\partial w_k} \tag{16}$$

$$

$$b_l \rightarrow b'_l = b_l - \eta \frac{\partial C}{\partial b_l} \tag{17}$$

Ao reaplicar esta regra de atualização, podemos "rolar ladeira abaixo" e, com alguma sorte, encontrar a função de custo mínimo. Em outras palavras, essa regra pode ser usada para treinar a Assembléia Nacional.

Existem vários obstáculos para aplicar a regra de descida do gradiente. Nós os estudaremos em mais detalhes nos próximos capítulos. Mas, por enquanto, quero mencionar apenas um problema. Para entendê-lo, voltemos ao valor quadrático na equação (6). Observe que essa função de custo se parece com C = 1 / n C _x C _x , ou seja, é o custo médio C _x ≡ (|| y (x) −a || ² ) / 2 para exemplos de treinamento individuais. Na prática, para calcular o gradiente ∇C, precisamos calcular os gradientes ∇C _x separadamente para cada entrada de treinamento x e depois calculá-los como média, averageC = 1 / n ∑ _x ∇C _x . Infelizmente, quando a quantidade de entrada for muito grande, levará muito tempo e esse treinamento será lento.

Para acelerar o aprendizado, você pode usar a descida estocástica do gradiente. A idéia é calcular aproximadamente o gradiente de byC calculando ∇C _x para uma pequena amostra aleatória de entrada de treinamento. Ao calcular sua média, podemos obter rapidamente uma boa estimativa do gradiente verdadeiro ∇C, e isso ajuda a acelerar a descida do gradiente e, portanto, o treinamento.

Formulando com mais precisão, a descida do gradiente estocástico funciona através da amostragem aleatória de um pequeno número de m dados de entrada de treinamento. Nós chamaremos esses dados aleatórios de X ₁ , X ₂ , .., X me chamaremos de minipacote. Se o tamanho da amostra m for grande o suficiente, o valor médio de ∇C _{X j} será próximo o suficiente da média de todos os ∇Cx, ou seja,

$$

$$\ frac {\ sum ^ m_ {j = 1} \ nabla C_ {X_j}} {m} \ approx \ frac {\ sum_x \ nabla C_x} {n} = \ nabla C \ tag {18}$$

onde o segundo valor passa por todo o conjunto de dados de treinamento. Ao trocar peças, obtemos

$$

$$\ nabla C \ approx \ frac {1} {m} \ sum ^ m_ {j = 1} \ nabla C_ {X_j} \ tag {19}$$

o que confirma que podemos estimar o gradiente geral calculando os gradientes para um minipack selecionado aleatoriamente.

Para relacionar isso diretamente ao treinamento de NS, vamos supor que w _k e b _l denotem os pesos e deslocamentos de nosso NS. Em seguida, a descida do gradiente estocástico seleciona um mini-pacote aleatório de dados de entrada e aprende com eles

$$

$$w_k \ rightarrow w'_k = w_k - \ frac {\ eta} {m} \ sum_j \ frac {\ C_ parcial {X_j}} {\ w_k parcial} \ tag {20}$$

$$

$$b_l \ rightarrow b'_l = b_l - \ frac {\ eta} {m} \ sum_j \ frac {\ C_ parcial {X_j}} {\ b_l parcial} \ tag {21}$$

onde está a soma de todos os exemplos de treinamento X _j no _minipacote atual. Depois, selecionamos outro mini-pacote aleatório e estudamos sobre ele. E assim por diante, até esgotarmos todos os dados de treinamento, chamados de fim da era do treinamento. Neste momento, estamos iniciando novamente uma nova era de aprendizado.

A propósito, vale a pena notar que os acordos referentes à escala da função de custo e à atualização dos pesos e compensações diferem em um minipacote. Na equação (6), escalamos a função de custo 1 / n vezes. Às vezes, as pessoas omitem 1 / n somando os custos de exemplos de treinamento individuais, em vez de calcular a média. Isso é útil quando o número total de exemplos de treinamento não é conhecido antecipadamente. Isso pode acontecer, por exemplo, quando dados adicionais aparecerem em tempo real. Da mesma forma, as regras de atualização do mini-pacote (20) e (21) às vezes omitem o membro de 1 / m na frente da soma. Conceitualmente, isso não afeta nada, pois é equivalente a uma mudança na velocidade de aprendizado η. No entanto, vale a pena prestar atenção ao comparar vários trabalhos.

Uma descida estocástica de gradiente pode ser vista como um voto político: é muito mais fácil coletar uma amostra na forma de um minipacote do que aplicar uma descida de gradiente a uma amostra completa - assim como uma pesquisa na saída de um site é mais fácil de realizar do que uma eleição completa. Por exemplo, se o nosso conjunto de treinamento tiver um tamanho de n = 60.000, como o MNIST, e fizermos uma amostra de um mini-pacote de tamanho m = 10, aceleraremos a estimativa do gradiente em 6000 vezes! Obviamente, a estimativa não será ideal - haverá flutuação estatística nela - mas não precisará ser ideal: precisamos apenas avançar na direção que diminui C, o que significa que não precisamos calcular o gradiente com precisão. Na prática, a descida estocástica do gradiente é uma técnica de ensino comum e poderosa para a Assembléia Nacional, e a base da maioria das tecnologias de ensino que iremos desenvolver como parte do livro.

Exercícios

• A versão extrema da descida em gradiente usa o tamanho de minipacote igual a 1. Ou seja, com a entrada x, atualizamos nossos pesos e compensações de acordo com as regras w _k → w ′ _k = w _k - η /C _x / ∂w _k eb b _l → b ′ _L = b _l - ηC _x / ∂b _l . Em seguida, selecionamos outro exemplo de entrada de treinamento e atualizamos novamente os pesos e compensações. E assim por diante Este procedimento é conhecido como aprendizado online ou incremental. No aprendizado on-line, o NS estuda com base em uma cópia de treinamento dos dados de entrada de cada vez (como pessoas). Quais são as vantagens e desvantagens do aprendizado on-line em comparação com a descida gradiente estocástica com um tamanho de minipacote de 20?

Deixe-me terminar esta seção com uma discussão sobre um tópico que às vezes incomoda as pessoas que encontraram pela primeira vez uma descida de gradiente. No NS, o valor de C é uma função de muitas variáveis ​​- todos os pesos e compensações - e, em certo sentido, determina a superfície em um espaço muito multidimensional. As pessoas começam a pensar: "Vou ter que visualizar todas essas dimensões adicionais". E eles começam a se preocupar: "Não consigo navegar em quatro dimensões, sem mencionar cinco (ou cinco milhões)". Eles têm alguma qualidade especial que a supermatemática "real" tem? Claro que não. Até matemáticos profissionais não conseguem visualizar muito bem o espaço quadridimensional - se é que o fazem. Eles fazem truques, desenvolvendo outras maneiras de representar o que está acontecendo. Fizemos exatamente isso: usamos a representação algébrica (e não visual) de ΔC para entender como se mover para que C diminua. Pessoas que fazem um bom trabalho com um grande número de dimensões têm em mente uma grande biblioteca de técnicas semelhantes; nosso truque algébrico é apenas um exemplo. Essas técnicas podem não ser tão simples como estamos acostumados ao visualizar três dimensões, mas quando você cria uma biblioteca de técnicas semelhantes, começa a pensar bem em dimensões superiores. Não entrarei em detalhes, mas se você estiver interessado, talvez goste da discussão de algumas dessas técnicas por matemáticos profissionais que estão acostumados a pensar em dimensões mais elevadas. Embora algumas das técnicas discutidas sejam bastante complexas, a maioria das melhores respostas é intuitiva e acessível a todos.

Implementando uma Rede para Classificar Números

Ok, agora vamos escrever um programa que aprenda a reconhecer dígitos manuscritos usando descida estocástica de gradiente e dados de treinamento do MNIST. Faremos isso com um pequeno programa em python 2.7, composto por apenas 74 linhas! A primeira coisa que precisamos é fazer o download dos dados do MNIST. Se você usa git, pode obtê-los clonando o repositório deste livro:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git

Caso contrário, faça o download do código no link .

A propósito, quando mencionei os dados do MNIST anteriormente, eu disse que eles são divididos em 60.000 imagens de treinamento e 10.000 imagens de teste. Esta é a descrição oficial do MNIST. Vamos quebrar os dados um pouco diferente. Deixaremos as imagens de verificação inalteradas, mas dividiremos o conjunto de treinamento em duas partes: 50.000 imagens, que usaremos para treinar a Assembléia Nacional, e 10.000 imagens individuais para confirmação adicional. Embora não os utilizemos, mais tarde eles serão úteis quando entenderemos a configuração de alguns hiper parâmetros do NS - a velocidade de aprendizado etc. - que nosso algoritmo não seleciona diretamente. Embora os dados de corroboração não façam parte da especificação original do MNIST, muitos usam o MNIST dessa maneira e, no campo do HC, o uso de dados de corroboração é comum. Agora, falando dos "dados de treinamento do MNIST", quero dizer nossos 50.000 karitnoks, não os 60.000 originais.

Além dos dados MNIST, também precisamos de uma biblioteca python chamada Numpy para cálculos rápidos de álgebra linear. Se você não o possui, pode obtê-lo no link .

Antes de fornecer todo o programa, deixe-me explicar os principais recursos do código para o NS. O local central é ocupado pela classe Rede, que usamos para representar a Assembléia Nacional. Aqui está o código de inicialização do objeto Rede:

 class Network(object): def __init__(self, sizes): self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] 

A matriz de tamanhos contém o número de neurônios nas camadas correspondentes. Portanto, se queremos criar um objeto de rede com dois neurônios na primeira camada, três neurônios na segunda camada e um neurônio na terceira, então o escreveremos assim:

 net = Network([2, 3, 1]) 

As compensações e pesos no objeto Rede são inicializados aleatoriamente usando a função numpy np.random.randn, que gera uma distribuição Gaussiana com uma expectativa matemática de 0 e um desvio padrão de 1. Essa inicialização aleatória fornece um ponto de partida ao nosso algoritmo de descida de gradiente estocástico. Nos capítulos seguintes, encontraremos as melhores maneiras de inicializar pesos e compensações, mas por enquanto isso é suficiente. Observe que o código de inicialização de rede pressupõe que a primeira camada de neurônios será inserida e não lhes atribui um viés, pois eles são usados ​​apenas para calcular a saída.

Observe também que deslocamentos e pesos são armazenados como uma matriz de matrizes Numpy. Por exemplo, net.weights [1] é uma matriz Numpy que armazena pesos que conectam a segunda e a terceira camadas de neurônios (essa não é a primeira e a segunda camadas, pois em python a numeração dos elementos da matriz vem do zero). Como levará muito tempo para escrever net.weights [1], denotamos essa matriz como w. Essa é uma matriz que w _jk é o peso da conexão entre o k-ésimo neurônio na segunda camada e o j-ésimo neurônio na terceira. Essa ordem de índices j e k pode parecer estranha - não seria mais lógico trocá-los? Mas a grande vantagem desse registro será que o vetor de ativação da terceira camada de neurônios é obtido:

$$

$$a '= \ sigma (wa + b) \ tag {22}$$

Vamos olhar para esta equação bastante rica. a é o vetor de ativação da segunda camada de neurônios. Para obter a ', multiplicamos a pela matriz de pesos w e adicionamos o vetor de deslocamento b. Em seguida, aplicamos o elemento sigmóide σ por elemento a cada elemento do vetor wa + b (isso é chamado de vetorização da função σ). É fácil verificar que a equação (22) fornece o mesmo resultado que a regra (4) para calcular um neurônio sigmóide.

Exercício

• Escreva a equação (22) na forma de componente e verifique se ela fornece o mesmo resultado da regra (4) para calcular um neurônio sigmóide.

Com tudo isso em mente, é fácil escrever código que calcula a saída de um objeto de rede. Começamos definindo um sigmóide:

 def sigmoid(z): return 1.0/(1.0+np.exp(-z)) 

Observe que, quando o parâmetro z for um vetor ou matriz Numpy, o Numpy aplicará automaticamente o elemento sigmóide, ou seja, na forma de vetor.

Adicione um método de propagação direta à classe Network, que recebe a entrada a da rede e retorna a saída correspondente. Supõe-se que o parâmetro a seja (n, 1) Numpy ndarray, não um vetor (n,). Aqui n é o número de neurônios de entrada. Se você tentar usar o vetor (n), obterá resultados estranhos.

O método simplesmente aplica a equação (22) a cada camada:

  def feedforward(self, a): """       "a"""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a 

Claro, basicamente nós, dos objetos de Rede, precisamos deles para aprender. Para isso, forneceremos a eles o método SGD, que implementa a descida estocástica do gradiente. Aqui está o código dele. Em alguns lugares, é bastante misterioso, mas a seguir iremos analisá-lo em mais detalhes.

  def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) 

training_data é uma lista de tuplas "(x, y)" que representam a entrada de treinamento e a saída desejada. As variáveis ​​epochs e mini_batch_size são o número de épocas a serem aprendidas e o tamanho dos minipacotes a serem usados. eta - velocidade de aprendizagem, η. Se test_data estiver definido, a rede será avaliada com relação aos dados de verificação após cada era e o progresso atual será exibido. Isso é útil para acompanhar o progresso, mas diminui significativamente o trabalho.

O código funciona assim. Em cada época, ele começa misturando acidentalmente os dados de treinamento e os divide em mini-pacotes do tamanho certo. Essa é uma maneira fácil de criar uma amostra de dados de treinamento. Em seguida, para cada mini_batch, aplicamos uma etapa de descida de gradiente. Isso é feito pelo código self.update_mini_batch (mini_batch, eta), que atualiza os pesos e compensações da rede de acordo com uma iteração de descida de gradiente único usando apenas dados de treinamento no mini_batch. Aqui está o código para o método update_mini_batch:

  def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] 

A maior parte do trabalho é feita pela linha.

  delta_nabla_b, delta_nabla_w = self.backprop(x, y) 

Invoca um algoritmo de retropropagação - uma maneira rápida de calcular o gradiente de uma função de custo. Portanto, update_mini_batch simplesmente calcula esses gradientes para cada exemplo de treinamento de mini_batch e atualiza self.weights e self.biases.

Até agora, não demonstrarei código para self.backprop. O trabalho de distribuição reversa será explorado no próximo capítulo, e haverá um código self.backprop. Por enquanto, suponha que ele se comporte como indicado, retornando um gradiente apropriado para o custo associado ao exemplo de treinamento x.

Vamos dar uma olhada em todo o programa, incluindo comentários explicativos. Com exceção da função self.backprop, o programa fala por si - o trabalho principal é realizado por self.SGD e self.update_mini_batch. O método self.backprop usa várias funções adicionais para calcular o gradiente, ou seja, sigmoid_prime, que calcula a derivada do sigmoide, e self.cost_derivative, que não descreverei aqui. Você pode ter uma idéia deles observando o código e os comentários. No próximo capítulo, vamos considerá-los com mais detalhes. Lembre-se de que, embora o programa pareça longo, a maior parte do código são comentários que facilitam o entendimento. De fato, o próprio programa consiste em apenas 74 linhas não de código - não vazias e nem comentários. Todo o código está disponível no GitHub .

 """ network.py ~~~~~~~~~~           .      .     ,    .   ,       . """ ####  #   import random #   import numpy as np class Network(object): def __init__(self, sizes): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].               0    1. ,      ,       ,        . """ self.num_layers = len(sizes) self.sizes = sizes self.biases = [np.random.randn(y, 1) for y in sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])] def feedforward(self, a): """   ,  ``a`` -  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None): """    -    . training_data –   "(x, y)",       .       .  test_data ,          ,     .     ,    . """ if test_data: n_test = len(test_data) n = len(training_data) for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch(mini_batch, eta) if test_data: print "Epoch {0}: {1} / {2}".format( j, self.evaluate(test_data), n_test) else: print "Epoch {0} complete".format(j) def update_mini_batch(self, mini_batch, eta): """    ,          -. mini_batch –    (x, y),  eta –  .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) #   delta = self.cost_derivative(activations[-1], y) * \ sigmoid_prime(zs[-1]) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """ l      ,      . l = 1    , l = 2 – ,   .    ,   python      .""" for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def evaluate(self, test_data): """    ,      .    –          .""" test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data] return sum(int(x == y) for (x, y) in test_results) def cost_derivative(self, output_activations, y): """    ( C_x /  a)   .""" return (output_activations-y) ####   def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

Quão bem o programa reconhece números manuscritos? Vamos começar carregando os dados do MNIST. Faremos isso usando o pequeno programa auxiliar mnist_loader.py, que descreverei abaixo. Execute os seguintes comandos no shell python:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Obviamente, isso pode ser feito em um programa separado, mas se você trabalhar em paralelo com um livro, será mais fácil.

Depois de baixar os dados do MNIST, configure uma rede de 30 neurônios ocultos. Faremos isso depois de importar o programa descrito acima, chamado de rede:

 >>> import network >>> net = network.Network([784, 30, 10]) 

Finalmente, usamos descida de gradiente estocástico para treinamento em dados de treinamento por 30 eras, com tamanho de minipacote de 10 e velocidade de aprendizado de η = 3,0:

 >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Se você estiver executando um código paralelamente à leitura de um livro, lembre-se de que levará alguns minutos para executar. Sugiro que você comece tudo, continue lendo e verifique periodicamente o que o programa produz. Se você estiver com pressa, poderá reduzir o número de eras, reduzindo o número de neurônios ocultos ou usando apenas parte dos dados de treinamento. O código de trabalho final funcionará mais rápido: esses scripts python foram projetados para fazer você entender como a rede funciona e não possui alto desempenho! E, é claro, após o treinamento, a rede pode funcionar muito rapidamente em praticamente qualquer plataforma de computação. Por exemplo, quando ensinamos à rede uma boa seleção de pesos e compensações, ela pode ser transportada facilmente para trabalhar em JavaScript em um navegador da Web ou como um aplicativo nativo em um dispositivo móvel. De qualquer forma, aproximadamente a mesma conclusão é feita pelo programa que treina a rede neural. Ela escreve o número de imagens de teste reconhecidas corretamente após cada era de treinamento. Como você pode ver, mesmo após uma era, atinge uma precisão de 9.129 em 10.000, e esse número continua a crescer:

Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000

Acontece que a rede treinada fornece uma porcentagem da classificação correta de cerca de 95 - 95,42% no máximo! Uma primeira tentativa bastante promissora. Eu aviso que seu código não necessariamente produzirá exatamente os mesmos resultados, pois inicializamos a rede com pesos e compensações aleatórios. Para este capítulo, eu escolhi a melhor de três tentativas.

Vamos reiniciar o experimento alterando o número de neurônios ocultos para 100. Como antes, se você executar o código ao mesmo tempo que lê, lembre-se de que leva muito tempo (na minha máquina, cada época leva várias dezenas de segundos), então é melhor ler em paralelo com execução de código.

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data) 

Naturalmente, isso melhora o resultado para 96,59%. Pelo menos nesse caso, o uso de mais neurônios ocultos ajuda a obter melhores resultados.

O feedback dos leitores sugere que os resultados deste experimento variam muito e alguns resultados de aprendizado são muito piores. Usando técnicas do Capítulo 3 para reduzir seriamente a diversidade da eficiência do trabalho de uma execução para outra.

Obviamente, para alcançar tal precisão, eu tive que escolher um certo número de épocas para aprender, o tamanho do mini-pacote e a velocidade de aprendizado η. Como mencionei acima, eles são chamados hiperparâmetros de nossa Assembléia Nacional - para distingui-los de parâmetros simples (pesos e compensações) que o algoritmo ajusta durante o treinamento. Se escolhermos mal os hiperparâmetros, obteremos resultados ruins. Suponha, por exemplo, que tenhamos escolhido a taxa de aprendizado η = 0,001:

 >>> net = network.Network([784, 100, 10]) >>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data) 

Os resultados são muito menos impressionantes:

Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000

No entanto, você pode ver que a eficiência da rede está crescendo lentamente ao longo do tempo. Isso sugere que você pode tentar aumentar a velocidade de aprendizado, por exemplo, para 0,01. Nesse caso, os resultados serão melhores, o que indica a necessidade de aumentar ainda mais a velocidade (se a mudança melhorar a situação, mude ainda mais!). Se você fizer isso várias vezes, chegaremos a η = 1,0 (e às vezes até 3,0), o que está próximo de nossas experiências anteriores. Portanto, embora inicialmente tenhamos selecionado mal parâmetros hiperparâmetro, pelo menos reunimos informações suficientes para melhorar nossa escolha de parâmetros.

Em geral, a depuração de NA é uma questão complicada. Isso ocorre especialmente quando a escolha dos hiperparâmetros iniciais produz resultados que não excedem o ruído aleatório. Suponha que tentemos usar uma arquitetura bem-sucedida de 30 neurônios, mas alteremos a velocidade de aprendizado para 100.0:

 >>> net = network.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data) 

No final, acontece que fomos longe demais e pegamos muita velocidade:

Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000

Agora imagine que estamos abordando essa tarefa pela primeira vez. Obviamente, sabemos desde os primeiros experimentos que seria correto reduzir a velocidade do aprendizado. Mas se abordássemos essa tarefa pela primeira vez, não teríamos resultados que pudessem nos levar à solução certa. Poderíamos começar a pensar que talvez tenhamos escolhido os parâmetros iniciais errados para pesos e compensações, e é difícil para a rede aprender? Ou talvez não tenhamos dados de treinamento suficientes para obter um resultado significativo? Talvez não tenhamos esperado épocas suficientes? Talvez uma rede neural com essa arquitetura simplesmente não consiga aprender a reconhecer números manuscritos? Talvez a velocidade de aprendizado seja muito lenta? Quando você aborda a tarefa pela primeira vez, nunca tem confiança.

Com isso, vale a pena aprender uma lição de que depurar o NS não é uma tarefa trivial e isso, como a programação regular, faz parte da arte. Você deve aprender esta arte de depuração para obter bons resultados do NS. Em geral, precisamos desenvolver uma heurística para selecionar bons hiperparâmetros e boa arquitetura. Discutiremos isso em detalhes no livro, incluindo como selecionei os hiperparâmetros acima.

Exercício

• Tente criar uma rede de apenas duas camadas - entrada e saída, sem ocultar - com 784 e 10 neurônios, respectivamente.Treine a rede com descida de gradiente estocástico. Que precisão de classificação você obtém?

Anteriormente, pulei os detalhes do carregamento de dados MNIST. Isso acontece simplesmente. Aqui está o código para completar a imagem. As estruturas de dados são descritas nos comentários - tudo é simples, tuplas e matrizes de objetos Numpy ndarray (se você não estiver familiarizado com esses objetos, pense neles como vetores).

 """ mnist_loader ~~~~~~~~~~~~      MNIST.       ``load_data``  ``load_data_wrapper``.  , ``load_data_wrapper`` -  ,     . """ ####  #  import cPickle import gzip #  import numpy as np def load_data(): """  MNIST   ,  ,    . ``training_data``      .    .  numpy ndarray  50 000 .   –     numpy ndarray  784 ,  28 * 28 = 784    MNIST.  –  numpy ndarray  50 000 .   –   0  9   ,    . ``validation_data``  ``test_data`` ,    10 000 .    ,           ``training_data``.    - ``load_data_wrapper()``. """ f = gzip.open('../data/mnist.pkl.gz', 'rb') training_data, validation_data, test_data = cPickle.load(f) f.close() return (training_data, validation_data, test_data) def load_data_wrapper(): """ ,  ``(training_data, validation_data, test_data)``.   ``load_data``,         .  , ``training_data`` -    50 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   . ``y`` -  10- numpy.ndarray,   ,     ``x``. ``validation_data``  ``test_data`` -  ,   10 000    , ``(x, y)``. ``x`` -  784- numpy.ndarray,   ,  ``y`` -   ,  ,   ( ),  ``x``. ,  ,           .         .""" tr_d, va_d, te_d = load_data() training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]] training_results = [vectorized_result(y) for y in tr_d[1]] training_data = zip(training_inputs, training_results) validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]] validation_data = zip(validation_inputs, va_d[1]) test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]] test_data = zip(test_inputs, te_d[1]) return (training_data, validation_data, test_data) def vectorized_result(j): """ 10-    1.0   j     .      (0..9)     .""" e = np.zeros((10, 1)) e[j] = 1.0 return e 

Eu disse que nosso programa está obtendo bons resultados. O que isso significa? Bom em comparação com o que? É útil obter os resultados de alguns testes simples e básicos com os quais você pode fazer uma comparação para entender o que “bons resultados” significam. O nível básico mais simples, é claro, seria um palpite aleatório. Isso pode ser feito em cerca de 10% dos casos. E nós mostramos um resultado muito melhor!

Que tal um nível base menos trivial? Vamos ver como a imagem está escura. Por exemplo, a imagem 2 geralmente será mais escura que a imagem 1, simplesmente porque possui mais pixels escuros, como visto nos exemplos abaixo:



Conclui-se que podemos calcular a escuridão média para cada dígito de 0 a 9. Quando obtemos uma nova imagem, calculamos sua escuridão e achamos que ela mostra uma figura com a escuridão média mais próxima. Este é um procedimento simples e fácil de programar, por isso não escreverei código - se estiver interessado, ele fica no GitHub . Mas essa é uma melhoria séria em comparação com suposições aleatórias - o código reconhece corretamente 2.225 de 10.000 imagens, ou seja, fornece uma precisão de 22,25%.

Não é difícil encontrar outras idéias que atinjam precisão entre 20 e 50%. Depois de trabalhar um pouco mais, você pode exceder 50%. Mas, para obter uma precisão muito maior, é melhor usar algoritmos MO autorizados. Vamos tentar um dos algoritmos mais famosos, o método do vetor de suporte ou SVM. Se você não conhece o SVM, não se preocupe, não precisamos entender esses detalhes. Apenas usamos uma biblioteca python chamada scikit-learn, que fornece uma interface simples para a biblioteca C rápida para SVM, conhecida como LIBSVM .

Se executarmos o scikit-learn do classificador SVM nas configurações padrão, obteremos a classificação correta de 9.435 em 10.000 (o código está disponível no link) Isso já é uma grande melhoria em relação à abordagem ingênua de classificar imagens pela escuridão. Isso significa que o SVM funciona tão bem quanto o nosso NS, apenas um pouco pior. Nos capítulos seguintes, vamos nos familiarizar com novas técnicas que nos permitirão melhorar nosso NS para que eles superem em muito o SVM.

Mas isso não é tudo.O resultado 9 435 em 10 000 do scikit-learn é especificado para as configurações padrão. O SVM possui muitos parâmetros que podem ser ajustados e você pode procurar parâmetros que melhorem esse resultado. Não vou entrar em detalhes, eles podem ser lidos no artigo de Andreas Muller. Ele mostrou que, trabalhando para otimizar os parâmetros, é possível obter uma precisão de pelo menos 98,5%. Em outras palavras, um SVM bem ajustado comete apenas um dígito dentre os 70 erros. Um bom resultado! NA pode conseguir mais?

Acontece que eles podem. Hoje, um NS bem ajustado ultrapassa qualquer outra tecnologia conhecida na solução MNIST, incluindo o SVM. Registro para 2013classificou corretamente 9.979 de 10.000 imagens. E veremos a maioria das tecnologias usadas para isso neste livro. Esse nível de precisão é próximo ao humano, e talvez até o exceda, pois várias imagens do MNIST são difíceis de decifrar, mesmo para humanos, por exemplo: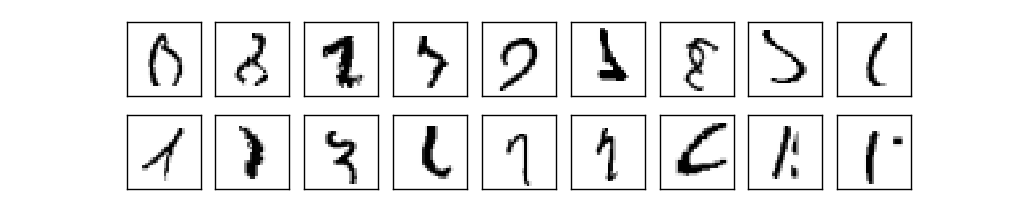



acho que você concorda que é difícil classificá-las! Com essas imagens no conjunto de dados MNIST, é surpreendente que o NS possa reconhecer corretamente todas as 10.000 imagens, exceto 21. Geralmente, os programadores acreditam que resolver uma tarefa tão complexa exige um algoritmo complexo. Mas até o NS está trabalhandoo detentor do registro usa algoritmos bastante simples, que são pequenas variações daqueles que examinamos neste capítulo. Toda a complexidade aparece automaticamente durante o treinamento com base em dados de treinamento. Em certo sentido, a moral de nossos resultados e os contidos em trabalhos mais complexos é que, para algumas tarefas

algoritmo complexo ≤ algoritmo de treinamento simples + bons dados de treinamento

Para aprendizagem profunda

Embora nossa rede esteja mostrando um desempenho impressionante, ela é alcançada de maneira misteriosa. Pesos e redes de mistura são detectados automaticamente. Portanto, não temos uma explicação pronta de como a rede faz o que faz. Existe alguma maneira de entender os princípios básicos de classificação por uma rede de números manuscritos? E é possível, dados a eles, melhorar o resultado?

Reformulamos essas questões de maneira mais rigorosa: suponhamos que em algumas décadas o SN se transforme em inteligência artificial (IA). Vamos entender como essa IA funciona? Talvez as redes permaneçam incompreensíveis para nós, com seus pesos e compensações, uma vez que são atribuídas automaticamente. Nos primeiros anos da pesquisa em IA, as pessoas esperavam que tentar criar IA também nos ajudasse a entender os princípios subjacentes à inteligência, e talvez até o trabalho do cérebro humano. No entanto, no final, pode acontecer que não entendamos nem o cérebro nem como a IA funciona!

Para lidar com essas questões, lembremos da interpretação dos neurônios artificiais que dei no começo do capítulo - que essa é uma maneira de pesar evidências. Suponha que desejamos determinar se o rosto de uma pessoa está em uma imagem:







Esse problema pode ser abordado da mesma maneira que o reconhecimento de escrita: usando pixels de imagem como entrada para o NS, e a saída do NS será um neurônio que dirá: "Sim, isso é um rosto" ou "Não, isso não é um rosto. "

Suponha que façamos isso, mas sem usar um algoritmo de aprendizado. Vamos tentar criar manualmente uma rede, escolhendo os pesos e compensações apropriados. Como podemos abordar isso? Por um momento, esquecendo a Assembléia Nacional, poderíamos dividir a tarefa em subtarefas: a imagem dos olhos tem no canto superior esquerdo? Existe um olho no canto superior direito? Existe um nariz do meio? Existe uma boca no meio? Existe cabelo no topo? E assim por diante

Se as respostas para várias dessas perguntas forem positivas, ou mesmo "provavelmente sim", concluímos que a imagem pode ter um rosto. Por outro lado, se as respostas forem não, provavelmente não há pessoa.

É claro que essa é uma heurística aproximada e possui muitas deficiências. Talvez este seja um homem careca, e ele não tem cabelo. Talvez possamos ver apenas parte do rosto, ou o rosto em ângulo, de modo que algumas partes do rosto estejam fechadas. No entanto, a heurística sugere que, se pudermos resolver subproblemas com a ajuda de redes neurais, talvez possamos criar NSs para reconhecimento de face combinando redes para subtarefas. A seguir, é apresentada uma arquitetura possível de uma rede na qual as sub-redes são indicadas por retângulos. Essa não é uma abordagem completamente realista para solucionar o problema de reconhecimento de face: é necessária para nos ajudar a entender intuitivamente o trabalho das redes neurais.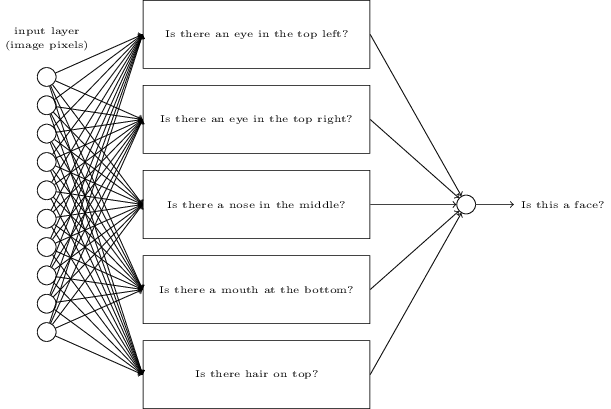


Nos retângulos existem subtarefas: a imagem dos olhos tem no canto superior esquerdo? Existe um olho no canto superior direito? Existe um nariz do meio? Existe uma boca no meio? Existe cabelo no topo? E assim por diante

É possível que as sub-redes também possam ser desmontadas em componentes. Pegue a questão de ter um olho no canto superior esquerdo. Pode ser distinguido em perguntas como: "Existe uma sobrancelha?", "Existem cílios?", "Existe um aluno?" e assim por diante. Obviamente, as perguntas devem conter informações sobre o local - "A sobrancelha está localizada no canto superior esquerdo, acima da pupila?", E assim por diante - mas vamos simplificá-lo por enquanto. Portanto, a rede que responde à pergunta sobre a presença do olho pode ser desmontada nos componentes:


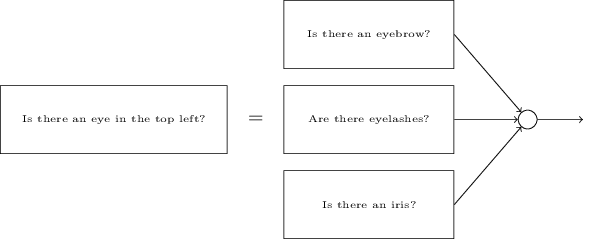“Existe uma sobrancelha?”, “Existem cílios?”, “Existe uma pupila?”

Essas perguntas podem ser divididas em pequenas, em etapas através de várias camadas. Como resultado, trabalharemos com sub-redes que respondem a perguntas tão simples que podem ser facilmente desmontadas no nível de pixel. Essas perguntas podem dizer respeito, por exemplo, à presença ou ausência de formas simples em determinados locais da imagem. Neurônios individuais associados a pixels poderão responder a eles.

O resultado é uma rede que divide perguntas muito complexas - se uma pessoa está na imagem - em perguntas muito simples que podem ser respondidas no nível de pixel individual. Ela fará isso através de uma sequência de várias camadas, nas quais as primeiras respondem a perguntas muito simples e específicas sobre a imagem, e as últimas criam uma hierarquia de conceitos mais complexos e abstratos. As redes com uma estrutura multicamada - duas ou mais camadas ocultas - são chamadas de redes neurais profundas (GNS).

Claro, eu não falei sobre como fazer essa sub-rede recursiva. Definitivamente, será impraticável selecionar manualmente pesos e compensações. Gostaríamos de usar algoritmos de treinamento para que a rede aprenda automaticamente pesos e desvios - e através deles as hierarquias de conceitos - com base nos dados de treinamento. Pesquisadores nas décadas de 1980 e 1990 tentaram usar a descida do gradiente estocástico e a retropropagação para treinar o GNS. Infelizmente, com exceção de algumas arquiteturas especiais, elas não tiveram êxito. As redes treinaram, mas muito lentamente, e, na prática, era muito lento para ser usado de alguma maneira.

Desde 2006, várias tecnologias foram desenvolvidas para treinar STS. Eles são baseados na descida do gradiente estocástico e na propagação de retorno, mas também contêm novas idéias. Eles permitiram treinar redes muito mais profundas - hoje as pessoas treinam silenciosamente redes com 5 a 10 camadas. E acontece que eles resolvem muitos problemas muito melhor do que os NSs rasos, ou seja, redes com uma camada oculta. A razão, é claro, é que o STS pode criar uma hierarquia complexa de conceitos. É semelhante à maneira como as linguagens de programação usam esquemas modulares e idéias de abstração para que possam criar programas de computador complexos. Comparar um NS profundo com um NS raso é aproximadamente como comparar uma linguagem de programação que pode fazer chamadas de função com uma linguagem que não. A abstração no NS não se parece com linguagens de programação,mas tem a mesma importância.