Que haja algum experimento abstrato no processo em que um determinado evento possa ocorrer. Esse experimento foi realizado cinco vezes e em quatro deles ocorreu o mesmo evento. Que conclusões podem ser tiradas destes 4/5?

Existe
uma fórmula de Bernoulli que fornece a resposta com qual probabilidade 4 de 5 ocorre com uma probabilidade inicial conhecida. Mas ela não responde, qual era a probabilidade inicial se os eventos fossem 4 em 5. Vamos deixar de lado a fórmula de Bernoulli.
Vamos fazer um pequeno programa simples que simule os processos de probabilidade para esse caso e, com base no resultado dos cálculos, construímos um gráfico.
void test1() { uint sz_ar_events = 50;
O código para este programa pode ser encontrado
aqui , junto com as funções auxiliares.
O cálculo foi lançado no Excel e fez um cronograma.

Essa versão do gráfico pode ser chamada de distribuição de densidade de probabilidade do valor de probabilidade. Sua área é igual à unidade que é distribuída neste monte.
Para concluir a imagem, mencionarei que este gráfico corresponde ao gráfico de acordo com a fórmula de Bernoulli do parâmetro de probabilidade e multiplicado por N + 1 o número de experimentos.
Além disso, no texto, onde uso uma fração da forma k / n no artigo, essa não é uma divisão, são k eventos de n experimentos, para não escrever k de n todas as vezes.
Próximo. É possível aumentar o número de experimentos e obter uma região mais estreita da localização dos principais valores do valor de probabilidade, mas não importa como eles sejam aumentados, essa região não será reduzida para a região zero com uma probabilidade conhecida.
O gráfico abaixo mostra as distribuições para 4/5, 7/9, 11/14 e 24/30. Quanto mais estreita a área, maior o monte, cuja área é uma unidade constante. Essas relações foram escolhidas porque são todas de cerca de 0,8, e não porque são exatamente essas que podem surgir a 0,8 da probabilidade inicial. Selecionado para demonstrar qual faixa de valores possíveis permanece, mesmo com 30 experimentos realizados.
O código do programa para este gráfico está
aqui .

Disso se segue que, na realidade, a probabilidade experimental não pode ser exatamente determinada, mas podemos apenas assumir a região da possível localização de tal quantidade, com precisão, dependendo de quantas medidas foram tomadas.
Não importa quantas experiências sejam realizadas, sempre existe a possibilidade de a probabilidade inicial ser de 0,0001 e 0,9999. Por simplicidade, valores improváveis extremos são descartados. E tomamos, por exemplo, 95% da área principal do cronograma de distribuição.
Tal coisa é chamada de intervalos de confiança. Não cumpri nenhuma recomendação sobre quanto e por que os juros devem ser deixados. Para a previsão do tempo, leve menos, para lançar mais ônibus espaciais. Eles também geralmente não mencionam qual intervalo de confiança é utilizado para a probabilidade de eventos e se é usado.
No meu programa, o cálculo dos limites do intervalo de confiança é realizado
aqui .
Verificou-se que a probabilidade do evento é determinada pela densidade de probabilidade do valor da probabilidade, e ainda é necessário impor uma porcentagem da área dos valores principais para que você possa pelo menos dizer com certeza que tipo de probabilidade é o evento em estudo.
Agora, sobre um experimento mais real.
Deixe todo mundo ficar entediado com uma moeda, jogue essa moeda e receba 4 de 5 gotas por coroa - um caso muito real. De fato, isso não é exatamente o mesmo que o descrito um pouco mais alto. Como isso é diferente do experimento anterior?
O experimento anterior foi descrito no pressuposto de que a probabilidade do evento pode ser igualmente distribuída no intervalo de 0 a 1. No programa, isso é especificado pela linha
probabilidade dupla = get_random_real_0_1 (); . Mas não há moedas com probabilidade de cair, digamos, 0,1 ou 0,9 estão sempre de um lado.
Se você pegar mil moedas diferentes do comum ao mais curvado, e para cada uma medir a perda jogando-a mil ou mais vezes, isso mostrará que elas realmente caem de um lado no intervalo de 0,4 a 0,6 (estes são números aleatórios, não vou mas procuro 1000 moedas e jogo a cada 1000 vezes).
Como esse fato altera o programa de simulação das probabilidades de uma moeda em particular, para a qual foram recebidas 4 de 5 caudas?
Suponha que a distribuição da perda de um lado para moedas seja descrita como uma aproximação ao gráfico da distribuição normal obtida com os parâmetros média = 0,5, desvio padrão = 0,1. (no gráfico abaixo, é mostrado em preto).
Quando em um programa altero a geração da probabilidade inicial de igualmente distribuída para distribuída de acordo com a regra especificada, obtenho os seguintes gráficos:
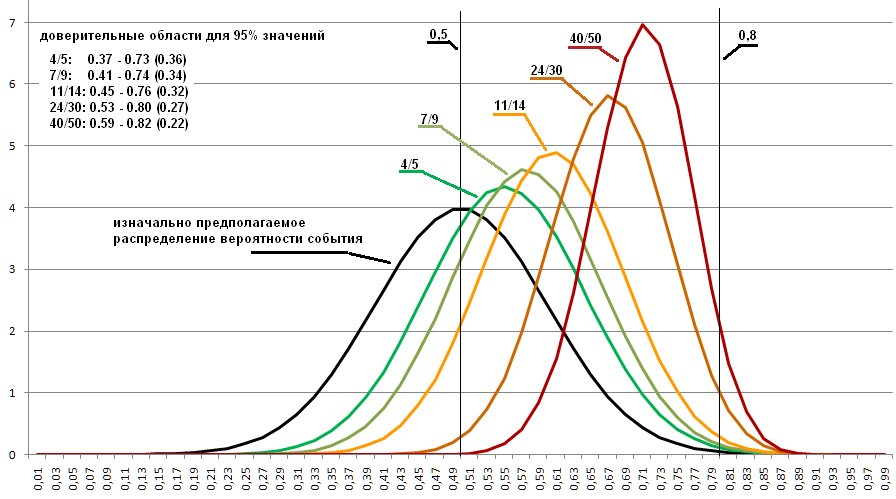
O código para esta opção está
aqui .
Pode-se ver que as distribuições mudaram fortemente e agora determinam uma região ligeiramente diferente na qual a probabilidade desejada é altamente provável. Portanto, se se sabe quais probabilidades existem para essas coisas, uma das quais queremos medir, isso pode melhorar um pouco o resultado.
Como resultado, 4/5 não significa nada e até 50 dos experimentos realizados não são muito informativos. São poucas as informações para determinar que tipo de probabilidade ainda está subjacente ao experimento.
== Atualização ==
Como
jzha mencionou nos comentários, uma pessoa que conhece matemática de maneira significativa, esses gráficos também podem ser construídos usando fórmulas exatas. Mas o objetivo deste artigo ainda é demonstrar da forma mais clara possível como é formado o que todos na vida cotidiana chama de probabilidade.
Para construí-lo usando fórmulas exatas, é necessário considerar os dados disponíveis sobre a distribuição de probabilidade de todas as moedas por meio da aproximação da distribuição beta e, calculando as distribuições, derivar os cálculos já. Esse esquema é uma quantidade substancial de explicações sobre como fazer isso e, se eu o descrever aqui, será um artigo sobre cálculos matemáticos, em vez de probabilidades diárias.
Como obter as fórmulas descritas em um caso especial com uma moeda, consulte os comentários de
jzha .