Como acelerar a descompressão LZ4 no ClickHouse?

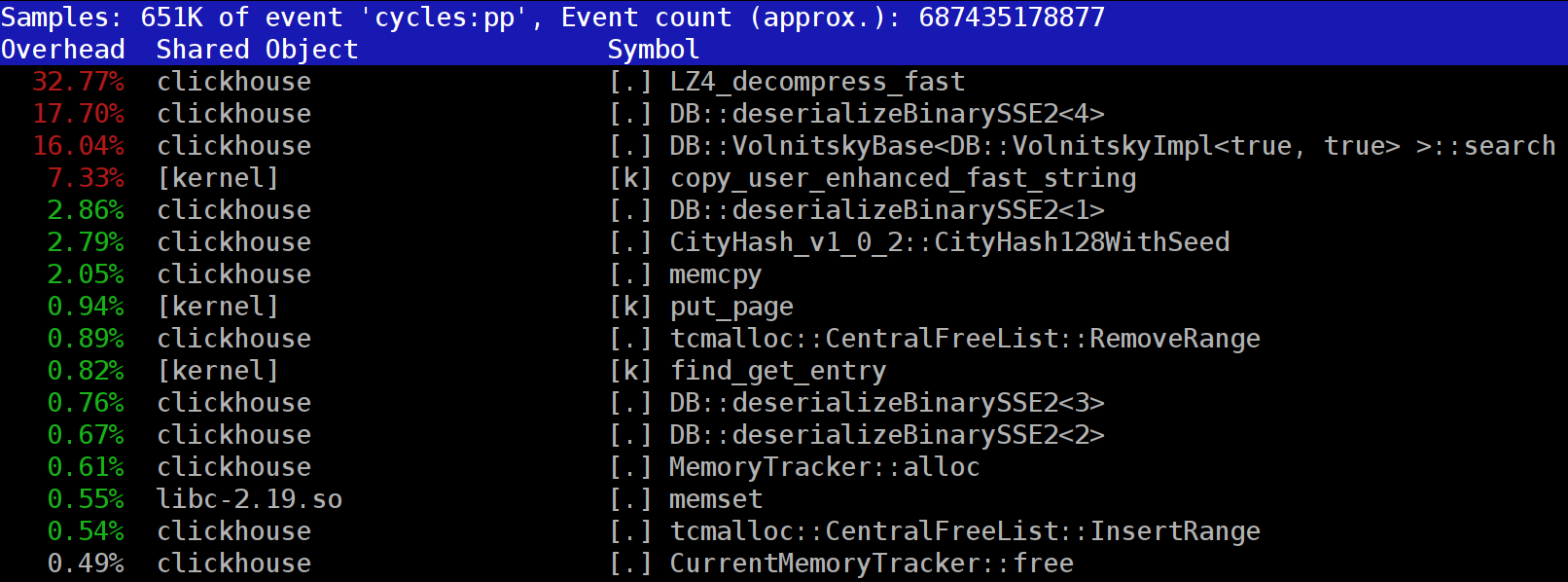
Ao executar consultas no ClickHouse , você pode perceber que o criador de perfil geralmente mostra a função LZ_decompress_fast na parte superior. O que está havendo? Essa pergunta nos fez pensar em como escolher o melhor algoritmo de compactação.

ClickHouse armazena dados em formato compactado. Ao executar consultas, o ClickHouse tenta fazer o mínimo possível, a fim de conservar os recursos da CPU. Em muitos casos, todos os cálculos potencialmente demorados já estão bem otimizados, e o usuário escreveu uma consulta bem pensada. Tudo o que resta a fazer é realizar a descompressão.



Então, por que a descompressão do LZ4 se torna um gargalo? O LZ4 parece um algoritmo extremamente leve : a taxa de descompressão de dados geralmente é de 1 a 3 GB / s por núcleo do processador, dependendo dos dados. Isso é muito mais rápido que o subsistema de disco típico. Além disso, usamos todos os núcleos de CPU disponíveis e as escalas de descompressão linearmente em todos os núcleos físicos.

No entanto, há dois pontos a serem lembrados. Primeiro, os dados compactados são lidos no disco, mas a velocidade de descompressão é fornecida em termos da quantidade de dados não compactados. Se a taxa de compactação for grande o suficiente, não haverá quase nada para ler nos discos. Mas haverá muitos dados descompactados, e isso afeta naturalmente a utilização da CPU: no caso do LZ4, a quantidade de trabalho necessária para descomprimir dados é quase proporcional ao volume dos dados descomprimidos.

Segundo, se os dados estiverem armazenados em cache, talvez você não precise ler os dados dos discos. Você pode confiar no cache da página ou usar seu próprio cache. O armazenamento em cache é mais eficiente em bancos de dados orientados a colunas, pois apenas as colunas usadas com frequência permanecem no cache. É por isso que o LZ4 geralmente parece ser um gargalo em termos de carga da CPU.

Isso traz mais duas perguntas. Primeiro, se a descompressão está nos atrasando, vale a pena compactar os dados para começar? Mas essa especulação é irrelevante na prática. Até recentemente, a configuração do ClickHouse oferecia apenas duas opções de compactação de dados - LZ4 e Zstandard . LZ4 é usado por padrão. Mudar para Zstandard torna a compactação mais forte e mais lenta. Mas não havia uma opção para desativar completamente a compactação, pois supõe-se que o LZ4 forneça uma compactação mínima razoável que sempre pode ser usada. (É exatamente por isso que eu amo LZ4.)

Mas um estranho misterioso apareceu no bate-papo internacional de suporte ClickHouse, que disse que ele tem um subsistema de disco muito rápido (com NVMe SSD) e descompactação é a única coisa que desacelera suas consultas, por isso seria bom poder armazenar dados sem compressão Respondi que não temos essa opção, mas seria fácil adicionar. Alguns dias depois, recebemos uma solicitação pull implementando o método de compactação none . Pedi ao colaborador para informar sobre o quanto essa opção ajudou a acelerar as consultas. A resposta foi que esse novo recurso acabou sendo inútil na prática, pois os dados não compactados começaram a ocupar muito espaço em disco e não se encaixavam nessas unidades NVMe.

A segunda pergunta que surge é que, se houver um cache, por que não usá-lo para armazenar dados que já estão descompactados? Esta é uma possibilidade viável que eliminará a necessidade de descompressão em muitos casos. O ClickHouse também possui um cache como este: o cache dos blocos descomprimidos . Mas é uma pena desperdiçar muita RAM nisso. Portanto, geralmente faz sentido usar em consultas pequenas e seqüenciais que usam dados quase idênticos.

Nossa conclusão é que é sempre preferível armazenar dados em formato compactado. Sempre grave dados no disco em formato compactado. Transmitir dados pela rede também com compactação. Na minha opinião, a compactação padrão é justificável mesmo quando a transferência de dados em um único datacenter em uma rede de 10 GB sem excesso de assinaturas, enquanto a transferência de dados não compactados entre datacenters é inaceitável.

Por que LZ4?

Por que escolher LZ4? Não poderíamos escolher algo ainda mais leve? Teoricamente, poderíamos, e este é um bom pensamento. Mas vejamos a classe de algoritmos aos quais o LZ4 pertence.

Primeiro de tudo, é genérico e não adapta o tipo de dados. Por exemplo, se você souber antecipadamente que terá uma matriz de números inteiros, poderá usar um dos algoritmos VarInt e isso usará a CPU com mais eficiência. Segundo, o LZ4 não depende excessivamente das suposições do modelo de dados. Digamos que você tenha uma série temporal ordenada de valores de sensores, uma matriz de números de ponto flutuante. Se você levar isso em conta, poderá calcular deltas entre esses números e depois compactá-los com o algoritmo genérico, o que resultará em uma taxa de compactação mais alta.

Você não terá problemas ao usar o LZ4 com matrizes de bytes ou arquivos. É claro que ele tem uma especialização (mais sobre isso mais tarde) e, em alguns casos, seu uso é inútil. Mas se o chamarmos de algoritmo de uso geral, estaremos bastante próximos da verdade. Devemos observar que, graças ao seu design interno, o LZ4 implementa automaticamente o algoritmo RLE como um caso especial.

No entanto, a questão mais importante é se o LZ4 é o algoritmo mais ideal dessa classe em termos de velocidade geral e força de compactação. Os algoritmos ideais são chamados de fronteira de Pareto, o que significa que não há outro algoritmo que seja definitivamente melhor de uma maneira e nem pior de outras (e também em uma ampla variedade de conjuntos de dados). Alguns algoritmos são mais rápidos, mas resultam em uma taxa de compactação menor, enquanto outros têm uma compactação mais forte, mas são mais lentos para compactar ou descomprimir.

Para ser honesto, o LZ4 não é realmente a fronteira de Pareto - existem algumas opções disponíveis que são um pouco melhores. Por exemplo, veja LZTURBO de um desenvolvedor chamado powturbo . Não há dúvida sobre a confiabilidade dos resultados, graças à comunidade encode.ru (o maior e possivelmente o único fórum sobre compactação de dados). Infelizmente, o desenvolvedor não distribui o código fonte ou os binários; eles estão disponíveis apenas para um número limitado de pessoas para testes ou por muito dinheiro (embora pareça que ainda ninguém pagou por isso). Veja também Lizard (anteriormente LZ5) e Density . Eles podem funcionar um pouco melhor que o LZ4 quando você seleciona um determinado nível de compactação. Outra opção realmente interessante é o LZSSE . Mas termine de ler este artigo antes de conferir.

Como o lz4 funciona

Vamos ver como o LZ4 funciona em geral. Esta é uma das implementações do algoritmo LZ77. L e Z representam os nomes dos desenvolvedores (Lempel e Ziv), e 77 é para o ano de 1977 quando o algoritmo foi publicado. Possui muitas outras implementações: QuickLZ, FastLZ, BriefLZ, LZF, LZO e gzip e zip se forem usados ​​baixos níveis de compactação.

Um bloco de dados compactado usando LZ4 contém uma sequência de entradas (comandos ou instruções) de dois tipos:

1. Literais: "Pegue os N bytes a seguir como estão e copie-os para o resultado".
2. Correspondência: "Retire N bytes do resultado descompactado, começando no valor de deslocamento em relação à posição atual".

Exemplo Antes da compactação:

 Hello world Hello 

Após a compactação:

 literals 12 "Hello world " match 5 12 

Se pegarmos um bloco compactado e iterarmos o cursor durante a execução desses comandos, obteremos os dados originais não compactados como resultado.

Então é assim que os dados são descompactados. A idéia básica é clara: para realizar a compactação, o algoritmo codifica uma sequência repetida de bytes usando correspondências.

Algumas características também são claras. Esse algoritmo orientado a bytes não disseca bytes individuais; apenas os copia na íntegra. É assim que difere da codificação de entropia. Por exemplo, zstd é uma combinação de LZ77 e codificação de entropia.

Observe que o tamanho do bloco compactado não deve ser muito grande. O tamanho é escolhido para evitar o desperdício de muita RAM durante a descompressão, para evitar a lentidão do acesso aleatório demais no arquivo compactado (que consiste em um grande número de blocos compactados) e, às vezes, para que o bloco caiba no cache da CPU. Por exemplo, você pode escolher 64 KB para que os buffers para dados compactados e não compactados caibam no cache L2 com metade ainda livre.

Se precisarmos compactar um arquivo maior, podemos concatenar os blocos compactados. Isso também é conveniente para armazenar dados adicionais (como uma soma de verificação) com cada bloco compactado.

O deslocamento máximo para a partida é limitado. No LZ4, o limite é de 64 kilobytes. Esse valor é chamado de janela deslizante. Isso significa que as correspondências podem ser encontradas em uma janela de 64 kilobytes que precede o cursor, que desliza com o cursor à medida que avança.

Agora vamos ver como compactar dados ou, em outras palavras, como encontrar seqüências correspondentes em um arquivo. Você sempre pode usar um sufixo trie (é ótimo se você realmente ouviu isso). Existem métodos que garantem que a correspondência mais longa esteja localizada nos bytes anteriores após a compactação. Isso é chamado de análise ideal e fornece quase a melhor taxa de compactação para um bloco compactado de formato fixo. Mas existem abordagens melhores, como encontrar uma correspondência suficientemente boa que não seja necessariamente a mais longa. A maneira mais eficiente de encontrá-lo é usando uma tabela de hash.

Para fazer isso, iteramos o cursor no bloco de dados original e pegamos alguns bytes depois do cursor (digamos 4 bytes). Nós os misturamos e colocamos o deslocamento desde o início do bloco (de onde foram retirados os 4 bytes) na tabela de hash. O valor 4 é chamado "min-match" - usando esta tabela de hash, podemos encontrar correspondências de pelo menos 4 bytes.

Se observarmos a tabela de hash e ela já tiver um registro correspondente, e o deslocamento não exceder a janela deslizante, verificamos quantos bytes mais correspondem após esses 4 bytes. Talvez haja muito mais correspondências. Também é possível que haja uma colisão na tabela de hash e nada corresponda, mas isso não é grande coisa. Você pode apenas substituir o valor na tabela de hash por um novo. As colisões na tabela de hash simplesmente levarão a uma taxa de compactação mais baixa, pois haverá menos correspondências. A propósito, esse tipo de tabela de hash (com um tamanho fixo e sem resolução de colisões) é chamado de "tabela de cache". Esse nome faz sentido porque, no caso de uma colisão, a tabela de cache simplesmente esquece a entrada antiga.

Um desafio para o leitor cuidadoso. Vamos supor que os dados sejam uma matriz de números UInt32 no formato little endian que represente parte de uma sequência de números naturais: 0, 1, 2 ... Explique por que esses dados não são compactados ao usar LZ4 (o tamanho dos dados compactados não é menor em comparação com os dados não compactados).

Como acelerar tudo

Então, eu quero acelerar a descompressão LZ4. Vamos ver como é o loop de descompressão. Aqui está no pseudocódigo:

 while (...) {    read(input_pos, literal_length, match_length);    copy(output_pos, input_pos, literal_length);    output_pos += literal_length;    read(input_pos, match_offset);    copy(output_pos, output_pos - match_offset,        match_length);    output_pos += match_length; } 

O formato LZ4 é projetado para que literais e correspondências se alternem em um arquivo compactado. Obviamente, o literal sempre vem em primeiro lugar (porque não há nenhum lugar para se combinar desde o início). Portanto, seus comprimentos são codificados juntos.

Na verdade, é um pouco mais complicado que isso. Um byte é lido do arquivo e, em seguida, é dividido em dois nibbles (meio bytes) que contêm os números codificados de 0 a 15. Se o número correspondente não for 15, presume-se que seja o comprimento do literal e da correspondência, respectivamente. E se tiver 15 anos, o comprimento será maior e será codificado nos seguintes bytes. Em seguida, o próximo byte é lido e seu valor é adicionado ao comprimento. Se for igual a 255, o mesmo será feito com o próximo byte.

Observe que a taxa máxima de compactação para o formato LZ4 não atinge 255. E outra observação inútil é que, se seus dados forem muito redundantes, o uso do LZ4 duas vezes melhorará a taxa de compactação.

Quando lemos o comprimento de um literal (e, em seguida, o comprimento e o deslocamento da correspondência), basta copiar dois blocos de memória para descompactá-lo.

Como copiar um bloco de memória

Parece que você poderia apenas usar a função memcpy , projetada para copiar blocos de memória. Mas essa não é a abordagem ideal e não é realmente apropriada.

O uso do memcpy não é ideal porque:

1. Ele geralmente está localizado na biblioteca libc (e a biblioteca libc geralmente é vinculada dinamicamente, portanto a chamada memcpy será feita indiretamente via PLT).
2. Não é incorporado pelo compilador se o argumento de tamanho for desconhecido no momento da compilação.
3. Faz muito esforço para processar corretamente as sobras de um bloco de memória que não são múltiplos do comprimento ou registro de palavras da máquina.

O último ponto é o mais importante. Digamos que pedimos à função memcpy para copiar exatamente 5 bytes. Seria ótimo copiar 8 bytes imediatamente, usando duas instruções movq.

Hello world Hello wo ...
^^^^^ ^^^ - src
^^^^^ ^^^ - dst

Mas, em seguida, copiaremos três bytes extras, e escreveremos fora dos limites do buffer. A função memcpy não tem permissão para fazer isso, porque pode sobrescrever alguns dados em nosso programa e levar a um erro de memória. E se escrevêssemos em um endereço não alinhado, esses bytes extras poderiam pousar em uma página não alocada de memória virtual ou em uma página sem acesso de gravação. Isso nos daria uma falha de segmentação (isso é bom).

Mas, no nosso caso, quase sempre podemos escrever bytes extras. Podemos ler bytes extras no buffer de entrada, desde que os bytes extras estejam localizados inteiramente dentro dele. Sob as mesmas condições, podemos gravar os bytes extras no buffer de saída, porque ainda os substituiremos na próxima iteração.

Essa otimização já está na implementação original do LZ4:

 inline void copy8(UInt8 * dst, const UInt8 * src) {    memcpy(dst, src, 8); /// Note that memcpy isn't actually called here. } inline void wildCopy8(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) {    do    {        copy8(dst, src);        dst += 8;        src += 8;    } while (dst < dst_end); } 

Para tirar proveito dessa otimização, precisamos apenas garantir que estamos longe o suficiente dos limites do buffer. Isso não deve custar nada, porque já estamos verificando o estouro de buffer. E o processamento dos últimos bytes, os dados "restantes", pode ser feito após o loop principal.

No entanto, ainda existem algumas nuances. A cópia ocorre duas vezes no loop: com um literal e uma correspondência. No entanto, ao usar a função LZ4_decompress_fast (em vez de LZ4_decompress_safe ), a verificação é realizada apenas uma vez, quando é necessário copiar o literal. A verificação não é realizada ao copiar a partida, mas a especificação para o formato LZ4 possui condições que permitem evitá-la:

Os últimos 5 bytes são sempre literais.
A última correspondência deve iniciar pelo menos 12 bytes antes do final do bloco.
Conseqüentemente, um bloco com menos de 13 bytes não pode ser compactado.

Dados de entrada especialmente selecionados podem levar à corrupção de memória. Se você usar a função LZ4_decompress_fast , precisará de proteção contra dados incorretos. No mínimo, você deve calcular somas de verificação para os dados compactados. Se você precisar de proteção contra hackers, use a função LZ4_decompress_safe . Outras opções: use uma função hash criptográfica como soma de verificação (embora isso provavelmente destrua o desempenho); alocar mais memória para buffers; aloque memória para buffers com uma chamada mmap separada e crie uma página de proteção.

Quando vejo o código que copia 8 bytes de dados, pergunto-me imediatamente por que exatamente 8 bytes. Você pode copiar 16 bytes usando registros SSE:

 inline void copy16(UInt8 * dst, const UInt8 * src) { #if __SSE2__    _mm_storeu_si128(reinterpret_cast<__m128i *>(dst),        _mm_loadu_si128(reinterpret_cast<const __m128i *>(src))); #else    memcpy(dst, src, 16); #endif } inline void wildCopy16(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) {    do    {        copy16(dst, src);        dst += 16;        src += 16;    } while (dst < dst_end); } 

O mesmo funciona para copiar 32 bytes para o AVX e 64 bytes para o AVX-512. Além disso, você pode desenrolar o loop várias vezes. Se você já examinou como o memcpy é implementado, essa é exatamente a abordagem usada. (A propósito, o compilador não desenrolará ou vetorizará o loop nesse caso, porque isso exigirá a inserção de verificações volumosas.)

Por que a implementação original do LZ4 não fez isso? Primeiro, não está claro se isso é melhor ou pior. O ganho resultante depende do tamanho dos blocos a serem copiados; portanto, se todos forem curtos, isso criaria trabalho extra por nada. E segundo, arruina as disposições no formato LZ4 que ajudam a evitar uma ramificação desnecessária no loop interno.

No entanto, manteremos essa opção em mente por enquanto.

Cópia complicada

Vamos voltar à questão de se é sempre possível copiar dados dessa maneira. Digamos que precisamos copiar uma correspondência, ou seja, pegar um pedaço de memória do buffer de saída localizado em algum deslocamento atrás do cursor e copiá-lo para a posição do cursor.

Imagine um caso simples quando você precisa copiar 5 bytes em um deslocamento de 12:

Hello world ...........
^^^^^ - src
^^^^^ - dst

Hello world Hello wo ...
^^^^^ - src
^^^^^ - dst

Mas há um caso mais difícil, quando precisamos copiar um bloco de memória maior que o deslocamento. Em outras palavras, inclui alguns dados que ainda não foram gravados no buffer de saída.

Copie 10 bytes com um deslocamento de 3:

abc .............
^^^^^^^^^^ - src
^^^^^^^^^^ - dst

abc abcabcabca ...
^^^^^^^^^^ - src
^^^^^^^^^^ - dst

Temos todos os dados durante o processo de compactação e é possível encontrar essa correspondência. A função memcpy não é adequada para copiá-la, porque não suporta o caso quando faixas de blocos de memória se sobrepõem. A função memmove também não funcionará, porque o bloco de memória que os dados devem ser extraídos ainda não foi totalmente inicializado. Precisamos copiar da mesma maneira como se estivéssemos copiando byte a byte.

 op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; ... 

Veja como funciona:

a bc a ............
^ - src
^ - dst

a b ca b ...........
^ - src
^ - dst

ab c ab c ..........
^ - src
^ - dst

abc a bc a .........
^ - src
^ - dst

abca b ca b ........
^ - src
^ - dst

Em outras palavras, devemos criar uma sequência repetida. A implementação original do LZ4 usou um código surpreendentemente estranho para fazer isso:

 const unsigned dec32table[] = {0, 1, 2, 1, 4, 4, 4, 4}; const int dec64table[] = {0, 0, 0, -1, 0, 1, 2, 3}; const int dec64 = dec64table[offset]; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += dec32table[offset]; memcpy(op+4, match, 4); match -= dec64; 

Ele copia os 4 primeiros bytes, um por um, avança por algum número mágico, copia completamente os próximos 4 bytes e move o cursor para uma correspondência usando outro número mágico. O autor do código ( Yan Collet ) se esqueceu de deixar um comentário sobre o que isso significa. Além disso, os nomes das variáveis ​​são confusos. Ambos são nomeados dec ... table, mas um é adicionado e o outro é subtraído. Além disso, um deles não é assinado e o outro é int. No entanto, o autor melhorou recentemente esse lugar no código.

Aqui está como ele realmente funciona. Copiamos os 4 primeiros bytes, um de cada vez:

abc abca .........
^^^^ - src
^^^^ - dst

Agora podemos copiar 4 bytes de uma vez:

abcabca bcab .....
^^^^ - src
^^^^ - dst

Podemos continuar como de costume, copiando 8 bytes de uma vez:

abcabcabcab cabcabca .....
^^^^^^^^ - src
^^^^^^^^ - dst

Como todos sabemos por experiência própria, às vezes a melhor maneira de entender o código é reescrevê-lo. Aqui está o que descobrimos:

 inline void copyOverlap8(UInt8 * op, const UInt8 *& match, const size_t offset) {    /// 4 % n.    /// Or if 4 % n is zero, we use n.    /// It gives an equivalent result, but is more CPU friendly for unknown reasons.    static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4 };    /// 8 % n - 4 % n    static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3 };    op[0] = match[0];    op[1] = match[1];    op[2] = match[2];    op[3] = match[3];    match += shift1[offset];    memcpy(op + 4, match, 4);    match += shift2[offset]; } 

Como esperado, isso não altera o desempenho. Eu realmente queria tentar otimização para copiar 16 bytes de uma só vez.

No entanto, isso complica o "caso especial" e faz com que seja chamado com mais frequência (a condição de offset < 16 é realizada pelo menos com a mesma frequência que o offset < 8 ). A cópia de intervalos sobrepostos com cópia de 16 bytes se parece com isso (apenas o começo mostrado):

 inline void copyOverlap16(UInt8 * op, const UInt8 *& match, const size_t offset) {    /// 4 % n.    static constexpr int shift1[]        = { 0, 1, 2, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 };    /// 8 % n - 4 % n    static constexpr int shift2[]        = { 0, 0, 0, 1, 0, -1, -2, -3, -4, 4, 4, 4, 4, 4, 4, 4 };    /// 16 % n - 8 % n    static constexpr int shift3[]        = { 0, 0, 0, -1, 0, -2, 2, 1, 8, -1, -2, -3, -4, -5, -6, -7 };    op[0] = match[0];    op[1] = match[1];    op[2] = match[2];    op[3] = match[3];    match += shift1[offset];    memcpy(op + 4, match, 4);    match += shift2[offset];    memcpy(op + 8, match, 8);    match += shift3[offset]; } 

Esta função pode ser implementada de forma mais eficaz? Gostaríamos de encontrar uma instrução SIMD mágica para um código tão complexo, porque tudo o que queremos fazer é escrever 16 bytes, que consiste inteiramente em alguns bytes de dados de entrada (de 1 a 15). Então eles só precisam ser repetidos na ordem correta.

Existe uma instrução como esta chamada pshufb (bytes de embaralhamento compactado) que faz parte do SSSE3 (três S). Ele aceita dois registros de 16 bytes. Um dos registros contém os dados de origem. O outro possui o "seletor": cada byte contém um número de 0 a 15, dependendo do byte do registro de origem para obter o resultado. Se o valor do byte do seletor for maior que 127, o byte correspondente do resultado será preenchido com zero.

Aqui está um exemplo:

  xmm0: abc .............
 xmm1: 0120120120120120

 pshufb% xmm1,% xmm0

 xmm0: abcabcabcabcabca 

Cada byte do resultado é preenchido com o byte selecionado dos dados de origem - é exatamente isso que precisamos! Aqui está a aparência do código no resultado:

 inline void copyOverlap16Shuffle(UInt8 * op, const UInt8 *& match, const size_t offset) { #ifdef __SSSE3__    static constexpr UInt8 __attribute__((__aligned__(16))) masks[] =    {        0, 1, 2, 1, 4, 1, 4, 2, 8, 7, 6, 5, 4, 3, 2, 1, /* offset = 0, not used as mask, but for shift amount instead */        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /* offset = 1 */        0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,        0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0,        0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3,        0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0,        0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3,        0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1,        0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7,        0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, 4, 5, 6,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 0, 1, 2,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 0, 1,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0,    };    _mm_storeu_si128(reinterpret_cast<__m128i *>(op),        _mm_shuffle_epi8(            _mm_loadu_si128(reinterpret_cast<const __m128i *>(match)),            _mm_load_si128(reinterpret_cast<const __m128i *>(masks) + offset)));    match += masks[offset]; #else    copyOverlap16(op, match, offset); #endif } 

Aqui _mm_shuffle_epi8 é um intrínseco , que é compilado com as instruções da CPU pshufb .

Podemos executar esta operação para mais bytes de uma vez usando instruções mais recentes? Afinal, o SSSE3 é um conjunto de instruções muito antigo que existe desde 2006. O AVX2 possui uma instrução que faz isso por 32 bytes de uma vez, mas separadamente para faixas individuais de 16 bytes. Isso é chamado de bytes permute de vetor, em vez de bytes aleatórios compactados - as palavras são diferentes, mas o significado é o mesmo. O AVX-512 VBMI possui outra instrução que funciona para 64 bytes de uma vez, mas os processadores que o suportam apareceram apenas recentemente. O ARM NEON possui instruções semelhantes chamadas vtbl (pesquisa de tabela de vetores), mas elas permitem apenas a gravação de 8 bytes.

Além disso, existe uma versão da instrução pshufb com registros MMX de 64 bits para formar 8 bytes. É o ideal para substituir a versão original do código. No entanto, decidi usar a opção de 16 bytes (por motivos sérios).

Na conferência Highload ++ Siberia, um participante veio até mim após a minha apresentação e mencionou que, para o caso de 8 bytes, você pode simplesmente usar a multiplicação por uma constante especialmente selecionada (você também precisará de um deslocamento) - isso nem havia ocorrido. para mim antes!

Como remover uma declaração if supérflua

Digamos que eu queira usar uma variante que copie 16 bytes. Como evitar a verificação adicional do estouro de buffer?

Eu decidi que simplesmente não faria essa verificação. Os comentários sobre a função dirão que o desenvolvedor deve alocar um bloco de memória para um número especificado de bytes mais do que o necessário, para que possamos ler e gravar lixo desnecessário lá. A interface da função será mais difícil de usar, mas esse é um problema diferente.

Na verdade, pode haver consequências negativas. Digamos que os dados que precisamos descomprimir foram formados a partir de blocos de 65.536 bytes cada. Em seguida, o usuário nos fornece um pedaço de memória com 65.536 bytes para os dados descomprimidos. Porém, com a nova interface de função, o usuário precisará alocar um bloco de memória com 65.551 bytes, por exemplo. Em seguida, o alocador pode ser forçado a alocar 96 ou mesmo 128 kilobytes, dependendo de sua implementação. Se o alocador estiver muito ruim, pode parar subitamente em cache a memória no "heap" e começar a usar o mmap e o munmap sempre para alocação de memória (ou liberar memória usando madvice ). Esse processo será extremamente lento devido a falhas na página. Como resultado, esse pouco de otimização pode acabar atrasando tudo.

Existe alguma aceleração?

Então, eu fiz uma versão do código que usa três otimizações:

1. Copiando 16 bytes em vez de 8.
2. Usando as instruções de reprodução aleatória para o caso de offset < 16 .
3. Removido um extra se.

Comecei a testar esse código em diferentes conjuntos de dados e obtive resultados inesperados.

Exemplo 1:
Xeon E2650v2, dados do Yandex Browser, coluna AppVersion.
Referência: 1,67 GB / seg.
16 bytes, aleatório: 2,94 GB / s (76% mais rápido).

Exemplo 2:
Xeon E2650v2, dados Yandex Direct, coluna ShowsSumPosition.
Referência: 2,30 GB / seg.
16 bytes, aleatório: 1,91 GB / s (20% mais lento).

Fiquei muito feliz no começo, quando vi que tudo havia acelerado em uma porcentagem tão grande. Então vi que nada era mais rápido com outros arquivos. Foi um pouco mais lento para alguns deles. Concluí que os resultados dependem da taxa de compressão. Quanto mais compactado o arquivo, maior a vantagem de mudar para 16 bytes. Isso parece natural: quanto maior a taxa de compactação, maior o comprimento médio dos fragmentos a serem copiados.

Para investigar, usei modelos C ++ para fazer opções de código para quatro casos: usando pedaços de 8 ou 16 bytes e com ou sem a instrução de reprodução aleatória.

 template <size_t copy_amount, bool use_shuffle> void NO_INLINE decompressImpl(    const char * const source,    char * const dest,    size_t dest_size) 

Variantes completamente diferentes do código tiveram um desempenho melhor em arquivos diferentes, mas ao testar em uma área de trabalho, a versão com shuffle sempre venceu. Testar em uma área de trabalho é inconveniente porque você precisa fazer isso:

 sudo echo 'performance' | tee /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor kill -STOP $(pidof firefox) $(pidof chromium) 

Então eu fui em um dos antigos servidores de "desenvolvimento" (com o processador Xeon E5645), peguei ainda mais conjuntos de dados e obtive resultados quase opostos, o que me confundiu totalmente. Acontece que a escolha do algoritmo ideal depende do modelo do processador, além da taxa de compressão. O processador determina quando é melhor usar a instrução aleatória, bem como o limite para quando começar a usar a cópia de 16 bytes.

A propósito, ao testar em nossos servidores, faz sentido fazer isso:

 sudo kill -STOP $(pidof python) $(pidof perl) $(pgrep -u skynet) $(pidof cqudp-client) 

Caso contrário, os resultados serão instáveis. Também tenha cuidado com a aceleração térmica e o limite de potência.

Como escolher o melhor algoritmo

Portanto, temos quatro variantes do algoritmo e precisamos escolher a melhor para as condições. Poderíamos criar um conjunto representativo de dados e hardware, realizar testes de carga sérios e escolher o melhor método, em média. Mas não temos um conjunto de dados representativo. Para o teste, usei uma amostra de dados do Yandex Metrica , Yandex Direct, Yandex Browser e voos nos Estados Unidos . Mas isso não é suficiente, porque o ClickHouse é usado por centenas de empresas em todo o mundo. Ao otimizar demais um conjunto de dados, podemos causar uma queda no desempenho com outros dados e nem percebê-lo. E se os resultados dependerem do modelo do processador, teremos que escrever explicitamente as condições no código e testá-lo em cada modelo (ou consultar o manual de referência sobre instruções de tempo, o que você acha?). Em ambos os casos, isso consome muito tempo.

Por isso, decidi usar outro método, o que é óbvio para os colegas que estudaram em nossa Escola de Análise de Dados: "bandidos armados" . O ponto é que a variante do algoritmo é escolhida aleatoriamente e, em seguida, usamos a estatística para escolher progressivamente mais frequentemente as opções com melhor desempenho.

Como temos muitos blocos de dados que precisam ser descompactados, precisamos de chamadas de função independentes para descomprimir dados. Poderíamos escolher um dos quatro algoritmos para cada bloco e medir seu tempo de execução. Uma operação como essa geralmente não custa nada em comparação com o processamento de um bloco de dados e, no ClickHouse, um bloco de dados não compactados tem pelo menos 64 KB. (Leia este artigo sobre como medir o tempo.)

Para entender melhor como o algoritmo de "bandidos multi-armados" funciona, vejamos de onde vem o nome. Esta é uma analogia com as máquinas caça-níqueis em um cassino que possuem várias alavancas que um jogador pode usar para obter uma quantia aleatória de dinheiro. O jogador pode puxar as alavancas várias vezes em qualquer ordem. Cada alavanca tem uma probabilidade fixa para a quantidade correspondente de dinheiro distribuída, mas o jogador não sabe como funciona e só pode aprender com a experiência de jogar o jogo. Depois de descobrir, eles podem maximizar seus ganhos.

Uma abordagem para maximizar a recompensa é avaliar a distribuição de probabilidade de cada alavanca em cada etapa, com base nas estatísticas do jogo das etapas anteriores. Então "mentalmente" ganhamos uma recompensa aleatória para cada alavanca, com base nas distribuições recebidas. Finalmente, puxamos a alavanca que teve o melhor resultado em nosso jogo mental. Essa abordagem é chamada Thompson Sampling.

Mas estamos escolhendo um algoritmo de descompressão. O resultado é o tempo de execução em picossegundos por byte: quanto menos, melhor. Vamos considerar o tempo de execução como uma variável aleatória e avaliar sua distribuição usando estatísticas matemáticas. A abordagem bayesiana é frequentemente usada para tarefas como essa, mas seria complicado inserir fórmulas complexas no código C ++. Podemos usar uma abordagem paramétrica e dizer que uma variável aleatória pertence a uma família paramétrica de variáveis ​​aleatórias e depois avaliar seus parâmetros.

Como selecionamos a família de variáveis ​​aleatórias? Como exemplo, podemos supor que o tempo de execução do código tenha distribuição normal. Mas isso está absolutamente errado. Primeiro, o tempo de execução não pode ser negativo e a distribuição normal leva valores para todos os lugares da linha numérica. Segundo, presumo que o tempo de execução terá uma "cauda" pesada na extremidade direita.

No entanto, existem fatores que podem tornar uma boa idéia estimar a distribuição normal apenas para os fins da Thompson Sampling (apesar do fato de que a distribuição da variável de destino não é necessariamente normal). A razão para isso é que é muito fácil calcular a expectativa matemática e a variação e, após um número suficiente de iterações, uma distribuição normal se torna bastante estreita, não muito diferente das distribuições que teríamos obtido usando outros métodos. Se não estamos muito preocupados com a taxa de convergência nas primeiras etapas, esses detalhes podem ser ignorados.

This may seem like a somewhat ignorant approach. Experience has shown us that the average time for query execution, website page loading, and so on is "garbage" that isn't worth calculating. It would be better to calculate the median, which is a robust statistic . But this is a little more difficult, and as I will show later, the described method justifies itself for practical purposes.

At first I implemented calculation of the mathematical expectation and variance, but then I decided that this is too good, and I need to simplify the code to make it "worse":

 /// For better convergence, we don't use proper estimate of stddev. /// We want to eventually separate the two algorithms even in cases /// when there is no statistical significant difference between them. double sigma() const {    return mean() / sqrt(adjustedCount()); } double sample(pcg64 & rng) const {    ...    return std::normal_distribution<>(mean(), sigma())(rng); } 

I wrote it so that the first few iterations were not taken into account, to eliminate the effect of memory latencies.

The result is a test program that can select the best algorithm for the input data, with optional modes that use the reference implementation of LZ4 or a specific version of the algorithm.

So there are six options:
— Reference (baseline): original LZ4 without our modifications.
— Variant 0: copy 8 bytes at a time without shuffle.
— Variant 1: copy 8 bytes at a time with shuffle.
— Variant 2: copy 16 bytes at a time without shuffle.
— Variant 3: copy 16 bytes at a time with shuffle.
— The "bandit" option, which selects the best of the four optimized variants.

Testing on different CPUs

If the result strongly depends on the CPU model, it would be interesting to find out exactly how it is affected. There might be an exceptionally large difference on certain CPUs.

I prepared a set of datasets from different tables in ClickHouse with real data, for a total of 256 different files each with 100 MB of uncompressed data (the number 256 was coincidental). Then I looked at the CPUs of the servers where I can run benchmarks. I found servers with the following CPUs:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz

The most interesting part comes next — the processors provided by the R&D department:
— AMD EPYC 7351 16-Core Processor, a new AMD server processor.
— Cavium ThunderX2, which is AArch64, not x86. For these, my SIMD optimization needed to be reworked a bit. The server has 224 logical and 56 physical cores.

There are 13 servers in total, and each of them runs the test on 256 files in 6 variants (reference, 0, 1, 2, 3, adaptive). The test is run 10 times, alternating between the options in random order. It outputs 199,680 results that we can compare.

For example, we can compare different CPUs with each other. But we shouldn't jump to conclusions from these results, because we are only testing the LZ4 decompression algorithm on a single core (this is a very narrow case, so we only get a micro-benchmark). For example, the Cavium has the lowest performance per single core. But I tested ClickHouse on it myself, and it wins out over Xeon E5-2650 v2 on heavy queries due to the greater number of cores, even though it is missing many optimizations that are made in ClickHouse specifically for the x86.

 ┌─cpu───────────────────┬──ref─┬─adapt─┬──max─┬─best─┬─adapt_boost─┬─max_boost─┬─adapt_over_max─┐
│ E5-2667 v2 @ 3.30GHz │ 2.81 │ 3.19 │ 3.15 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2650 v2 @ 2.60GHz │ 2.5 │ 2.84 │ 2.81 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2683 v4 @ 2.10GHz │ 2.26 │ 2.63 │ 2.59 │ 3 │ 1.16 │ 1.15 │ 1.02 │
│ E5-2660 v4 @ 2.00GHz │ 2.15 │ 2.49 │ 2.46 │ 3 │ 1.16 │ 1.14 │ 1.01 │
│ AMD EPYC 7351 │ 2.03 │ 2.44 │ 2.35 │ 3 │ 1.20 │ 1.16 │ 1.04 │
│ E5-2660 0 @ 2.20GHz │ 2.13 │ 2.39 │ 2.37 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E312xx (Sandy Bridge) │ 1.97 │ 2.2 │ 2.18 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E5530 @ 2.40GHz │ 1.65 │ 1.93 │ 1.94 │ 3 │ 1.17 │ 1.18 │ 0.99 │
│ E5645 @ 2.40GHz │ 1.65 │ 1.92 │ 1.94 │ 3 │ 1.16 │ 1.18 │ 0.99 │
│ AMD Opteron 6380 │ 1.47 │ 1.58 │ 1.56 │ 1 │ 1.07 │ 1.06 │ 1.01 │
│ AMD Opteron 6274 │ 1.15 │ 1.35 │ 1.35 │ 1 │ 1.17 │ 1.17 │ 1 │
│ E5440 @ 2.83GHz │ 1.35 │ 1.33 │ 1.42 │ 1 │ 0.99 │ 1.05 │ 0.94 │
│ Cavium ThunderX2 │ 0.84 │ 0.87 │ 0.87 │ 0 │ 1.04 │ 1.04 │ 1 │
└───────────────────────┴──────┴───────┴──────┴──────┴─────────────┴───────────┴────────────────┘ 

• ref, adapt, max — The speed in gigabytes per second (the value that is the reverse of the arithmetic mean of time for all launches on all datasets).
• best — The number of the best algorithm among the optimized variants, from 0 to 3.
• adapt_boost — The relative advantage of the adaptive algorithm compared to the baseline.
• max_boost — The relative advantage of the best of the non-adaptive variants compared to the baseline.
• adapt_over_max — The relative advantage of the adaptive algorithm over the best non-adaptive one.

The results show that we were able to speed up decompression by 12-20% on modern x86 processors. Even on ARM we saw 4% improvement, despite the fact that we didn't optimize much for this architecture. It is also clear that on average for different datasets, the "bandit" algorithm comes out ahead of the pre-selected best variant on all processors (except for very old Intel CPUs).

Conclusão

In practice, the usefulness of this work is dubious. Yes, LZ4 decompression was accelerated on average by 12-20%, and on some datasets the performance more than doubled. But in general, this doesn't have much effect on query execution time. It's difficult to find real queries that gain more than a couple percent in speed.

We decided to use ZStandard level 1 instead of LZ4 on several Yandex Metrica clusters intended for executing long queries, because it is more important to save IO and disk space on cold data. Keep this in mind if you have similar workload.

We observed the greatest benefits from optimizing decompression in highly compressible data, such as columns with mostly duplicate string values. However, we have developed a separate solution specifically for this scenario that allows us to significantly speed up queries over this kind of data.

Another point to remember is that optimization of decompression speed is often limited by the format of the compressed data. LZ4 uses a very good format, but Lizard, Density and LZSSE have other formats that can work faster. Perhaps instead of trying to accelerate LZ4, it would be better to just integrate LZSSE into ClickHouse.

It's unlikely that these optimizations will be implemented in the mainstream LZ4 library: in order to use them, the library interface would have to be modified. In fact, this is often the case with improving algorithms — optimizations don't fit into old abstractions and they have to be revised. However, variable names have already been corrected in the original implementation. For instance, inc and dec tables have been corrected . In addition, about a month ago, the original implementation accelerated decompression by the same 12-15% by copying 32 bytes instead of 16, as discussed above. We tried the 32-byte option ourselves and the results were not that great, but they were still faster .

If you look at the profile at the beginning of the article, you may notice that we could have removed one extra copying operation from the page cache to userspace (either using mmap , or using O_DIRECT and userspace page cache, but both options are problematic). We also could have slightly improved the checksum calculation (CityHash128 is currently used without CRC32-C, but we could use HighwayHash, FARSH or XXH3). Acceleration of these two operations is useful for weakly compressed data, since they are performed on compressed data.

In any case, the changes have already been added to master more than a year ago, and the ideas that resulted from this research have been applied in other tasks. You can also watch the video from HighLoad++ Siberia, or view the presentation (both in Russian).