A propriedade de simetria da relação de cointegração

O objetivo deste artigo é compartilhar resultados paradoxais no estudo da co-integração de séries temporais : se as séries temporais $$$A$ co-integrado com as proximidades $$$B$ linha $$$B$ nem sempre co-integrado com um número $$$A$ .

Se estudarmos a cointegração puramente teoricamente, é fácil provar que, se a série $$$A$ co-integrado com $$$B$ então remar $$$B$ co-integrado com $$$A$ . No entanto, se começamos a estudar a cointegração empiricamente, verifica-se que os cálculos teóricos nem sempre são confirmados. Por que isso está acontecendo?

Simetria

Atitude $$$A$ chamado simétrico se $$$A \ subseteq A ^ {- 1}$ onde $$$A ^ {- 1}$ - a razão inversa definida pela condição: $$$x A ^ {- 1} e$ equivalente a $$$yAx$ . Em outras palavras, se a relação $$$xAy$ então a relação $$$yAx$ .

Considere dois $$$I (1)$ um número de $$$x_t$ e $$$y_t$ , $$$t = 0, \ pontos, T$ . A cointegração é simétrica se $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ implica $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ isto é, se a presença de regressão direta leva à presença do inverso.

Considere a equação $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ , $$$\ beta_1 \ neq 0$ . Troque os lados esquerdo e direito e subtraia $$$\ varepsilon_ {1t}$ de ambas as partes: $$$\ beta_1 x_t = y_t - \ varepsilon_ {1t}$ . Desde $$$\ beta_1 \ neq 0$ por definição, divida as duas partes em $$$\ beta_1$ :

$$

$$x_t = \ frac {1} {\ beta_1} y_t - \ frac {\ varepsilon_ {1t}} {\ beta_1}.$$

Substitua $$$1 / \ beta_1$ em $$$\ beta_2$ e $$$- \ varepsilon_ {1t} / \ beta_1$ em $$$\ varepsilon_ {2t}$ nós temos $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ . Portanto, a relação de cointegração é simétrica.

Daqui resulta que se a variável $$$X$ cointegrado com variável $$$Y$ então a variável $$$Y$ deve ser co-integrado com a variável $$$X$ . No entanto, o teste de cointegração de Angle-Granger nem sempre confirma essa propriedade de simetria, pois às vezes uma variável $$$Y$ não co-integrado com variável $$$X$ de acordo com este teste.

Testei a propriedade de simetria nos dados de 2017 das trocas de Moscou e Nova York usando o teste de Angle-Granger. Havia 7.975 pares de ações co-integrados na Bolsa de Moscou. Para 7731 (97%) pares cointegrados, a propriedade de simetria foi confirmada; para 244 (3%) pares cointegrados, a propriedade de simetria não foi confirmada.

Havia 140.903 pares de ações co-integrados na Bolsa de Nova York. Para 136586 (97%) pares cointegrados, a propriedade de simetria foi confirmada, para 4317 (3%) pares cointegrados, a propriedade de simetria não foi confirmada.

Interpretação

Esse resultado pode ser interpretado pela baixa potência e alta probabilidade de erro do segundo tipo do teste de Dickey-Fuller, no qual o teste de Angle-Granger se baseia. A probabilidade de um erro do segundo tipo pode ser denotada por $$$\ beta = P (H_0 | H_1)$ então o valor $$ chamado o poder do teste. Infelizmente, o teste Dickey-Fuller não consegue distinguir séries temporais não estacionárias e quase não estacionárias.

O que é uma série temporal quase instável? Considere a série temporal $$$x_t = \ phi x_ {t-1} + \ varepsilon_t$ . Uma série temporal estacionária é uma série em que $$$0 <\ phi <1$ . Uma série temporal não estacionária é uma série em que $$$\ phi = 1$ . Uma série temporal quase instável é uma série em que o valor $$$\ phi$ perto de um.

No caso de séries temporais quase não estacionárias, geralmente não somos capazes de rejeitar a hipótese nula de não estacionária. Isso significa que o teste Dickey-Fuller apresenta um alto risco de um erro de segundo tipo, ou seja, a probabilidade de não rejeitar a hipótese nula falsa.

Teste KPSS

Uma possível resposta à fraqueza do teste de Dickey-Fuller é o teste KPSS, que deve esse nome às iniciais dos cientistas de Kvyatkovsky, Phillips, Schmidt e Sheen. Embora a abordagem metodológica deste teste seja completamente diferente da abordagem de Dickey-Fuller, a principal diferença deve ser entendida na permutação das hipóteses nulas e alternativas.

No teste KPSS, a hipótese nula afirma que a série temporal é estacionária, versus a alternativa sobre a presença de não estacionariedade. Séries temporais quase não estacionárias, que muitas vezes foram identificadas como não estacionárias usando o teste Dickey-Fuller, podem ser corretamente identificadas como estacionárias usando o teste KPSS.

No entanto, devemos estar cientes de que quaisquer resultados de testes estatísticos são meramente probabilísticos e não devem ser confundidos com um certo julgamento verdadeiro. Sempre existe uma probabilidade diferente de zero de que estamos enganados. Por esse motivo, propõe-se combinar os resultados dos testes Dickey-Fuller e KPSS como um teste ideal para não estacionariedade.



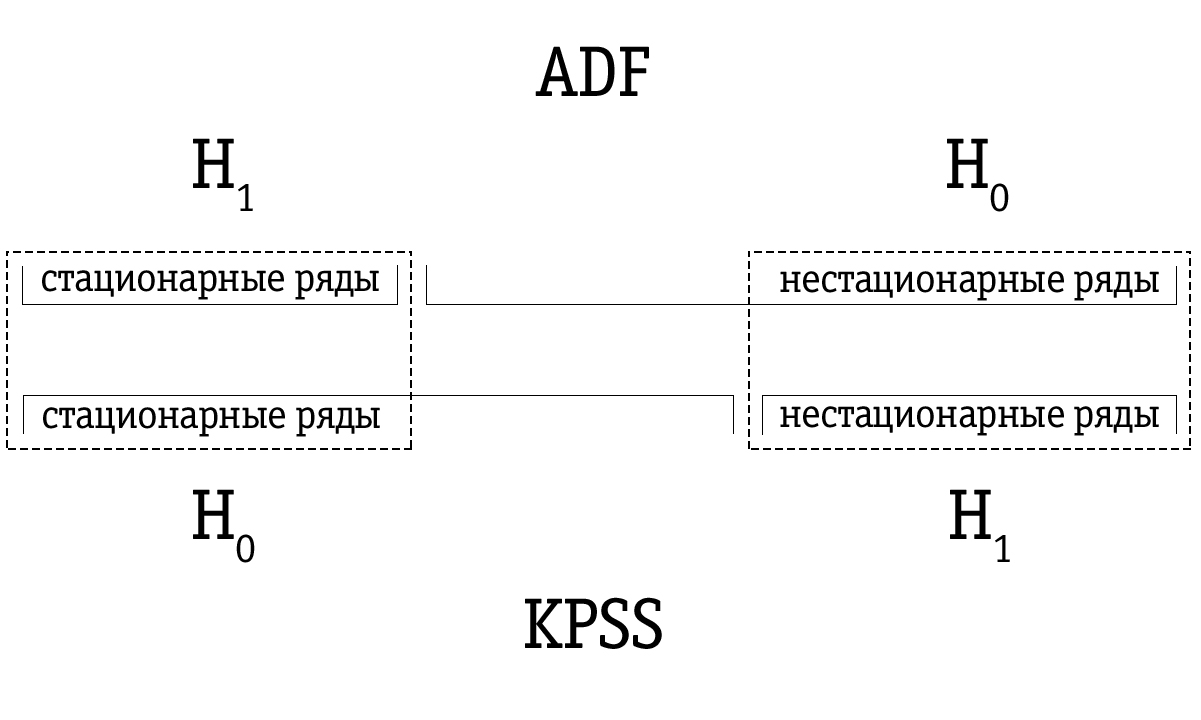
Devido à baixa potência, o teste Dickey-Fuller geralmente identifica erroneamente uma série como não estacionária, portanto, o conjunto de séries temporais resultante identificado pelo teste Dickey-Fuller como instável acaba sendo maior em comparação com muitas séries temporais identificadas como não estacionárias usando o teste KPSS. Portanto, a ordem de teste é importante.

Se a série temporal for identificada como estacionária usando o teste Dickey-Fuller, provavelmente também será identificada como estacionária usando o teste KPSS; neste caso, podemos assumir que a série é realmente estacionária.

Se a série temporal foi identificada como instável usando o teste KPSS, provavelmente também será identificada como instável usando o teste Dickey-Fuller; neste caso, podemos assumir que a série é realmente instável.

No entanto, muitas vezes acontece que uma série cronológica identificada como não estacionária usando o teste Dickey-Fuller será marcada como estacionária usando o teste KPSS. Nesse caso, devemos ter muito cuidado com nossa conclusão final. Podemos verificar o quão forte é a base da estacionariedade no caso do teste KPSS e a instabilidade no caso do teste Dickey-Fuller e tomar uma decisão apropriada. Obviamente, também podemos deixar a questão da estacionariedade de uma série temporal desse tipo sem solução.

A abordagem de teste KPSS assume séries temporais $$$y_t$ testado quanto à estacionariedade em relação a uma tendência pode ser decomposto na soma de uma tendência determinística $$$\ beta t$ passeio aleatório $$$r_t$ e erro estacionário $$$\ varepsilon_t$ :

$$

$$y_t = \ beta t + r_t + \ varepsilon_t, \\ r_t = r_ {t-1} + u_t,$$

onde $$$u_t$ - processo de identificação normal com média e variância zero $$$\ sigma ^ 2$ ( $$$u_t \ sim N (0, \ sigma ^ 2)$ ) Valor inicial $$$r_0$ tratado como fixo e desempenha o papel de membro livre. Erro estacionário $$$\ varepsilon_t$ pode ser gerado por qualquer processo ARMA comum, ou seja, pode ter forte autocorrelação.

Semelhante ao teste de Dickey-Fuller, a capacidade de levar em conta uma estrutura arbitrária de autocorrelação $$$\ varepsilon_t$ muito importante porque a maioria das séries temporais econômicas depende muito do tempo e, portanto, possui uma forte autocorrelação. Se quisermos verificar a estacionariedade em relação ao eixo horizontal, o termo $$$\ beta t$ apenas excluído da equação acima.

A partir da equação acima, segue-se que a hipótese nula $$$H_0$ sobre estacionariedade $$$y_t$ equivalente à hipótese $$$\ sigma ^ 2 = 0$ , a partir do qual se segue $$$r_t = r_0$ para todos $$$t$ ( $$$r_0$ É uma constante). Da mesma forma, uma hipótese alternativa $$$H_1$ não estacionariedade é equivalente à hipótese $$$\ sigma ^ 2 \ neq 0$ .

Para testar a hipótese $$$H_0$ : $$$\ sigma ^ 2 = 0$ (séries temporais estacionárias) versus alternativas $$$H_1$ : $$$\ sigma ^ 2 \ neq 0$ (séries temporais não estacionárias) os autores do teste KPSS recebem estatísticas unidirecionais do teste multiplicador de Lagrange. Eles também calculam sua distribuição assintótica e modelam os valores críticos assintóticos. Não consideramos detalhes teóricos aqui, mas apenas descrevemos brevemente o algoritmo de execução de teste.

Ao executar o teste KPSS para uma série temporal $$$y_t$ , $$$t = 1, \ pontos, T$ o método dos mínimos quadrados (mínimos quadrados) é usado para estimar uma das seguintes equações:

$$

$$y_t = a_0 + \ varepsilon_t, \\ y_t = a_0 + \ beta t + \ varepsilon_t.$$

Se queremos verificar a estacionariedade em relação ao eixo horizontal, avaliamos a primeira equação. Se planejamos verificar a estacionariedade em relação à tendência, escolhemos a segunda equação.

Sobras $$$e_t$ da equação estimada são usados ​​para calcular as estatísticas do teste dos multiplicadores de Lagrange. O teste do multiplicador de Lagrange é baseado na idéia de que, quando a hipótese nula for cumprida, todos os multiplicadores de Lagrange deverão ser iguais a zero.

Teste multiplicador de Lagrange

O teste multiplicador de Lagrange está associado a uma abordagem mais geral da estimativa de parâmetros, usando o método da máxima verossimilhança (ML). De acordo com essa abordagem, os dados são considerados evidências relacionadas aos parâmetros de distribuição. A evidência é expressa como uma função de parâmetros desconhecidos - uma função de probabilidade:

$$

$$L (X_1, X_2, X_3, \ pontos, X_n; \ Phi_1, \ Phi_2, \ pontos, \ Phi_k),$$

onde $$$X_i$ Os valores observados e $$$\ Phi_i$ - parâmetros que queremos avaliar.

A função de máxima verossimilhança é a probabilidade conjunta de observações amostrais.

$$

$$L (X_1, X_2, X_3, \ pontos, X_n; \ Phi_1, \ Phi_2, \ pontos, \ Phi_k) = P (X_1 \ terreno X_2 \ terreno X_3 \ pontos X_n).$$

O objetivo do método de máxima verossimilhança é maximizar a função de verossimilhança. Isso é obtido diferenciando a função de probabilidade máxima para cada um dos parâmetros estimados e equiparando as derivadas parciais a zero. Os valores dos parâmetros nos quais o valor da função é máximo é a estimativa desejada.

Geralmente, para simplificar o trabalho subseqüente, o logaritmo da função de probabilidade é primeiro obtido.

Considere um modelo linear generalizado $$$Y = \ beta X + \ varepsilon$ onde se assume que $$$\ varepsilon$ normalmente distribuído $$$N (0, \ sigma ^ 2)$ isso é $$$Y - \ beta X \ sim N (0, \ sigma ^ 2)$ .

Queremos testar a hipótese de que o sistema $$$q$ ( $$$q <k$ ) restrições lineares independentes $$$R \ beta = r$ . Aqui $$$R$ - famoso $$$q \ vezes k$ matriz de classificação $$$q$ e $$$r$ - famoso $$$q \ vezes 1$ vetor.

Para cada par de valores observados $$$X$ e $$$Y$ em condições normais, uma função de densidade de probabilidade da seguinte forma existirá:

$$

$$f (X_i, Y_i) = \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2}.$$

Sujeito a $$$n$ observações conjuntas $$$X$ e $$$Y$ a probabilidade total de observar todos os valores na amostra é igual ao produto dos valores individuais da função densidade de probabilidade. Assim, a função de probabilidade é definida da seguinte maneira:

$$

$$L (\ beta) = \ prod \ limits_ {i = 1} ^ n \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {1} {2} \ left (\ frac {Y_i - \ beta X_i} {\ sigma} \ right) ^ 2}.$$

Como é mais fácil diferenciar a soma do que o produto, o logaritmo da função de verossimilhança é geralmente usado, assim:

$$

$$\ ln L (\ beta) = \ sum \ limits_ {i = 1} ^ n \ left (\ ln \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} - \ frac {1} { 2 \ sigma ^ 2} (Y_i - \ beta X_i) ^ 2 \ direita).$$

Essa conversão útil não afeta o resultado final, porque $$$\ ln L$ É uma função crescente $$$L$ . Então o valor $$$\ beta$ o que maximiza $$$\ ln L$ também irá maximizar $$$L$ .

Pontuação ML para $$$\ beta$ em regressão com restrição ( $$$R \ beta = r$ ) é obtido maximizando a função $$$\ ln L (\ beta)$ sujeito a $$$R \ beta = r$ . Para encontrar essa estimativa, escrevemos a função Lagrange:

$$

$$\ psi (\ beta) = \ ln L (\ beta) - g '(R \ beta - r),$$

onde através $$$g = \ left (g_1, \ dots, g_q \ right) '$ vetor marcado $$$q$ Multiplicadores de Lagrange.

Estatísticas de teste do multiplicador de Lagrange indicadas por $$$\ eta_ \ mu$ em caso de estacionariedade em relação ao eixo horizontal e através $$$\ eta_ \ tau$ no caso de estacionariedade relativa à tendência, é determinada pela expressão

$$

$$\ eta _ {\ mu / \ tau} = T ^ 2 \ frac {1} {s ^ 2 (l)} \ sum \ limits_ {t = 1} ^ T S_t ^ 2,$$

onde

$$

$$S_t = \ soma \ limites_ {i = 1} ^ t e_i$$

e

$$

$$s ^ 2 (l) = T ^ {- 1} \ soma \ limites_ {t = 1} ^ T e_t ^ 2 + 2 T ^ {- 1} \ soma \ limites_ {1} ^ lw (s, l) \ sum \ limits_ {t = s + 1} ^ T e_t e_ {ts},$$

onde

$$

$$w (s, l) = 1 - \ frac {s} {l + 1}.$$

Nas equações acima $$$S_t$ - o processo de saldos parciais $$$e_t$ da equação estimada; $$$s ^ 2 (l)$ - avaliação da dispersão a longo prazo de resíduos $$$e_t$ ; mas $$$w (s, l)$ - a chamada janela espectral de Bartlett, onde $$$l$ - parâmetro de truncamento de atraso.

Nesta aplicação, a janela espectral é usada para estimar a densidade espectral de erros para um determinado intervalo (janela), que se move ao longo de toda a faixa da série. Dados fora do intervalo são ignorados, pois a função window é igual a zero fora de algum intervalo selecionado (window).

Estimativa de Variância $$$s ^ 2 (l)$ depende do parâmetro $$$l$ e desde $$$l$ aumenta e mais de 0, pontuação $$$s ^ 2 (l)$ começa a considerar uma possível autocorrelação em resíduos $$$e_t$ .

Finalmente, as estatísticas de teste do multiplicador Lagrange $$$\ eta_ \ mu$ ou $$$\ eta_ \ tau$ compara com valores críticos. Se as estatísticas do teste multiplicador de Lagrange excederem o valor crítico correspondente, a hipótese nula $$$H_0$ (séries temporais estacionárias) diverge em favor de uma hipótese alternativa $$$H_1$ (séries temporais não estacionárias). Caso contrário, não podemos rejeitar a hipótese nula $$$H_0$ sobre estacionariedade de uma série temporal.

Os valores críticos são assintóticos e, portanto, são mais adequados para amostras grandes. No entanto, na prática, eles também são usados ​​para uma pequena amostra. Além disso, os valores críticos são independentes do parâmetro $$$l$ . No entanto, as estatísticas do teste multiplicador de Lagrange dependerão do parâmetro $$$l$ . Os autores do teste KPSS não oferecem nenhum algoritmo geral para escolher o parâmetro apropriado. $$$l$ . O teste geralmente é realizado para $$$l$ no intervalo de 0 a 8.

Com aumento $$$l$ é menos provável que rejeitemos a hipótese nula $$$H_0$ sobre estacionariedade, que parcialmente leva a uma diminuição no poder do teste e pode gerar resultados contraditórios. No entanto, em geral, podemos dizer que se a hipótese nula $$$H_0$ estacionariedade da série temporal não é rejeitada, mesmo em valores pequenos $$$l$ (0, 1 ou 2), concluímos que as séries temporais verificadas são estacionárias.

Comparação dos resultados dos testes

A metodologia a seguir foi desenvolvida para avaliar a probabilidade de simetria.

1. Todas as séries temporais são verificadas quanto à integrabilidade de 1ª ordem, usando o teste Dickey-Fuller no nível de significância de 0,05. Somente séries integráveis ​​de primeira ordem são consideradas abaixo.
2. As séries integráveis ​​de primeira ordem obtidas na Seção 1 compreendem pares combinando sem repetição.
3. Os pares de ações estabelecidos na cláusula 2 são testados quanto à cointegração usando o teste de Angle-Granger. Como resultado, pares cointegrados são identificados.
4. Os resíduos de regressão obtidos como resultado do teste no parágrafo 3 são testados quanto à estacionariedade usando o teste KPSS. Assim, os resultados dos dois testes são combinados.
5. As séries temporais nos pares cointegrados da Seção 2 são trocadas e verificadas novamente quanto à cointegração usando o teste de Angle-Granger, ou seja, examinamos se a relação entre séries temporais é simétrica.
6. As séries temporais nos pares co-integrados do item 4 são trocadas e os resíduos da regressão são verificados novamente quanto à estacionariedade usando o teste KPSS, ou seja, examinaremos se a relação entre as séries temporais é simétrica.

Todos os cálculos são realizados usando o pacote MATLAB. Os resultados são apresentados na tabela abaixo. Para cada teste, temos várias relações simétricas de acordo com os resultados do teste (marcadas $$$S$ ); temos vários relacionamentos que não são simétricos de acordo com os resultados do teste (marcados $$$¬S$ ); e temos uma probabilidade empírica de que a proporção seja simétrica de acordo com os resultados do teste ( $$$P (S) = \ frac {S} {S + ¬S}$ )

Na Bolsa de Moscou:


Na Bolsa de Nova York:

Comparação de resultados de backtest

Vamos comparar os resultados de uma estratégia de negociação de dados históricos para pares co-integrados selecionados usando o teste Angle-Granger e para pares co-integrados selecionados usando o teste KPSS.

Como se pode observar na tabela, devido a uma identificação mais precisa dos pares de ações co-integrados, foi possível aumentar o rendimento médio anual ao negociar um par co-integrado separado em 9,21%. Assim, a metodologia proposta pode aumentar a lucratividade da negociação algorítmica usando estratégias neutras de mercado.

Interpretação alternativa

Como vimos acima, os resultados do teste de Angle-Granger são uma loteria. Para alguns, meus pensamentos parecerão excessivamente categóricos, mas acho que faz muito sentido não adotar a hipótese nula, confirmada pela análise estatística, sobre fé.

O conservadorismo do método científico para testar hipóteses é que, ao analisar os dados, podemos apenas fazer uma conclusão válida: a hipótese nula é rejeitada no nível de significância selecionado. Isso não significa que a alternativa seja verdadeira. $$$H_1$ - acabamos de receber evidências indiretas de sua credibilidade com base em uma típica "evidência do contrário". No caso em que é verdade $$$H_0$ , o pesquisador também é instruído a concluir cautelosamente: com base nos dados obtidos nas condições experimentais, não foi possível encontrar evidências suficientes para rejeitar a hipótese nula.

Em harmonia com meus pensamentos, em setembro de 2018, um artigo foi escrito por pessoas influentes que pediam para abandonar o conceito de "significância estatística" e o paradigma de testar a hipótese nula.

Mais importante: “Sugestões como alterar o nível do limite $$p - valores por padrão, usando intervalos de confiança com ênfase em se eles contêm zero ou não, ou usando o coeficiente de Bayes junto com classificações universalmente aceitas para avaliar a força da evidência que provém de todos os problemas iguais ou similares ao uso atual$p$$$Os valores p com um nível de 0,05 ... são uma forma de alquimia estatística que faz uma falsa promessa de transformar a aleatoriedade em confiabilidade, a chamada “lavagem de incertezas” (Gelman, 2016), que começa com dados e termina com conclusões dicotômicas binárias sobre verdade ou falsidade - binária declarações de que "há um efeito" ou "não há efeito" - com base na conquista de alguns$p$$$valor p ou outro valor limite. Um passo crítico adiante será a aceitação da incerteza e a variabilidade dos efeitos (Carlin, 2016; Gelman, 2016), o reconhecimento de que podemos aprender mais (muito mais) sobre o mundo, abandonando a falsa promessa de certeza oferecida por essa dicotomização. ”$p$

Conclusões

Vimos que, embora a propriedade de simetria da relação de cointegração deva ser satisfeita teoricamente, os dados experimentais divergem dos cálculos teóricos. Uma das interpretações desse paradoxo é a baixa potência do teste de Dickey-Fuller.

Como nova metodologia para identificar pares de ativos co-integrados, foi proposto testar os resíduos de regressão obtidos pelo teste de estacionariedade de Angle-Granger usando o teste de KPSS e combinar os resultados desses testes; e combine os resultados do teste de Angle-Granger e o teste KPSS para regressão direta e reversa.

Os backtests foram conduzidos com os dados da Bolsa de Moscou de 2017. De acordo com os resultados dos backtests, o rendimento médio anual da metodologia de identificação de pares de ações cointegradas acima proposto foi de 22,72%. Assim, comparado à identificação de pares de ações co-integrados pelo teste de Angle-Granger, foi possível aumentar o rendimento médio anual em 9,21%.

Uma interpretação alternativa do paradoxo é não aceitar a hipótese nula, confirmada pela análise estatística, sobre fé. O paradigma de teste de hipótese nula e a dicotomia oferecida por esse paradigma nos dão uma falsa sensação de conhecimento do mercado.

Quando eu comecei minha pesquisa, pareceu-me que você pode pegar o mercado, colocá-lo no "moedor de carne" dos testes estatísticos e obter linhas saborosas filtradas na saída. Infelizmente, agora vejo que esse conceito de força bruta estatística não funcionará.

Se existe ou não cointegração no mercado - para mim essa questão permanece em aberto. Ainda tenho grandes perguntas para os fundadores dessa teoria. Eu costumava ter alguma ansiedade no Ocidente e aqueles cientistas que desenvolveram matemática financeira em um momento em que a econometria era considerada uma burguesia corrupta na União Soviética. Pareceu-me que estávamos muito atrasados, e em algum lugar da Europa e da América estavam sentados os deuses das finanças, que conheciam o sagrado graal da verdade.

Agora entendo que os cientistas europeus e americanos não são muito diferentes dos nossos, a única diferença está na escala do charlatanismo. Nossos cientistas estão sentados em um castelo de marfim, escrevem algumas besteiras e recebem doações de 500 mil rublos. No Ocidente, aproximadamente os mesmos cientistas estão sentados no mesmo castelo de marfim, escrevem sobre o mesmo absurdo e recebem "nobel" e doações no valor de 500 mil dólares por isso. Essa é toda a diferença.

No momento, não tenho uma visão clara do assunto de minha pesquisa. É errado dizer que “todos os fundos de hedge usam negociação de pares” porque a maioria dos fundos de hedge também vai à falência.

Infelizmente, você sempre precisa pensar e tomar decisões com sua própria cabeça, especialmente quando arriscamos dinheiro.