A programação dinâmica tem uma reputação pelo método que você estuda na universidade e só se lembra durante as entrevistas. Mas, de fato, o método é aplicável em muitas situações. De fato, esta é uma técnica para resolver efetivamente problemas que podem ser divididos em muitas subtarefas altamente repetitivas .

No artigo, mostrarei uma aplicação real interessante da programação dinâmica - a tarefa de escultura de costura. A tarefa e a metodologia são descritas em detalhes no trabalho de Avidan e Shamir “Cortando costuras para redimensionar imagens com base no conteúdo” (artigo em domínio público).

Este é um de uma série de artigos sobre programação dinâmica. Se você deseja aprimorar os métodos, consulte a introdução ilustrada à programação dinâmica .

Redimensionar imagem com base no conteúdo

Para resolver um problema real usando a programação dinâmica, você precisa formulá-lo corretamente. Esta seção descreve as predefinições necessárias para a tarefa selecionada.

Os autores do artigo original descrevem o redimensionamento da imagem orientada ao conteúdo, ou seja, alterando a largura ou a altura da imagem com base no conteúdo. Veja o trabalho original para obter detalhes, e eu ofereço uma breve visão geral. Suponha que você queira redimensionar a foto de um surfista:


Vista superior de um surfista no meio de um oceano calmo, com ondas turbulentas à direita. Foto: Kiril Dobrev no Pixabay

Conforme descrito em detalhes no artigo, existem várias maneiras de reduzir a largura da imagem: são cortes e redimensionamentos padrão, com suas desvantagens inerentes, além de remover colunas de pixels do meio. Como você pode imaginar, isso deixa uma costura visível na foto, onde a imagem à esquerda e à direita não coincidem. E dessa maneira, você pode excluir apenas uma quantidade limitada de imagem.


Uma tentativa de reduzir a largura cortando o lado esquerdo e cortando o bloco no meio. Este último deixa uma costura visível.

Avidan e Shamir no artigo descrevem a nova técnica de "escultura de costura". Primeiro, identifica áreas de “baixa energia” menos importantes e depois calcula as “costuras” de baixa energia que passam pela imagem. No caso de reduzir a largura da imagem, uma costura vertical é determinada da parte superior da imagem para a parte inferior, que em cada linha é deslocada para a esquerda ou direita por não mais que um pixel.

Na foto do surfista, a menor costura de energia percorre o meio da imagem, onde a água é a mais silenciosa. Isso é consistente com a nossa intuição.


A costura de menor energia encontrada na imagem do surfista é mostrada com uma linha vermelha de cinco pixels de largura para visibilidade, embora, na verdade, a costura tenha apenas um pixel de largura.

Depois de determinar a costura com menos energia e removê-la, reduzimos a largura da imagem em um pixel. Repetir esse processo repetidas vezes reduz significativamente a largura da foto inteira.


Imagem de surfista após redução de largura em 1024 pixels

Novamente, o algoritmo removeu logicamente a água parada no meio e no lado esquerdo da foto. Mas, diferentemente do corte, a textura da água à esquerda é preservada e não há transições nítidas. É verdade que você pode encontrar algumas transições imperfeitas no centro, mas basicamente o resultado parece natural.

Definição de energia da imagem

A mágica é encontrar a costura de energia mais baixa. Para fazer isso, primeiro atribuímos energia a cada pixel da imagem. Em seguida, usamos a programação dinâmica para encontrar o caminho através da imagem com menos energia - esse algoritmo será discutido em detalhes na próxima seção. Primeiro, vamos ver como atribuir valores de energia aos pixels.

O artigo científico discute várias funções energéticas e suas diferenças. Não vamos complicar isso e tomar uma função que simplesmente captura a quantidade de mudança de cor em torno de cada pixel. Para completar, descreverei a função de energia com mais detalhes, caso você queira implementá-la, mas isso é apenas uma predefinição para cálculos de programação dinâmica subsequentes.


À esquerda, há três pixels do escuro para o claro. A diferença entre o primeiro e o último é grande. Três pixels escuros à direita, com uma pequena diferença na intensidade da cor

Para calcular a energia de um pixel específico, observe os pixels à esquerda e à direita dele. Em termos de componentes, calculamos o quadrado da distância entre eles, ou seja, o quadrado da diferença entre os componentes vermelho, verde e azul e os adicionamos. Fazemos o mesmo para pixels acima e abaixo do centro. Por fim, some as distâncias horizontais e verticais.

$$

$$| \ Delta x | ^ 2 = (\ Delta r_x) ^ 2 + (\ Delta g_x) ^ 2 + (\ Delta b_x) ^ 2$$

$$

$$| \ Delta y | ^ 2 = (\ Delta r_y) ^ 2 + (\ Delta g_y) ^ 2 + (\ Delta b_y) ^ 2$$

$$

$$e (x, y) = | \ Delta x | ^ 2 + | \ Delta y | ^ 2$$

A única ressalva - digamos, se um pixel estiver na borda esquerda, não haverá vizinho à esquerda. Nesse caso, comparamos apenas com o pixel certo. Verificações semelhantes são realizadas para pixels nas bordas superior, direita e inferior.

A função de energia é ótima se os pixels vizinhos tiverem cores muito diferentes e pequena se forem semelhantes.


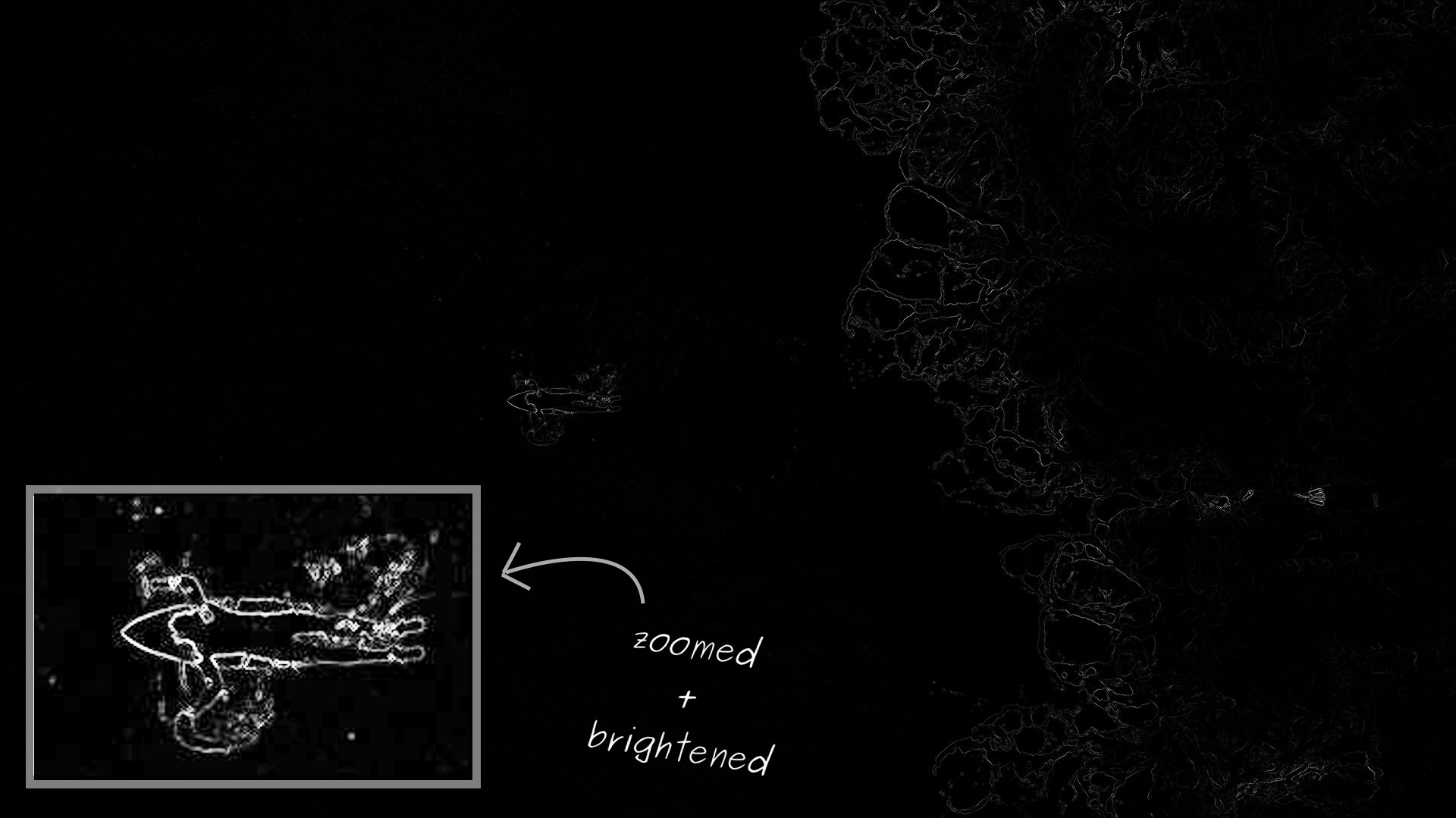A energia de cada pixel na foto de um surfista: quanto mais leve, mais alto ele é. Como esperado, o surfista tem a maior energia nas ondas médias e turbulentas à direita

A função de energia funciona bem em uma foto de surfista. No entanto, é preciso uma gama muito ampla de valores. Portanto, ao renderizar, parece que na maioria das fotos os pixels têm energia zero. De fato, existem simplesmente valores muito baixos em comparação com as regiões com maior energia. Para simplificar a visualização, ampliei o surfista e destaquei esta área.

Procure costuras de baixa energia com programação dinâmica

Ao calcular a energia de cada pixel, podemos encontrar a costura com a menor energia, de cima para baixo na imagem. A mesma análise se aplica às costuras horizontais para reduzir a altura da imagem original. No entanto, focaremos nos verticais.

Vamos começar com a definição:

• Uma costura é uma sequência de pixels, um pixel por linha. O requisito é que, entre duas linhas consecutivas, a coordenada $$$x$muda em não mais que um pixel. Isso preserva a sequência de costura.
  
• A costura com a menor energia é aquela cuja energia total em todos os pixels da costura é minimizada.

É importante notar que a junta com a menor energia não passa necessariamente por todos os pixels com a menor energia. A energia total de todos, não os pixels individuais, é levada em consideração.


A abordagem gananciosa não funciona. Escolhendo um pixel de baixa energia em um estágio inicial, ficamos presos na região de alta energia da imagem (caminho vermelho à direita)

Como você pode ver, não é possível selecionar o pixel de menor energia na próxima linha.

Dividimos o problema em subtarefas

O problema com a abordagem gananciosa é que, ao decidir sobre o próximo passo, não levamos em consideração o restante da costura à frente. Não podemos olhar para o futuro, mas somos capazes de levar em consideração tudo o que já sabemos até agora.

Vamos virar a tarefa de cabeça para baixo. Em vez de escolher entre vários pixels para continuar uma costura, escolheremos entre várias costuras para ir para um pixel . O que precisamos fazer é pegar cada pixel e escolher entre os pixels na linha acima, de onde a costura pode vir. Se cada um dos pixels na linha acima codifica o caminho percorrido até este ponto, então estamos essencialmente olhando para o histórico completo até esse ponto.


Para cada pixel, estudamos três pixels na linha acima. Escolha fundamental - qual das costuras deve continuar?

Isso pressupõe uma subtarefa para cada pixel na imagem. A subtarefa deve encontrar o melhor caminho para um pixel específico, por isso é uma boa ideia associar a cada pixel a energia da costura de baixa energia que termina nesse pixel .

Ao contrário da abordagem gananciosa, a abordagem acima tenta essencialmente todos os caminhos possíveis através da imagem. É só que, ao verificar todos os caminhos possíveis, as mesmas subtarefas são resolvidas repetidamente, o que torna essa abordagem uma opção ideal para programação dinâmica.

Definição de uma relação de recorrência

Como sempre, agora precisamos formalizar a ideia em uma relação recursiva. Há uma subtarefa correspondente a cada pixel na imagem original, portanto, as entradas para a nossa relação de recorrência podem ser apenas coordenadas $$$x$e $$$y$deste pixel. Isso fornece entradas inteiras, facilitando a organização de subtarefas, bem como a capacidade de armazenar valores calculados anteriormente em uma matriz bidimensional.

Definir uma função $$$M (x, y)$, que representa a energia da costura vertical com menos energia. Começa na parte superior da imagem e termina em um pixel $$$(x, y)$. Título $$$M$selecionado como no artigo científico original.

Primeiro, você precisa de uma versão básica. Todas as costuras que terminam na linha superior têm apenas um pixel. Assim, uma costura com energia mínima é apenas um pixel com energia mínima:

$$

$$M (x, 0) = e (x, 0)$$

Para pixels nas linhas restantes, observe os pixels na parte superior. Como a costura deve ser contínua, levamos em conta apenas três pixels localizados no canto superior esquerdo, superior e superior direito. Nelas, selecionamos a costura com a menor energia, que termina em um desses pixels, e adicionamos a energia do pixel atual:

$$

$$M (x, y) = e (x, y) + \ min \ begin {cases} M (x - 1, y - 1) \\ M (x, y - 1) \\ M (x + 1, y - 1) \ end {cases}$$

Como uma situação limítrofe, considere o caso quando o pixel atual estiver na borda esquerda ou direita da imagem. Nestes casos, omitimos $$$M (x-1, y-1)$para pixels na borda esquerda ou $$$M (x + 1, y-1)$na borda direita.

Finalmente, você precisa extrair a energia da costura de baixa energia, que cobre toda a altura da imagem. Isso significa que olhamos para a linha inferior da imagem e selecionamos a costura de menor energia que termina em um desses pixels. Para foto ampla $$$W$e alto $$$H$pixels:

$$

$$\ min_ {0 \ le x <W} M (x, H - 1)$$

Portanto, temos uma relação de recorrência com todas as propriedades necessárias:

• Uma relação de recorrência possui entradas inteiras.
  
• A resposta final é fácil de extrair da relação.
  
• A proporção depende de si mesmo.

Verificação da subtarefa DAG (gráfico acíclico orientado)

Como cada subtarefa $$$M (x, y)$corresponde a um pixel da imagem original, o gráfico de dependência é muito fácil de visualizar. Basta colocá-los em uma grade bidimensional, como na imagem original!


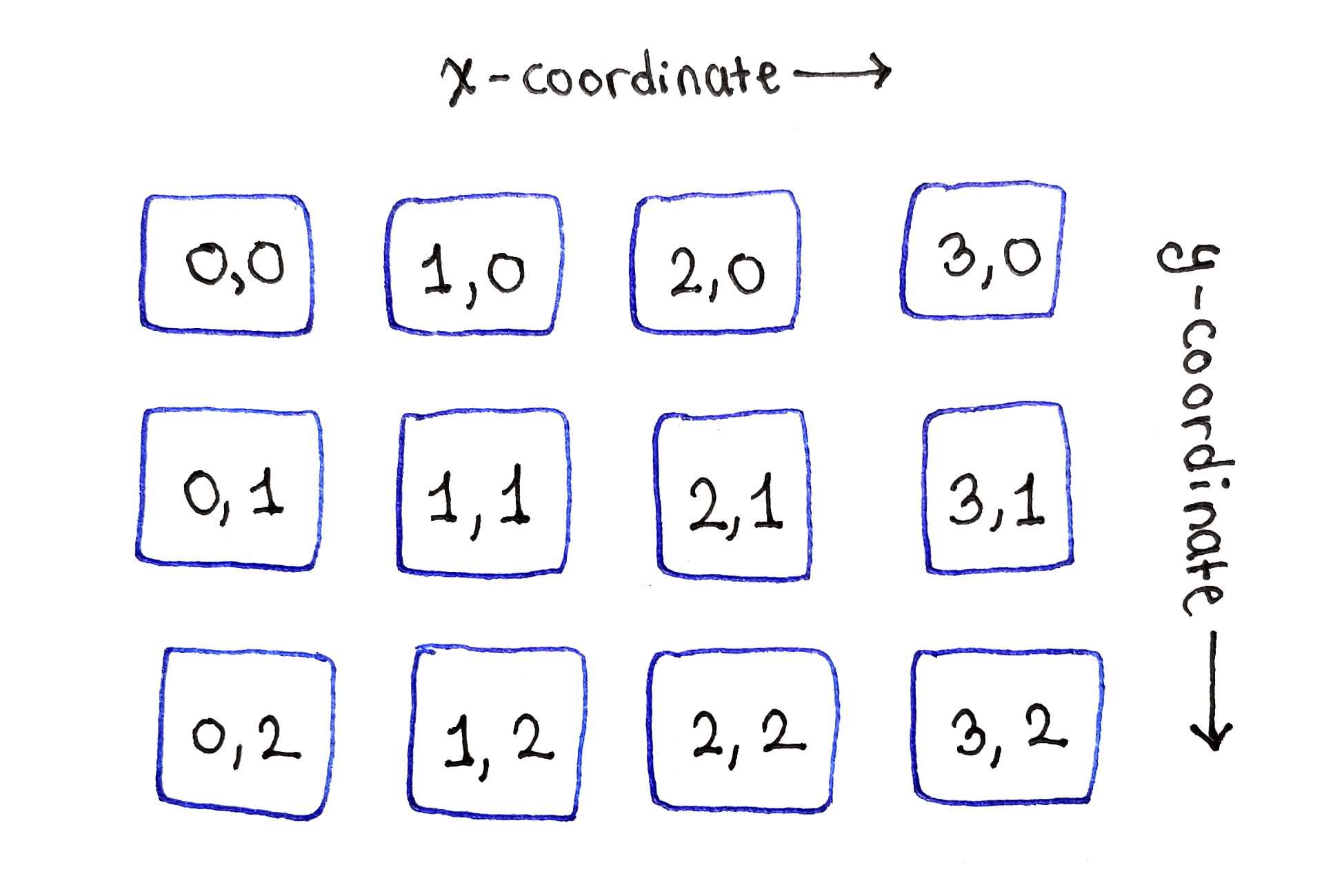As subtarefas estão localizadas em uma grade bidimensional, como os pixels na imagem original

Como segue no cenário base da relação de recorrência, a linha superior das subtarefas pode ser inicializada com os valores de energia de pixels individuais.


A linha superior é independente de outras subtarefas. Observe a ausência de setas na linha superior das células

Na segunda linha, as dependências começam a aparecer. Em primeiro lugar, na célula mais à esquerda da segunda linha, estamos diante de uma situação de fronteira. Como não há células à esquerda, a célula $$$(1,0)$depende apenas das células localizadas diretamente acima e no canto superior direito. O mesmo acontecerá mais tarde com a célula mais à esquerda na terceira linha.


As subtarefas na borda esquerda dependem apenas de duas subtarefas acima delas

Na segunda célula da segunda linha (1,1), vemos a manifestação mais típica da relação de recorrência. Essa célula depende de três células: superior esquerda, logo acima e superior direita. Essa estrutura de dependência se aplica a todas as células "intermediárias" na segunda e nas linhas subseqüentes.


As subtarefas entre as bordas esquerda e direita dependem das três subtarefas na parte superior

Por fim, a célula na borda direita representa a segunda situação limítrofe. Como não há mais células à direita, isso depende apenas das células diretamente na parte superior e superior esquerda.


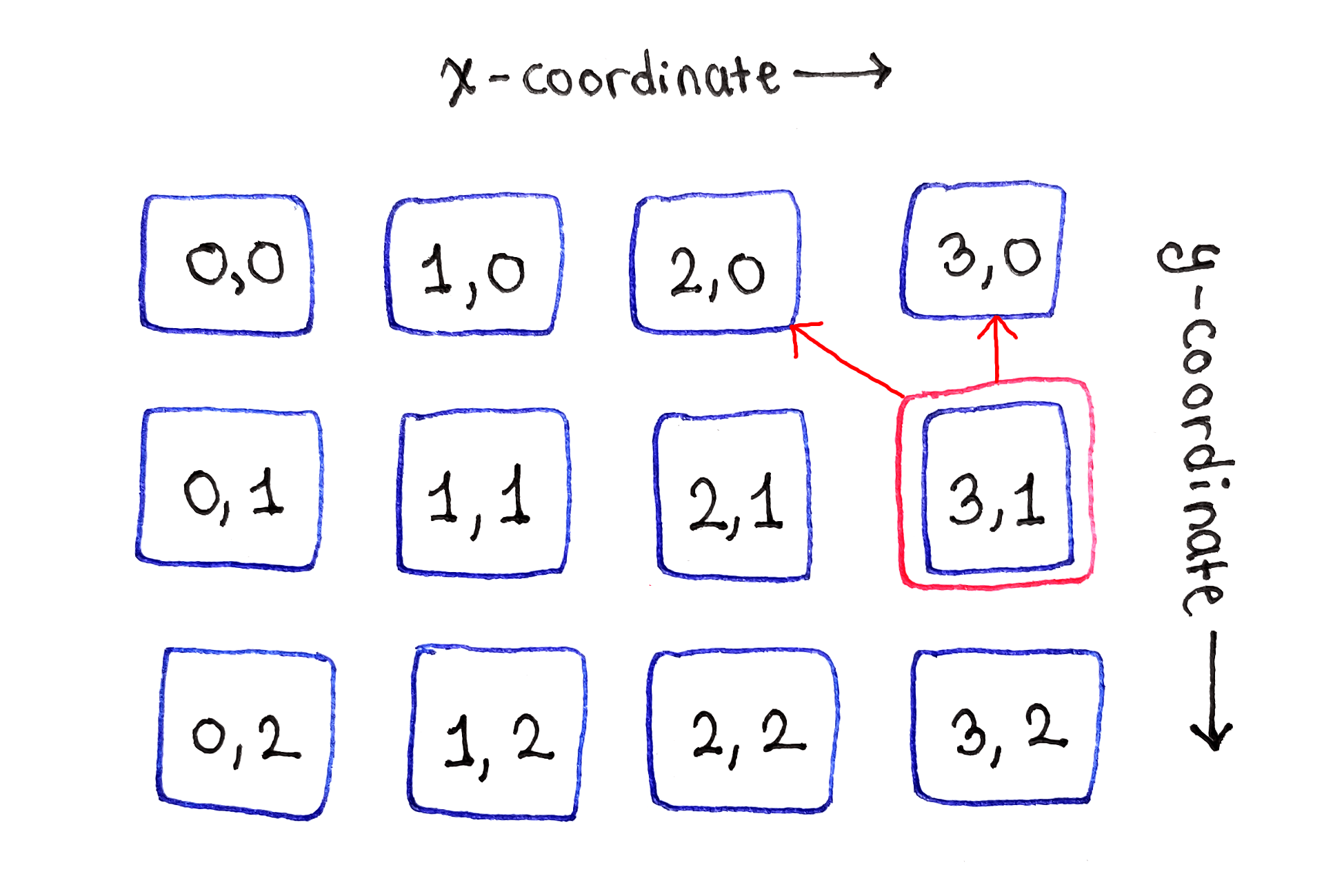As subtarefas na borda direita dependem de apenas duas células na parte superior

O processo é repetido para todas as linhas subseqüentes.


Como existem muitas setas no gráfico de dependência, esta animação mostra as dependências de cada subtarefa por vez.

Um gráfico de dependência completo assusta você com um grande número de setas, mas examiná-las uma por vez ajuda a estabelecer padrões explícitos.

Implementação de baixo para cima

Depois de realizar essa análise, obtivemos a ordem de processamento:

• Vá da parte superior da imagem para a parte inferior.
  
• Cada linha pode atuar em qualquer ordem. A escolha natural é ir da esquerda para a direita.

Como cada linha depende apenas da anterior, é necessário salvar apenas duas linhas de dados: uma para a linha anterior e outra para a linha atual. Movendo da esquerda para a direita, podemos até descartar elementos individuais da linha anterior à medida que são usados. No entanto, isso complica o algoritmo, pois ele precisa descobrir quais partes da linha anterior podem ser descartadas.

No código Python a seguir, a entrada é uma lista de linhas, em que cada linha contém uma lista de números que representam as energias de pixels individuais nessa linha. A entrada é chamada pixel_energies e pixel_energies[y][x] representa a energia do pixel em coordenadas $$$(x, y)$.

Vamos começar calculando a energia das costuras da linha superior, simplesmente copiando as energias individuais dos pixels na linha superior:

 previous_seam_energies_row = list(pixel_energies[0]) 

Em seguida, percorremos as linhas de entrada restantes, calculando as energias da costura para cada linha. A parte mais "difícil" é determinar a quais elementos da linha anterior se referir, já que não há pixels à esquerda da borda esquerda ou à direita da borda direita.

A cada iteração, uma nova lista de energias de costura para a linha atual é criada. No final da iteração, substituímos os dados da linha anterior pelos dados da linha atual para a próxima iteração. É assim que descartamos a linha anterior:

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_seam_energy = pixel_energy + \ min(previous_seam_energies_row[x_i] for x_i in x_range) seam_energies_row.append(min_seam_energy) previous_seam_energies_row = seam_energies_row 

Como resultado, previous_seam_energies_row contém a energia da costura para a linha de fundo. Encontramos o valor mínimo nesta lista - e esta é a resposta!

 min(seam_energy for seam_energy in previous_seam_energies_row) 

Você pode testar essa implementação envolvendo o código em uma função e, em seguida, chamando-o com a matriz bidimensional criada. A entrada a seguir foi escolhida para que a abordagem gananciosa falhe, com uma costura óbvia com a menor energia:

 ENERGIES = [ [9, 9, 0, 9, 9], [9, 1, 9, 8, 9], [9, 9, 9, 9, 0], [9, 9, 9, 0, 9], ] print(min_seam_energy(ENERGIES)) 

Complexidade espacial e temporal

Cada pixel na imagem original corresponde a uma subtarefa. Para cada uma das subtarefas, não há mais de três dependências, portanto, resolver cada uma delas envolve uma quantidade constante de trabalho. A última linha é realizada duas vezes. Então, para imagem ampla $$$W$e alto $$$H$a complexidade de tempo dos pixels é $$$O (L × A + L)$.

A cada momento, temos duas listas: uma para a linha anterior e outra para a atual. No primeiro $$$W$elementos eo segundo aumenta gradualmente para $$$W$. Assim, a complexidade espacial é igual a $$$O (2W)$isso é apenas $$$O (w)$.

Observe que, se realmente descartássemos os elementos de dados da linha anterior, reduziríamos a lista de elementos da linha anterior na mesma velocidade que a lista da linha atual aumenta. Assim, a complexidade espacial permanecerá $$$O (w)$. Embora a largura possa variar, isso geralmente não é tão importante.

Ponteiros de retrocesso de baixa energia

Então, descobrimos o significado da costura de baixa energia, mas o que fazer com essa informação? Afinal, de fato, não estamos preocupados com a importância da energia, mas com a própria costura! O problema é que não há como o pixel final retornar ao restante da costura.

Isso é o que eu perdi nos artigos anteriores, mas o mesmo se aplica a muitos problemas de programação dinâmica. Por exemplo, se você se lembra da tarefa de assaltante de casa , encontramos o valor máximo para a quantidade de assaltos, mas não quais casas específicas precisam ser roubadas para obter essa quantia.

Representação de ponteiros de volta

Resposta geral: armazene os ponteiros de volta . Na tarefa de cortar costuras, precisamos não apenas do valor da energia da costura em cada pixel. Você também precisa saber qual dos pixels da linha anterior levou a essa energia. Armazenando essas informações, podemos seguir os ponteiros reversos até a linha superior, obtendo as coordenadas de todos os pixels que compõem a junta com menos energia.

Primeiro, crie uma classe para armazenar energia e indicadores de retorno. A energia será usada para calcular subtarefas. Como o ponteiro para trás determina qual pixel na linha anterior forneceu a energia atual, podemos imaginá-lo simplesmente como a coordenada x.

 class SeamEnergyWithBackPointer(): def __init__(self, energy, x_coordinate_in_previous_row=None): self.energy = energy self.x_coordinate_in_previous_row = x_coordinate_in_previous_row 

O resultado do cálculo para cada subtarefa não será apenas um número, mas uma instância dessa classe.

Armazenamento de ponteiro para trás

No final, você precisa voltar ao longo de toda a altura da imagem, seguindo os sinais reversos para restaurar a costura com menos energia. Infelizmente, isso significa que você precisa armazenar ponteiros para todos os pixels da imagem, não apenas para a linha anterior.

Para isso, simplesmente salvamos o resultado completo de todas as subtarefas, embora seja tecnicamente possível abandonar as energias numéricas da costura das linhas anteriores. Os resultados são armazenados em uma matriz bidimensional, com a mesma aparência da matriz de entrada.

Vamos começar com a primeira linha, que contém apenas energias de pixels individuais. Como não há linha anterior, todos os ponteiros de trás estão ausentes, mas, por consistência, ainda armazenaremos instâncias de SeamEnergyWithBackPointers :

 seam_energies = [] # Initialize the top row of seam energies by copying over the top row of # the pixel energies. There are no back pointers in the top row. seam_energies.append([ SeamEnergyWithBackPointer(pixel_energy) for pixel_energy in pixel_energies[0] ]) 

O loop principal funciona basicamente da mesma forma que a implementação anterior, com as seguintes diferenças:

• Os dados da linha anterior contêm instâncias de SeamEnergyWithBackPointer ; portanto, ao calcular o valor da taxa de recorrência, você deve procurar a energia da costura dentro desses objetos.
  
• Salvando dados para o pixel atual, você precisa criar uma nova instância do SeamEnergyWithBackPointer . Aqui, armazenaremos a energia da costura para o pixel atual, bem como a coordenada x da linha anterior, usada para calcular a energia da costura atual.
  
• No final de cada linha, em vez de descartar os dados da linha anterior, simplesmente adicionamos os dados da linha atual a seam_energies .

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_parent_x = min( x_range, key=lambda x_i: seam_energies[y - 1][x_i].energy ) min_seam_energy = SeamEnergyWithBackPointer( pixel_energy + seam_energies[y - 1][min_parent_x].energy, min_parent_x ) seam_energies_row.append(min_seam_energy) seam_energies.append(seam_energies_row) 

Siga as indicações

Agora toda a tabela de subtarefas está preenchida e podemos restaurar a costura com menos energia. Começamos procurando a coordenada x na linha inferior, que corresponde à junta com menos energia:

 # Find the x coordinate with minimal seam energy in the bottom row. min_seam_end_x = min( range(len(seam_energies[-1])), key=lambda x: seam_energies[-1][x].energy ) 

Agora vá da parte inferior da imagem para o topo, alterando $$$y$de len(seam_energies) - 1 a zero. Em cada iteração, adicione o par atual $$$(x, y)$para a lista que representa nossa costura e defina o valor $$$x$para o objeto que SeamEnergyWithBackPointer aponta na linha atual.

 # Follow the back pointers to form a list of coordinates that form the # lowest-energy seam. seam = [] seam_point_x = min_seam_end_x for y in range(len(seam_energies) - 1, -1, -1): seam.append((seam_point_x, y)) seam_point_x = \ seam_energies[y][seam_point_x].x_coordinate_in_previous_row seam.reverse() 

Para que a costura seja construída para cima, a lista pode ser lida na ordem inversa, se você precisar de coordenadas de cima para baixo.

Complexidade espacial e temporal

A complexidade do tempo é semelhante à anterior, porque ainda precisamos processar cada pixel uma vez. Depois de olhar para a última linha e encontrar a articulação com menos energia, subimos toda a altura da imagem para restaurar a articulação. Então, para a imagem $$$W × H$complexidade de tempo é igual $$$O (L × A + L + A)$.

Quanto ao volume, ainda mantemos uma quantidade constante de dados para cada subtarefa, mas agora não descartamos nenhum dado. Então usamos volume $$$O (L × A)$.

Remoção de costura de baixa energia

Assim que a junção vertical com a menor energia for encontrada, podemos simplesmente copiar os pixels da imagem original para uma nova. Cada linha da nova imagem contém todos os pixels da linha correspondente da imagem original, com exceção do pixel da costura com a menor energia. Como excluímos um pixel em cada linha, a partir da imagem $$$W × H$então temos a imagem $$$(W - 1) × H$.

Podemos repetir esse processo recontando a função de energia na nova imagem e encontrando a costura de menor energia nela. Parece tentador encontrar mais de uma costura de baixa energia na imagem original e excluí-las todas de uma vez. O problema é que as duas costuras podem se cruzar. Quando o primeiro é excluído, o segundo se torna inválido porque um ou mais pixels estão ausentes.


Animação do processo de remoção de costura. Melhor assistir em tela cheia para ter uma visão mais clara das costuras

Cada quadro do vídeo é uma imagem em cada iteração com visualização sobreposta da costura com o mínimo de energia.

Outro exemplo

O artigo teve muitas explicações detalhadas, então vamos terminar com uma série de lindas fotos! A foto a seguir mostra uma formação rochosa no Parque Nacional Arches:


Formação rochosa com um buraco no Parque Nacional Arches. Foto: Mike Goad no Flickr

Função de energia para esta imagem:


A energia de cada pixel na foto: quanto mais leve, maior é. Preste atenção à alta energia ao redor da borda do buraco.

Como resultado do cálculo, é obtida uma costura com a menor energia. Observe que ele passa pela rocha à direita, entrando diretamente na formação rochosa, onde a parte iluminada no topo da rocha corresponde à cor do céu. Talvez você deva escolher uma função de energia melhor!


A costura de menor energia encontrada na imagem é mostrada com uma linha vermelha com cinco pixels de largura para visibilidade, embora, na verdade, a costura tenha apenas um pixel de largura.

Finalmente, a imagem do arco após o redimensionamento:


Arco após compressão em 1024 pixels

O resultado definitivamente não é perfeito: muitas bordas da montanha a partir da imagem original estão distorcidas. Uma das melhorias pode ser a implementação de uma das outras funções de energia listadas no artigo científico.

---

Embora a programação dinâmica seja geralmente discutida em teoria, é um método prático útil para resolver problemas complexos. Neste artigo, examinamos uma das aplicações da programação dinâmica: redimensionar imagens para caber no conteúdo cortando costuras.

Aplicamos os mesmos princípios de dividir uma tarefa em subtarefas menores, analisando as dependências entre essas subtarefas e resolvendo as subtarefas em uma ordem que minimiza a complexidade espacial e temporal do algoritmo. Além disso, estudamos o uso de ponteiros reversos para não apenas encontrar o valor da energia para a costura ideal, mas também para determinar as coordenadas de cada pixel que compõe esse valor. Em seguida, aplicamos essas partes a um problema real, que requer algum pré e pós-processamento para o uso realmente eficaz do algoritmo de programação dinâmica.