Na escola, quando resolvemos equações ou consideramos fórmulas, tentamos reduzi-las primeiro várias vezes, por exemplo, Z = X - (Y + X) reduzido para Z = -Y . Nos compiladores modernos, esse é um subconjunto das chamadas otimizações de olho mágico, nas quais, grosso modo, um conjunto de padrões reduzimos as expressões, substituímos as instruções pelas mais rápidas para um processador em particular, etc. Neste artigo, compilei uma coleção dessas otimizações encontradas nas fontes LLVM, GCC e .NET Core (CoreCLR).
Vamos começar com exemplos simples:
X * 1 => X -X * -Y => X * Y -(X - Y) => Y - XX * Z - Y * Z => Z * (X - Y)
verifique o último exemplo em C ++ e em C #:
int Test(int x, int y, int z) { return x * z - y * z;
e observe o assembler de Clang (LLVM), GCC, MSVC e .NET Core:

Todos os três compiladores C ++ (GCC, Clang e MSVC) reduziram uma multiplicação (vemos apenas uma instrução imul ). O C # não fez isso com o RyuJIT, mas não se apresse em censurá-lo por isso, é só que essa classe de otimizações está disponível em uma composição limitada lá. Para que você entenda, a implementação de toda a transformação InstCombine no LLVM leva mais de 30k linhas de código (+ 20k linhas no DAGCombiner.cpp); além disso, essa transformação geralmente causa uma compilação longa. A propósito, o site responsável por essa otimização está lá. O GCC possui uma DSL especial que descreve o canal de otimização ( aqui está um trecho ).
Decidi, pelo bem do artigo, tentar implementar essa otimização no C # JIT (segure minha cerveja):
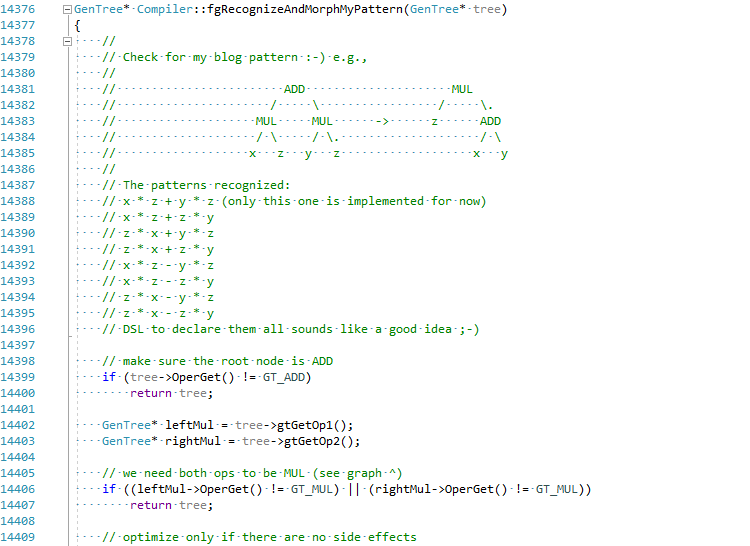
O commit completo pode ser visto aqui EgorBo / coreclr . Vamos verificar minha melhoria agora (no Visual Studio 2019 + Disasmo:
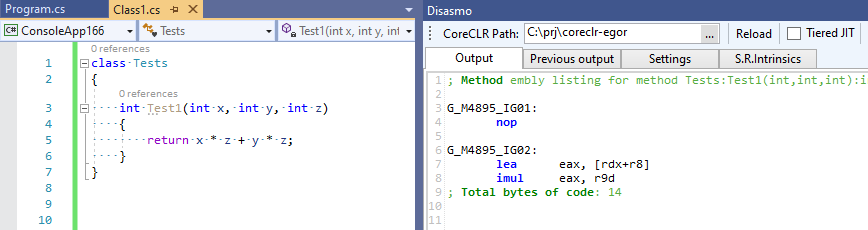
Isso funciona! lea + imul vez de imul , imul e add .
Vamos voltar ao C ++ e acompanhar essa otimização no Clang. Para fazer isso, solicite à clang que nos forneça o IR LLVM inicial via -emit-llvm -g0 e, em seguida, entregue-o ao LLVM para o otimizador, usando os parâmetros -O2 -print-before-all -print-after-all , a fim de capturar o momento exato da transformação remove a multiplicação do conjunto -O2 (tudo isso pode ser visto no maravilhoso recurso godbolt.org ):
; *** IR Dump Before Combine redundant instructions *** define dso_local i32 @_Z5Case1iii(i32, i32, i32) { %4 = mul nsw i32 %0, %2 %5 = mul nsw i32 %1, %2 %6 = sub nsw i32 %4, %5 ret i32 %6 } ; *** IR Dump After Combine redundant instructions *** define dso_local i32 @_Z5Case1iii(i32, i32, i32) { %4 = sub i32 %0, %1 %5 = mul i32 %4, %2 ret i32 %5 }
Você também pode se divertir no godbolt com as ferramentas LLVM - opt (otimizador) e llc (para compilar o LLVM IR no asm):

Voltar para os exemplos. Encontrei este exemplo muito bom no GCC.
X == C - X => false if C is odd
E é verdade: se 4 == 8 - 4 . Mas se, em vez de 8, você escrever um número ímpar, não poderá encontrar um X para que a igualdade seja cumprida:
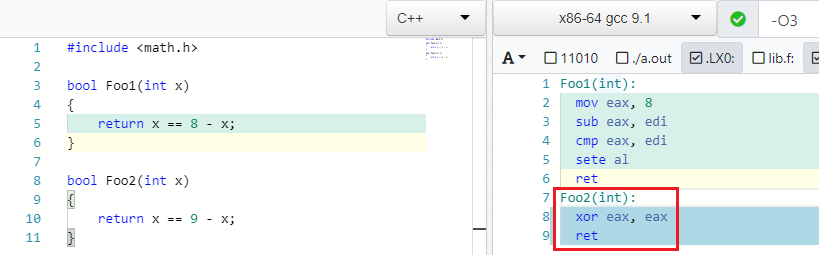
IEEE754 contra-ataca
Muitas otimizações funcionam para diferentes tipos de dados, por exemplo, byte , int , unsigned , float , double . Com o último, as coisas não são tão simples e as otimizações são tratadas pela especificação IEEE754, que ficará louca se você reduzir A - B - A para -B ou (A * B) * C reorganizá-lo para A * (B * C) t. para. operações não são associativas. Mas há um modo especial nos compiladores modernos que permite negligenciar valores de especificação e limite (NaN, + -Inf, + -0.0) nesses casos e executar otimizações com segurança - esse é o Fast Math (minha solicitação de PR para adicionar esse modo ao C # pode ser encontrada aqui )
Como você pode ver em -ffast-math não existem mais dois vsubss :
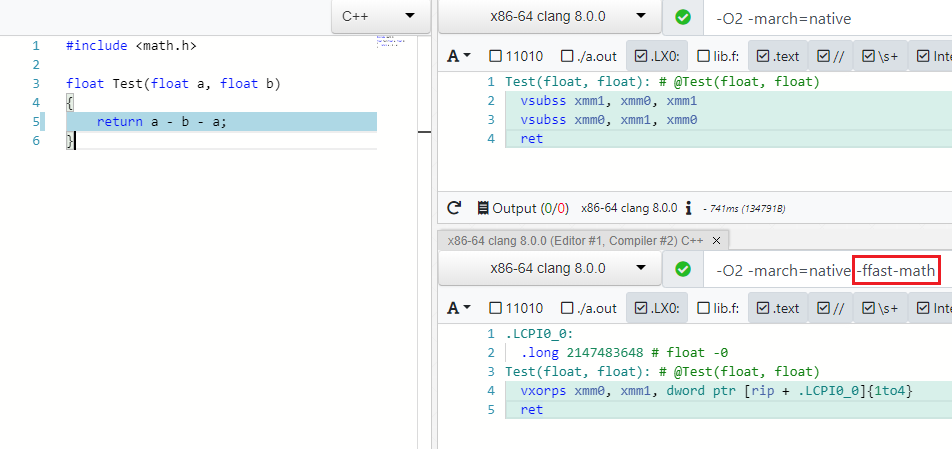
Além das expressões, os otimizadores também levam em consideração o malabarismo com funções matemáticas de math.h , por exemplo, o produto dos módulos do número X é igual ao produto do número X:
abs(X) * abs(X) => X * X
A raiz quadrada é sempre positiva:
sqrt(X) < Y => false, if Y is negative. sqrt(X) < 0 => false
Por que calcular a raiz, se é possível, no estágio de compilação, calcular o quadrado da constante à direita?
sqrt(X) > C => X > C * C

Mais operações raiz:
sqrt(X) == sqrt(Y) => X == Y sqrt(X) * sqrt(X) => X sqrt(X) * sqrt(Y) => sqrt(X * Y) logN(sqrt(X)) => 0.5*logN(X)
Um pouco mais de matemática escolar:
expN(X) * expN(Y) -> expN(X + Y)
E minha otimização favorita:
sin(X) / cos(X) => tan(X)

Muitas operações chatas e booleanas:
((a ^ b) | a) -> (a | b) (a & ~b) | (a ^ b) --> a ^ b ((a ^ b) | a) -> (a | b) (X & ~Y) |^+ (~X & Y) -> X ^ Y A - (A & B) into ~B & A X <= Y - 1 equals to X < Y A < B || A >= B -> true ... !
Otimizações de baixo nível
Existe um conjunto de otimização que, à primeira vista, não faz sentido com t.z. matemáticos, mas são mais amigáveis ao ferro.
X / 2 => X * 0.5
substitua a divisão pela multiplicação:

A operação de multiplicação de frota geralmente possui melhores características de latência / taxa de transferência do que a divisão. Por exemplo, aqui estão as opções para Intel Haswell:

No modo matemático não rápido, ele só pode ser usado se a constante for uma potência de dois.
A propósito, recentemente tentei adicionar essa otimização em C #. I.e. se, por exemplo, você precisar abrir um arquivo com um modelo 3D e reduzir todas as coordenadas em 10 vezes, * 0,1 lidará com isso 20-100% mais rápido, o que pode ser significativo.
A mesma lógica para:
X * 2 => X + X
Comparar com zero ( test ) é melhor do que comparar com unidade ( cmp ) - meu PR para obter detalhes é dotnet / coreclr # 25458 :
X >= 1 => X > 0 X < 1 => X <= 0 X <= -1 => X >= 0 X > -1 => X >= 0
E como você gosta disso:
pow(X, 0.5) => sqrt(x) pow(X, 0.25) => sqrt(sqrt(X)) pow(X, 2) => X * X ; 1 mul pow(X, 3) => X * X * X ; 2 mul

O que você acha, quantas operações de multiplicação você precisa para contar mod(X, 4) ou X * X * X * X ?
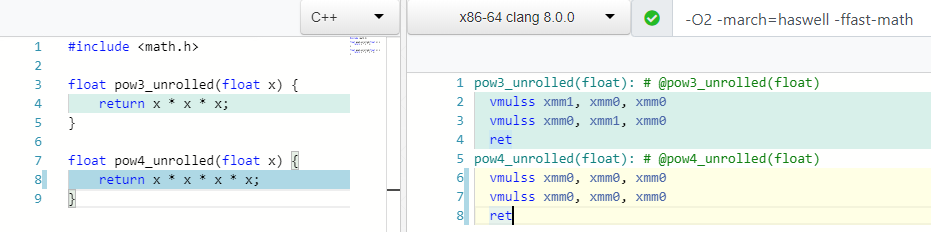
Dois! Assim como para o cálculo do 3º grau, e no caso 4, usamos apenas um registro xmm0 .
Muitos processadores oferecem suporte a uma instrução especial (FMA), que permite executar a multiplicação e adição de cada vez, mantendo a precisão durante a multiplicação:
X * Y + Z => fmadd(X, Y, Z)

Mais dois dos meus exemplos favoritos são dobrar alguns algoritmos em uma instrução (se o processador suportar):
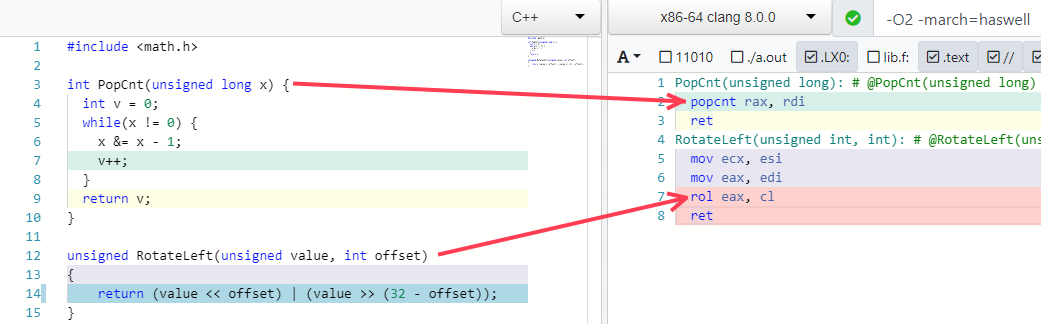
Armadilhas de otimização
Acho que todo mundo entende que você não pode se apressar e reduzir expressões por três razões:
- Você pode quebrar o código em alguns valores de limite, excesso, efeitos colaterais ocultos, etc. ... O Bugzilla LLVM contém muitos bugs do InstCombine.
- Idealmente, as otimizações devem trabalhar juntas em uma sequência específica.
- A expressão ou partes dela que você deseja reduzir podem ser usadas em outros lugares e sua redução levará à degradação do desempenho.
Vejamos um exemplo para o último parágrafo (espionado no artigo Direções futuras para otimizar compiladores ).
Imagine que temos este código:
int Foo1(int a, int b) { int na = -a; int nb = -b; return na + nb; }
precisamos fazer três operações: 0 - a , 0 - b na + nb . Mas o otimizador para nós reduz isso para dois - return -(a + b); :
define dso_local i32 @_Z4Foo1ii(i32, i32) { %3 = add i32 %0, %1 ; a + b %4 = sub i32 0, %3 ; 0 - %3 ret i32 %4 }
Agora imagine que precisamos escrever valores intermediários na e nb para variáveis globais:
int x, y; int Foo2(int a, int b) { int na = -a; int nb = -b; x = na; y = nb; return na + nb; }
O otimizador ainda encontra esse padrão e remove as operações desnecessárias (do seu ponto de vista) 0 - a e 0 - b , mas, na verdade, elas são necessárias! nós escrevemos os resultados dessas operações "desnecessárias" em variáveis globais! Isso leva a este código:
define dso_local i32 @_Z4Foo2ii(i32, i32) { %3 = sub nsw i32 0, %0 ; 0 - a %4 = sub nsw i32 0, %1 ; 0 - b store i32 %3, i32* @x, align 4, !tbaa !2 store i32 %4, i32* @y, align 4, !tbaa !2 %5 = add i32 %0, %1 ; a + b %6 = sub i32 0, %5 ; 0 - %5 ret i32 %6 }
Quatro operações matemáticas em vez de três! Nosso otimizador falhou e não estava convencido de que as expressões intermediárias que ele otimizava ainda eram necessárias para alguém. Agora, vejamos a saída do C # RuyJIT, na qual não existe essa otimização inteligente:
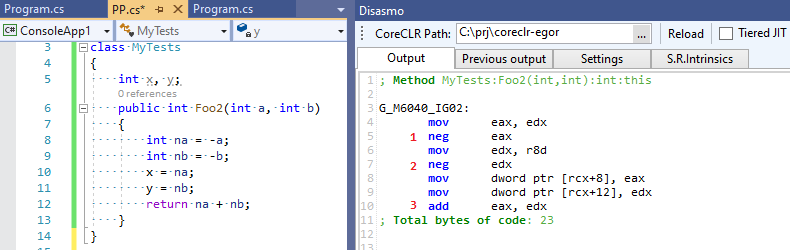
Três operações em vez de quatro - o C # acabou sendo mais rápido que o C ++ :-)!
Essas otimizações são necessárias?
Você nunca sabe como o código cuidará do compilador alinha tudo o que pode e faz dobragem constante, propagação de cópia, CSE etc. - uma imagem completamente diferente será aberta para ele. O LLVM IR e o .NET IL não estão vinculados a uma linguagem de programação específica, e você não pode ter certeza de que um PL específico / novo possa efetivamente se traduzir em IR. Bem, por que falar sobre isso, se você pode testar o desempenho do InstCombine em um aplicativo específico ;-). É improvável que isso seja uma diferença impressionante, mas quem sabe.
E o C #?
Como eu disse, as otimizações das expressões que examinamos provavelmente estão ausentes no C #. Mas quando digo C #, quero dizer que o tempo de execução mais popular é o CoreCLR e o RyuJIT. Mas, além do CoreCLR, existem outros tempos de execução, incluindo aqueles que usam o LLVM como back-end: Mono (veja meu tweet ), Unity Burst, IL2CPP (via clang) e LILLC - aqui você pode comparar com segurança os resultados C ++ com clang. Os caras do Unity até reescrevem o código C ++ interno em C # sem nenhuma perda de desempenho, prova !
Aqui estão alguns canais de otimização que podem ser encontrados no arquivo morph.cpp no código-fonte morph.cpp partir dos comentários (há claramente um pouco mais):
*(&X) => X X % 1 => 0 X / 1 => X X % Y => X - (X / Y) * Y X ^ -1 => ~x X >= 1 => X > 0 X < 1 => X <= 0 X + 1 == C2 => X == C2 - C1 ((X + C1) + C2) => (X + (C1 + C2)) ((X + C1) + (Y + C2)) => ((X + Y) + (C1 + C2))
Um pouco mais pode ser encontrado em lowering.cpp (nível baixo), mas em geral o RyuJIT obviamente perde aqui para os compiladores C ++. O RyuJIT tem prioridades ligeiramente diferentes - antes do advento da Tiering Compilation, ele precisava fornecer uma velocidade de compilação aceitável, o que faz muito bem ao contrário dos compiladores C ++ (lembre-se da passagem InstCombine de 30 linhas no LLVM e leia a postagem interessante em geral " "Lamentações C ++ modernas" ) e é muito mais útil desenvolver otimizações no campo da desvirtualização de chamadas, eliminação de boxe e alocações (a mesma alocação de pilha de objetos ) - tudo isso, obviamente, é muito mais importante do que minimizar a divisão do seno pelo cosseno na tangente.
Talvez com o advento da compilação em camadas, com o tempo, muitas novas otimizações não sejam críticas para o tempo de compilação para a camada 1 ou mesmo a camada 2. Talvez até com sua API de suplemento e DSL - você acabou de ler este artigo, nele Prathamesh Kulkarni adicionou otimização de expressão no GCC em apenas algumas linhas DSL:
(simplify (plus (mult (SIN @0) (SIN @0)) (mult (COS @0) (COS @0))) (if (flag_unsafe_math_optimizations)1. { build_one_cst (TREE_TYPE (@0))
para esta expressão de um livro de matemática ;-):
cos^2(X) + sin^2(X) equals to 1
Links úteis
- "Direções futuras para otimizar compiladores" , Nuno P. Lopes e John Regehr
- "Como o LLVM otimiza uma função" , John Regehr
- "A surpreendente inteligência dos compiladores modernos" , Daniel Lemire
- "Adicionando otimização do olho mágico ao GCC" , Prathamesh Kulkarni
- "1. C ++, C # e Unity" , Lucas Meijer
- Lamentações "modernas" em C ++ " , Aras Pranckevičius
- "Otimizações de olho mágico comprovadamente corretas com vivo" , Nuno P. Lopes, David Menendez, Santosh Nagarakatte e John Regehr