1. Introdução
Um dos primeiros radiotelescópios construídos pela American Grotto Reber em 1937. O radiotelescópio era um espelho de estanho com 9,5 m de diâmetro montado em uma moldura de madeira:

Em 1944, Reber havia compilado o primeiro mapa da distribuição de ondas de rádio espaciais na região da Via Láctea.
O desenvolvimento da radioastronomia envolveu uma série de descobertas: em 1946, foi descoberta a emissão de rádio da constelação Cygnus, em 1951 - radiação extragalática, em 1963 - quasares e em 1965, a radiação de fundo com comprimento de onda de 7,5 cm.
Em 1963, um único radiotelescópio de 300 metros foi construído em Arecibo (Porto Rico). Esta é uma tigela imóvel com um irradiador em movimento, construída em uma fenda natural do terreno.

Os radiotelescópios individuais têm uma pequena resolução angular, determinada pela fórmula:
T h e t a = f r a c l a m b d a d onde
l a m b d a - comprimento de onda
d - diâmetro do radiotelescópio.
Obviamente, para melhorar a resolução, é necessário aumentar o diâmetro da antena, o que é fisicamente uma tarefa difícil. Foi possível resolvê-lo com o advento dos interferômetros de rádio.
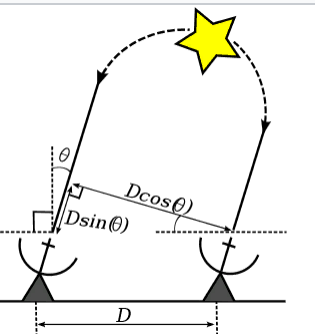
A frente de uma onda eletromagnética emitida por uma estrela distante perto da Terra pode ser considerada plana. No caso do interferômetro mais simples, constituído por duas antenas, a diferença no caminho dos raios que chegam a essas duas antenas será igual a:
D e L t um = D c d o t s i n ( t e t um ) ,
onde:
D e l t a - a diferença no caminho dos raios;
D - distância entre antenas;
T h e t uma - o ângulo entre a direção de chegada dos raios e o normal para a linha na qual as antenas estão localizadas.
At
T h e t a = 0 as ondas que chegam às duas antenas são somadas na fase. Na antifase, as ondas aparecerão pela primeira vez com:
Delta= frac lambda2, Theta=arcsin frac lambda2D ,
onde:
lambda - comprimento de onda.
O próximo máximo será em
Delta= lambda, mínimo em
Delta= frac3 lambda2 etc. É obtido um padrão de radiação de múltiplas pétalas (DN), cuja largura do lóbulo principal
lambda<<D é igual a
lambda/D . A largura do lobo principal determina a resolução angular máxima do interferômetro de rádio, é aproximadamente igual à largura do lobo.
A interferometria por rádio de base ultra longa (VLBI) é um tipo de interferometria usada na radioastronomia, na qual os elementos receptores do interferômetro (telescópios) estão localizados não mais próximos do que as distâncias continentais.
O método VLBI permite combinar as observações feitas por vários telescópios e simular um telescópio cujas dimensões são iguais à distância máxima entre os telescópios originais. A resolução angular do VLBI é dezenas de milhares de vezes maior que a resolução dos melhores instrumentos ópticos.
O estado atual das redes VLBI
Hoje, várias redes VLBI estão ouvindo espaço:
- European –EVN (Rede Europeia VLBI), composta por mais de 20 radiotelescópios;
- American –VLBA (Very Long Baseline Array), que inclui dez telescópios com um diâmetro de 25 metros cada;
- Japonês - JVN (Rede japonesa VLBI) consiste em dez antenas localizadas no Japão, incluindo quatro antenas astrométricas (projeto VERA - VLBI Exploration of Radio Astrometry);
- Australiano - LBA (Long Baseline Array);
- Chinês - CVN (rede chinesa VLBI), composto por quatro antenas;
- Coreia do Sul - KVN (Korean VLBI Network), que inclui três radiotelescópios de 21 metros;
- O russo - baseado no complexo permanente de rádio interferometria - "Kvazar-KVO" com radiotelescópios de diâmetro de 32 m, equipado com crioradiômetros altamente sensíveis no comprimento de onda de 1,35 cm a 21 cm. O comprimento das bases - o diâmetro efetivo do "espelho" sintetizado - é de cerca de 4400 km na direção leste-oeste (veja a figura).
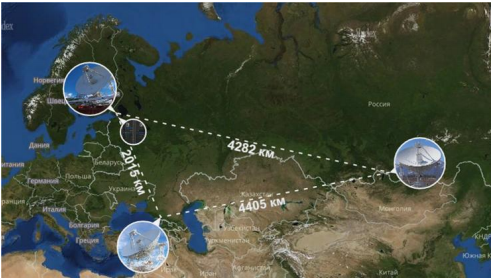
No complexo VLBI "Kvazar-KVO", os padrões de hidrogênio são usados como fonte de frequência de referência para todas as transformações de frequência, que usam a transição entre os níveis da estrutura hiperfina do estado fundamental de um átomo de hidrogênio com uma frequência de 1420,405 MHz, correspondendo a 21 cm em radioastronomia.
Tarefas resolvidas por meio do VLBI
- Astrofísica A construção de imagens de rádio de objetos do espaço natural (quasares e outros objetos) é realizada com uma resolução de décimos e centésimos de mas (milissegundos de arco).
- Estudos astrométricos. Construção de sistemas de tempo de coordenadas. Os objetos de pesquisa são fontes de rádio de tamanhos angulares extremamente pequenos, incluindo fontes de rádio quasistelares e núcleos de galáxias de rádio, que, devido à sua grande distância, são objetos quase ideais para criar uma rede de objetos estacionários de apoio.
- Pesquisa sobre mecânica celeste e a dinâmica do sistema solar, navegação espacial. A instalação de um farol nas superfícies dos planetas e o rastreamento dos faróis das estações automáticas interplanetárias possibilita o uso do método VLBI para estudar parâmetros como o movimento orbital do planeta, a direção dos eixos de rotação e sua precessão, a dinâmica do sistema planeta-satélite. Para a Lua, o problema muito importante de determinar a libração física e determinar a dinâmica dos sistemas Lua-Terra também está sendo resolvido.
Navegação no espaço usando VLBI
- Monitorando os movimentos dos astronautas na superfície lunar em 1971. Eles se moveram com a ajuda do rover lunar Rover. A precisão de determinar sua posição em relação ao módulo lunar atingiu 20 cm e dependia principalmente da libração da lua (Libration - oscilações periódicas pendulares do tipo pêndulo da lua em relação ao seu centro de massa);
- Suporte de navegação para a entrega e descarga de sondas de aeróstato de veículos voadores na atmosfera de Vênus (projeto VEGA). A distância para Vênus é superior a 100 milhões de km, a potência do transmissor é de apenas 1 Watt. Os lançamentos do VEGA-1/2 ocorreram em dezembro de 1984. Os balões foram lançados na atmosfera de Vênus em 11 e 15 de junho de 1985. A observação foi realizada por 46 horas.
Diagrama estrutural de uma rede VLBI simplificada
Com base em uma rede VLBI real, usando o software Python, modelamos um sistema VLBI simplificado na forma de modelos separados para cada unidade ou processo. Este conjunto de modelos será suficiente para observar os processos básicos. O diagrama estrutural de uma rede VLBI simplificada é apresentado na figura:
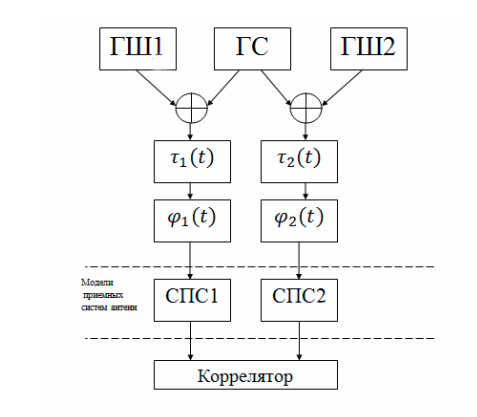
O sistema inclui os seguintes componentes:
- sinal modulado em fase útil do gerador (HS);
- geradores de ruído (GSh1, GSh2). O sistema possui dois radiotelescópios (antenas receptoras) que possuem seu próprio ruído. Além disso, existem ruídos da atmosfera e outras fontes naturais e artificiais de emissão de rádio;
- uma unidade de atraso de tempo simulando um atraso de variação linear devido à rotação da Terra;
- deslocador de fase simulando o efeito Doppler;
- sistema de conversão de sinal (SPS), consistindo em um oscilador local, para transferir o sinal para baixo em frequência, e um filtro passa-banda;
- Correlacionador de FX.
O circuito correlacionador é mostrado na figura a seguir:
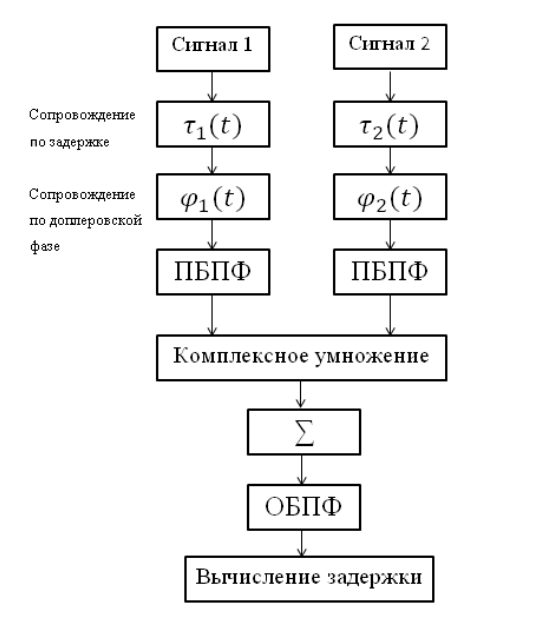
O circuito correlacionador fornecido, que inclui os seguintes blocos:
- transformada rápida direta de Fourier (PBPF) e transformada inversa de Fourier (OBPF);
- compensar o atraso introduzido anteriormente;
- efeito Doppler compensador;
- multiplicação complexa de dois espectros;
- somando implementações acumuladas.
Modelo de Sinal de Navegação
Os mais convenientes para medições de VLBI são os sinais de navegação da espaçonave de sistemas de navegação por satélite, como GPS e GLONASS. Um número de requisitos é imposto aos sinais de navegação:
- permite definir bem pseudo-faixa;
- transmitir informações sobre a posição do sistema de navegação;
- distinguir-se dos sinais de outros NS;
- Não interfira com outros sistemas de rádio;
- não requer equipamentos complexos para receber e transmitir.
Em uma extensão suficiente, eles estão satisfeitos com um sinal com modulação de fase binária (duas posições) - BPSK (tecla de mudança de fase binária), que na literatura russa é denominada FM-2. Essa modulação altera a fase da oscilação da portadora por π, que pode ser representada como:
S(t)=A cdotG(t) cdotcos(2 pipés),onde G (t) é a função de modulação.
Para implementar a modulação de fase, dois geradores podem ser usados, cada um dos quais forma a mesma frequência, mas com uma fase inicial diferente. A função de modulação permite expandir o espectro do sinal e medir com precisão a pseudo-faixa (a distância entre o satélite e o receptor, calculada pelo tempo de propagação do sinal sem correção para a diferença entre o relógio do satélite e o receptor).
Aqui está uma lista explicando os princípios básicos do BPSK:
Listagemfrom scipy import* from pylab import* import numpy as np import scaleogram as scg f = 2;
Temos:
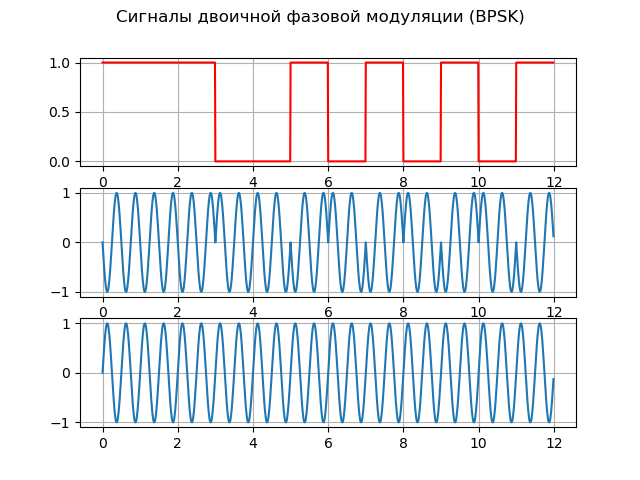
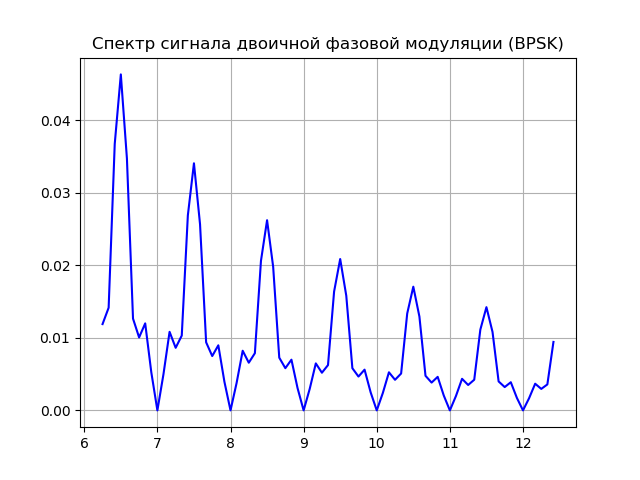
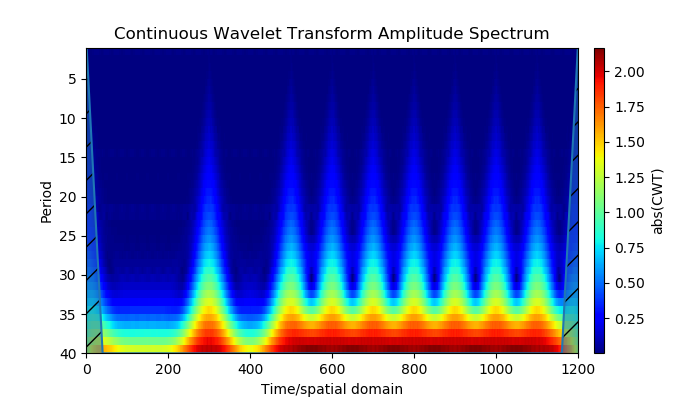
Modelo de Origem
O sinal harmônico de navegação modulado em fase de um satélite ou nave espacial tem a forma:
x=a(2 pifct+ sumsncos(2 pifnt)),onde está a frequência portadora
fc=$8, GHz
O sinal possui vários parâmetros controlados: a amplitude da enésima oscilação moduladora
sn, sua frequência
fc e a amplitude da oscilação portadora a.
Para obter uma função de correlação na qual seus lobos laterais são suprimidos o máximo possível e o pico de correlação mais estreito for atingido, variaremos os valores de frequência usando os valores de 2, 4, 8 e 16 MHz e o índice de modulação no intervalo de 0 a 2π em incrementos de π. Deixe-me fornecer uma lista do programa para essa pesquisa de parâmetros de uma função de fase modulada para o resultado final:
Temos:
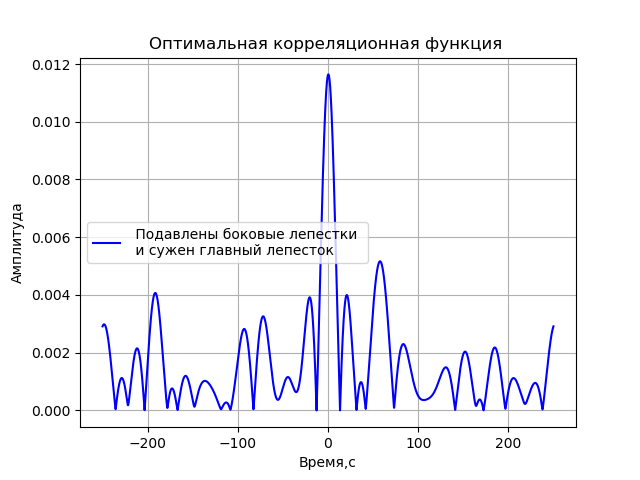
A função resultante tem a forma:
x=cos(2 pifct+2 picos(2 pi106t)+2 picos(2 pi108t)+4 picos(2 pi1016t)).(1)Além disso, esta função será usada para simular o VLBI.
Modelo de um gerador de ruído simulando interferência recebida junto com um sinal do espaço e da atmosfera da Terra
A função (1) do sinal de navegação com modulação de fase pode ser aplicada a ambos os canais do interferômetro de rádio, mas é necessário levar em consideração o atraso do sinal no segundo canal e o ruído nos dois canais, conforme mostrado na lista a seguir:
Temos:
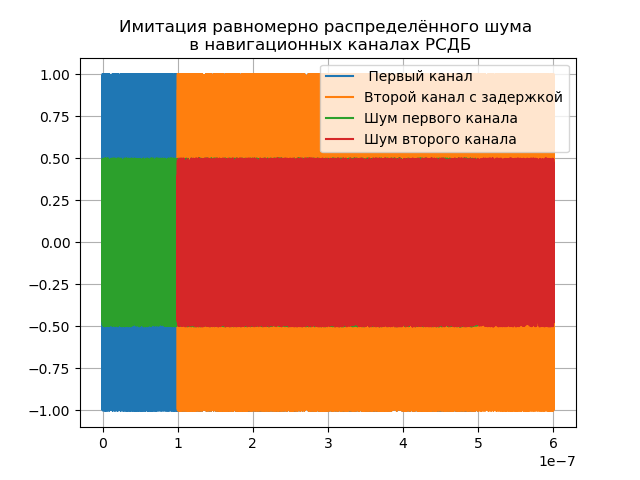
O atraso de atraso = 1e-7 é definido para demonstração, na realidade depende da base e pode atingir quatro ou mais unidades.
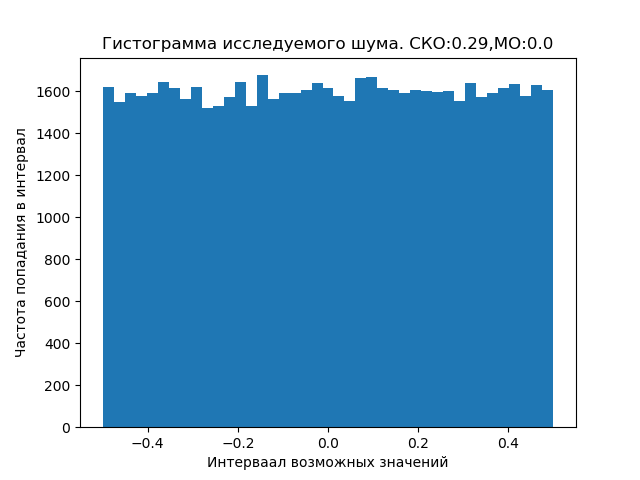
Ruídos cósmicos e próximos à Terra podem ser distribuídos de acordo com uma lei diferente do uniforme fornecido, o que requer estudos especiais.
Modelando o efeito Doppler
Devido ao fato de a Terra ter uma forma arredondada e girar em torno de seu eixo, os sinais do espaço chegam às antenas com atrasos diferentes. Por esse motivo, é necessário mudar os sinais no tempo e levar em consideração a frequência do Doppler. Consideraremos aproximadamente que o atraso varia de acordo com uma lei linear:
taux(t)=ax+bxt,(2)onde
ax=1..3 cdot10−3 ms e
bx=1..3 cdot10−6 ms A fase Doppler é encontrada como uma derivada do atraso:
fdx= fracd tau(t)dt=bx,(3)O sinal recebido deve se parecer com:
hatx=x(t− taux)ej2 pifdxt,onde x (t) é o sinal irradiado da nave espacial.
Uma demonstração do efeito Doppler é mostrada na lista a seguir:
Temos:
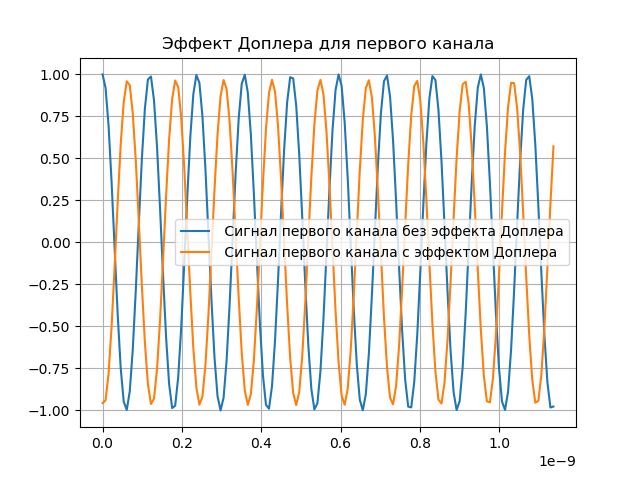
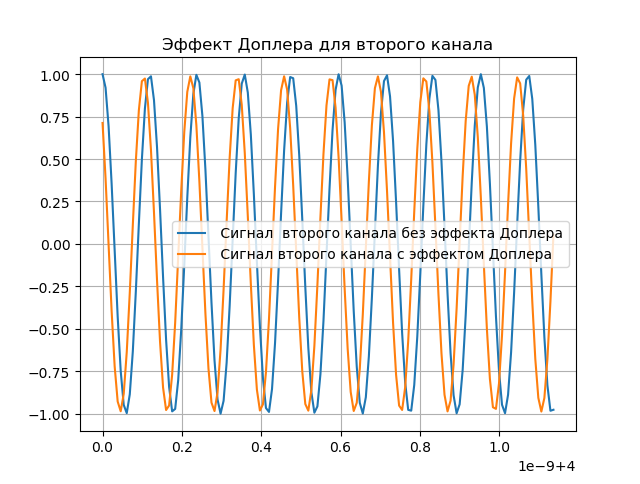
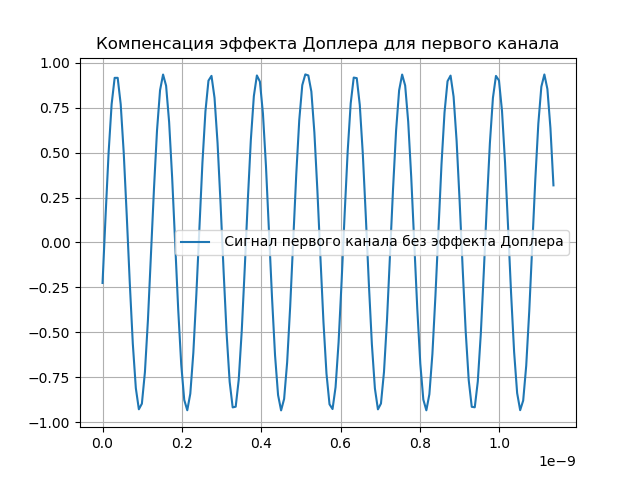
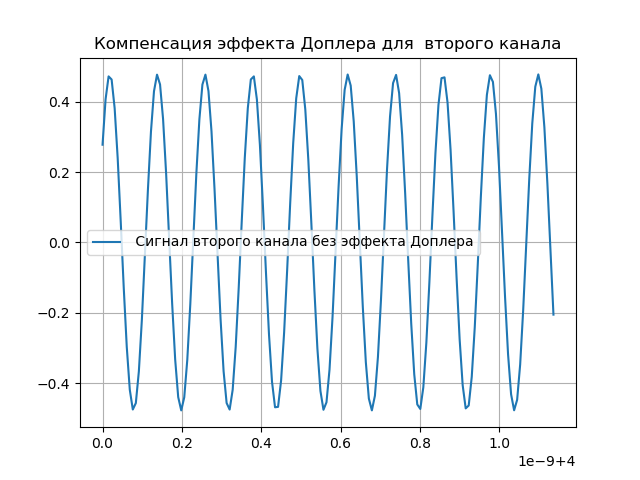
Modelagem da Compensação Doppler
Obviamente, as alterações feitas no sinal devem ser compensadas. Para esse fim, o sistema contém suporte para a fase de atraso e Doppler. Depois que o sinal passa pelo sistema de registro, é introduzido um atraso:
tauex(t)=ax+bext,(4)Considerará que o atraso é calculado com uma certa precisão, de modo que
left|aex−ax right|<30 ns
left|bex−bx right|<10 ns, ou seja, Será um pouco diferente do que ele fez com os atrasos anteriores. É claro que o atraso é introduzido com o sinal oposto ao introduzido anteriormente.
O sinal recebido será parecido com:
hatx= tilx(t+ tauex)e−j2 pifdet.(5)A compensação do efeito Doppler é mostrada na lista a seguir:
Temos:
Simulação de heteródino de sinal
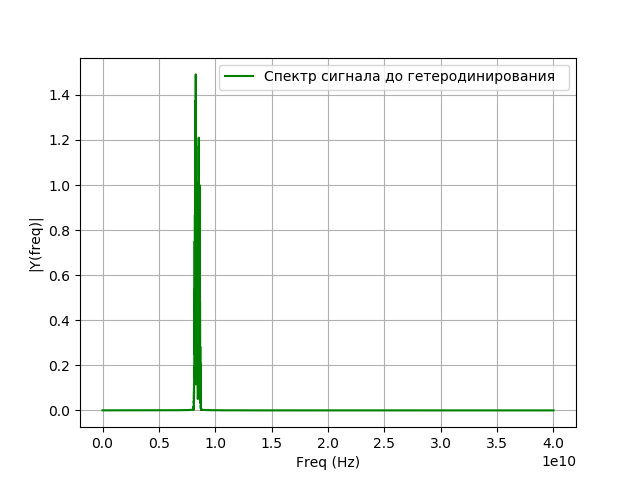
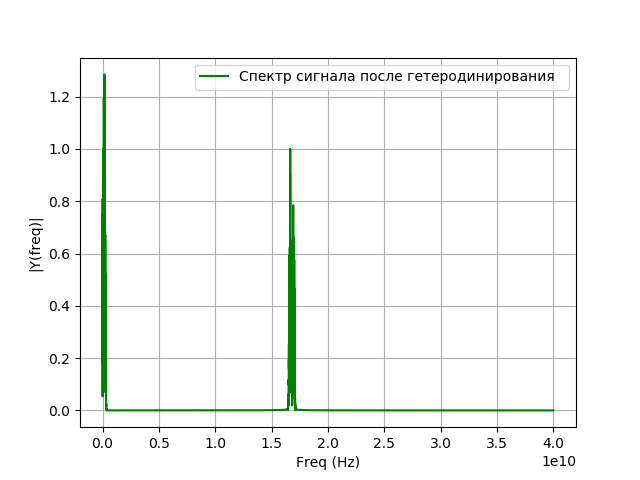
Depois que o sinal entra no sistema de registro, ocorre uma conversão de frequência, também chamada de heterodinâmica. Esta é uma transformação não linear em que dos sinais de duas frequências diferentes
f1 e
f2 o sinal de frequência de diferença é destacado -
f= esquerda|f1−f2 direita. A frequência do sinal do oscilador local será igual à diferença entre a frequência do sinal investigado e a frequência que você deseja obter após a transferência. A heterodinâmica é realizada usando um gerador auxiliar de oscilações harmônicas - um oscilador local e um elemento não linear. Matematicamente, heterodinâmica é a multiplicação de um sinal por um expoente:
xg= hatxej2 pifgt,(6)onde
fg - sinal do oscilador local.
Programa para heterodinâmica:
Temos:
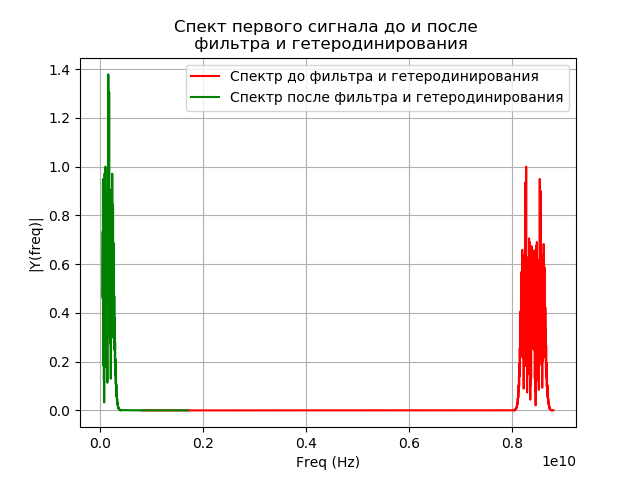
Modelagem de filtragem de sinal após heterodinâmica
Após a heterodinâmica, o sinal entra no filtro passa-banda. Filtro de banda passante (PP)
fpass=32 MHz A resposta de impulso do filtro é calculada pelo método da janela usando a função de biblioteca signal.firwin. Para obter um sinal na saída do filtro, é realizada a convolução do filtro e o sinal no domínio do tempo. A convolução integral para o nosso caso assume a forma:
checkx(t)= int+ infty− inftyxg(t)h(t−t′)dt,(7)onde h (t) é a resposta ao impulso do filtro.
A convolução é encontrada usando a função de biblioteca signal.convolve. O sinal registrado, levando em consideração a heterodinâmica e a filtragem, é apresentado na forma de uma fórmula
checkx(t)=( hatx(t)e−j2 pifgt)∗honde a convolução é indicada por *.
Programa para modelagem de filtração:
Temos:
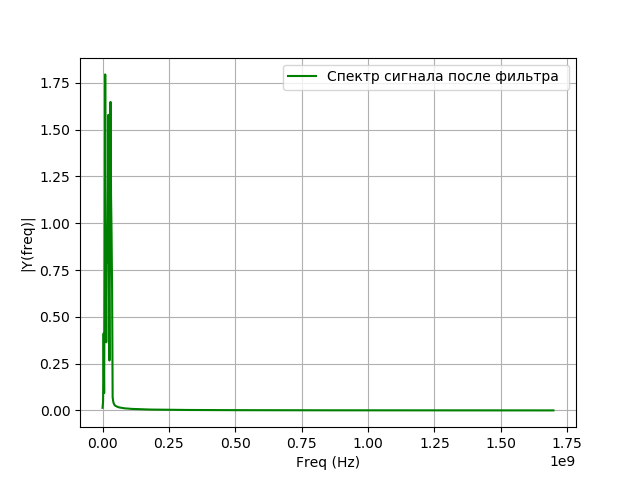
Os conversores de sinais digitais para VLBI usam principalmente filtros com resposta de impulso finito (FIR), pois possuem várias vantagens em comparação com filtros com resposta de impulso infinito (IIR):
- Os filtros FIR podem ter uma resposta de fase estritamente linear no caso de simetria da resposta ao impulso (IM). Isso significa que, usando esse filtro, é possível evitar distorções de fase, o que é especialmente importante para a interferometria de rádio. Os filtros com uma resposta de impulso infinito (IIR) não têm as propriedades de simetria deles e não podem ter uma resposta de fase linear.
- Os filtros FIR não são recursivos, o que significa que eles são sempre estáveis. A estabilidade dos filtros IIR nem sempre pode ser garantida.
- As consequências práticas do uso de um número limitado de bits para implementar filtros são significativamente menos significativas para os filtros FIR.
Na lista acima, o modelo do filtro passa-banda FIR é implementado usando o método window, a ordem do filtro foi selecionada para que o formato da resposta de frequência do filtro fosse quase retangular. O número de coeficientes do filtro simulado é n = 100001, ou seja, a ordem do filtro é P = 100000.
Programa para construir a resposta de frequência e resposta de fase do filtro FIR obtido:
Temos:

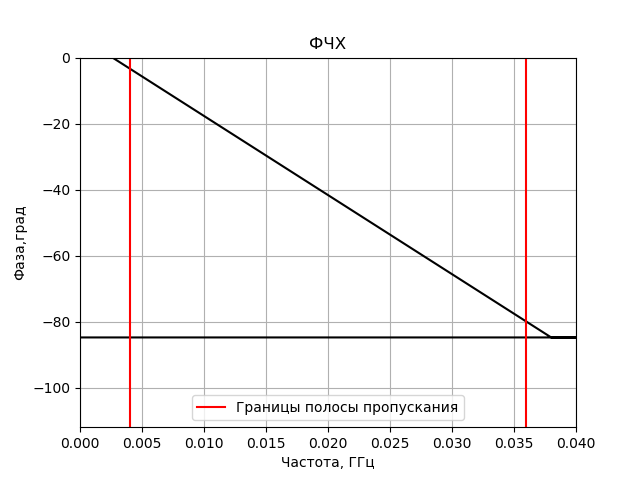
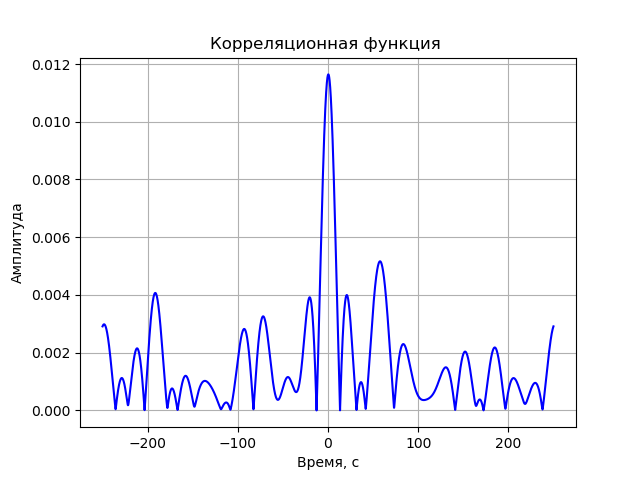
Modelo de correlação FX
A seguir, cada sinal passa por uma rápida transformação de Fourier (FFT). A FFT é implementada usando a função de biblioteca fft do scipy.fftpack. Os espectros resultantes são conjugados complexos multiplicados:
S(j omega)=S1(j omega)∗S2(j omega)=(a1+jb1)∗(a2−jb2)=a1a2+b1b2+j(b1a2−a1b2)A última ação é o inverso da FFT. Como a amplitude da função de correlação é de interesse, o sinal resultante deve ser convertido pela fórmula:
A= sqrtre2+im2O programa para a função de correlação sem levar em conta distorções do sistema de registro:
Temos:
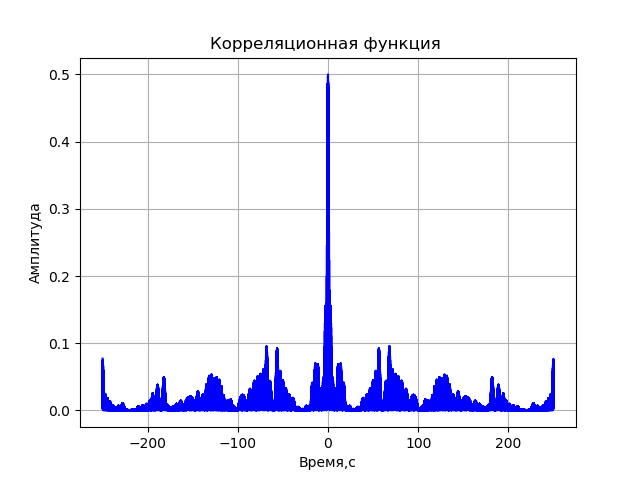
Lista completa do modelo de computador do VLBI:
Temos:
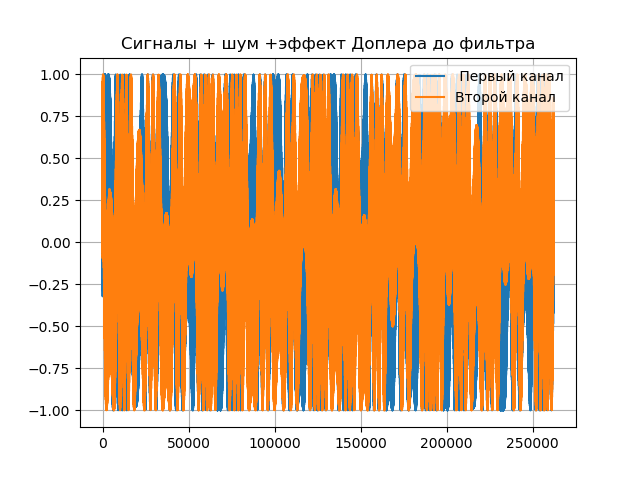

Conclusões
- É apresentada uma breve história do desenvolvimento da radioastronomia.
- O estado atual das redes VLBI é analisado.
- Os problemas resolvidos por meio de redes VLBI são considerados.
- As ferramentas Python construíram um modelo de sinais de navegação com modulação de fase binária (duas posições) - BPSK (tecla de mudança de fase binária). O modelo usa análise wavelet de modulação de fase.
- Foi obtido um modelo de fontes de sinal, que permite determinar os parâmetros de modulação que fornecem a função de correlação ideal de acordo com o critério para suprimir os lobos laterais e a amplitude máxima do lobo central.
- É obtido um modelo de rede VLBI simplificada, levando em consideração o ruído e o efeito Doppler. Os recursos de filtragem usando um filtro com uma resposta de impulso finito são considerados.
- Após um breve resumo da teoria, todos os modelos estão equipados com programas de demonstração que permitem rastrear a influência dos parâmetros do modelo.