Continuamos a falar sobre a conferência sobre estatística e aprendizado de máquina AISTATS 2019. Neste post, analisaremos artigos sobre modelos profundos de conjuntos de árvores, misturaremos a regularização para dados altamente esparsos e uma aproximação com tempo eficiente da validação cruzada.

Algoritmo de floresta profunda: uma exploração para modelos profundos não NN baseados em módulos não diferenciáveis
Zhi-Hua Zhou (Universidade de Nanjing)
→ Apresentação
→ Artigo
Implementações - abaixo
Um professor da China falou sobre o conjunto de árvores, que os autores chamam de primeiro treinamento profundo em módulos não diferenciáveis. Pode parecer uma afirmação muito alta, mas este professor e seu índice H-95 são oradores convidados, esse fato nos permite levar a afirmação mais a sério. A teoria básica do Deep Forest foi desenvolvida há muito tempo, o artigo original já é 2017 (quase 200 citações), mas os autores escrevem bibliotecas e todos os anos aprimoram o algoritmo em velocidade. E agora, ao que parece, eles chegaram ao ponto em que esta bela teoria pode finalmente ser posta em prática.
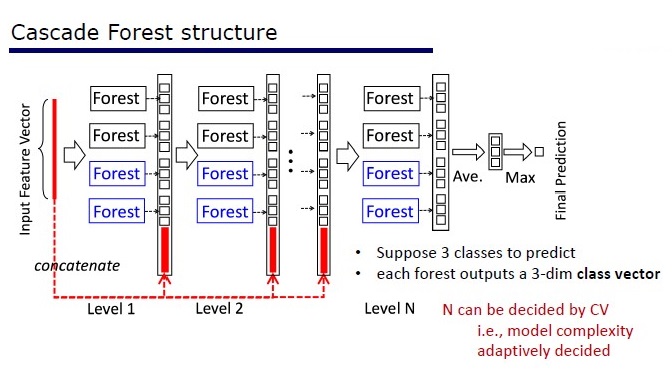
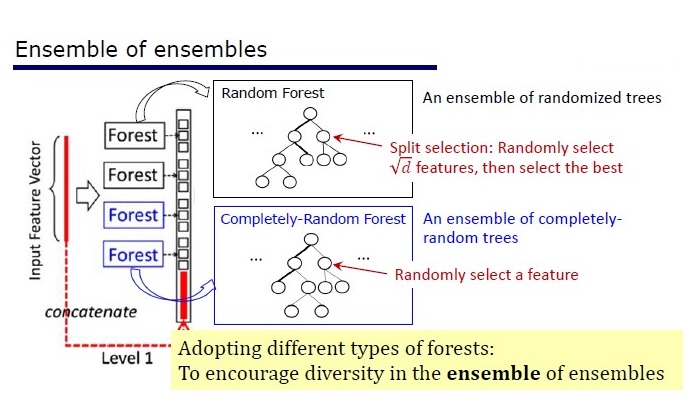
Visão geral da arquitetura Deep Forest
Antecedentes
Modelos profundos, que agora são entendidos como redes neurais profundas, são usados para capturar dependências complexas de dados. Além disso, descobriu-se que aumentar o número de camadas é mais eficiente do que aumentar o número de unidades em cada camada. Mas as redes neurais têm suas desvantagens:
- São necessários muitos dados para não treinar novamente,
- São necessários muitos recursos de computação para aprender em um período de tempo razoável,
- Muitos hiperparâmetros difíceis de configurar de maneira ideal
Além disso, elementos de redes neurais profundas são módulos diferenciáveis que não são necessariamente eficazes para cada tarefa. Apesar da complexidade das redes neurais, algoritmos conceitualmente simples, como uma floresta aleatória, geralmente funcionam melhor ou não muito pior. Mas, para esses algoritmos, é necessário projetar recursos manualmente, o que também é difícil de ser feito da melhor maneira possível.
Os pesquisadores já notaram que os conjuntos no Kaggle: são “muito perfeitos” e, inspirados pelas palavras de Scholl e Hinton, de que a diferenciação é o lado mais fraco do Deep Learning, eles decidiram criar um conjunto de árvores com propriedades de DL.
Slide “Como fazer um bom conjunto”
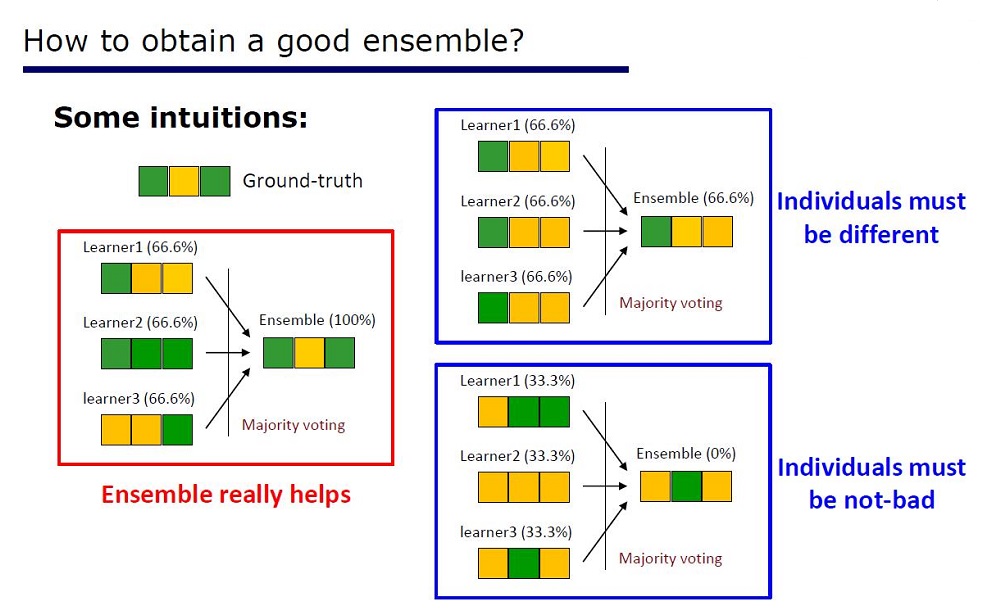
A arquitetura foi deduzida das propriedades dos conjuntos: os elementos dos conjuntos não devem ser muito pobres em qualidade e diferir.
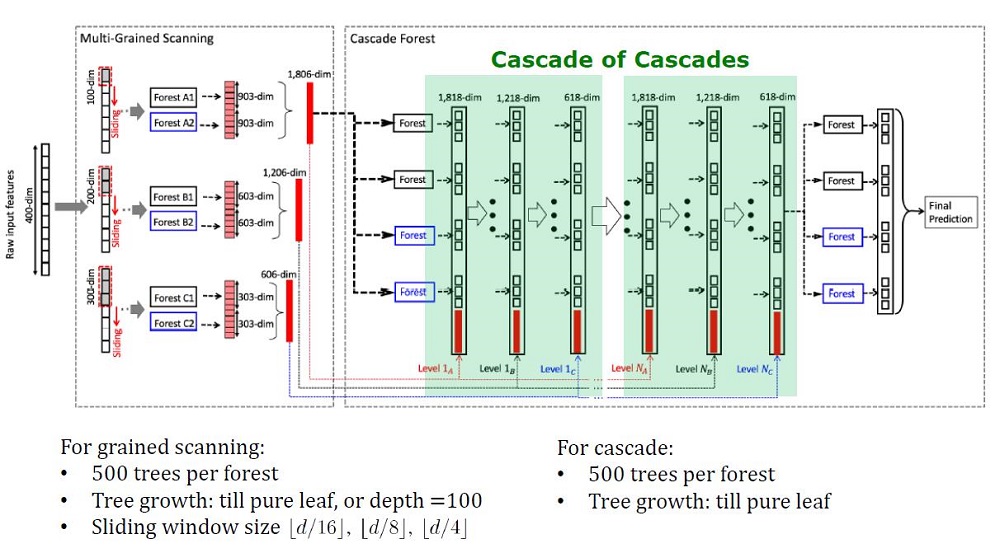
O GcForest consiste em duas fases: Floresta em cascata e Varredura de grãos múltiplos. Além disso, para que a cascata não se treine novamente, consiste em 2 tipos de árvores - uma das quais são absolutamente aleatórias que podem ser usadas em dados não alocados. O número de camadas é determinado dentro do algoritmo de validação cruzada.
Dois tipos de árvores
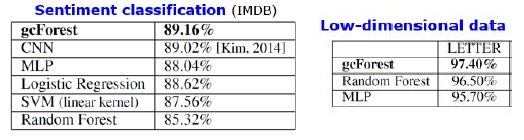
Resultados
Além dos resultados em conjuntos de dados padrão, os autores tentaram usar o gcForest em transações do sistema de pagamento chinês para procurar fraudes e obtiveram F1 e AUC muito mais altas que as de LR e DNN. Esses resultados estão apenas na apresentação, mas o código a ser executado em alguns conjuntos de dados padrão está no Git.
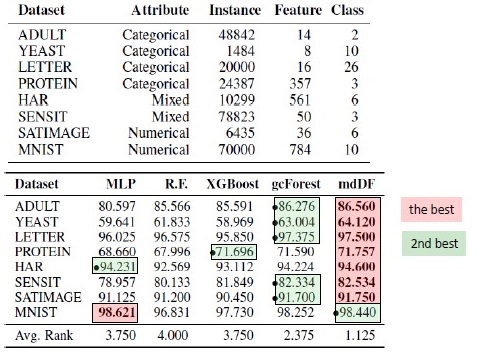
Resultados de substituição de algoritmos. mdDF é a Floresta Profunda de Distribuição de Margem ideal, uma variante do gcForest
Prós:
- Poucos hiperparâmetros, o número de camadas é ajustado automaticamente dentro do algoritmo
- As configurações padrão são escolhidas para funcionar bem em muitas tarefas.
- Complexidade adaptativa do modelo, em dados pequenos - um modelo pequeno
- Não há necessidade de definir recursos
- Funciona de qualidade comparável a redes neurais profundas e, às vezes, melhor
Contras:
- Não acelerado na GPU
- Nas fotos perde DNNs
As redes neurais têm um problema de atenuação de gradiente, enquanto as florestas profundas têm um problema de "desaparecimento da diversidade". Como esse é um conjunto, quanto mais elementos "diferentes" e "bons" forem usados, maior será a qualidade. O problema é que os autores já tentaram quase todas as abordagens clássicas (amostragem, randomização). Enquanto nenhuma nova pesquisa básica aparecer sobre o tema "diferenças", será difícil melhorar a qualidade das florestas profundas. Mas agora é possível melhorar a velocidade da computação.
Reprodutibilidade dos resultados
Fiquei intrigado com o XGBoost nos dados tabulares e queria reproduzir o resultado. Peguei o conjunto de dados Adultos e apliquei o GcForestCS (uma versão ligeiramente acelerada do GcForest) com parâmetros dos autores do artigo e o XGBoost com parâmetros padrão. No exemplo que os autores tiveram, os recursos categóricos já foram pré-processados de alguma forma, mas não foi indicado como. Como resultado, usei o CatBoostEncoder e outra métrica - ROC AUC. Os resultados foram estatisticamente diferentes - o XGBoost venceu. O tempo de operação do XGBoost é insignificante, enquanto o gcForestCS possui 20 minutos de cada validação cruzada em 5 vezes. Por outro lado, os autores testaram o algoritmo em diferentes conjuntos de dados e ajustaram os parâmetros desse conjunto de dados ao pré-processamento de seus recursos.
O código pode ser encontrado aqui .
Implementações
→ O código oficial dos autores do artigo
→ Modificação oficial aprimorada, mais rápida, mas sem documentação
→ A implementação é mais simples
PcLasso: o laço atende à regressão dos componentes principais
J. Kenneth Tay, Jerome Friedman, Robert Tibshirani (Universidade de Stanford)
→ Artigo
→ Apresentação
→ Exemplo de uso
No início de 2019, J. Kenneth Tay, Jerome Friedman e Robert Tibshirani, da Universidade de Stanford, propuseram um novo método de ensino com um professor, especialmente adequado para dados esparsos.
Os autores do artigo resolveram o problema de analisar dados sobre estudos de expressão gênica, descritos em Zeng & Breesy (2016). Alvo é o status mutacional do gene p53, que regula a expressão do gene em resposta a vários sinais de estresse celular. O objetivo do estudo é identificar preditores que se correlacionam com o status mutacional da p53. Os dados consistem em 50 linhas, 17 das quais são classificadas como normais e as 33 restantes carregam mutações no gene p53. De acordo com a análise de Subramanian et al. (2005) 308 conjuntos de genes que estão entre 15 e 500 são incluídos nesta análise. Esses kits de genes contêm um total de 4.301 genes e estão disponíveis no pacote grpregOverlap R. Ao expandir dados para processar grupos sobrepostos, são produzidas 13.237 colunas. Os autores do artigo utilizaram o método pcLasso, que ajudou a melhorar os resultados do modelo.
Na figura, vemos um aumento na AUC ao usar o "pcLasso"

A essência do método
Método combina  -regularização com
-regularização com  , que restringe o vetor de coeficientes aos principais componentes da matriz de recursos. Eles chamaram o método proposto de “componentes principais do laço” (“pcLasso” disponível em R). O método pode ser especialmente poderoso se as variáveis forem agrupadas anteriormente (o usuário escolhe o que e como agrupar). Nesse caso, o pcLasso comprime cada grupo e obtém a solução na direção dos principais componentes desse grupo. No processo de resolução, também é realizada a seleção de grupos significativos entre os disponíveis.
, que restringe o vetor de coeficientes aos principais componentes da matriz de recursos. Eles chamaram o método proposto de “componentes principais do laço” (“pcLasso” disponível em R). O método pode ser especialmente poderoso se as variáveis forem agrupadas anteriormente (o usuário escolhe o que e como agrupar). Nesse caso, o pcLasso comprime cada grupo e obtém a solução na direção dos principais componentes desse grupo. No processo de resolução, também é realizada a seleção de grupos significativos entre os disponíveis.
Apresentamos a matriz diagonal da decomposição singular de uma matriz centralizada de feições  da seguinte maneira:
da seguinte maneira:
Representamos nossa decomposição singular da matriz centralizada X (SVD) como  onde
onde  É uma matriz diagonal que consiste em valores singulares. Nesta forma
É uma matriz diagonal que consiste em valores singulares. Nesta forma  - A regularização pode ser representada:
- A regularização pode ser representada:
 onde
onde  - matriz diagonal contendo a função de quadrados de valores singulares:
- matriz diagonal contendo a função de quadrados de valores singulares: %2C%E2%80%A6%2CZ_%7B22%7D%3Df_2%20(d_1%5E2%2Cd_2%5E2%2C%E2%80%A6%2Cd_m%5E2%20)) .
.
Em geral, em  -regularização
-regularização  para todos
para todos  isso corresponde
isso corresponde  . Eles sugerem minimizar a seguinte funcionalidade:
. Eles sugerem minimizar a seguinte funcionalidade:
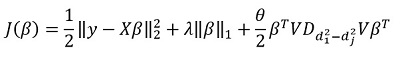
Aqui  - matriz de diferenças de elementos diagonais
- matriz de diferenças de elementos diagonais  . Em outras palavras, controlamos o vetor
. Em outras palavras, controlamos o vetor  usando hiperparâmetro também
usando hiperparâmetro também  .
.
Transformando essa expressão, obtemos a solução:
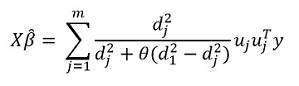
Mas a principal "característica" do método, é claro, é a capacidade de agrupar dados e, com base nesses grupos, destacar os principais componentes do grupo. Em seguida, reescrevemos nossa solução no formato:
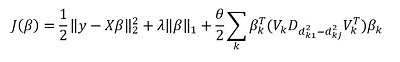
Aqui  - subvetor vector
- subvetor vector  correspondente ao grupo k,
correspondente ao grupo k, ) - valores singulares
- valores singulares  dispostos em ordem decrescente, e
dispostos em ordem decrescente, e  - matriz diagonal
- matriz diagonal 
Algumas notas sobre a solução do destino funcional:
A função objetivo é convexa e o componente não suave é separável. Portanto, ele pode ser efetivamente otimizado usando a descida do gradiente.
A abordagem é comprometer vários valores  (incluindo zero, respectivamente, obtendo o padrão
(incluindo zero, respectivamente, obtendo o padrão  -regularization) e, em seguida, otimize:
-regularization) e, em seguida, otimize:  pegando
pegando  . Assim, os parâmetros
. Assim, os parâmetros  e
e  são selecionados para validação cruzada.
são selecionados para validação cruzada.
Parâmetro  difícil de interpretar. No software (pacote pcLasso), o próprio usuário define o valor desse parâmetro, que pertence ao intervalo [0,1], em que 1 corresponde a
difícil de interpretar. No software (pacote pcLasso), o próprio usuário define o valor desse parâmetro, que pertence ao intervalo [0,1], em que 1 corresponde a  = 0 (laço).
= 0 (laço).
Na prática, variar os valores  = 0,25, 0,5, 0,75, 0,9, 0,95 e 1, você pode cobrir uma ampla variedade de modelos.
= 0,25, 0,5, 0,75, 0,9, 0,95 e 1, você pode cobrir uma ampla variedade de modelos.
O algoritmo em si é o seguinte

Este algoritmo já está escrito em R, se desejar, você já pode usá-lo. A biblioteca é chamada 'pcLasso'.
Um canivete infinitesimal do exército suíço
Ryan Giordano (UC Berkeley); William Stephenson (MIT); Runjing Liu (UC Berkeley);
Michael Jordan (UC Berkeley); Tamara Broderick (MIT)
→ Artigo
→ Código
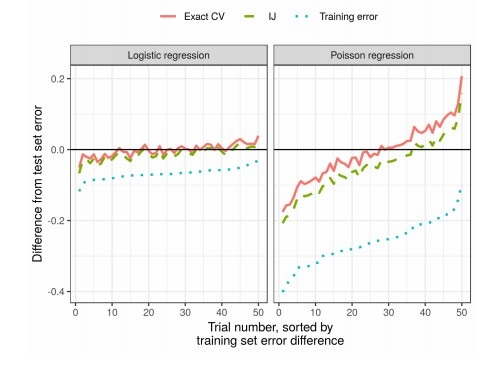
A qualidade dos algoritmos de aprendizado de máquina é frequentemente medida por validação cruzada múltipla (validação cruzada ou autoinicialização). Esses métodos são poderosos, mas lentos em grandes conjuntos de dados.
Neste trabalho, os colegas usam aproximação linear de pesos, produzindo resultados que funcionam mais rapidamente. Essa aproximação linear é conhecida na literatura estatística como "canivete infinitesimal". É utilizado principalmente como ferramenta teórica para comprovação de resultados assintóticos. Os resultados do artigo são aplicáveis independentemente de os pesos e os dados serem estocásticos ou determinísticos. Como conseqüência, essa aproximação estima sequencialmente a verdadeira validação cruzada para qualquer k fixo.
Apresentação do Paper Award ao autor do artigo

A essência do método
Considere o problema de estimar um parâmetro desconhecido  onde
onde  É compacto e o tamanho do nosso conjunto de dados é
É compacto e o tamanho do nosso conjunto de dados é  . Nossa análise será realizada em um conjunto de dados fixo. Definir nossa classificação
. Nossa análise será realizada em um conjunto de dados fixo. Definir nossa classificação  da seguinte maneira:
da seguinte maneira:
- Para cada
 definir
definir  (
(  ) É uma função de
) É uma função de 
 É um número real e
É um número real e  É um vetor que consiste em
É um vetor que consiste em 
Então  pode ser representado como:
pode ser representado como:

Resolvendo esse problema de otimização pelo método do gradiente, assumimos que as funções são diferenciáveis e podemos calcular o Hessian. O principal problema que resolvemos é o custo computacional associado à avaliação ) para todos
para todos  . A principal contribuição dos autores é calcular
. A principal contribuição dos autores é calcular ) onde
onde ) . Em outras palavras, nossa otimização dependerá apenas de derivativos
. Em outras palavras, nossa otimização dependerá apenas de derivativos ) que assumimos que existem e são hessianos:
que assumimos que existem e são hessianos:
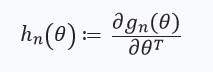
Em seguida, definimos uma equação com um ponto fixo e sua derivada:
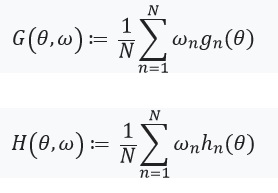
Aqui vale a pena prestar atenção que %2Cw)%3D0) desde
desde ) - solução para
- solução para %3D0) . Também definimos:
. Também definimos: ) e a matriz de pesos como:
e a matriz de pesos como:  . No caso em que
. No caso em que  tem uma matriz inversa, podemos usar o teorema da função implícita e a 'regra da cadeia':
tem uma matriz inversa, podemos usar o teorema da função implícita e a 'regra da cadeia':
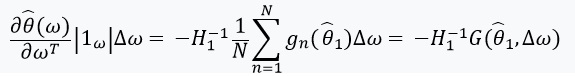
Essa derivada nos permite formar uma aproximação linear ) através de
através de  que se parece com isso:
que se parece com isso:
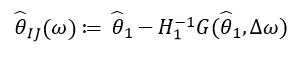
Desde  depende apenas de
depende apenas de  e
e  , e não de soluções para outros valores
, e não de soluções para outros valores  , portanto, não há necessidade de recalcular e encontrar novos valores de ω. Em vez disso, é preciso resolver o LES (sistema de equações lineares).
, portanto, não há necessidade de recalcular e encontrar novos valores de ω. Em vez disso, é preciso resolver o LES (sistema de equações lineares).
Resultados
Na prática, isso reduz significativamente o tempo em comparação com a validação cruzada: