Alexey Savvateev: Modelos de Internet e redes sociais

"A única razão para a existência da economia é inspirar os matemáticos para novas façanhas."



Em 2013, Alexey Savvateev deu várias palestras sobre modelos de redes sociais e Internet. Achei esse tópico muito curioso e imerecidamente esquecido. Vamos tentar entender o problema. Também estou interessado em saber como a situação mudou desde então e quais são as publicações úteis nessa área.

Tanto na Internet quanto na biologia das redes sociais, elas exibem propriedades que são descritas individualmente por modelos, mas todas juntas - elas confundem a matemática moderna. Savvateev afirma que "quem lida com isso receberá o Prêmio Nobel". O futuro dependerá da capacidade de trabalhar com redes.

A seguir, é apresentada uma compilação de três vídeos de palestras, o vídeo em si está no final. (A publicação parece um conjunto de slides com citações de conferencistas. Para vincular tudo a um texto único e elegante, não tenho habilidades para o idioma e a matemática russos, mas o tópico é muito importante, por isso quero publicá-lo.)

A rede social consiste em:

• Agentes
• Comunicações entre agentes

As conexões podem ser de mão dupla (amigos, co-autoria) e podem ser de mão única (assinantes). O social sempre existiu, mas estudá-los no nível macro tornou-se possível apenas com o advento das redes online. A humanidade nos últimos 10 anos deu um salto quântico. Aprendeu a examinar tudo de si como um todo. Pode digitalizar. Reúna informações sobre você.

Seria justo construir um modelo de gráficos ponderados quando os coeficientes da “força de união” são indicados. Mas para nós como antes para a lua.

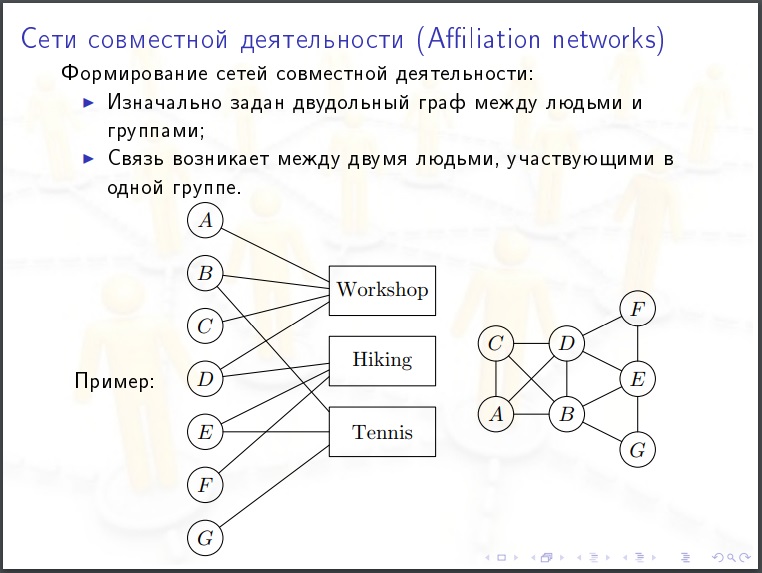
Galeria

É útil olhar para as fotos. A hipótese que você poderia apresentar depois de ver a foto pode ser obviamente absurda.

Quem é útil para estudar redes sociais

Economia: Supõe-se que os níveis micro e macro da economia estejam conectados através de uma “rede”
Ciência política: Supõe-se se o regime permanecerá ou mudará, dependendo de quem terá especialistas em redes mais poderosos.



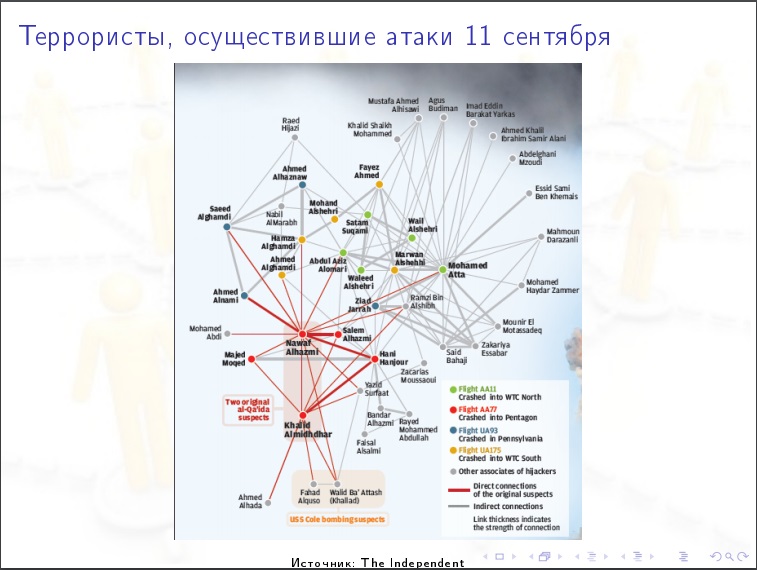Exemplo de análise de mídia social.

Características numéricas das redes sociais

• Distância
• Diâmetro
• Grau de vértice
• Distribuição de graus de vértice
• Medidas de centralidade do nó
• Distribuição centralizada
• Coeficiente de cluster
• Coeficiente de sortimento

Distância - quantas arestas você precisa passar para passar de um vértice para outro.

Diâmetro é a distância máxima no gráfico.

O grau de um vértice é o número de arestas no vértice.

Teoria dos Seis Apertos de Mão

Qualquer gráfico social tem um diâmetro médio muito baixo ( Teoria dos Seis Apertos de Mão ). Além disso, há um núcleo muito denso. Estou "familiarizado" com alguns africanos, através do meu presidente, que apertaram a mão do presidente africano.







Coeficiente de armazenamento em cluster local . Nós olhamos para todos os vizinhos de uma pessoa, "k" pedaços. Costelas máximas - k (k-1) / 2. Observamos o número real de arestas e dividimos por esse máximo.

Fator de agrupamento global . Quantos "triângulos" em comparação com as "marcas de verificação".





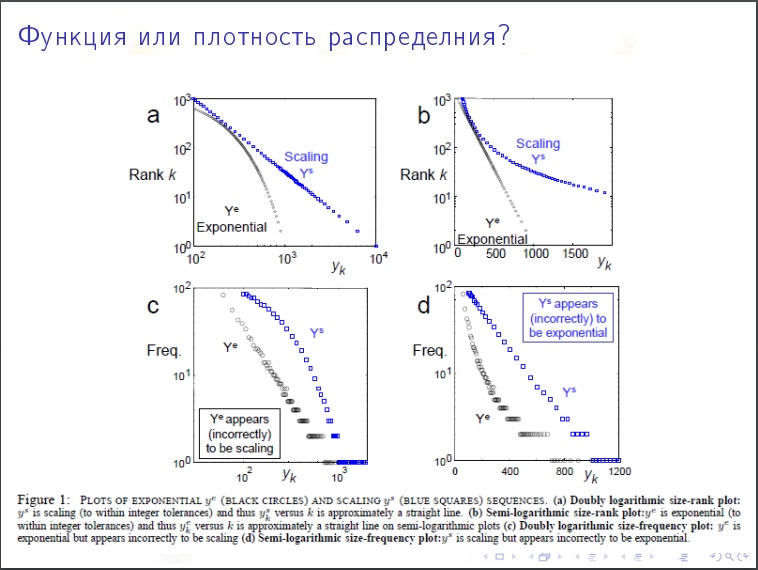
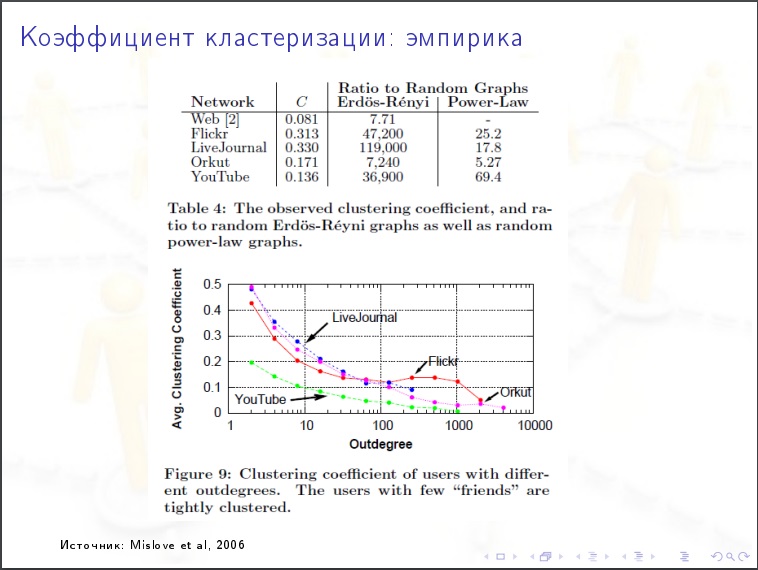A distribuição de graus do vértice . Qual% dos vértices tem graus inferiores a 1000? A natureza da distribuição é exponencial ou exponencial? Acontece que a Internet tem uma natureza tranqüila.

O coeficiente é "2". Os vértices cujo grau é "x" serão N / x ² . Verificamos que em LJ um bilhão de usuários, milésimos milésimos devem ser divididos por mil a mil ao quadrado. Milésimos milésimos.

Isso é uma coisa que diminui muito lentamente.













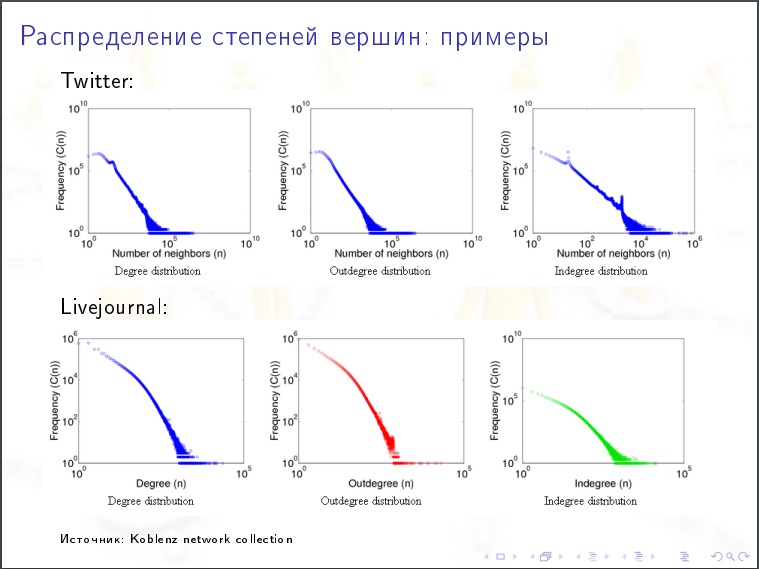
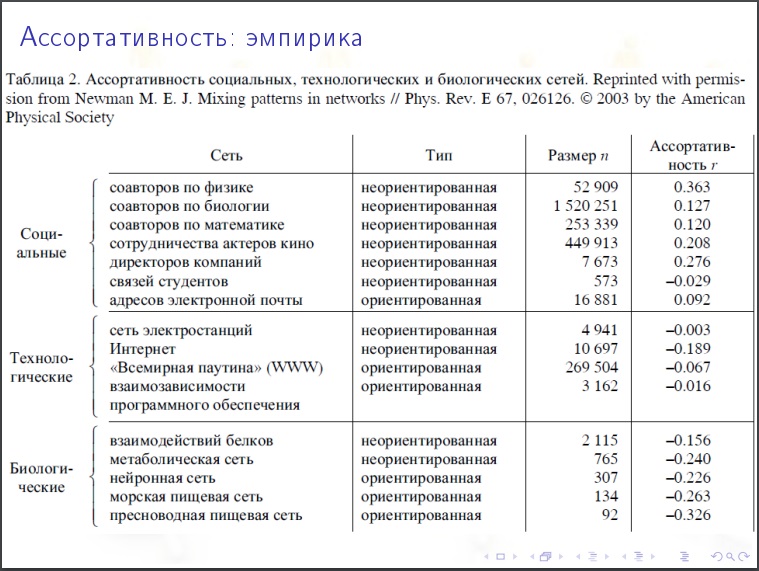
Coeficiente de sortimento . abordagem aproximada - tomamos picos com aproximadamente o mesmo número de graus, é mais provável que eles estejam conectados entre si ou com menos? Se sim, então é sortido. Dissortatividade - quando com um grande número de graus, é mais provável que associado a menos. Essa é uma abordagem ingênua. Uma abordagem mais correta é essa. Em cada vértice, há outra característica (capital total do banco), e a classificação por esse indicador parece.





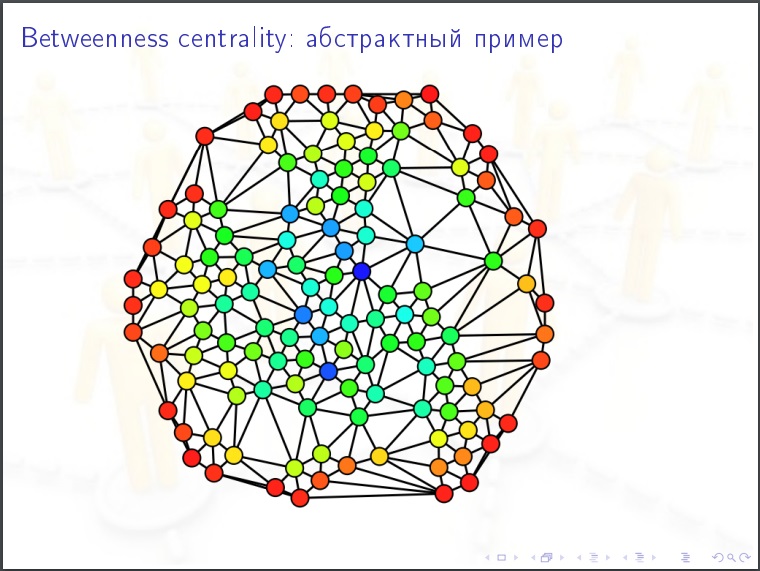
A centralidade do nó para uma rede social. Pegamos uma pessoa, consideramos o seguinte valor para ela. Classificamos todos os pares de outras pessoas (N-1) (N-2) / 2 e, em cada caso, perguntamos, o caminho de namoro mais próximo no gráfico, ele passa por essa pessoa? Pode haver vários caminhos mais curtos e alguns deles contêm nossa pessoa, então damos a ele%. Essa é a característica mais importante nas redes sociais. Para a propagação de epidemias, opinião pública. É isso que precisa ser medido.









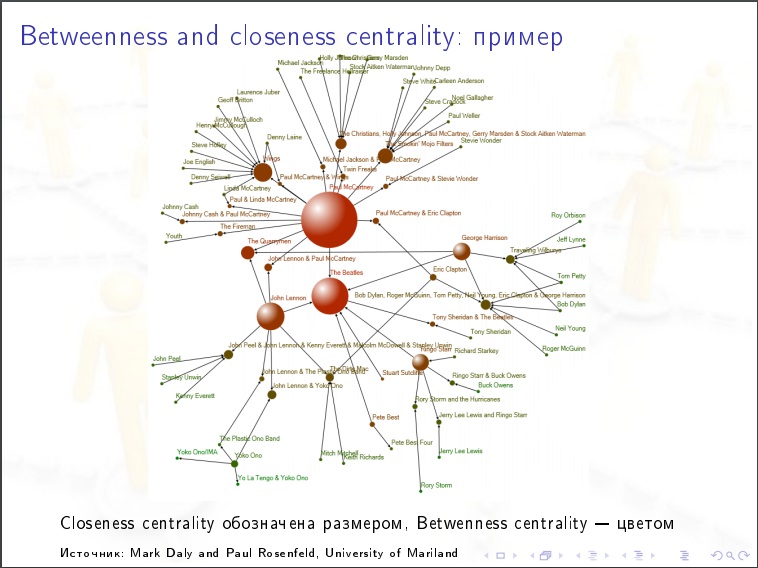
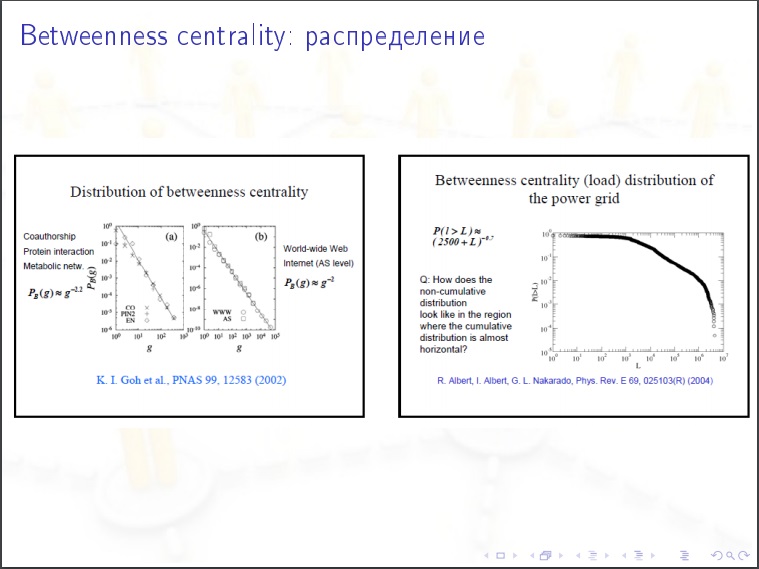
Recursos das redes sociais:

• Pequeno diâmetro e distância média entre vértices
• A lei da potência da distribuição de graus de vértices e centralidade de entrelaçamento
• Alta taxa de agrupamento
• Sortimento
• A presença de um núcleo intimamente relacionado

A tarefa é criar um modelo que cubra as três primeiras propriedades (e de preferência as duas últimas). Os três primeiros já são de complexidade intransponível neste momento. Para 2013, não existe esse modelo.

Passamos à descrição dos modelos de gráficos aleatórios que existiam.

Modelos

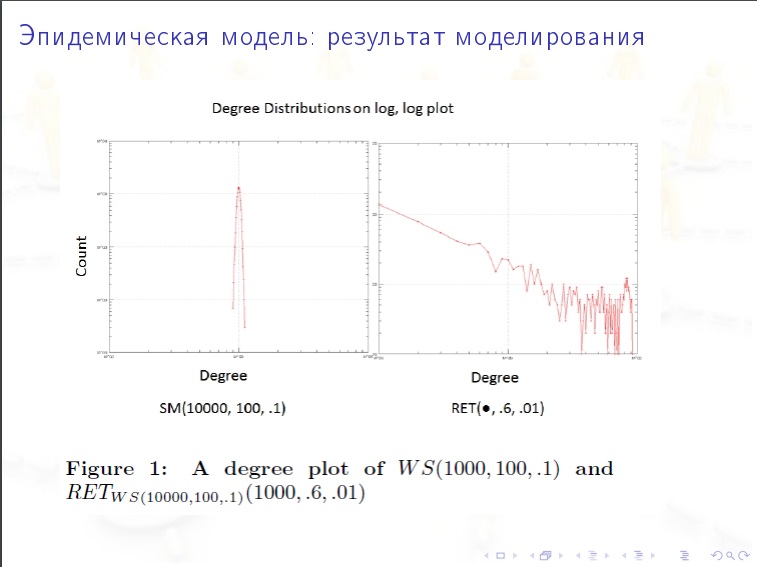
Os modelos são:

• Técnico (as arestas são geradas aleatoriamente)
• Teórica do jogo (quando é benéfico para alguém)
• Sem estrutura (apenas muitos vértices)
• Estrutural (os vértices são pontos do espaço métrico ou têm pesos; existe uma estrutura no conjunto de vértices)

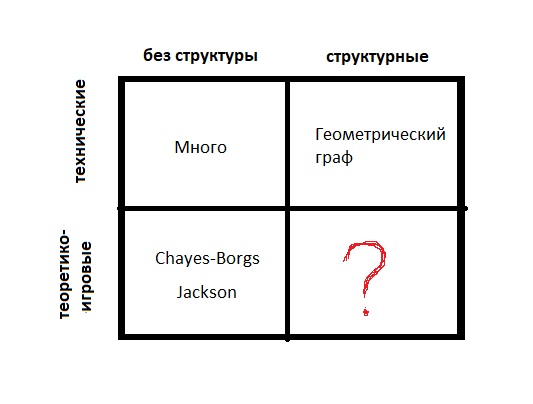
Se você entende o que é subjacente, pode ser guiado por um número muito grande de parâmetros. Se os parâmetros bem escolhidos fornecerem uma boa aproximação, você estará bem. E mesmo que a melhor combinação dê um resultado ruim e não seja consistente com os fatos observados, então adeus.

Tudo isso é feito com um propósito - combater o spam.

A Internet pode ser imaginada como uma rede complexa em vários níveis:

• Nível tecnológico . Vértices e arestas são nós e linhas de comunicação.
• Nível de hipertexto . Os vértices são sites ou páginas e as bordas são hiperlinks.
• Nível social . Os vértices são usuários e as arestas são aquelas ou outras conexões entre eles: amizades nas redes sociais, assinatura de blogs, colaboração em projetos distribuídos (por exemplo, wikipedia), etc.

Para redes complexas, muitas características numéricas locais e globais são conhecidas: a distribuição de graus de vértices, o coeficiente de agrupamento, o coeficiente de sortimento

Acontece que vários recursos são característicos das redes da Internet:

• Distribuição de graus Paretto
• alto coeficiente de agrupamento,
• sortimento positivo
• pequeno diâmetro.

O objetivo final da modelagem de redes da Internet é construir modelos com os mesmos recursos.

Modelo Erdos - Renyi

O modelo Erdos - Renyi é um dos dois modelos de geração aleatória de gráficos intimamente relacionados. Os modelos têm o nome dos matemáticos Pal Erdös e Alfred Renyi, que foram os primeiros a introduzir um dos modelos em 1959. Explorou o gráfico de namoro.

Considere N pontos. Bordas potenciais - N * (N-1) / 2. Para cada costela, realizamos um teste aleatório. A probabilidade de a costela ter acontecido - p. O que não aconteceu - (1-p). Vamos fazer o "teste", temos um gráfico. Mas existem alguns problemas. Para que a propriedade "escassez" apareça, p deve ser muito pequeno, da ordem de 1 / N, e então o diâmetro será muito grande.

Qualquer pesquisador que ouça que a Internet é descrita como um gráfico aleatório de acordo com o modelo Erds-Renyi rirá.

Um efeito interessante é que, quando você supera um certo limite de probabilidade, o gráfico se torna conectado.

Bollobashi Model

Este é um modelo dinâmico para construir a Internet. Estamos tentando adivinhar como se formou gradualmente. A ideia é essa. Tomamos um gráfico com um vértice e uma aresta e, a cada passo, reproduzimos aleatoriamente. Adicionamos um vértice, depois disso, com alguma probabilidade, ele se fecha e, com alguma probabilidade, se conecta ao anterior. O próximo pico com alguma probabilidade se fecha e, com alguns, vai para um dos anteriores. Além disso, a probabilidade de atingir o topo é sempre proporcional ao número de arestas que são. Um valor aleatório é reproduzido e o próximo sorteio depende do resultado do anterior. Esse modelo é intuitivo, mas matematicamente difícil de calcular. Este modelo fornece uma distribuição de energia não exponencial. O diâmetro é o mesmo.

Mas esse modelo não funciona com cluster.

Existem duas abordagens concorrentes que trabalham com clustering.

Abordagem geométrica

A suposição é retirada do teto. O gráfico da Internet é baseado no espaço métrico. O espaço de gostos, interesses, preferências. Como as pessoas são interessantes uma para a outra. Quão próximo em espírito, em opinião. Se as pessoas estão próximas, elas se referem uma à outra.

Pegamos e jogamos 10 ¹⁰ pontos neste espaço. Um grande número de parâmetros aparece aqui. Enorme

O agrupamento é excelente, mas os vértices decrescentes são exponenciais. Controvérsia.

Este método é extremamente simples e os algoritmos são feitos "por acaso".

Abordagem teórica dos Game-Borgs

Você sabia que nos dias de von Neumann foi anunciado que a teoria dos jogos seria uma arma de nova geração contra a União Soviética?

Assumimos que as pessoas tomam decisões para se comunicar ou não.

Organizamos reuniões / eventos. Um evento é uma lista de convidados, bem como sua "intensidade".
Custos = Intensidade * (constante + K * (número de convidados)). Eu tenho que gastar recursos para "vender" o evento e tenho que gastar mais com cada participante. Há aniversários e caminhadas. Aparece o coeficiente "P", pequeno para um aniversário e grande para uma caminhada. Intensidade de namoro.

Uma pessoa pode organizar vários eventos com intensidades P ₁ , P ₂ ... P _n . Outros fazem o mesmo.

Existem minhas ações para estabelecer laços sociais e há estranhos.

Função vencedora = (o número de pessoas com as quais você se familiarizou) - custos

“Familiar o suficiente” significa que a soma das intensidades de todos os eventos em que vocês estavam juntos é maior que um determinado valor limite. E não importa quem organizou o evento.

Costelas são mantidas por bons conhecidos o suficiente.



Está provado que muitas propriedades de fechamento real são obtidas neste modelo. Em todos os equilíbrios de Nash, também são observadas propriedades reais de fechamento e propriedades de cluster ainda mais fortes, que também são observadas no gráfico da Internet real.



Mas nada está claro sobre as outras propriedades, mas isso é metade do problema. O problema é que, se há pelo menos um equilíbrio de Nash, onde pelo menos duas pessoas se conhecem, existe um equilíbrio de Nash, no qual todos estão familiarizados com todos.





Existe uma ideia para combinar as duas abordagens. Considerar que as pessoas vivem em um espaço métrico e, quando organizam eventos ou participam de um evento, as taxas de custo, intensidade e limite dependem da "proximidade". Esta é a quinta geração de modelos.

Custos diferenciados

As opções são fazer custos diferenciados e ganhos diferenciados. Alguns são mais fáceis de convidar do que outros. O conhecimento de um é mais rentável do que o conhecimento de outro.





Suponha que organizemos todas as pessoas uniformemente em torno da circunferência. E é mais barato convidar alguém que está mais perto. Como será a balança? Todo mundo vai convidar algum bairro, certo? Não é verdade. Não existe esse equilíbrio.

Prova. Suponha que exista, então as pessoas próximas umas das outras já são convidadas para muitas reuniões diferentes. Então ele não precisa convidar esse ente querido. A existência desse equilíbrio contradiz a existência desse equilíbrio.



Existe um equilíbrio puro, é o único. Cada um convida um bairro que fica (ou no sentido anti-horário) a uma certa distância e um certo comprimento.

(- Esta é a formação de galáxias!)
(- É uma quebra espontânea de simetria!)

Conclusões

Pelevin escreveu certa vez que "o significado da vida russa está no dourado sem pressa de uma imensa iconostase". Este é o significado da matemática - da mesma forma. Somente a iconostase é científica.



Este é um estudo altamente multidisciplinar. Mais alto que você pode imaginar.

Fontes

PS

“Uma vez que fui chamado para o clube em Navalny, há alguns jovens, entusiastas que o ajudam. Eu imediatamente avisei que diria coisas desagradáveis. Uma revolução é vitoriosa se os matemáticos que são a favor da revolução são mais fortes do que aqueles que são contra. Os jovens de Navalny não sabiam como contar esses modelos para eles, mas eles não entendem, nem sabem como se integrar - apenas correm e gritam em algum lugar. E contra eles está uma instituição forte, com pessoas sérias à frente, que, por ordem do Kremlin, diz quem exatamente e quanto deve ser preso para que não haja nada. Eles dizem: "Somos descentralizados - especificamente Navalny não significa nada, existem vários líderes importantes". E então um matemático chega e acredita que a centralização é 90% dessa rede. Você bloqueia alguém de que precisa por alguns dias - e não há revolução. A matemática vence.
- Alexey Savvateev, "A revolução vence se tiver bons matemáticos"

PPS

Quem sabe que outros trabalhos interessantes (artigos, palestras) existem trabalhos no campo das redes sociais e seus benefícios práticos, por favor, compartilhe.