Redes neurais e aprendizado profundo, capítulo 3, parte 1: melhorando a maneira como as redes neurais são treinadas

Quando uma pessoa aprende a jogar golfe, geralmente passa a maior parte do tempo realizando um golpe básico. Ele então aborda outros golpes, gradualmente, estudando esses ou aqueles truques, com base no golpe básico e desenvolvendo-o. Da mesma forma, até agora focamos no entendimento do algoritmo de retropropagação. Este é o nosso "ataque básico", a base para o treinamento da maior parte do trabalho com redes neurais (SN). Neste capítulo, falarei sobre um conjunto de técnicas que podem ser usadas para melhorar nossa implementação mais simples de retropropagação e para melhorar a maneira de ensinar NS.

Entre as técnicas que aprenderemos neste capítulo estão: a melhor opção para o papel da função de custo, a saber, a função de custo com entropia cruzada; quatro chamados métodos de regularização (regularização de L1 e L2, exclusão de neurônios [abandono], extensão artificial dos dados de treinamento), que melhoram a generalização de nossa SN além dos limites dos dados de treinamento; melhor método para inicializar pesos de rede; um conjunto de métodos heurísticos para ajudá-lo a escolher bons hiperparâmetros para a rede. Também vou considerar várias outras técnicas, um pouco mais superficialmente. Na maioria das vezes, essas discussões são independentes uma da outra, para que você possa pular sobre elas, se desejar. Também implementamos muitas tecnologias no código de trabalho e as usamos para melhorar os resultados obtidos para a tarefa de classificação de números manuscritos, estudada no Capítulo 1.

Obviamente, consideramos apenas uma fração do grande número de técnicas desenvolvidas para uso em redes neurais. A conclusão é que a melhor maneira de entrar no mundo da abundância de técnicas disponíveis é estudar em detalhes algumas das mais importantes. O domínio dessas técnicas importantes não é apenas útil por si só, mas também aprofundará sua compreensão dos problemas que podem surgir ao usar redes neurais. Como resultado, você estará preparado para adaptar rapidamente novas técnicas, conforme necessário.

Função de custo de entropia cruzada

Muitos de nós odeiam estar errados. Logo depois de começar a aprender piano, dei um pequeno concerto na frente de uma platéia. Eu estava nervoso e comecei a tocar uma peça uma oitava abaixo do necessário. Fiquei confuso e não pude continuar até que alguém apontasse um erro para mim. Eu estava com muita vergonha. No entanto, embora isso seja desagradável, também aprendemos muito rapidamente, decidindo que estávamos errados. E certamente da próxima vez que falei com o público, toquei na oitava certa! Por outro lado, aprendemos mais lentamente quando nossos erros não estão bem definidos.

Idealmente, esperamos que nossas redes neurais aprendam rapidamente com seus erros. Isso acontece na prática? Para responder a essa pergunta, vejamos um exemplo absurdo. Envolve um neurônio com apenas uma entrada:



Estamos ensinando esse neurônio a fazer algo ridiculamente simples: aceite 1 e dê 0. É claro que poderíamos encontrar uma solução para um problema tão trivial selecionando manualmente o peso e o deslocamento, sem usar o algoritmo de treinamento. No entanto, será bastante útil tentar usar a descida do gradiente para obter peso e deslocamento como resultado do treinamento. Vejamos como um neurônio é treinado.

Por definição, vou escolher um peso inicial de 0,6 e um deslocamento inicial de 0,9. Esses são alguns valores gerais atribuídos como ponto de partida e eu não os selecionei especificamente. Inicialmente, um neurônio de saída produz 0,82; portanto, precisamos aprender muito para chegar perto da saída desejada de 0,0. O artigo original possui um formulário interativo no qual você pode clicar em "Executar" e observar o processo de aprendizado. Essa animação não é pré-gravada, o navegador calcula o gradiente e, em seguida, usa-o para atualizar o peso e o deslocamento e mostra o resultado. A velocidade de aprendizado é η = 0,15, lenta o suficiente para poder ver o que está acontecendo, mas rápida o suficiente para que a aprendizagem ocorra em segundos. A função de custo C é quadrática, introduzida no primeiro capítulo. Em breve vou lembrá-lo de sua forma exata, portanto não é necessário voltar e vasculhar lá. O treinamento pode ser iniciado várias vezes, basta clicar no botão "Executar".

Como você pode ver, o neurônio aprende rapidamente o peso e o viés, o que diminui o custo e produz uma saída de 0,09. Este não é o resultado desejado de 0,0, mas é muito bom. Suponha que escolhemos um peso inicial e um deslocamento de 2,0. Nesse caso, a saída inicial será 0,98, o que está completamente errado. Vamos ver como, nesse caso, o neurônio aprenderá a produzir 0.

Embora este exemplo use a mesma taxa de aprendizado (η = 0,15), vemos que o aprendizado é mais lento. Cerca de 150 das primeiras épocas, pesos e deslocamentos dificilmente mudam. Em seguida, o treinamento acelera e, quase como no primeiro exemplo, o neurônio se move rapidamente para 0,0. esse comportamento é estranho, não é como aprender uma pessoa. Como eu disse no começo, geralmente aprendemos mais rapidamente quando estamos muito enganados. Mas acabamos de ver como nosso neurônio artificial aprende com grande dificuldade, cometendo muitos erros - muito mais difícil do que quando ele cometeu um pequeno erro. Além disso, verifica-se que esse comportamento surge não apenas em nosso exemplo simples, mas também em um NS de propósito mais geral. Por que o aprendizado é tão lento? Posso encontrar uma maneira de evitar esse problema?

Para entender a fonte do problema, lembramos que nosso neurônio aprende através de alterações no peso e no deslocamento a uma taxa determinada pelas derivadas parciais da função de custo, ∂C / ∂w e ∂C / ∂b. Dizer "aprender é lento" é o mesmo que dizer que essas derivadas parciais são pequenas. O problema é entender por que eles são pequenos. Para fazer isso, vamos calcular as derivadas parciais. Lembre-se de que usamos a função de custo quadrático, que é dada pela equação (6):

$$

$$C = \ frac {(y-a) ^ 2} {2} \ tag {54}$$

onde a é a saída do neurônio quando x = 1 é usado na entrada e y = 0 é a saída desejada. Para escrever isso diretamente por meio de peso e deslocamento, lembre-se de que a = σ (z), onde z = wx + b. Utilizando a regra da cadeia para diferenciação por peso e deslocamento, obtemos:

$$

$$\ frac {\ parcial C} {\ parcial w} = (a-y) \ sigma '(z) x = a \ sigma' (z) \ tag {55}$$

$$

$$\ frac {\ parcial C} {\ parcial b} = (a-y) \ sigma '(z) = a \ sigma' (z) \ tag {56}$$

onde substituí x = 1 e y = 0. Para entender o comportamento dessas expressões, vamos dar uma olhada no termo σ '(z) à direita. Lembre-se da forma de um sigmóide:



O gráfico mostra que quando a saída do neurônio está próxima de 1, a curva se torna muito plana e σ '(z) se torna pequeno. As equações (55) e (56) nos dizem que ∂C / ∂w e ∂C / ∂b se tornam muito pequenos. Daí a desaceleração na aprendizagem. Além disso, como veremos um pouco mais tarde, a desaceleração do treinamento ocorre, de fato, pela mesma razão e na Assembléia Nacional de natureza mais geral, e não apenas no nosso exemplo mais simples.

Introdução à função de custo de entropia cruzada

O que fazemos com a desaceleração do aprendizado? Acontece que podemos resolver o problema substituindo a função quadrática do valor por outra função do valor, conhecida como entropia cruzada. Para entender a entropia cruzada, nos afastamos de nosso modelo mais simples. Suponha que treinemos um neurônio com vários valores de entrada x ₁ , x ₂ , ... pesos correspondentes w ₁ , w ₂ , ... e deslocamento b:



A saída do neurônio, é claro, será a = σ (z), onde z = w _j w _j x _j + b é a soma ponderada das entradas. Definimos a função de custo da entropia cruzada para um dado neurônio como

$$

$$C = - \ frac {1} {n} \ sum_x \ left [y \ n em um + (1-y) \ ln (1-a) \ right] \ tag {57}$$

onde n é o número total de unidades de dados de treinamento, a soma passa por todos os dados de treinamento xey é a saída desejada correspondente.

Não é óbvio que a equação (57) resolve o problema de diminuir a velocidade da aprendizagem. Honestamente, nem é óbvio que faça sentido chamá-lo de uma função de valor! Antes de voltarmos à desaceleração do aprendizado, vejamos em que sentido a entropia cruzada pode ser interpretada como uma função do valor.

Duas propriedades em particular tornam razoável a interpretação da entropia cruzada como uma função do valor. Em primeiro lugar, é maior que zero, ou seja, C> 0. Para ver isso, observe que (a) todos os membros individuais da soma em (57) são negativos, pois os dois logaritmos são obtidos de números no intervalo de 0 a 1 e (b) o sinal de menos está na frente da soma.

Em segundo lugar, se a saída real do neurônio estiver próxima da saída desejada para todas as entradas de treinamento x, a entropia cruzada será próxima de zero. Para provar isso, precisaremos assumir que as saídas desejadas y serão 0 ou 1. Normalmente, isso acontece ao resolver problemas de classificação ou ao calcular funções booleanas. Para entender o que acontece se você não fizer essa suposição, consulte os exercícios no final da seção.

Para provar isso, imagine que y = 0 e a≈0 para alguma entrada x. Assim será quando o neurônio lidar bem com essa entrada. Vemos que o primeiro termo da expressão (57) para o valor desaparece, já que y = 0, e o segundo será −ln (1 - a) ≈0. O mesmo acontece quando y = 1 e a≈1. Portanto, a contribuição do valor será pequena se a saída real estiver próxima da desejada.

Resumindo, entendemos que a entropia cruzada é positiva e tende a zero quando o neurônio calcula melhor a saída desejada y para todas as entradas de treinamento x. Esperamos a presença de ambas as propriedades na função de custo. E, de fato, essas duas propriedades são cumpridas pelo valor quadrático. Portanto, para entropia cruzada é uma boa notícia. No entanto, a função de custo de entropia cruzada tem uma vantagem porque, diferentemente do valor quadrático, evita o problema de diminuir a velocidade da aprendizagem. Para ver isso, vamos calcular a derivada parcial do valor com entropia cruzada por peso. Substitua a = σ (z) em (57), aplique a regra da cadeia duas vezes e obtenha

$$

$$\ frac {\ parcial C} {\ parcial w_j} = - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ direita) \ frac {\ parcial \ sigma} {\ parcial w_j} \ tag {58}$$

$$

$$= - \ frac {1} {n} \ sum_x \ left (\ frac {y} {\ sigma (z)} - \ frac {(1-y)} {1- \ sigma (z)} \ right) \ sigma '(z) x_j \ tag {59}$$

Reduzindo a um denominador comum e simplificando, obtemos:

$$

$$\ frac {\ parcial C} {\ parcial w_j} = \ frac {1} {n} \ sum_x \ frac {\ sigma '(z) x_j} {\ sigma (z) (1- \ sigma (z)) } (\ sigma (z) -y). \ tag {60}$$

Usando a definição de sigmóide, σ (z) = 1 / (1 + e ^−z ) e um pouco de álgebra, podemos mostrar que σ ′ (z) = σ (z) (1 - σ (z)). Pedirei que você verifique isso mais adiante no exercício, mas, por enquanto, aceite-o como a verdade. Os termos σ (z) e σ (z) (1 - σ (z)) são cancelados e isso leva a

$$

$$\ frac {\ parcial C} {\ parcial w_j} = \ frac {1} {n} \ sum_x x_j (\ sigma (z) -y). \ tag {61}$$

Ótima expressão. Daqui resulta que a velocidade com que os pesos são treinados é controlada por σ (z) -y, isto é, por um erro na saída. Quanto maior o erro, mais rápido o neurônio aprende. Isso poderia ser esperado intuitivamente. Esta opção evita a desaceleração no aprendizado causada pelo termo σ '(z) em uma equação de custo quadrático semelhante (55). Quando usamos entropia cruzada, o termo σ '(z) é reduzido e não precisamos mais nos preocupar com sua pequenez. Essa redução é um milagre especial garantido pela função de custo de entropia cruzada. De fato, é claro, isso não é um milagre. Como veremos mais adiante, a entropia cruzada foi escolhida especificamente para essa propriedade.

Da mesma forma, a derivada parcial para o viés pode ser calculada. Não darei todos os detalhes novamente, mas você pode verificar facilmente se

$$

$$\ frac {\ parcial C} {\ parcial b} = \ frac {1} {n} \ sum_x (\ sigma (z) -y). \ tag {62}$$

Isso novamente ajuda a evitar o atraso no aprendizado devido ao termo σ '(z) em uma equação semelhante para o valor quadrático (56).

Exercício

• Verifique se σ ′ (z) = σ (z) (1 - σ (z)).

Vamos voltar ao nosso exemplo absurdo com o qual brincamos anteriormente e ver o que acontece se usarmos entropia cruzada em vez do valor quadrático. Para sintonizar, começamos com o caso em que o custo quadrático funcionou perfeitamente quando o peso inicial era 0,6 e a compensação era 0,9. O artigo original possui uma forma interativa na qual você pode clicar no botão Executar e ver o que acontece quando você substitui o valor quadrático por entropia cruzada.

Não é de surpreender que o neurônio neste caso seja treinado perfeitamente, como antes. Agora, vamos ver o caso em que o neurônio ficava preso , com peso e deslocamento a partir de 2,0.



Sucesso! Desta vez, o neurônio aprendeu rapidamente, como queríamos. Se você observar atentamente, poderá ver que a inclinação da curva de custo é inicialmente mais íngreme em comparação com a região plana da curva de valor quadrático correspondente. Essa entropia entre países nos dá essa frieza e não nos deixa presos onde esperamos o treinamento mais rápido de um neurônio quando ele começa com grandes erros.

Eu não disse que velocidade de treinamento foi usada nos últimos exemplos. Anteriormente, com um valor quadrático, usamos η = 0,15. Devemos usar a mesma velocidade nos novos exemplos? De fato, mudando a função de custo, é impossível dizer exatamente o que significa usar a "mesma" velocidade de aprendizado; será uma comparação de maçãs com laranjas. Para ambas as funções de custo, experimentei procurando uma velocidade de aprendizado que me permitisse ver o que está acontecendo. Se você ainda estiver interessado, nos exemplos mais recentes, η = 0,005.

Você pode argumentar que mudar a velocidade do aprendizado torna os gráficos sem sentido. Quem se importa com a rapidez com que um neurônio aprende se podemos escolher arbitrariamente uma velocidade de aprendizado? Mas essa objeção não leva em consideração o ponto principal. O significado dos gráficos não está na velocidade absoluta da aprendizagem, mas em como essa velocidade muda. Ao usar a função quadrática, o treinamento é mais lento se o neurônio estiver muito errado, e então vai mais rápido quando o neurônio se aproxima da resposta desejada. Com a entropia cruzada, o aprendizado é mais rápido quando um neurônio comete um grande erro. E essas declarações não dependem de uma determinada velocidade de aprendizado.

Examinamos entropia cruzada para um neurônio. No entanto, é fácil generalizar para redes com muitas camadas e muitos neurônios. Suponha que y = y ₁ , y ₂ , ... são os valores desejados dos neurônios de saída, ou seja, os neurônios da última camada, e um ^L ₁ , um ^L ₂ , ... são os próprios valores de saída. Então a entropia cruzada pode ser definida como:

$$

$$C = - \ frac {1} {n} \ sum_x \ sum_j \ left [y_j \ ln a ^ L_j + (1-y_j) \ ln (1-a ^ L_j) \ right] \ tag {63}$$

É o mesmo que a equação (57), só que agora nossa soma de todos os neurônios de saída. Não analisarei a derivada em detalhes, mas é razoável supor que, usando a expressão (63), possamos evitar a desaceleração nas redes com muitos neurônios. Se estiver interessado, você pode obter a derivada no problema abaixo.

Aliás, o termo “entropia cruzada” que eu uso confundiu alguns dos primeiros leitores do livro porque contradiz outras fontes. Em particular, frequentemente a entropia cruzada é determinada para duas distribuições de probabilidade, pj
e qj, como ∑ _j p _j lnq _j . Essa definição pode ser associada a (57), se um neurônio sigmóide for considerado como fornecendo uma distribuição de probabilidade que consiste na ativação dos valores dos neurônios ae 1-a complementares.

No entanto, se tivermos muitos neurônios sigmóides na última camada, o vetor a ^L _j geralmente não fornece uma distribuição de probabilidade. Como resultado, a definição do tipo ∑ _j p _j lnq _j não _tem sentido, pois não trabalhamos com distribuições de probabilidade. Em vez disso (63), pode-se imaginar como um conjunto resumido de entropias cruzadas de cada neurônio é resumido, onde a ativação de cada neurônio é interpretada como parte de uma distribuição de probabilidade de dois elementos (é claro, não há elementos de probabilidade em nossas redes, portanto, na verdade, não são probabilidades). Nesse sentido, (63) será uma generalização da entropia cruzada para distribuições de probabilidade.

Quando usar entropia cruzada em vez de valor quadrático? De fato, a entropia cruzada quase sempre será usada melhor se você tiver neurônios de saída sigmóide. Para entender isso, lembre-se de que, ao configurar uma rede, geralmente inicializamos pesos e compensações usando um processo aleatório. Pode acontecer que essa escolha leve ao fato de que a rede interpretará completamente alguns dados de entrada de treinamento - por exemplo, o neurônio de saída tenderá a 1, quando deve ir para 0 ou vice-versa. Se usarmos um valor quadrático que retarda o treinamento, ele não interromperá o treinamento, pois os pesos continuarão a ser treinados em outros exemplos de treinamento, mas essa situação é obviamente indesejável.

Exercícios

• Um problema da entropia cruzada é que, a princípio, pode ser difícil lembrar os papéis correspondentes de y e a. É fácil ficar confuso, como será correto, - [ylna + (1 - y) ln (1 - a)] ou - [alny + (1 - a) ln (1 - y)]. O que acontecerá com a segunda expressão quando y = 0 ou 1? Esse problema afeta a primeira expressão? Porque
• Na discussão de um único neurônio no início da seção, eu disse que a entropia cruzada é pequena se σ (z) yy para todos os dados de entrada do treinamento. , y 0 1. , (, ) y 0 1. , , σ(z)=y . ,

  $$

  $$C = -\frac{1}{n} \sum_x [y \ln y+(1-y) \ln(1-y)] \tag{64}$$
  . −[ylny+(1−y)ln(1−y)] .

• . ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \sigma'(z^L_j) \tag{65}$$
  σ'(z ^L _j ) , . , δ ^L x

  $$

  $$\delta^L = a^L-y \tag{66}$$
  , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{67}$$
  σ'(z ^L _j ) , , , . . , .
• . , . , , , , a ^L _j = z ^L _j . , δL x

  $$

  $$\delta^L = a^L-y \tag{68}$$
  , , , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{69}$$

  $$

  $$\frac{\partial C}{\partial b^L_{j}} = \frac{1}{n} \sum_x (a^L_j-y_j) \tag{70}$$
  , , . .

MNIST

A entropia cruzada é fácil de implementar como parte de um programa que ensina a rede usando descida de gradiente e propagação de retorno. Faremos isso mais tarde desenvolvendo uma versão aprimorada do nosso programa de classificação numérica manuscrita do MNIST, network.py. O novo programa é chamado network2.py e inclui não apenas entropia cruzada, mas também várias outras técnicas desenvolvidas neste capítulo. Enquanto isso, vamos ver o quão bem nosso novo programa classifica os dígitos MNIST. Como no capítulo 1, usaremos uma rede com 30 neurônios ocultos e um mini-pacote de tamanho 10. Definiremos a velocidade de aprendizado η = 0,5 e aprenderemos 30 eras.

Como eu já disse, é impossível dizer exatamente qual velocidade de treinamento é adequada e, nesse caso, experimentei a seleção. É verdade que existe uma maneira de relacionar heuristicamente a taxa de aprendizado com a entropia e o valor quadrático. Vimos anteriormente que, nos termos do gradiente para o valor quadrático, existe um termo adicional σ '= σ (1-σ). Suponha que calculemos a média desses valores para σ, ₀ ¹ ₀ dσ σ (1 - σ) = 1/6. Pode-se observar que o custo quadrático (aproximadamente) aprende, em média, 6 vezes mais devagar para a mesma taxa de aprendizado. Isso sugere que um bom ponto de partida seria dividir a velocidade de aprendizado de uma função quadrática por 6. É claro que esse não é um argumento estrito, e você não deve levar isso muito a sério. Mas às vezes pode ser útil como ponto de partida.

A interface do network2.py é um pouco diferente do network.py, mas ainda deve ficar claro o que está acontecendo. A documentação em network2.py pode ser obtida usando o comando help (network2.Network.SGD) no shell python.

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True) 

Observe, a propósito, que o comando net.large_weight_initializer () é usado para inicializar pesos e compensações da mesma maneira como descrito no capítulo 1. Precisamos executá-lo porque alteraremos a inicialização de pesos por padrão mais tarde. Como resultado, após iniciar todos os comandos acima, obtemos uma rede que funciona com uma precisão de 95,49%. Isso está muito próximo do resultado do primeiro capítulo, 95,42%, usando o valor quadrático.

Vejamos também o caso em que usamos 100 neurônios ocultos e entropia cruzada e deixamos o resto da mesma forma. Nesse caso, a precisão é de 96,82%. Essa é uma grande melhoria em relação aos resultados do primeiro capítulo, onde alcançamos uma precisão de 96,59% usando o valor quadrático. A alteração pode parecer pequena, mas pense que o erro caiu de 3,41% para 3,18%. Ou seja, eliminamos aproximadamente 1/14 dos erros. Isso é muito bom.

É muito bom que a função de custo de entropia cruzada nos dê resultados semelhantes ou melhores em comparação com o valor quadrático. No entanto, eles não provam inequivocamente que a entropia cruzada é a melhor escolha. O fato é que eu não tentei escolher os hiperparâmetros - a velocidade do treinamento, o tamanho da minipacote, etc. Para tornar a melhoria mais convincente, precisamos lidar adequadamente com a otimização. Mas os resultados ainda são inspiradores, e nossos cálculos teóricos confirmam que a entropia cruzada é uma escolha melhor do que a função de custo quadrático.

Nesse sentido, este capítulo inteiro e, em princípio, o restante do livro serão apresentados. Vamos desenvolver novas tecnologias, testá-las e obter "melhores resultados". Claro, é bom que vejamos essas melhorias. Mas interpretá-los é sempre difícil. Só será convincente se observarmos melhorias após um trabalho sério na otimização de todos os outros hiperparâmetros. E esse é um trabalho bastante complicado, que requer grandes recursos computacionais, e geralmente não lidaremos com uma investigação tão completa. Em vez disso, iremos além com base em testes informais, como os listados acima. Mas você deve ter em mente que esses testes não são evidências inequívocas e monitorar cuidadosamente esses casos quando os argumentos começarem a falhar.

Até agora, discutimos a entropia cruzada em detalhes. Por que desperdiçar tanto esforço se isso oferece uma melhoria tão pequena em nossos resultados do MNIST? Mais adiante neste capítulo, veremos outras técnicas - em particular a regularização - que oferecem melhorias muito mais fortes. Então, por que nos concentramos na entropia cruzada? Em particular, como a entropia cruzada é uma função de valor usada com frequência, vale a pena entender bem. Mas a razão mais importante é que a saturação dos neurônios é um problema importante no campo das redes neurais, ao qual retornaremos constantemente ao longo do livro. Portanto, discuti a entropia cruzada com tanto detalhe, pois é um bom laboratório começar a entender a saturação dos neurônios e como abordar abordagens para esse problema.

O que significa entropia cruzada? De onde vem?

Nossa discussão sobre entropia cruzada girou em torno da análise algébrica e da implementação prática. Isso é útil, mas, como resultado, questões conceituais mais amplas permanecem sem resposta, por exemplo: o que significa entropia cruzada? Existe uma maneira intuitiva de apresentá-lo? Como as pessoas poderiam sugerir entropia cruzada?

Vamos começar com o último: o que poderia nos fazer pensar em entropia cruzada? Suponha que descobrimos uma desaceleração do aprendizado descrita anteriormente e percebemos que ela foi causada pelos termos σ '(z) nas equações (55) e (56). Olhando de relance para essas equações, poderíamos pensar se é possível escolher uma função de custo para que o termo σ '(z) desapareça. Então o custo C = C _{x de} um exemplo de treinamento satisfaria as equações:

$$

$$\ frac {\ parcial C} {\ parcial w_j} = x_j (a-y) \ tag {71}$$

$$

$$\ frac {\ parcial C} {\ parcial b} = (a-y) \ tag {72}$$

Se escolhermos uma função de valor que os torne verdadeiros, eles prefeririam simplesmente descrever um entendimento intuitivo de que quanto maior o erro inicial, mais rápido o neurônio aprende. Eles também resolveriam o problema de desaceleração. De fato, começando com essas equações, mostraríamos que é possível derivar a forma de entropia cruzada simplesmente seguindo um instinto matemático. Para ver isso, observamos que, com base na regra da cadeia, obtemos:

$$

$$\ frac {\ parcial C} {\ parcial b} = \ frac {\ parcial C} {\ parcial a} \ sigma '(z) \ tag {73}$$

Usando na última equação σ ′ (z) = σ (z) (1 - σ (z)) = a (1 - a), obtemos:

$$

$$\ frac {\ parcial C} {\ parcial b} = \ frac {\ parcial C} {\ parcial a} a (1-a) \ tag {74}$$

Comparando com a equação (72), obtemos:

$$

$$\ frac {\ parcial C} {\ parcial a} = \ frac {a-y} {a (1-a)} \ tag {75}$$

Integrando esta expressão sobre a, obtemos:

$$

$$C = - [y \ ln a + (1-y) \ ln (1-a)] + {\ rm constante} \ tag {76}$$

Essa é a contribuição de um exemplo de treinamento separado x para a função de custo. Para obter a função de custo total, precisamos calcular a média de todos os exemplos de treinamento e chegamos a:

$$

$$C = - \ frac {1} {n} \ sum_x [y \ n em + (1-y) \ ln (1-a)] + {\ rm constante} \ tag {77}$$

A constante aqui é a média das constantes individuais de cada um dos exemplos de treinamento. Como você pode ver, as equações (71) e (72) determinam exclusivamente a forma da entropia cruzada, carne para uma constante comum. A entropia cruzada não foi magicamente retirada do ar. Ela poderia ser encontrada de uma maneira simples e natural.

E a idéia intuitiva de entropia cruzada? Como imaginamos isso? Uma explicação detalhada nos levaria a superar nosso curso de treinamento. No entanto, podemos mencionar a existência de uma maneira padrão de interpretar entropia cruzada, originada no campo da teoria da informação. Grosso modo, a entropia cruzada é uma surpresa. Por exemplo, nosso neurônio está tentando calcular a função x → y = y (x). Mas, em vez disso, conta a função x → a = a (x). Suponha que imaginemos a estimativa de um neurônio da probabilidade de que y = 1 e 1-a é a probabilidade de que o valor correto para y seja 0. Então a entropia cruzada mede o quanto estamos "surpresos", em média, quando encontre o verdadeiro valor de y. Não ficamos surpresos se esperamos uma saída, e ficamos surpresos se a saída for inesperada. Claro, eu não dei uma definição estrita de "surpresa", então tudo isso pode parecer discurso retórico. Mas, de fato, na teoria da informação, existe uma maneira exata de determinar o inesperado. Infelizmente, não conheço nenhum exemplo de uma discussão boa, curta e auto-suficiente sobre esse ponto na Internet. Mas se você estiver interessado em aprofundar um pouco mais, o artigo da Wikipedia possui boas informações gerais que o enviarão na direção certa. Detalhes podem ser encontrados no Capítulo 5, sobre desigualdade Kraft, em um livro sobre teoria da informação .

Desafio

• Discutimos em detalhes a desaceleração no aprendizado que pode ocorrer quando os neurônios estão saturados em redes usando a função de custo quadrático no aprendizado. Outro fator que pode inibir a aprendizagem é a presença do termo x _j na equação (61). Por isso, quando a saída x _{j se} aproxima de zero, o peso correspondente w _j será treinado lentamente. Explique por que é impossível eliminar o termo x _j escolhendo alguma função de custo engenhosa.

Softmax (função máxima suave)

Neste capítulo, usaremos principalmente a função de custo de entropia cruzada para resolver os problemas de desaceleração do aprendizado. No entanto, gostaria de discutir brevemente outra abordagem para esse problema, com base no chamado softmax-camadas de neurônios. Não usaremos as camadas Softmax no restante deste capítulo; portanto, se você estiver com pressa, poderá pular esta seção. No entanto, o Softmax ainda vale a pena entender, em particular porque é interessante por si só, e em particular porque usaremos as camadas do Softmax no Capítulo 6, em nossa discussão sobre redes neurais profundas.

A idéia do Softmax é definir um novo tipo de camada de saída para HC. Começa da mesma maneira que a camada sigmóide, com a formação de insumos ponderados $$$z ^ L_j = \ sum_ {k} w ^ L_ {jk} a ^ {L-1} _k + b ^ L_j$ . No entanto, não usamos um sigmóide para obter uma resposta. Na camada Softmax, aplicamos a função Softmax a z ^L _j . Segundo ela, a ativação a ^L _{j do} neurônio de saída n. J é igual a:

$$

$$a ^ L_j = \ frac {e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} \ tag {78}$$

onde no denominador somamos todos os neurônios de saída.

Se a função Softmax não lhe é familiar, a equação (78) parecerá misteriosa para você. Não é de todo óbvio por que devemos usar essa função. Também não é óbvio que isso nos ajudará a resolver o problema de desacelerar o aprendizado. Para entender melhor a equação (78), suponha que tenhamos uma rede com quatro neurônios de saída e quatro entradas ponderadas correspondentes, que designaremos como z ^L ₁ , z ^L ₂ , z ^L ₃ e z ^L ₄ . O artigo original contém controles deslizantes interativos, aos quais são atribuídos os possíveis valores das entradas ponderadas e o cronograma das ativações de saída correspondentes. Um bom ponto de partida para estudá-los seria usar o controle deslizante inferior para aumentar z ^L ₄ .





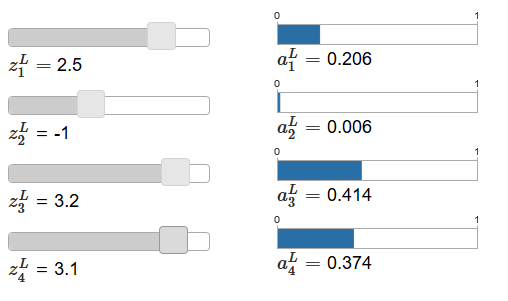
Ao aumentar z ^L ₄ , pode-se observar um aumento na ativação de saída correspondente, um ^L ₄ e uma diminuição em outras ativações de saída. Com a diminuição de z ^L _4, a ^L ₄ diminuirá e todas as outras ativações de saída aumentarão. Observando atentamente, você verá que, nos dois casos, a mudança geral em outras ativações compensa exatamente a mudança que ocorre em um ^L ₄ . A razão para isso é a garantia de que todas as ativações de saída no total dão 1, o que podemos provar usando a equação (78) e alguma álgebra:

$$

$$\ sum_j a ^ L_j = \ frac {\ sum_j e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} = 1 \ tag {79}$$

Como resultado, com um aumento em um ^L _{4, as} ativações de saída restantes devem diminuir no mesmo valor no total para garantir que a soma de todas as ativações de saída seja igual a 1. E, é claro, declarações semelhantes serão verdadeiras para todas as outras ativações.

Também resulta da equação (78) que todas as ativações de saída são positivas, uma vez que a função exponencial é positiva. Combinando isso com a observação do parágrafo anterior, descobrimos que a saída da camada Softmax será um conjunto de números positivos, totalizando 1. Em outras palavras, a saída da camada Softmax pode ser representada como uma distribuição de probabilidade.

O fato de a saída da camada Softmax ser uma distribuição de probabilidade é muito agradável. Em muitos problemas, é conveniente poder interpretar as ativações de saída a ^L _j como uma estimativa da rede da probabilidade de que o bulet j seja a opção correta. Assim, por exemplo, no problema de classificação MNIST, podemos interpretar um ^L _j como uma estimativa pela rede da probabilidade de que j será a versão correta da classificação de um dígito.

Por outro lado, se a camada de saída era sigmóide, então definitivamente não podemos assumir que as ativações formam uma distribuição de probabilidade. Não vou provar isso estritamente, mas é razoável supor que as ativações da camada sigmóide no caso geral não formam uma distribuição de probabilidade. Portanto, usando uma camada de saída sigmóide, não teremos uma interpretação tão simples das ativações de saída.

Exercício

• Faça um exemplo mostrando que em uma rede com uma camada de saída sigmóide, as ativações de saída a ^L _j nem sempre somam 1.

Começamos a entender um pouco sobre as funções da Softmax e como as camadas da Softmax se comportam. Apenas para resumir: os expoentes na equação (78) garantem que todas as ativações de saída sejam positivas. A soma no denominador da equação (78) garante que a Softmax dê um total de 1. Portanto, esse tipo de equação não parece mais misterioso: é uma maneira natural de garantir que as ativações de saída formem uma distribuição de probabilidade. O Softmax pode ser imaginado como uma maneira de escalar z ^L _j e depois compactá-los para formar uma distribuição de probabilidade.

Exercícios

• A monotonia do Softmax. Mostre que La ^L _j / ∂z ^L _{k é} positivo se j = k e negativo se j ≠ k. Como resultado, _é garantido um aumento em z ^L _j para aumentar a ativação de saída correspondente a ^L _j e diminui todas as outras ativações de saída. Já vimos isso empiricamente usando o exemplo de controles deslizantes, mas essa prova será rigorosa.
• Não localidade Softmax. Uma característica interessante das camadas sigmóides é que a saída a ^L _j é uma função da entrada ponderada correspondente, a ^L _j = σ (z ^L _j ). Explique por que esse não é o caso da camada Softmax: qualquer ativação de saída a ^L _j depende de todas as entradas ponderadas.

Desafio

• Inverta a camada Softmax. Suponha que temos um NS com uma camada Softmax de saída e as ativações a ^L _{j são} conhecidas. Mostre que as entradas ponderadas correspondentes têm a forma z ^L _j = ln a ^L _j + C, onde C é uma constante independente de j.

Problema de desaceleração da aprendizagem

Já nos familiarizamos bastante com as camadas de neurônios Softmax. Mas até agora não vimos como as camadas Softmax nos permitem resolver o problema de desacelerar o aprendizado. Para entender isso, vamos definir uma função de custo com base na "probabilidade de log". Usaremos x para indicar a entrada de treinamento da rede e y para a saída desejada correspondente. O LPS associado a esta entrada de treinamento será:

$$

$$C \ equiv - \ em um ^ L_y \ tag {80}$$

Portanto, se, por exemplo, estudarmos imagens MNIST, e a imagem 7 for inserida na entrada, o LPS será - em um ^L ₇ . Para entender isso intuitivamente, consideramos o caso em que a rede lida bem com o reconhecimento, ou seja, é certo que está na entrada 7. Nesse caso, ele avaliará o valor da probabilidade correspondente a ^L ₇ como próximo de 1, portanto, o custo - em um ^L ₇ será pequeno . Por outro lado, se a rede não funcionar bem, a probabilidade de um ^L7 será menor e o custo - em um L7 será maior. Portanto, o LPS se comporta conforme o esperado de uma função de custo.

E o problema da desaceleração? Para analisá-lo, lembramos que o principal na desaceleração é o comportamento de ∂C / ∂w ^L _jk e ∂C / ∂b ^L _j . Não descreverei em detalhes a captura da derivada - pedirei que você faça isso em tarefas, mas usando alguma álgebra, você pode mostrar que:

$$

$$\ frac {\ parcial C} {\ parcial b ^ L_j} = a ^ L_j-y_j \ tag {81}$$

$$

$$\ frac {\ parcial C} {\ parcial w ^ L_ {jk}} = a ^ {L-1} _k (a ^ L_j-y_j) \ tag {82}$$

Eu brinquei um pouco com a notação aqui e estou usando "y" um pouco diferente do que no último parágrafo. Lá, y denota a saída de rede desejada - ou seja, se a saída for “7”, a entrada será a imagem 7. E nessas equações, y denota o vetor de ativação de saída correspondente a 7, ou seja, um vetor com todos os zeros, exceto a unidade em 7 posição.

Essas equações são iguais às expressões semelhantes que obtivemos em uma análise anterior da entropia cruzada. Compare, por exemplo, as equações (82) e (67). Essa é a mesma equação, embora a última seja calculada sobre os exemplos de treinamento. E, como no primeiro caso, essas expressões garantem que o aprendizado não seja mais lento. É útil imaginar que a camada Softmax de saída com LPS é bastante semelhante à camada com saída sigmóide e custo com base na entropia cruzada.

Dada sua semelhança, o que deve ser usado - saída sigmóide e entropia cruzada, ou saída Softmax e LPS? De fato, em muitos casos, ambas as abordagens funcionam bem. Embora mais adiante neste capítulo, usaremos uma camada de saída sigmóide com um custo baseado na entropia cruzada. Mais tarde, no capítulo 6, às vezes usaremos a saída Softmax e o LPS. O motivo das mudanças é tornar algumas das redes a seguir mais semelhantes às redes encontradas em alguns artigos de pesquisa influentes. De um ponto de vista mais geral, o Softmax e o LPS devem ser usados ​​quando você precisar interpretar as ativações de saída como probabilidades. Isso nem sempre é necessário, mas pode ser útil em problemas de classificação (como MNIST), que incluem classes sem interseção.

As tarefas

• Derive as equações (81) e (82).
• De onde vem o nome Softmax? Suponha que alteremos a função Softmax para que as ativações de saída sejam dadas pela equação

  $$

  $$a ^ L_j = \ frac {e ^ {c z ^ L_j}} {\ sum_k e ^ {c z ^ L_k}} \ tag {83}$$
  onde c é uma constante positiva. Observe que c = 1 corresponde à função padrão Softmax. Mas, usando um valor diferente de c, obtemos outra função que ainda será qualitativamente semelhante à Softmax. Mostre que as ativações de saída formam uma distribuição de probabilidade, como é o caso do Softmax regular. Suponha que façamos c muito grande, ou seja, c → & inf; Qual é o valor limite das ativações de saída a ^L _j ? Depois de resolver esse problema, deve ficar claro por que uma função com c = 1 é considerada uma "versão suavizada" da função máxima. É daí que vem o termo softmax.
• Propagação traseira com Softmax e LPS. No último capítulo, derivamos o algoritmo de retropropagação para uma rede contendo camadas sigmóides. Para aplicar esse algoritmo às camadas de rede e Softmax, precisamos derivar a expressão para o erro δ ^L _j ≡ C / ∂z ^L _j . Mostre que uma expressão adequada seria

  $$

  $$\ delta ^ L_j = a ^ L_j -y_j \ tag {84}$$
  Usando essa expressão, podemos aplicar o algoritmo de retropropagação à rede usando a camada Softmax de saída e o LPS.

Reciclagem e regularização

O ganhador do Nobel, Enrico Fermi, já foi convidado a opinar sobre o modelo matemático proposto por vários colegas para resolver um importante problema físico não resolvido. O modelo correspondia perfeitamente ao experimento, mas Fermi estava cético quanto a isso. Ele perguntou quantos parâmetros livres podem ser alterados. "Quatro", eles disseram a ele. Fermi respondeu: "Lembro como meu amigo Johnny von Neumann gostava de dizer que, com quatro parâmetros, você pode empurrar um elefante para lá e, com cinco, você pode fazê-lo balançar a tromba".

O significado da história, é claro, é que modelos com um grande número de parâmetros livres podem descrever uma gama surpreendentemente ampla de fenômenos.Mesmo se esse modelo funcionar bem com os dados disponíveis, ele não será automaticamente um bom modelo. Apenas pode significar que o modelo tem liberdade suficiente para descrever quase todos os conjuntos de dados de um determinado tamanho sem revelar a idéia principal do fenômeno. Quando isso acontece, o modelo funciona bem com os dados existentes, mas não pode generalizar a nova situação. Um verdadeiro teste de um modelo é sua capacidade de fazer previsões em situações que ele não havia encontrado antes.

Fermi e von Neumann suspeitaram de modelos com quatro parâmetros. Nosso NS com 30 neurônios ocultos para a classificação dos dígitos MNIST possui quase 24.000 parâmetros! Estes são alguns parâmetros. Nosso NS com 100 neurônios ocultos tem quase 80.000 parâmetros, e os NSs avançados avançados desses parâmetros às vezes têm milhões ou até bilhões. Podemos confiar nos resultados de seu trabalho?

Vamos complicar esse problema criando uma situação em que nossa rede generaliza mal uma nova situação para ele. Usaremos NS com 30 neurônios ocultos e 23.860 parâmetros. Mas não treinaremos a rede com todas as 50.000 imagens MNIST. Em vez disso, usamos apenas os primeiros 1000. O uso de um conjunto limitado tornará o problema de generalização mais óbvio. Estudaremos como antes, usando a função de custo baseada na entropia cruzada, com uma velocidade de aprendizado de η = 0,5 e um tamanho de minipacote de 10. No entanto, estudaremos 400 eras, o que é um pouco mais do que antes, pois existem exemplos de treinamento não temos muito. Vamos usar o network2 para ver como a função de custo muda:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True, monitor_training_cost=True) 

Usando os resultados, podemos construir um gráfico da mudança de custo ao treinar a rede (os gráficos foram feitos usando o programa overfitting.py):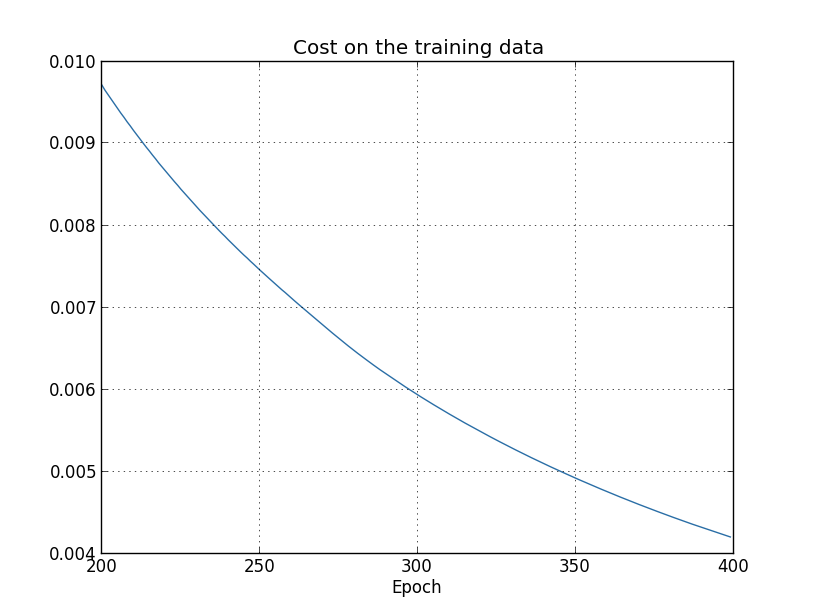



Parece encorajador, há uma redução suave no custo, conforme o esperado. Lembre-se de que mostrei apenas as épocas de 200 a 399. Como resultado, vemos em escala ampliada os estágios finais do treinamento, nos quais, como veremos mais adiante, tudo de mais interessante acontece.

Agora vamos ver como a precisão da classificação nos dados de verificação muda com o tempo:



Então eu novamente aumentei o cronograma. Nas primeiras 200 eras, que não são visíveis aqui, a precisão aumenta para quase 82%. Então o treinamento diminui gradualmente. Finalmente, por volta da era 280, a precisão da classificação cessa de melhorar. Em épocas posteriores, apenas pequenas flutuações estocásticas são observadas em torno do valor de precisão alcançado na 280ª época. Compare isso com o gráfico anterior, onde o custo associado aos dados de treinamento está diminuindo gradualmente. Se você estudar apenas esse custo, parecerá que o modelo está melhorando. No entanto, os resultados do trabalho com dados de teste nos dizem que essa melhoria é apenas uma ilusão. Como no modelo que Fermi não gostou, o que nossa rede estuda após a era 280 não é mais generalizado para dados de verificação. Portanto, esse treinamento deixa de ser útil. Dizemos que, após a era 280, a rede está se recuperando,ou sobreajuste.

Você pode estar se perguntando se não estou estudando o custo com base nos dados de treinamento e não na precisão da classificação dos dados de verificação. Em outras palavras, talvez o problema seja que estamos comparando maçãs com laranjas. O que acontecerá se compararmos o custo dos dados de treinamento com o custo da verificação, ou seja, compararemos medidas comparáveis? Ou talvez pudéssemos comparar a precisão da classificação dos dados de treinamento e teste? De fato, o mesmo fenômeno aparece independentemente de como a comparação é feita. Mas os detalhes estão mudando. Por exemplo, vamos ver o valor dos dados de verificação:



Pode-se observar que o custo dos dados de verificação melhora até a era 15 e depois começa a se deteriorar completamente, embora o custo dos dados de treinamento continue a melhorar. Este é outro sinal de um modelo reciclado. No entanto, surge a questão: em que época devemos considerar o ponto em que o treinamento começa a prevalecer sobre o treinamento - 15 ou 280? Do ponto de vista prático, estamos interessados ​​em melhorar a precisão da classificação dos dados de verificação, e o custo é apenas um mediador da precisão da classificação. Portanto, faz sentido considerar a era de 280 um ponto, após o qual a reciclagem começa a prevalecer sobre o treinamento de nossa Assembléia Nacional.

Outro sinal de reciclagem pode ser visto na precisão da classificação dos dados de treinamento:



A precisão está crescendo, chegando a 100%. Ou seja, nossa rede classifica corretamente todas as 1000 imagens de treinamento! Enquanto isso, a precisão da verificação aumenta para apenas 82,27%. Ou seja, nossa rede estuda apenas os recursos do conjunto de treinamento e não aprende a reconhecer números. Parece que a rede simplesmente se lembra do conjunto de treinamento, não entendendo os números suficientemente bem para generalizar isso para o conjunto de testes.

A reciclagem é um problema sério da Assembléia Nacional. Isso é especialmente verdadeiro para os NSs modernos, que geralmente têm uma enorme quantidade de pesos e deslocamentos. Para um treinamento eficaz, precisamos de uma maneira de determinar quando o treinamento ocorre para não ser treinado novamente. E também gostaríamos de poder reduzir os efeitos da reciclagem.

Uma maneira óbvia de detectar reciclagem é usar a abordagem acima, monitorar a precisão do trabalho com dados de verificação durante o treinamento em rede. Se percebermos que a precisão dos dados de verificação não está mais melhorando, devemos interromper o treinamento. Obviamente, estritamente falando, isso não será necessariamente um sinal de reciclagem. Talvez a precisão de trabalhar com dados de teste e treinamento pare de melhorar ao mesmo tempo. No entanto, a aplicação dessa estratégia impedirá a reciclagem.

E usaremos uma pequena variação dessa estratégia. Lembre-se de que quando carregamos dados no MNIST, os dividimos em três conjuntos:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Até agora, usamos training_data e test_data, e ignoramos validation_data [confirmando]. Os dados de validação contêm 10.000 imagens, que diferem das 50.000 imagens do conjunto de treinamento MNIST e das 10.000 imagens do conjunto de validação. Em vez de usar test_data para evitar overfitting, usaremos validation_data. Para fazer isso, usaremos quase a mesma estratégia descrita acima para test_data. Ou seja, calcularemos a precisão da classificação de validation_data no final de cada época. Quando a precisão da classificação de validation_data estiver cheia, deixaremos de aprender. Essa estratégia é chamada de parada antecipada. Obviamente, na prática, não seremos capazes de descobrir imediatamente que a precisão está saciada. Em vez disso, continuaremos treinando até ter certeza disso (e decidirquando você precisa parar, nem sempre é fácil, e você pode usar abordagens mais ou menos agressivas para isso).

Por que usar validation_data para impedir a reciclagem em vez de test_data? Faz parte de uma estratégia mais geral o uso de validation_data para avaliar diferentes opções de hiperparâmetros - o número de épocas para aprender, a velocidade do aprendizado, a melhor arquitetura de rede etc. Usamos essas estimativas para encontrar e atribuir bons valores aos hiperparâmetros. E, embora ainda não tenha mencionado isso, foi em parte por isso que fiz a escolha de hiperparâmetros nos exemplos anteriores do livro.

Obviamente, essa observação não responde à pergunta de por que usamos validation_data, e não test_data, para evitar o super ajuste. Simplesmente substitui a resposta a uma pergunta mais geral - por que usamos validation_data, e não test_data, para selecionar hiperparâmetros? Para entender isso, lembre-se de que, ao escolher hiperparâmetros, é provável que tenhamos que escolher entre uma variedade de opções. Se atribuirmos hiperparâmetros com base nas classificações de test_data, provavelmente adaptaremos esses dados muito especificamente para test_data. Ou seja, podemos encontrar hiperparâmetros adequados aos recursos específicos de dados específicos de test_data; no entanto, a operação de nossa rede não será generalizada para outros conjuntos de dados. Evitamos isso selecionando hiperparâmetros usando validation_data. E então, tendo recebido o GP, precisamos,realizamos uma avaliação final da precisão usando test_data. Isso nos dá confiança de que nossos resultados com test_data são uma verdadeira medida do grau de generalização do NS. Em outras palavras, dados de suporte são dados de treinamento especiais que nos ajudam a aprender um bom GP. Essa abordagem para localizar GPs às vezes é chamada de método de retenção, pois validation_data é "mantido" separadamente do training_data.

Na prática, mesmo depois de avaliar a qualidade do trabalho em test_data, queremos mudar de idéia e tentar uma abordagem diferente - talvez uma arquitetura de rede diferente - que inclua buscas por um novo conjunto de GPs. Nesse caso, existe o perigo de nos adaptarmos desnecessariamente ao test_data? Precisamos de um número potencialmente infinito de conjuntos de dados para garantir que nossos resultados sejam bem generalizados? Em geral, esse é um problema profundo e complexo. Mas, para nossos propósitos práticos, não nos preocuparemos muito com isso. Simplesmente nos aprofundamos em pesquisas adicionais usando um método simples de retenção baseado em training_data, validation_data e test_data, conforme descrito acima.

Até agora, consideramos a reciclagem usando 1000 imagens de treinamento. O que acontece se usarmos um conjunto completo de treinamento de 50.000 imagens? Vamos deixar todos os outros parâmetros inalterados (30 neurônios ocultos, velocidade de aprendizado 0,5, tamanho de minipacote 10), mas estudaremos 30 épocas usando todas as 50.000 imagens. Aqui está um gráfico que mostra a precisão da classificação nos dados de treinamento e teste. Observe que aqui eu usei dados de validação em vez de dados de validação para facilitar a comparação dos resultados com gráficos anteriores.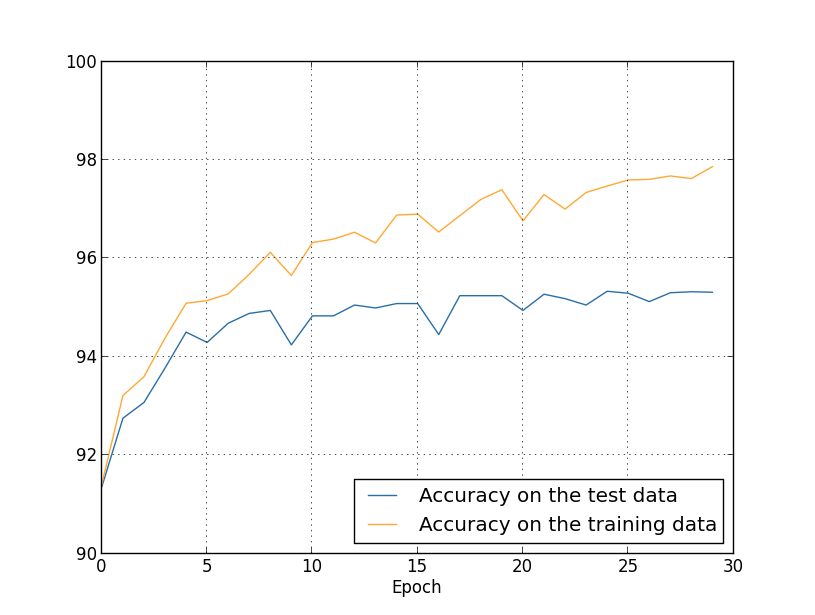



Pode-se observar que os indicadores de precisão nos dados de teste e treinamento permanecem mais próximos um do outro do que quando se usam 1000 exemplos de treinamento. Em particular, a melhor precisão de classificação, 97,86%, é apenas 2,53% superior a 95,33% dos dados de verificação. Compare com uma pausa precoce de 17,73%! A reciclagem está ocorrendo, mas é bastante reduzida. Nossa rede compila informações muito melhor, passando do treinamento para os dados de teste. Em geral, uma das melhores maneiras de reduzir a reciclagem é aumentar a quantidade de dados de treinamento. Com dados de treinamento suficientes, é difícil treinar até mesmo uma rede muito grande. Infelizmente, obter dados de treinamento é caro e / ou difícil, portanto, essa opção nem sempre é prática.

Regularização

Aumentar a quantidade de dados de treinamento é uma maneira de reduzir a reciclagem. Existem outras maneiras de reduzir a reciclagem? Uma abordagem possível é reduzir o tamanho da rede. É verdade que as redes grandes têm potencial mais do que as pequenas, por isso estamos relutantes em recorrer a essa opção.

Felizmente, existem outras técnicas que podem reduzir a reciclagem, mesmo quando corrigimos o tamanho da rede e dos dados de treinamento. Eles são conhecidos como técnicas de regularização. Neste capítulo, descreverei uma das técnicas mais populares, às vezes chamadas de enfraquecimento de pesos ou regularização de L2. Sua ideia é adicionar um membro extra chamado membro de regularização à função de custo. Aqui está a entropia cruzada com regularização:

$$

$$C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2 \tag{85}$$

O primeiro termo é uma expressão comum para entropia cruzada. Mas adicionamos um segundo, a soma dos quadrados de todos os pesos da rede. É dimensionado pelo fator λ / 2n, onde λ> 0 é o parâmetro de regularização e n, como de costume, é o tamanho do conjunto de treinamento. Discutiremos como escolher λ. Também é importante notar que os vieses não estão incluídos no termo de regularização. Sobre isso abaixo.

Obviamente, é possível regularizar outras funções de custo, por exemplo, quadráticas. Isso pode ser feito de maneira semelhante:

$$

$$C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2 \tag{86}$$

Nos dois casos, podemos escrever a função de custo regularizado como

$$

$$C = C_0 + \frac{\lambda}{2n} \sum_w w^2 \tag{87}$$

onde C ₀ é a função de custo original sem regularização.

É intuitivamente claro que o objetivo da regularização é convencer a rede a preferir pesos menores, todas as outras coisas sendo iguais. Pesos grandes só serão possíveis se eles melhorarem significativamente a primeira parte da função de custo. Em outras palavras, a regularização é uma maneira de escolher um compromisso entre encontrar pesos pequenos e minimizar a função de custo inicial. É importante que esses dois elementos do compromisso dependam do valor de λ: quando λ é pequeno, preferimos minimizar a função de custo original e, quando λ é grande, preferimos pesos pequenos.

Não é de todo óbvio por que a escolha de tal compromisso deve ajudar a reduzir a reciclagem! Mas acontece que ajuda. Vamos descobrir por que isso ajuda na próxima seção. Mas primeiro, vamos trabalhar com um exemplo mostrando que a regularização reduz a reciclagem.

Para construir um exemplo, primeiro precisamos entender como aplicar o algoritmo de treinamento com descida de gradiente estocástico a um NS regularizado. Em particular, precisamos saber como calcular as derivadas parciais, ∂C / ∂w e ∂C / ∂b para todos os pesos e compensações na rede. Depois de tomar as derivadas parciais na equação (87), obtemos:

$$

$$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}$$

$$

$$\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b} \tag{89}$$

Os termos ∂C ₀ / ∂w e ∂C ₀ / ∂w podem ser calculados através do OP, conforme descrito no capítulo anterior. Vimos que é fácil calcular o gradiente da função de custo regularizado: você só precisa usar o OP como de costume e adicionar λ / nw à derivada parcial de todos os termos de peso. As derivadas parciais em relação aos deslocamentos não mudam, portanto, a regra do aprendizado por descida gradiente para deslocamentos não difere da usual:

$$

$$b \rightarrow b -\eta \frac{\partial C_0}{\partial b} \tag{90}$$

A regra de treinamento para pesos se transforma em:

$$

$$w \rightarrow w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}$$

$$

$$= \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w} \tag{92}$$

Tudo é o mesmo da regra de descida de gradiente usual, exceto que primeiro escalamos o peso w por um fator de 1 - ηλ / n. Esse dimensionamento às vezes é chamado de perda de peso, pois reduz o peso. À primeira vista, parece que os pesos estão irresistivelmente tendendo a zero. Mas não é assim, já que o outro termo pode levar a um aumento de peso se isso levar a uma diminuição na função de custo irregular.

Ok, deixe a descida gradiente funcionar assim. E quanto à descida do gradiente estocástico? Bem, como na versão irregular da descida do gradiente estocástico, podemos estimar ∂C ₀ / ∂w através da média do mini-pacote de m exemplos de treinamento. Portanto, a regra de aprendizado regularizado para a descida do gradiente estocástico se transforma (veja a equação (20)):

$$

$$w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w} \tag{93}$$

onde a soma vale para os exemplos de treinamento x no minipacote e C _x é o custo irregular de cada exemplo de treinamento. Tudo é o mesmo da regra usual da descida do gradiente estocástico, com exceção de 1 - ηλ / n, o fator de perda de peso. Por fim, para concluir a imagem, deixe-me escrever uma regra regularizada para compensações. Naturalmente, é exatamente o mesmo que no caso irregular (veja a equação (21)):

$$

$$b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b} \tag{94}$$

onde o valor vale para os exemplos de treinamento x no minipacote.

Vamos ver como a regularização muda a eficácia de nossa Assembléia Nacional. Usaremos uma rede com 30 neurônios ocultos, um mini-pacote de tamanho 10, uma velocidade de aprendizado de 0,5 e uma função de custo com entropia cruzada. No entanto, desta vez, usamos o parâmetro de regularização λ = 0,1. No código, chamei essa variável de lmbda, pois a palavra lambda é reservada em python para coisas não relacionadas ao nosso tópico. Também usei test_data novamente em vez de validation_data. Mas eu decidi usar test_data, porque os resultados podem ser comparados diretamente com nossos resultados irregulares. Você pode alterar facilmente o código para que ele use validation_data e verifique se os resultados são semelhantes.

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, ... evaluation_data=test_data, lmbda = 0.1, ... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, ... monitor_training_cost=True, monitor_training_accuracy=True) 

O custo dos dados de treinamento está diminuindo constantemente, como no caso anterior, sem regularização:



mas desta vez, a precisão em test_data continua aumentando em todas as 400 épocas: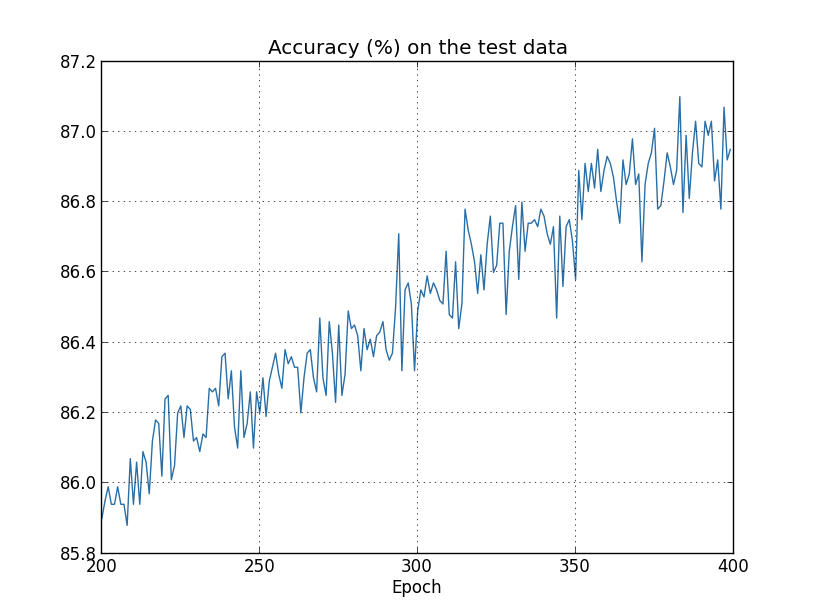



Obviamente, a regularização suprimiu a reciclagem. Além disso, a precisão aumentou significativamente e a precisão da classificação de pico atinge 87,1%, em comparação com o pico de 82,27% alcançado no caso sem regularização. Em geral, quase certamente alcançamos melhores resultados ao continuar estudando após 400 eras. Empiricamente, a regularização parece tornar nossa rede melhor generalizar o conhecimento e reduzir significativamente os efeitos da reciclagem.

O que acontece se deixarmos nosso ambiente artificial, que usa apenas 1.000 fotos de ensino, e retornarmos ao conjunto completo de 50.000 imagens? Obviamente, já vimos que a reciclagem é um problema muito menor, com um conjunto completo de 50.000 imagens. A regularização ajuda a melhorar o resultado? Vamos manter os valores anteriores dos hiperparâmetros - 30 épocas, velocidade 0,5, tamanho de minipacote 10. No entanto, precisamos alterar o parâmetro de regularização. O fato é que o tamanho n do conjunto de treinamento saltou de 1000 para 50 000, e isso altera o fator de enfraquecimento dos pesos 1 - ηλ / n. Se continuarmos a usar λ = 0,1, isso significa que os pesos são enfraquecidos muito menos e, como resultado, o efeito da regularização diminui. Nós compensamos isso aceitando λ = 5.0.

Ok, vamos treinar nossa rede reinicializando primeiro os pesos:

 >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, ... evaluation_data=test_data, lmbda = 5.0, ... monitor_evaluation_accuracy=True, monitor_training_accuracy=True) 

Temos os resultados: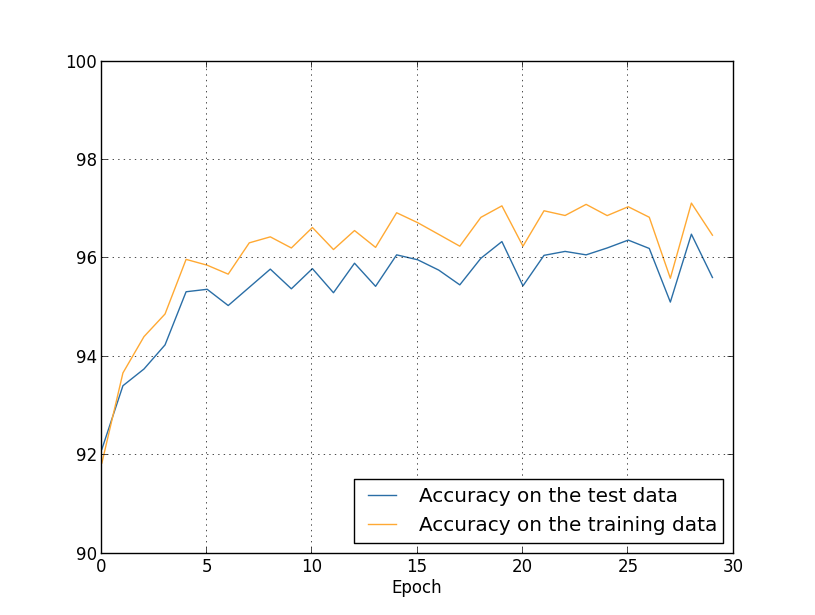



muitas coisas agradáveis. Em primeiro lugar, nossa precisão de classificação nos dados de verificação aumentou de 95,49% sem regularização para 96,49% com regularização. Esta é uma grande melhoria. Em segundo lugar, pode-se ver que a diferença entre os resultados do trabalho nos conjuntos de treinamento e teste é muito menor do que antes, menor que 1%. A diferença ainda é decente, mas obviamente fizemos progressos significativos na redução da reciclagem.

Por fim, veja qual precisão de classificação obtemos ao usar 100 neurônios ocultos e o parâmetro de regularização & lambda = 5.0. Não darei uma análise detalhada da reciclagem, isso é apenas diversão, para ver quanta precisão pode ser alcançada com nossos novos truques: uma função de custo com entropia cruzada e regularização de L2.

 >>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

O resultado final é uma precisão de classificação de 97,92% nos dados de suporte. Um grande salto em comparação com o caso de 30 neurônios ocultos. Você pode ajustar um pouco mais, iniciar o processo por 60 épocas com η = 0,1 e λ = 5,0 e superar a barreira de 98%, atingindo uma precisão de 98,04 nos dados de suporte. Nada mal para 152 linhas de código!

Descrevi a regularização como uma maneira de reduzir a reciclagem e aumentar a precisão da classificação. Mas essas não são suas únicas vantagens. Empiricamente, depois de tentar através de muitos lançamentos nossa rede MNIST, alterando pesos a cada vez, descobri que lançamentos sem regularização às vezes "ficavam presos", obviamente, caindo no mínimo local da função de custo. Como resultado, lançamentos diferentes às vezes produziam resultados muito diferentes. E a regularização, pelo contrário, permite obter resultados reproduzíveis muito mais fáceis.

Por que isso é assim? Heuristicamente, quando a função de custo não tem regularização, é provável que o comprimento do vetor de pesos aumente, sendo todas as outras coisas iguais. Com o tempo, isso pode levar a um vetor muito grande de pesos. E por isso, o vetor das escalas pode ficar travado, mostrando aproximadamente na mesma direção, pois as alterações devido à descida do gradiente fazem apenas pequenas alterações de direção com um grande comprimento do vetor. Acredito que, devido a esse fenômeno, é muito difícil para nosso algoritmo de treinamento estudar adequadamente o espaço de pesos e, portanto, é difícil encontrar um bom mínimo da função de custo.