Barulho no big data. Análise de entropia

Me deparei com uma tarefa chamada Enscombe Quartet ( Anscombe ) ”( versão em inglês ).

A Figura 1 mostra uma distribuição tabular de 4 funções aleatórias (extraídas da Wikipedia).


Fig. 1. Distribuição de tabela de quatro funções aleatórias

A Figura 2 mostra os parâmetros de distribuição dessas funções aleatórias


Fig. 2. Parâmetros de distribuição de quatro funções aleatórias

E seus gráficos na Figura 3.


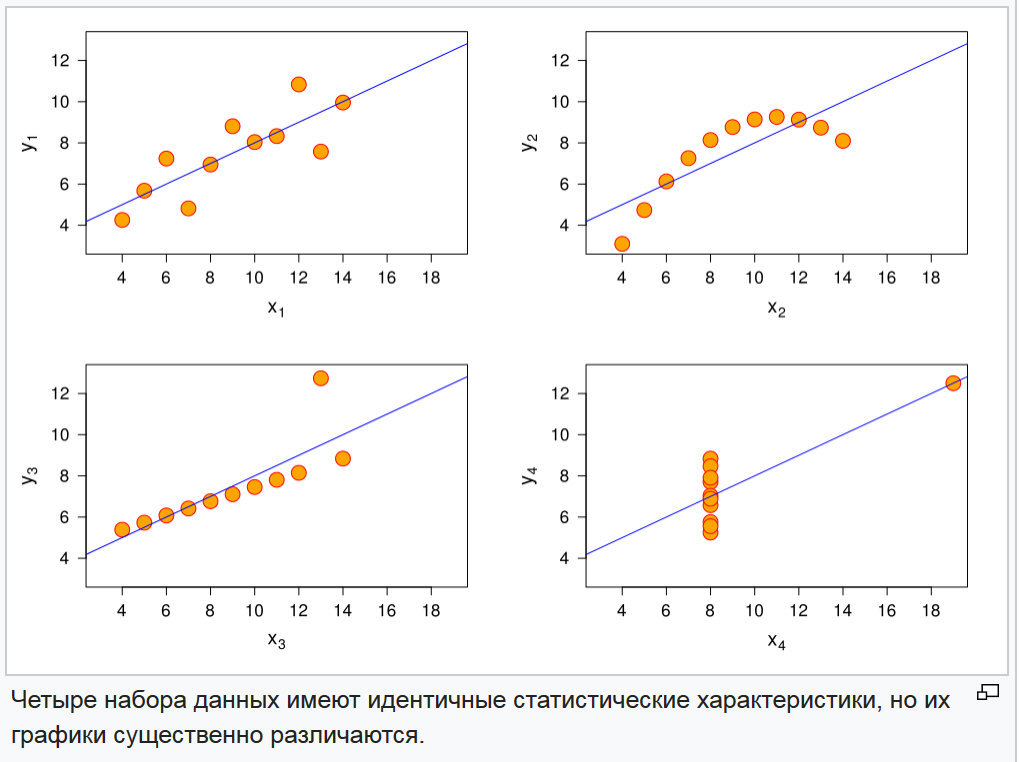Fig. 3. Gráficos de quatro funções aleatórias

O problema de distinguir essas funções é resolvido simplesmente comparando os momentos de ordens superiores e seus indicadores normalizados: coeficiente de assimetria e excesso de coeficiente. Esses indicadores são apresentados na Figura 4.


Fig. 4. Indicadores de momentos de terceira e quarta ordem e assimetria e excesso de coeficientes de quatro funções aleatórias

Como pode ser visto na tabela da Figura 4, a combinação desses indicadores para todas as funções é diferente.
A primeira conclusão, que naturalmente sugere que as informações sobre as posições relativas dos pontos são armazenadas nos parâmetros de distribuição em um nível superior à variação da distribuição aleatória.

Muitos analistas estão tentando isolar equações de regressão específicas em big data e, até o momento, atualmente, esse é um método de selecionar a equação com a menor dispersão residual. Não havia muito a acrescentar. Mas chamei a atenção para o fato de que essa é toda a informação, e a informação tem um indicador de entropia . E, entropia, tem seus limites de 0, quando a informação é completamente determinada pelo ruído branco. E o ruído branco no canal de transmissão tem uma distribuição uniforme.

Quando é necessário analisar os dados, supõe-se inicialmente que eles contenham dados relacionados que precisam ser formalizados como um relacionamento. E isso sugere que os dados não são ruído branco. Ou seja, o primeiro estágio é a seleção da equação de regressão e a determinação da variância residual. Se a regressão for escolhida corretamente, a variação residual obedecerá à lei da distribuição normal. Vamos ver e, nas Figuras 5-7, são apresentadas as fórmulas de entropia para uma variável aleatória distribuída uniformemente e normalmente distribuída.



Fig. 5. A fórmula da entropia diferencial para uma quantidade normalmente distribuída (VV Afanasyev. Teoria da probabilidade em perguntas e tarefas . Ministério da Educação e Ciência da Universidade Pedagógica da Federação Russa de Yaroslavl, em homenagem a K. D. Ushinsky)


Fig. 6. A fórmula da entropia diferencial para uma quantidade normalmente distribuída (Pugachev VS A teoria das funções aleatórias e sua aplicação a problemas de controle automático . Ed. 2º, revisado e suplementado. - M .: Fizmatlit, 1960. - 883 p.)


Fig. 7. A fórmula da entropia diferencial para uma quantidade uniformemente distribuída (Pugachev VS A teoria das funções aleatórias e sua aplicação a problemas de controle automático . Ed. 2º, revisado e suplementado. - M .: Fizmatlit, 1960. - 883 p.)

A seguir, mostramos um exemplo. Mas primeiro tomamos as condições de que cada uma das quatro funções é a coordenada do hiperplano, ou seja, ao mesmo tempo verificamos a operação do modelo no espaço multidimensional. Desenhe uma convolução de um hipercubo em um plano. O mecanismo é apresentado na Figura 8.




Fig. 8. Dados iniciais com o mecanismo de convolução


Fig. 9. Agrupamento agregado na figura.


Fig. 10. Parâmetros de distribuição de quatro funções aleatórias e um agrupamento sumário.

Considere o mecanismo para escolher o tamanho do intervalo da partição. As condições iniciais são apresentadas na Figura 11.


Fig. 11. As condições iniciais para dividir em intervalos.

Condição 1. Deve ter uma probabilidade diferente de zero na região de variação, pois, caso contrário, a entropia é igual ao infinito. Tanto para a amostra inicial quanto para o residual.

Condição 2. Como é impossível ignorar a possibilidade de discrepância em novos dados, etc., para intervalos extremos, é necessário estabelecer a probabilidade de acordo com a lei teórica normal ou outra geralmente aceita pela lei da distribuição de probabilidade, de acordo com o princípio da probabilidade de cauda.

Condição 3. A etapa do intervalo deve fornecer o número mínimo necessário de intervalos na propagação da amostra residual.

Condição 4. O número de intervalos deve ser ímpar.

Condição 5. O número de intervalos deve garantir concordância confiável com a lei teórica de distribuição selecionada para o estudo.


Fig. 12. O restante da distribuição

Defina o mecanismo de seleção de intervalos na Figura 13.


Fig. 13. O algoritmo de seleção de intervalo

O principal problema, na minha opinião, foi decidir entre introduzir intervalos de cauda ou não. Se para a dispersão residual parecia bastante natural, então para as séries principais, é bastante tenso.


Fig. 14. Os resultados do processamento de valores de dados na determinação da entropia de informações

Conclusões Onde essa ferramenta pode ser aplicada

Comparando os indicadores resultantes da tabela na Figura 14, pode-se observar que eles responderam à mudança na estrutura de dados. E isso significa que a ferramenta possui sensibilidade e permite resolver problemas semelhantes à tarefa do quarteto Enskomb.

Sem dúvida, esses problemas podem ser resolvidos com a ajuda de momentos de ordens superiores. Mas, em sua essência, a entropia informacional depende da variação de uma variável aleatória, ou seja, é uma característica de variação de terceiros. Assim, podemos indicar os intervalos em que o uso da análise de variância pode levar a um resultado específico.

A característica numérica da entropia torna possível realizar uma análise de correlação com variáveis ​​independentes. Como exemplo da manifestação de uma possível conexão, o seguinte: suponha que, durante o intervalo de a a b, o nível de ruído de uma série de dados tenha aumentado, comparando os valores de variáveis ​​independentes, descobrimos que a variável xn entrou no intervalo de mais de 5 unidades, depois variável, diminuiu abaixo de +5, ruído diminuiu. Além disso, uma verificação adicional pode ser feita e, se essa hipótese for confirmada, em outros estudos, proibir a variável xn de subir acima de +5. Como nesse caso, os dados se tornam inúteis.

Presumo que existem outras opções para usar esta ferramenta.

Como usar

Nesse aspecto, o mecanismo natural da “média móvel” é examinado, suponho que o tamanho da amostra obtido pela fórmula de tamanho da amostra da análise estatística proporcionará um volume razoável da área de escorregamento. De acordo com a análise atual, concluiu-se que o tamanho da amostra deve ser determinado a partir da proporção mínima que cai na menor probabilidade. No nosso exemplo, para a variação residual, a fração mínima do intervalo empírico é 0,15909. Isso deve ser feito, porque, se algum intervalo no volume de escorregamento estiver vazio, nesse caso, o número de ruído será ultrajante ou a regra funcionará que o logaritmo de 0 seja igual a menos o infinito. E com um tamanho de amostra selecionado corretamente, os valores transcendentais deste indicador indicarão uma mudança importante na estrutura da informação.