Vários colegas enfrentam o problema de que, para calcular algum tipo de métrica, por exemplo, taxa de conversão, é necessário validar todo o banco de dados. Ou você precisa realizar um estudo detalhado para cada cliente, onde existem milhões de clientes. Esse tipo de kerry pode funcionar por algum tempo, mesmo em repositórios feitos especialmente. Não é muito divertido esperar 5-15-40 minutos até que uma métrica simples seja considerada para descobrir que você precisa calcular outra coisa ou adicionar outra.
Uma solução para esse problema é a amostragem: não estamos tentando calcular nossa métrica em toda a matriz de dados, mas utilizamos um subconjunto que representa representativamente as métricas de que precisamos. Essa amostra pode ser 1000 vezes menor que nossa matriz de dados, mas é boa o suficiente para mostrar os números de que precisamos.
Neste artigo, decidi demonstrar como o tamanho da amostra afeta o erro métrico final.
O problema
A questão principal é: quão bem a amostra descreve a "população"? Como coletamos uma amostra de uma matriz comum, as métricas que recebemos acabam sendo variáveis aleatórias. Amostras diferentes nos fornecerão diferentes resultados métricos. Diferente, não significa nenhum. A teoria da probabilidade nos diz que os valores das métricas obtidos por amostragem devem ser agrupados em torno do valor real da métrica (realizado em toda a amostra) com um certo nível de erro. Além disso, geralmente temos problemas em que um nível de erro diferente pode ser dispensado. Uma coisa é descobrir se obtemos uma conversão de 50% ou 10% e outra é obter um resultado com uma precisão de 50,01% vs 50,02%.
É interessante que, do ponto de vista da teoria, o coeficiente de conversão observado por nós em toda a amostra também seja uma variável aleatória, porque A taxa de conversão "teórica" só pode ser calculada em uma amostra de tamanho infinito. Isso significa que mesmo todas as nossas observações no banco de dados fornecem uma estimativa de conversão com precisão, embora nos pareça que esses números calculados sejam absolutamente precisos. Também leva à conclusão de que, mesmo que hoje a taxa de conversão seja diferente de ontem, isso não significa que algo mudou, mas apenas significa que a amostra atual (todas as observações no banco de dados) é da população em geral (todas as possíveis observações para este dia, que ocorreram e não ocorreram) deram um resultado ligeiramente diferente do que ontem. De qualquer forma, para qualquer produto ou analista honesto, essa deve ser uma hipótese básica.
Digamos que temos 1.000.000 de registros em um banco de dados do tipo 0/1, que nos informa se ocorreu uma conversão em um evento. Então a taxa de conversão é simplesmente a soma de 1 dividido por 1 milhão.
Pergunta: se coletarmos uma amostra do tamanho N, qual e com qual probabilidade a taxa de conversão será diferente da calculada em toda a amostra?
Considerações teóricas
A tarefa é reduzida ao cálculo do intervalo de confiança do coeficiente de conversão para uma amostra de um determinado tamanho para uma distribuição binomial.
Da teoria, o desvio padrão para a distribuição binomial é:
S = sqrt (p * (1 - p) / N)
Onde
p - taxa de conversão
N - Tamanho da amostra
S - desvio padrão
Não considerarei o intervalo de confiança direto da teoria. Existe um matan bastante complicado e confuso, que finalmente relaciona o desvio padrão e a estimativa final do intervalo de confiança.
Vamos desenvolver uma "intuição" sobre a fórmula do desvio padrão:
- Quanto maior o tamanho da amostra, menor o erro. Nesse caso, o erro cai na dependência quadrática inversa, ou seja, aumentar a amostra em 4 vezes aumenta a precisão em apenas 2 vezes. Isso significa que, em algum momento, aumentar o tamanho da amostra não trará vantagens particulares e também significa que uma precisão bastante alta pode ser obtida com uma amostra relativamente pequena.

- Existe uma dependência do erro no valor da taxa de conversão. O erro relativo (ou seja, a razão do erro em relação ao valor da taxa de conversão) tem uma tendência "vil" de ser maior, menor a taxa de conversão:
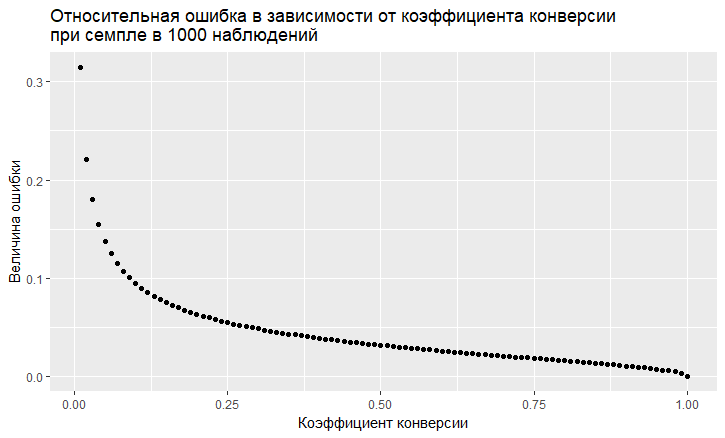
- Como vemos, o erro "voa" para o céu com uma baixa taxa de conversão. Isso significa que, se você provar eventos raros, precisará de tamanhos de amostra grandes; caso contrário, obterá uma estimativa de conversão com um erro muito grande.
Modelagem
Podemos nos afastar completamente da solução teórica e resolver o problema "de frente". Graças à linguagem R, agora é muito fácil de fazer. Para responder à pergunta, qual é o erro que recebemos ao fazer a amostragem, basta fazer mil amostras e ver qual o erro que obtemos.
A abordagem é a seguinte:
- Adotamos diferentes taxas de conversão (de 0,01% a 50%).
- Coletamos 1000 amostras de 10, 100, 1000, 10000, 50.000, 100.000, 250.000, 500.000 elementos na amostra
- Calculamos a taxa de conversão para cada grupo de amostras (1000 coeficientes)
- Construímos um histograma para cada grupo de amostras e determinamos até que ponto 60%, 80% e 90% das taxas de conversão observadas se situam.
Código R que gera dados:
sample.size <- c(10, 100, 1000, 10000, 50000, 100000, 250000, 500000) bootstrap = 1000 Error <- NULL len = 1000000 for (prob in c(0.0001, 0.001, 0.01, 0.1, 0.5)){ CRsub <- data.table(sample_size = 0, CR = 0) v1 = seq(1,len) v2 = rbinom(len, 1, prob) set = data.table(index = v1, conv = v2) print(paste('probability is: ', prob)) for (j in 1:length(sample.size)){ for(i in 1:bootstrap){ ss <- sample.size[j] subset <- set[round(runif(ss, min = 1, max = len),0),] CRsample <- sum(subset$conv)/dim(subset)[1] CRsub <- rbind(CRsub, data.table(sample_size = ss, CR = CRsample)) } print(paste('sample size is:', sample.size[j])) q <- quantile(CRsub[sample_size == ss, CR], probs = c(0.05,0.1, 0.2, 0.8, 0.9, 0.95)) Error <- rbind(Error, cbind(prob,ss,t(q))) }
Como resultado, obtemos a tabela a seguir (haverá gráficos posteriormente, mas os detalhes são mais visíveis na tabela).
Vamos ver os casos com 10% de conversão e com uma baixa conversão de 0,01%, porque todos os recursos do trabalho com amostragem são claramente visíveis neles.
Com 10% de conversão, a imagem parece bem simples:

Os pontos são as arestas do intervalo de confiança de 5 a 95%, ou seja, Ao fazer uma amostra, em 90% dos casos, obteremos RC na amostra dentro desse intervalo. Escala vertical - tamanho da amostra (escala logarítmica), valor da taxa de conversão horizontal. A barra vertical é um CR "verdadeiro".
Vemos a mesma coisa que vimos no modelo teórico: a precisão aumenta à medida que o tamanho da amostra cresce, e uma converge rapidamente, e a amostra obtém um resultado próximo de "verdadeiro". No total, para 1000 amostras, temos 8,6% - 11,7%, o que será suficiente para várias tarefas. E em 10 mil já 9,5% - 10,55%.
As coisas pioram com eventos raros e isso é consistente com a teoria:

A uma baixa taxa de conversão de 0,01%, o problema está nas estatísticas de 1 milhão de observações e nas amostras a situação é ainda pior. O erro é apenas gigantesco. Em amostras de até 10.000, a métrica é, em princípio, inválida. Por exemplo, em uma amostra de 10 observações, meu gerador recebeu 0 conversão 1000 vezes, então há apenas 1 ponto. Em 100 mil, temos uma dispersão de 0,005% a 0,0016%, ou seja, podemos fazer quase metade do coeficiente com essa amostragem.
Também é importante notar que, quando você observa uma conversão de uma escala tão pequena em 1 milhão de tentativas, simplesmente tem um grande erro natural. A partir disso, conclui-se que conclusões sobre a dinâmica de tais eventos raros devem ser feitas em amostras realmente grandes; caso contrário, você simplesmente persegue fantasmas, flutuações aleatórias nos dados.
Conclusões:
- Amostragem de um método de trabalho para obter estimativas
- A precisão da amostra aumenta com o aumento do tamanho da amostra e diminui com a diminuição da taxa de conversão.
- A precisão das estimativas pode ser modelada para sua tarefa e, assim, escolha a amostra ideal para você.
- É importante lembrar que eventos raros não provam bem
- Em geral, eventos raros são difíceis de analisar, pois exigem grandes amostras de dados sem amostras.