Algoritmo criptográfico Grasshopper: praticamente o complexo

Este artigo detalha o algoritmo de criptografia de bloco definido no GOST R 34.12-2015 como o Grasshopper. Em que se baseia, qual é a matemática dos algoritmos criptográficos de blocos e como esse algoritmo é implementado em java.

Quem, como, quando e por que desenvolveu esse algoritmo permanecerá fora do escopo do artigo, pois neste caso temos pouco interesse, exceto:

Gafanhoto = Kuznetsov, Nechaev E Companhia.



Como a criptografia é baseada principalmente em matemática, para que uma explicação adicional não cause muitas perguntas, você deve primeiro analisar os conceitos básicos e as funções matemáticas nas quais esse algoritmo é construído.

Campos Galois

A aritmética dos campos de Galois é aritmética polinomial, ou seja, cada elemento desse campo é um polinômio. O resultado de qualquer operação também é um elemento desse campo. Um campo Galois específico consiste em um intervalo fixo de números. A característica do campo é chamada de número primo p. Ordem de campo, ou seja, a quantidade de seus elementos é um certo grau natural de característica $$$p ^ m$ , onde m ϵ N. Para m = 1, o campo é chamado simples. Nos casos em que m> 1, para a formação de um campo, também é necessário um polinômio gerador de grau m; esse campo é chamado de estendido. $$$Gf (p ^ m)$ - designação do campo de Galois. O polinômio gerador é irredutível, isto é, simples (por analogia com números primos, é divisível por 1 e por si só, sem resto). Como trabalhar com qualquer informação está funcionando com bytes e um byte é de 8 bits, use como campo $$$Gf (2 ^ 8)$ e o polinômio gerador:

$$

$$x ^ 8 + x ^ 7 + x ^ 6 + x + 1.$$

No entanto, para começar, analisaremos as operações básicas em um campo mais simples $$$Gf (2 ^ 3)$ com a geração de polinômios $$$f (x) = x ^ 3 + x + 1$ .

Operação de adição

A mais simples é a operação de adição, que na aritmética de campo de Galois é uma simples adição bit a módulo 2 (R).

Chamo imediatamente a atenção para o fato de que o sinal "+" aqui e a seguir se refere à operação do XOR bit a bit, e não à adição na forma usual.

A tabela verdade da função HOR



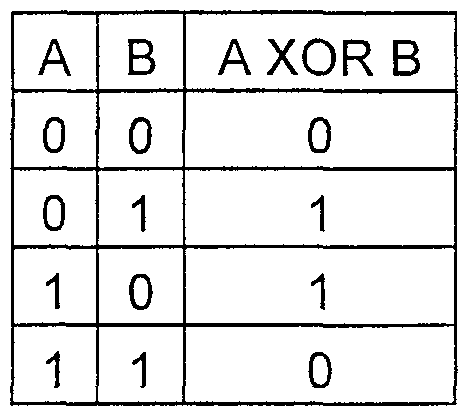
Um exemplo: $$$5 + 3 = 101 + 011 = 110_2 = 6_ {10}$

Na forma polinomial, esta operação será semelhante a

$$

$$(x ^ 2 + 1) + (x + 1) = x ^ 2 + x = 110_2 = 6_ {10}$$

Operação de multiplicação

Para realizar a operação de multiplicação, é necessário converter os números em forma polinomial:

$$

$$5 = 101_2 = 1 * x ^ 2 + 0 * x ^ 1 + 1 * x ^ 0 = x ^ 2 + 1$$

Como você pode ver, o número na forma polinomial é um polinômio cujos coeficientes são os valores dos dígitos na representação binária do número.

Multiplique dois números na forma polinomial:

$$

$$

$$= x ^ 4 + x ^ 3 + x + 1 = 11011_2 = 27_ {10}$$

O resultado da multiplicação 27 não está no campo usado. $$$Gf (2 ^ 3)$ (consiste em números de 0 a 7, como mencionado acima). Para combater esse problema, é necessário usar um polinômio gerador.

Supõe-se também que x satisfaz a equação $$$f (x) = x ^ 3 + x + 1 = 0$ então



Vamos fazer uma tabuada de multiplicação:



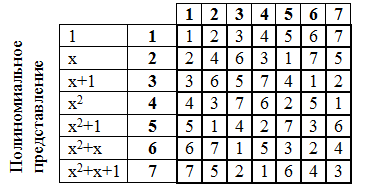
De grande importância é a tabela de graus dos elementos do campo de Galois. A elevação a uma potência também é realizada em forma polinomial, semelhante à multiplicação.

Um exemplo:

$$

$$

$$= x (x ^ 3 + x + 1) + x ^ 2 + x + 1 = x ^ 2 + x + 1 = 111_2 = 7_ {10}$$

Assim, compilamos uma tabela de graus:



A tabela de graus é cíclica: o sétimo grau corresponde a zero, então o oitavo corresponde ao primeiro, etc. Você pode verificar isso se desejar.

Nos campos de Galois, existe o conceito de um termo primitivo - um elemento de um campo cujos graus contêm todos os elementos diferentes de zero do campo. Pode-se ver que todos os elementos correspondem a essa condição (bem, exceto 1, é claro). No entanto, esse nem sempre é o caso.

Para os campos que estamos considerando, ou seja, com a característica 2, sempre escolha 2. Como membro primitivo, dada sua propriedade, qualquer elemento do campo pode ser expresso em termos do grau do membro primitivo.



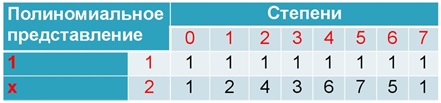
Um exemplo: $$$5 = 2 ^ 6,7 = 2 ^ 5$

Usando essa propriedade e levando em consideração a ciclicidade da tabela de graus, tentaremos multiplicar os números novamente:

$$

$$5 * 7 = 2 ^ 6 * 2 ^ 5 = 2 ^ {(6 + 5)} = 2 ^ {(11mod7)} = 2 ^ 4 = 6$$

O resultado coincidiu com o que calculamos anteriormente.

Agora vamos fazer a divisão:

$$

$$6/5 = 2 ^ 4/2 ^ 6 = 2 ^ {(4-6)} = 2 ^ {((- 2) mod7)} = 2 ^ 5 = 7$$

O resultado obtido também é verdadeiro.

Bem, por uma questão de completude, vejamos o aumento da potência:

$$

$$5 ^ 2 = (2 ^ 6) ^ 2 = 2 ^ {(6 * 2)} = 2 ^ {(12mod7)} = 2 ^ 5 = 7$$

Essa abordagem para multiplicação e divisão é muito mais simples do que operações reais usando polinômios, e para elas não há necessidade de armazenar uma grande tabela de multiplicação, mas apenas uma linha de graus de um membro de campo primitivo.

Agora de volta ao nosso campo $$$Gf (2 ^ 8)$

O elemento zero do campo é um, o 1º é um dois, cada elemento subsequente do 2º ao 254º elemento é calculado como o anterior, multiplicado por 2, e se o elemento estiver fora do campo, ou seja, seu valor será maior que $$$(2 ^ 8-1)$ então XOR é feito com o número $$$195_ {10}$ , esse número representa o polinômio irredutível do campo $$ , trazemos esse número para o campo $$$451-256 = $ 19$ . E o 255º elemento é novamente 1. Portanto, temos um campo contendo 256 elementos, ou seja, um conjunto completo de bytes, e analisamos as operações básicas que são executadas nesse campo.



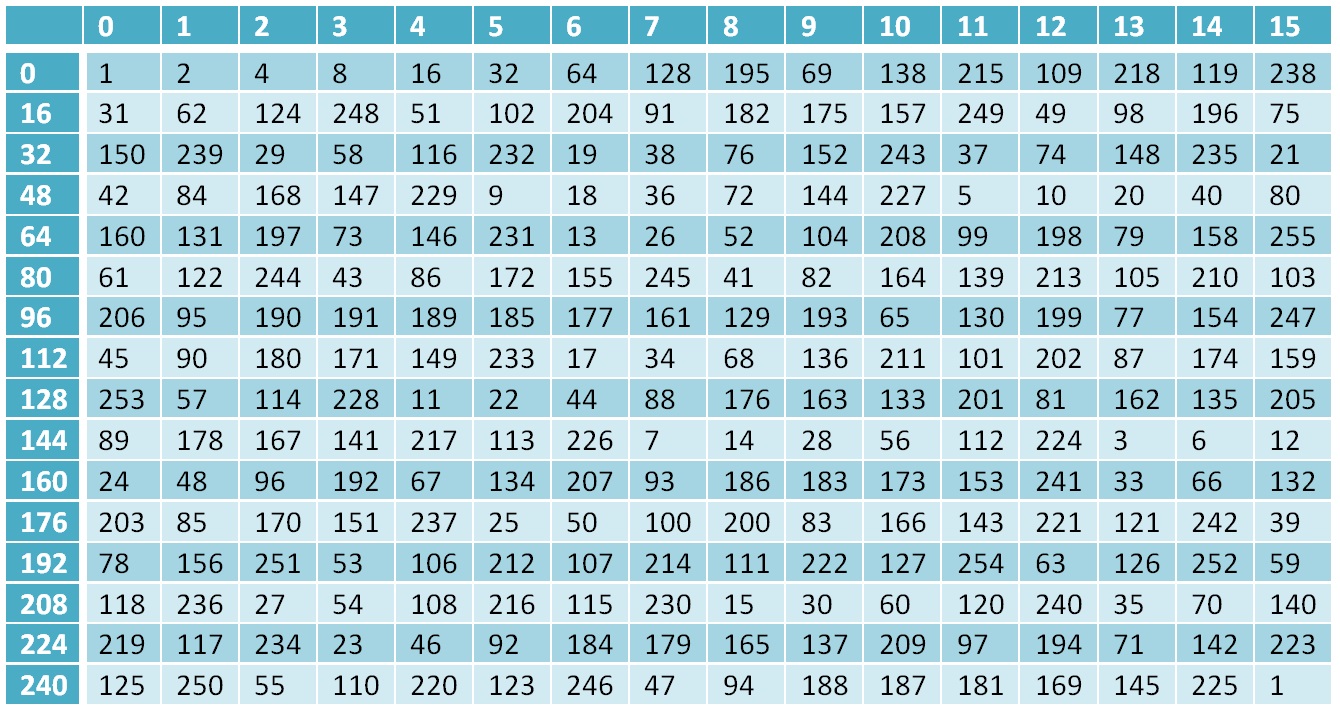
Tabela de potências de dois para o campo $$$Gf (2 ^ 8)$

Por que foi necessário - parte dos cálculos no algoritmo Grasshopper é realizada no campo Galois, e os resultados dos cálculos, respectivamente, são elementos desse campo.

Rede Feistel

A Rede Feistel é um método de criptografia em bloco desenvolvido por Horst Feistel na IBM em 1971. Hoje, a rede de Feistel é a base de um grande número de protocolos criptográficos.

A rede Feistel opera com blocos de texto não criptografado:

1. O bloco é dividido em duas partes iguais - esquerda e direita R.
2. O sub-bloco esquerdo L é alterado pela função f usando a tecla K: X = f (L, K). Como função, pode haver qualquer transformação.
3. O sub-bloco resultante X é adicionado ao módulo 2 com o sub-bloco direito R, que permanece inalterado: X = X + R.
4. As peças resultantes são trocadas e coladas.

Essa sequência de ações é chamada de célula Feistel.


Figura 1. Célula Feistel

A rede Feistel consiste em várias células. Os sub-blocos obtidos na saída da primeira célula vão para a entrada da segunda célula, os sub-blocos resultantes da segunda célula vão para a entrada da terceira célula e assim por diante.

Algoritmo de criptografia

Agora, nos familiarizamos com as operações usadas e podemos passar para o tópico principal - ou seja, o algoritmo de criptografia Grasshopper.

A base do algoritmo é a chamada rede SP - rede de permuta-substituição. A cifra baseada na rede SP recebe um bloco e uma chave na entrada e executa várias rodadas alternadas que consistem em estágios de substituição e estágios de permutação. O Grasshopper realiza nove rodadas completas, cada uma das quais inclui três operações consecutivas:

1. A operação de aplicação de uma chave redonda ou XOR bit a bit de uma chave e um bloco de dados de entrada;
2. Conversão não linear, que é uma simples substituição de um byte por outro, de acordo com a tabela;
3. Transformação linear. Cada byte do bloco é multiplicado no campo Galois por um dos coeficientes da série (148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148, 1), dependendo do ordinal números de bytes (uma série é apresentada para números de série de 15 a 0, conforme mostrado na figura). Os bytes são adicionados juntos ao módulo 2, e todos os 16 bytes do bloco são deslocados para a ordem baixa, e o número resultante é gravado no lugar do byte lido.

A última décima rodada não está concluída, inclui apenas a primeira operação XOR.

O Grasshopper é um algoritmo de bloco, funciona com blocos de dados de 128 bits ou 16 bytes de comprimento. O comprimento da chave é de 256 bits (32 bytes).


Figura 2. O esquema de criptografia e descriptografia do bloco de dados

O diagrama mostra a sequência de operações, onde S é uma transformação não linear, L é uma transformação linear, Ki são teclas redondas. A questão surge imediatamente - de onde vêm as teclas redondas.

Formação de Teclas Redondas

Chaves iterativas (ou redondas) são obtidas por certas transformações baseadas em uma chave mestra, cujo comprimento, como já sabemos, é de 256 bits. Esse processo começa dividindo a chave mestra ao meio, para que o primeiro par de chaves redondas seja obtido. Oito iterações da rede Feistel são usadas para gerar cada par subsequente de chaves redondas, uma constante é usada em cada iteração, que é calculada aplicando uma transformação linear do algoritmo no valor do número da iteração.


O esquema para obter chaves iterativas (redondas)

Se lembrarmos da Figura 1, o sub-bloco esquerdo L é a metade esquerda da chave original, o sub-bloco direito R é a metade direita da chave original, K é a constante Ci, a função f é a sequência de operações R XOR Ci, transformação não linear, transformação linear.

As constantes de iteração Ci são obtidas usando a transformação L do número de sequência da iteração.

Portanto, para criptografar um bloco de texto, primeiro precisamos calcular 32 constantes iterativas, depois calcular 10 chaves redondas com base na chave e executar a sequência de operações mostrada na Figura 2.

Vamos começar calculando as constantes:
Primeira const $$$C_1 = 1_ {10} = 00000001_2 = 01_ {16}$ No entanto, todas as transformações em nosso algoritmo são realizadas com blocos de 16 bytes, portanto é necessário suplementar a constante com o comprimento do bloco, ou seja, adicionar 15 bytes zero à direita, obtemos

$$

$$C_1 = 010000000000000000000000000000000000$$

Multiplique-o por uma série (1, 148, 32, 133, 16, 194, 192, 1, 251, 1, 192, 194, 16, 133, 32, 148) da seguinte maneira:

$$

$$a_ {15} = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 +$$

$$

$$+ a_5 * 194 + a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

(essa igualdade é dada nas operações dos campos de Galois)
Como tudo, exceto o byte zero, é igual a 0 e o byte zero é multiplicado por 1, obtemos 1 e o escrevemos na ordem mais alta do número, deslocando todos os bytes para a ordem mais baixa, obtemos:

$$

$$C_1 = 0000000000000000000000000000000000$$

Repita as mesmas operações. Desta vez $$$a_ {15} = 1$ , todos os outros bytes são 0, portanto, apenas o primeiro permanece nos termos $$$a_ {15} * 148 = 1 * 148 = 148_ {10} = 94_ {16}$ nós obtemos:

$$

$$C_1 = 00000000000000000000000000000000194$$

Fazemos a terceira iteração, eis dois termos diferentes de zero:

$$

$$a_ {15} * 148 + a_ {14} * 32 = 148 * 148 + 1 * 32 =$$

$$

$$100100100 * 10010100 + 00000001 * 00100000 =$$

$$

$$= (x ^ 7 + x ^ 4 + x ^ 2) * (x ^ 7 + x ^ 4 + x ^ 2) + 1 * x ^ 5 = x ^ {14} + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 6 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {13} + x ^ {12} + x ^ 7 + x ^ 6 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 5 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {11} + x ^ 5 + x ^ 7 + x ^ 8 + x ^ 4 + x ^ 5 =$$

$$

$$= x ^ 3 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ {10} + x ^ 9 + x ^ 3 + x ^ 8 + x ^ 7 =$$

$$

$$= x ^ 2 (x ^ 8 + x ^ 7 + x ^ 6 + x + 1) + x ^ 2 + x ^ 7 = x ^ 7 + x ^ 2 = 132_ {10}$$

$$

$$132_ {10} = 84_ {16}$$

De acordo com a tabela de graus, isso poderia ser resolvido com muito mais facilidade:

$$

$$148 * 148 + 1 * 32 = 2 ^ {45} * 2 ^ {45} + 2 ^ 5 = 2 ^ {90} + 2 ^ 5 = 164 + 32 = 132$$

$$

$$C_1 = 00000000000000000000000000019484$$

Além disso, tudo é exatamente o mesmo, apenas 16 iterações para cada constante

$$

$$C_1 = 000000000000000000000000019484DD$$

$$

$$C_1 = 0000000000000000000000019484DD10$$

$$

$$C_1 = 00000000000000000000019484DD10BD$$

$$

$$C_1 = 000000000000000000019484DD10BD27$$

$$

$$C_1 = 0000000000000000019484DD10BD275D$$

$$

$$C_1 = 00000000000000019484DD10BD275DB8$$

$$

$$C_1 = 000000000000019484DD10BD275DB87A$$

$$

$$C_1 = 0000000000019484DD10BD275DB87A48$$

$$

$$C_1 = 00000000019484DD10BD275DB87A486C$$

$$

$$C_1 = 000000019484DD10BD275DB87A486C72$$

$$

$$C_1 = 0000019484DD10BD275DB87A486C727$$

$$

$$C_1 = 00019484DD10BD275DB87A486C7276A2$$

E a constante final:

$$

$$C_1 = 019484DD10BD275DB87A486C7276A2E6$$

Outras constantes:

$$

$$C_2 = 02EBCB7920B94EBAB3F490D8E4EC87DC$$

$$

$$C_3 = 037F4FA4300469E70B8ED8B4969A25B2$$

$$

$$C_4 = 041555F240B19CB7A52BE3730B1BCD7B$$

$$

$$C_5 = 0581D12F500CBBEA1D51AB1F796D6F15$$

$$

$$C_6 = 06FE9E8B6008D20D16DF73ABEFF74AA7$$

$$

$$C_7 = 076A1A5670B5F550AEA53BC79D81E8C9$$

$$

$$C_8 = 082AAA2780A1FBAD895605E6163659F6$$

$$

$$C_9 = 09BE2EFA901CDCF0312C4D8A6440FB98$$

$$

$$C_ {10} = 0AC1615EA018B5173AA2953EF2DADE2A$$

$$

$$C_ {11} = 0B55E583B0A5924A82D8DD5280AC7C44$$

$$

$$C_ {12} = 0C3FFFD5C010671A2C7DE6951D2D948D$$

$$

$$C_ {13} = 0DAB7B08D0AD40479407AEF96F5B36E3$$

$$

$$C_ {14} = 0ED434ACE0A929A09F89764DF9C11351$$

$$

$$C_ {15} = 0F40B071F0140EFD27F33E218BB7B13F$$

$$

$$C_ {16} = 1054974EC3813599D1AC0A0F2C6CB22F$$

$$

$$C_ {17} = 11C01393D33C12C469D642635E1A1041$$

$$

$$C_ {18} = 12BF5C37E3387B2362589AD7C88035F3$$

$$

$$C_ {19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$$

$$

$$C_ {20} = 1441C2BC8330A92E7487E97C27777F54$$

$$

$$C_ {21} = 15D54661938D8E73CCFDA1105501DD3A$$

$$

$$C_ {22} = 16AA09C5A389E794C77379A4C39BF888$$

$$

$$C_ {23} = 173E8D18B334C0C97F0931C8B1ED5AE6$$

$$

$$C_ {24} = 187E3D694320CE3458FA0FE93A5AEBD9$$

$$

$$C_ {25} = 19EAB9B4539DE969E0804785482C49B7$$

$$

$$C_ {26} = 1A95F6106399808EEB0E9F31DEB66C05$$

$$

$$C_ {27} = 1B0172CD7324A7D35374D75DACC0CE6B$$

$$

$$C_ {28} = 1C6B689B03915283FDD1EC9A314126A2$$

$$

$$C_ {29} = 1DFFEC46132C75DE45ABA4F6433784CC$$

$$

$$C_ {30} = 1E80A3E223281C394E257C42D5ADA17E$$

$$

$$C_ {31} = 1F14273F33953B64F65F342EA7DB0310$$

$$

$$C_ {32} = 20A8ED9C45C16AF1619B141E58D8A75E$$

Agora vamos calcular as chaves redondas de acordo com o esquema apresentado acima, pegue a chave de criptografia:

$$

$$K = 7766554433221100FFEEDDCCBBAA9988$$

$$

Então

$$

$$K_1 = 7766554433221100FFEEDDCCBBAA9988$$

$$

$$K_2 = EFCDAB89674523011032547698BADCFE$$

$$$K_1$ será o sub-bloco esquerdo da rede Feistel e $$$K_2$ - certo.
Vamos fazer a operação $$$K_1 + C_1$
Primeiro byte $$$K_1$ é igual a $$$77_ {16} = 01110111_2$
Primeiro byte $$$C_1$ é igual a $$$01_ {16} = 00000001_2$

$$

$$01110111_2 + 00000001_2 = 01110110_2 = 76_ {16}$$

os bytes restantes são convertidos da mesma maneira, como resultado $$$X (K_1, C_1) = K_1 + C_1$ :

$$

$$X (K_1, C_1) = 76F2D199239F365D479495A0C9DC3BE6$$

Em seguida, realizamos uma transformação não linear $$$S (X (K_1, C_1))$ . É realizado de acordo com a tabela:


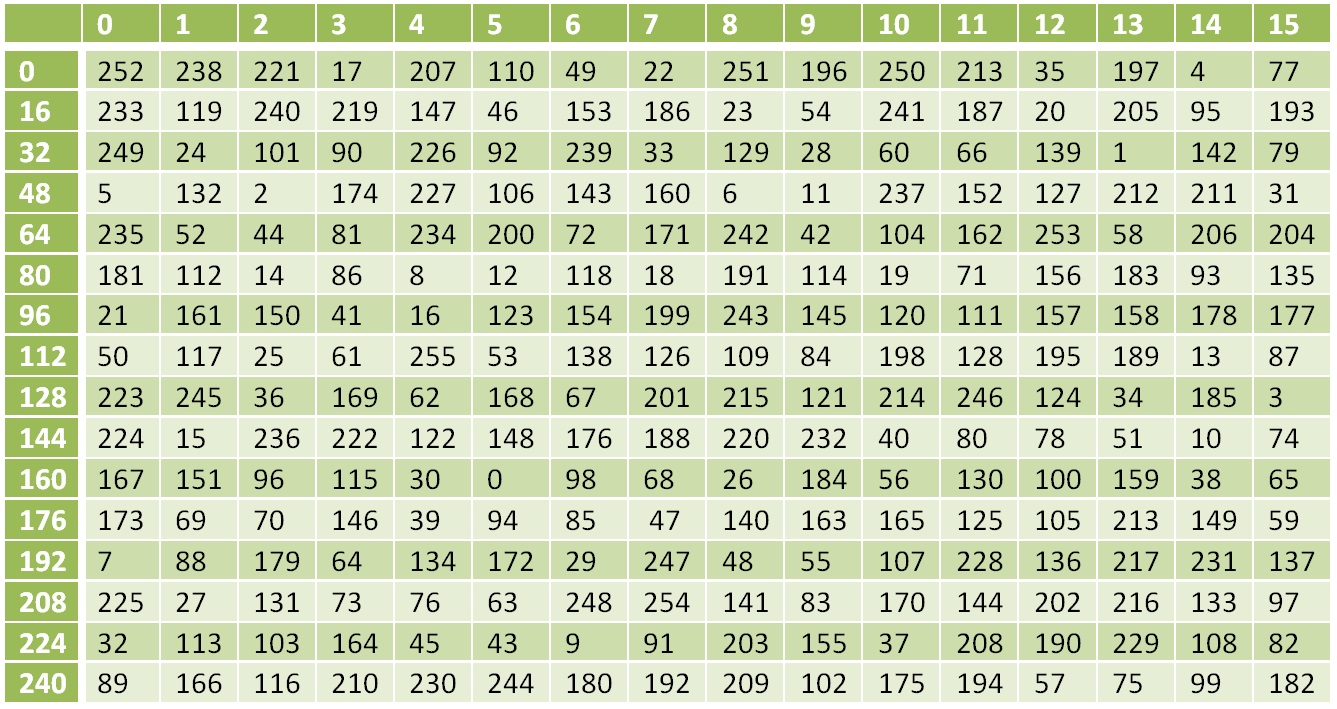Tabela de conversão não linear

O número 0 é substituído por 252, 1 por 238, 17 por 119, etc.

$$

$$76_ {16} = 118_ {10}$$

$$

$$S (118) = 138_ {10} = 8A_ {16}$$

$$

$$S (X (K_1, C_1)) = 8A741BE85A4A8FB7AB7A94A737CA9809$$

Agora execute uma transformação linear $$$L (S (X (K_1, C_1)))$ , foi considerado em detalhes ao calcular constantes iterativas; portanto, fornecemos apenas o resultado final:

$$

$$L (S (X (K_1, C_1))) = A644615E1D0757926A5DB79D9940093D$$

De acordo com o esquema da célula Feistel, realizamos XOR com o sub-bloco direito, ou seja, com $$$K_2$ :

$$

$$X (L (S (X (K_1, C_1))), K_2) = 4989CAD77A4274937A6FE3EB01FAD5C3$$

E o resultado obtido na saída da primeira célula Feistel:

$$

$$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$$

Esse valor é dividido pela metade e vai para a entrada da segunda célula Feistel, onde a segunda constante já é usada $$$C_2$ . Depois de passar por oito células, obtemos as 2 chaves a seguir $$$K_3$ e $$$K_4$ . Executaremos oito iterações da rede Feistel com eles, obteremos o próximo par de chaves e assim por diante. Oito iterações por par de chaves, já que inicialmente temos o primeiro par, então 32 iterações são realizadas no total, cada uma com sua própria constante.

Chaves restantes:

$$

$$K_3 = 448CC78CEF6A8D2243436915534831DB$$

$$

$$K_4 = 04FD9F0AC4ADEB1568ECCFE9D853453D$$

$$

$$K_5 = ACF129F44692E5D3285E4AC468646457$$

$$

$$K_6 = 1B58DA3428E832B532645C16359407BD$$

$$

$$K_7 = B198005A26275770DE45877E7540E651$$

$$

$$K_8 = 84F98622A2912AD73EDD9F7B0125795A$$

$$

$$K_9 = 17E5B6CD732FF3A52331C77853E244BB$$

$$

$$K_ {10} = 43404A8EA8BA5D755BF4BC1674DDE972$$

Bloquear criptografia

Calculamos todas as chaves e agora finalmente podemos ir diretamente para a criptografia do bloco de texto e, se você ler cuidadosamente tudo o que foi escrito acima, a criptografia do texto não será difícil, pois todas as operações usadas neste processo e sua sequência foram examinadas em detalhes.

Pegue o bloco de texto simples:

$$

$$T = 8899AABBCCDDEEFF0077665544332211$$

executar a sequência de operações X, S, L

$$

$$X (T, K_1) = FFFFFFFFFFFFFFFFFFFF99BB99FF99BB99$$

$$

$$S (X (T, K_1)) = B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8$$

$$

$$L (S (X (T, K_1))) = 30081449922F4ACFA1B055E386B697E2$$

$$

$$T_1 = 30081449922F4ACFA1B055E386B697E2$$

$$

$$X (T_1, K_2) = DFC5BFC0F56A69CEB18201951E0C4B1C$$

$$

$$S (X (T_1, K_2)) = 61AC3B07F47891E74524EE945F23A214$$

$$

$$L (S (X (T_1, K_2))) = 7290C6A158426FB396D562087A495E28$$

$$

$$T_2 = 7290C6A158426FB396D562087A495E28$$

e assim por diante, o resultado final ficará assim:

$$

$$T_ {10} = CDEDD4B9428D465A3024BCBE909D677F$$

Descriptografia de bloco

Para descriptografar o texto, você precisa usar as operações inversas na ordem inversa (veja a Fig. 2).

A operação XOR é inversa a si mesma, a inversa à operação S é a substituição de acordo com a tabela a seguir:


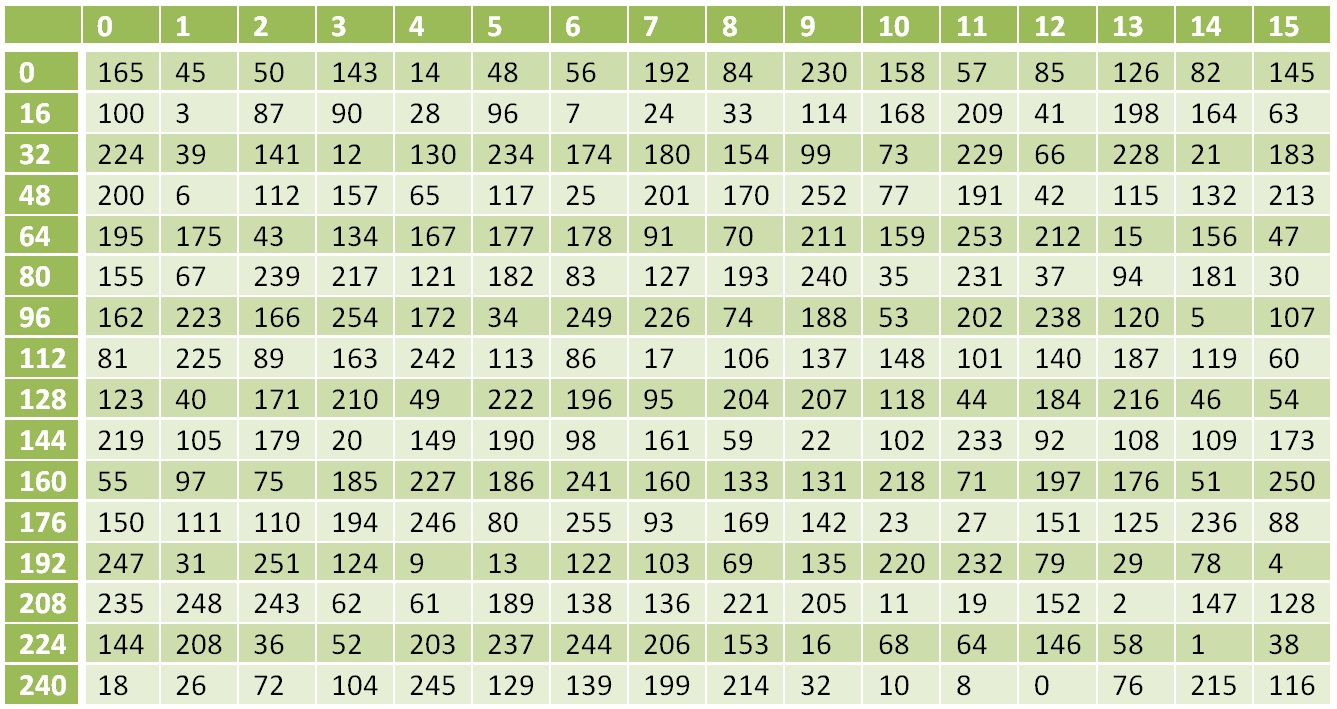Tabela de Transformação Não Linear Inversa

A transformação inversa para a função L será:

$$

$$a_0 = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$$

$$

$$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 + a_5 * 194 +$$

$$

$$+ a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$$

e uma mudança na direção do nível sênior. (Repita a operação 16 vezes)

Implementação Java

Primeiro, definimos as constantes necessárias

static final int BLOCK_SIZE = 16; //   //     static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; //     static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; //    static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; //     static byte[][] iter_C = new byte[32][16]; //     static byte[][] iter_key = new byte[10][64]; 

Vamos criar todas as principais funções:

 //  X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } //  S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; } 

Para implementar a função L, precisamos de várias funções auxiliares, uma para calcular a multiplicação de números no campo de Galois e outra para a mudança.

 //     static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } //  R     ,    L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; } 

Funções inversas:

 //  S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } //    static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // ,     static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } //     public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } //    public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } //   public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; } 

Bem, e a principal função

 static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); } 

Aprendemos a criptografar um bloco de dados para criptografar texto cujo tamanho é maior que o comprimento do bloco; existem vários modos descritos no padrão - GOST 34.13-2015:

• modo de substituição simples (livro de códigos eletrônico, BCE);
• modo gama (contador, CTR);
• modo gama com realimentação de saída (realimentação de saída, OFB);
• modo de engrenagem de substituição simples (Cipher Block Chaining, CBC);
• modo gama com feedback em texto cifrado (Cipher Feedback, CFB);
• Código de autenticação de mensagem (MAC).

Em todos os modos, o comprimento do texto deve sempre ser múltiplo do comprimento do bloco, para que o texto seja sempre preenchido à direita com um único bit e zeros ao comprimento do bloco.

O modo mais fácil é o modo de substituição simples. Nesse modo, o texto é dividido em blocos, então cada bloco é criptografado separadamente do restante, os blocos do texto cifrado são colados e recebemos uma mensagem criptografada. Esse modo é o mais simples e o mais vulnerável e quase nunca é aplicado na prática.

Outros modos podem ser considerados em detalhes posteriormente.