Estrutura de dados em árvore B

Olá pessoal! Lançamos um novo conjunto para o curso "Algoritmos para desenvolvedores" e hoje queremos compartilhar uma tradução interessante preparada para os alunos deste curso.



Nas árvores de pesquisa, como árvore de pesquisa binária, árvore AVL, árvore vermelho-preta etc. cada nó contém apenas um valor (chave) e um máximo de dois descendentes. No entanto, existe um tipo especial de árvore de pesquisa chamado B-tree (árvore bi-pronunciada). Nele, o nó contém mais de um valor (chave) e mais de dois descendentes. A árvore B foi desenvolvida em 1972 por Bayer e McCrate e foi chamada de Árvore de Pesquisa em Altura com Balanço em Altura . Seu nome moderno B-tree recebeu mais tarde.

Uma árvore B pode ser definida da seguinte forma:
Uma árvore B é uma árvore de pesquisa balanceada na qual cada nó contém muitas chaves e tem mais de dois filhos.

Aqui, o número de chaves no nó e o número de seus descendentes depende da ordem da árvore B. Cada árvore B tem um pedido.

Uma árvore B da ordem m tem as seguintes propriedades:

Propriedade 1: a profundidade de todas as folhas é a mesma.
Propriedade 2: Todos os nós, exceto a raiz, devem ter pelo menos (m / 2) - 1 chaves e no máximo m-1 .
Propriedade 3: todos os nós sem folhas, exceto a raiz (ou seja, todos os nós internos), devem ter no mínimo m / 2 descendentes.
Propriedade 4: se a raiz for um nó sem folhas, ela deve ter pelo menos 2 descendentes.
Propriedade 5: um nó sem folhas com n-1 chaves deve ter n filhos.
Propriedade 6: todas as chaves no nó devem ser organizadas em ordem crescente de seus valores.

Por exemplo, uma árvore B de 4 ordens contém no máximo 3 valores-chave e no máximo 4 filhos para cada nó.


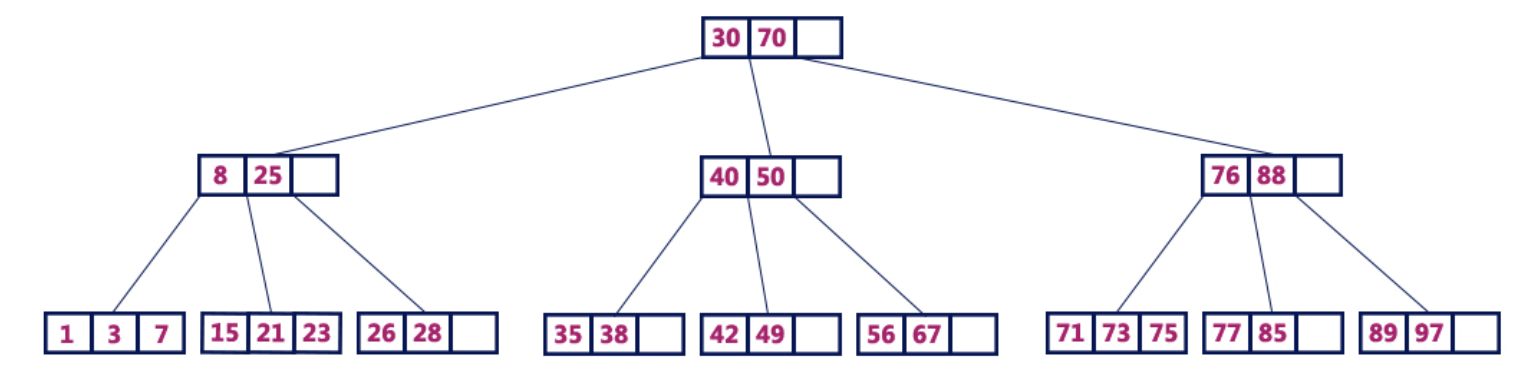Árvore B 4 pedidos

Operações em árvore B

As seguintes operações podem ser executadas na árvore B:

1. Pesquisar
2. Inserir
3. Excluir

Pesquisar B-tree

As pesquisas em árvore B são semelhantes às pesquisas em árvore binária. Na árvore de pesquisa binária, a pesquisa inicia a partir da raiz e cada vez que uma decisão bidirecional é tomada (vá ao longo da subárvore esquerda ou direita). Na árvore B, a pesquisa também começa no nó raiz, mas a cada passo é tomada uma decisão em frente e verso, onde n é o número total de descendentes do nó em questão. Na árvore B, a complexidade da pesquisa é O (log n) . A pesquisa é a seguinte:

Etapa 1: leia o item a ser pesquisado.
Etapa 2: compare o item pesquisado com o primeiro valor da chave no nó raiz da árvore.
Etapa 3: se corresponderem, imprima: "O nó encontrado!" e complete a pesquisa.
Etapa 4: se eles não corresponderem, verifique se o valor do item é mais ou menos que o valor da chave atual.
Etapa 5: se o item que você procura for menor, continue pesquisando a subárvore esquerda.
Etapa 6: se o item desejado for maior, compare o item com o próximo valor da chave no nó e repita as etapas 3, 4, 5 e 6 até encontrar uma correspondência ou até que o item pesquisado seja comparado com o último valor da chave no nó folha.
Etapa 7: se o último valor da chave no nó da lista não corresponder à pesquisa, imprima "Item não encontrado!" e complete a pesquisa.

Operação de inserção em árvore B

Na árvore B, um novo item pode ser adicionado apenas a um nó folha. Isso significa que um novo par de valores-chave é sempre adicionado apenas ao nó folha. A inserção é a seguinte:

Etapa 1: verifique se a árvore está vazia.
Etapa 2: se a árvore estiver vazia, crie um novo nó com um novo valor de chave e use-o como nó raiz.
Etapa 3: se a árvore não estiver vazia, localize um nó folha adequado ao qual um novo valor será adicionado usando a lógica da árvore de pesquisa binária.
Etapa 4: se houver uma célula vazia no nó folha atual, adicione um novo valor-chave ao nó folha atual, seguindo a ordem crescente dos valores-chave dentro do nó.
Etapa 5: se o nó atual estiver cheio e não tiver células livres, divida o nó folha enviando o valor médio ao nó pai. Repita a etapa até que o valor a ser enviado seja confirmado no nó.
Etapa 6: se a separação ocorrer com a raiz da árvore, a média se tornará a nova raiz da árvore e a altura da árvore aumentará em um.

Um exemplo:

Vamos criar uma árvore B de ordem 3 adicionando números de 1 a 10 nela.

Inserir (1):
Como "1" é o primeiro elemento da árvore, ele é inserido em um novo nó e esse nó se torna a raiz da árvore.



Inserir (2):
O elemento 2 é adicionado a um nó folha existente. Agora, temos apenas um nó, portanto, é a raiz e a folha ao mesmo tempo. Esta planilha possui uma célula vazia. Então "2" entra nesta célula vazia.



Inserir (3):
O elemento 3 é adicionado a um nó folha existente. Agora, temos apenas um nó, que é a raiz e a folha. Esta planilha não possui uma célula vazia. Portanto, separamos esse nó enviando o valor médio (2) para o nó pai. No entanto, o nó atual não possui um nó pai. Portanto, o valor médio se torna o nó raiz da árvore.



Inserir (4):
O elemento "4" é maior que o nó raiz com o valor "2", enquanto o nó raiz não é uma folha. Portanto, movemos a subárvore direita de "2". Chegamos ao nó da folha com o valor "3", que tem uma célula vazia. Assim, podemos inserir o elemento "4" nesta célula vazia.



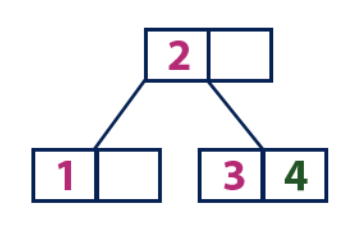Inserir (5):
O elemento "5" é maior que o nó raiz com o valor "2", enquanto o nó raiz não é uma folha. Portanto, movemos a subárvore direita de "2". Chegamos ao nó da folha e descobrimos que ele já está cheio e não possui células vazias. Em seguida, dividimos esse nó enviando o valor médio (4) para o nó pai (2). Como o nó pai possui uma célula vazia, o valor "4" é adicionado ao nó no qual já existe o valor "2" e um novo elemento "5" é adicionado como uma nova planilha.



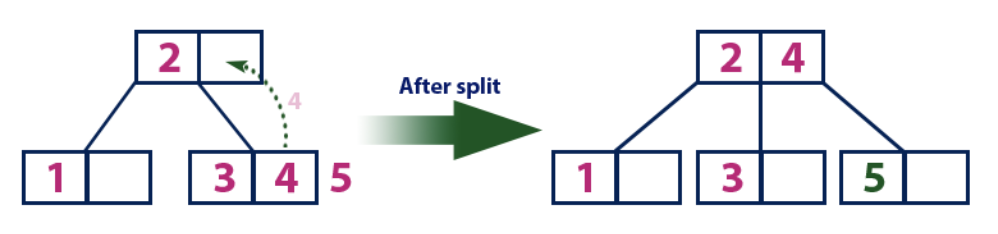Inserir (6):
O elemento "6" é maior que os elementos da raiz "2" e "4", que não são uma folha. Nós movemos ao longo da subárvore direita do elemento "4". Chegamos a uma planilha com o valor "5", que tem uma célula vazia, então o elemento "6" é colocado exatamente nela.



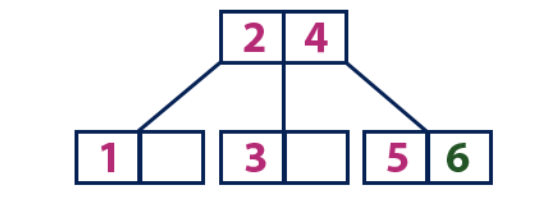Inserir (7):
O elemento "7" é maior que os elementos da raiz "2" e "4", que não são uma folha. Nós movemos ao longo da subárvore direita do elemento "4". Chegamos ao nó da folha e vemos que está cheio. Dividimos esse nó enviando o valor médio de "6" para o nó pai com os elementos "2" e "4". No entanto, o nó pai também está cheio, portanto, dividimos o nó com os elementos "2" e "4", enviando o valor "4" ao nó pai. Apenas este nó ainda não está lá. Nesse caso, o nó com o elemento "4" se torna a nova raiz da árvore.



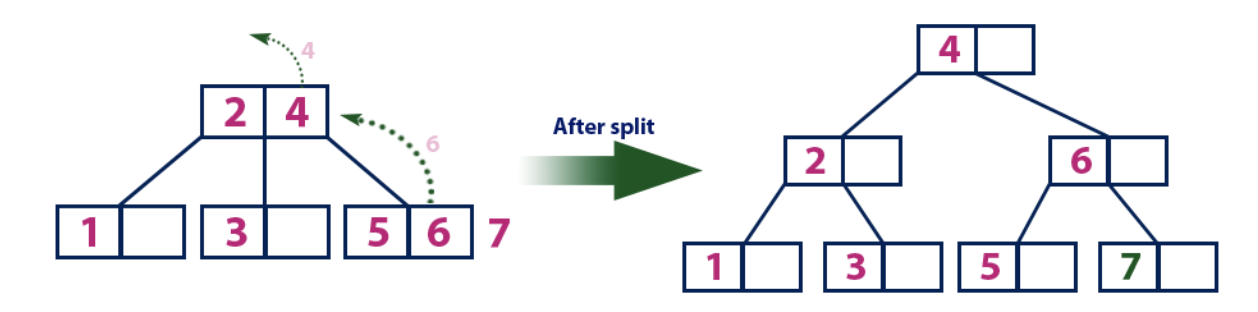Inserção (8):
O elemento 8 é maior que o nó raiz com um valor de 4 e o nó raiz não é uma folha. Movemos ao longo da subárvore direita a partir do elemento “4” e chegamos ao nó com o valor “6”. "8" é maior que "6" e o nó com o elemento "6" não é uma planilha, portanto, movemos ao longo da subárvore direita de "6". Alcançamos o nó da folha com "7", que tem uma célula vazia, então colocamos "8" nele.



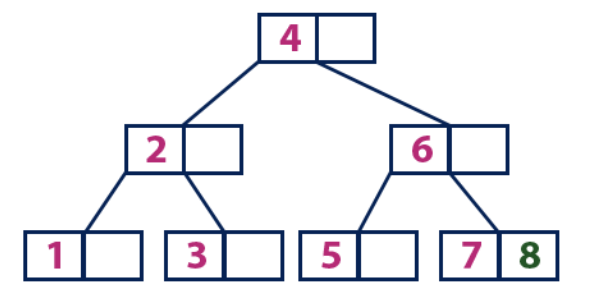Inserir (9):
O elemento 9 é maior que o nó raiz com um valor de 4 e o nó raiz não é uma folha. Movemos ao longo da subárvore direita a partir do elemento “4” e chegamos ao nó com o valor “6”. "9" é maior que "6" e o nó com o elemento "6" não é uma planilha, portanto, movemos ao longo da subárvore direita de "6". Atingimos o nó da folha com os valores "7" e "8". Ele está cheio. Dividimos esse nó enviando o valor médio (8) para o nó pai. O nó pai "6" tem uma célula vazia, então colocamos "8" nele. Nesse caso, um novo elemento "9" é adicionado à lista de nós.



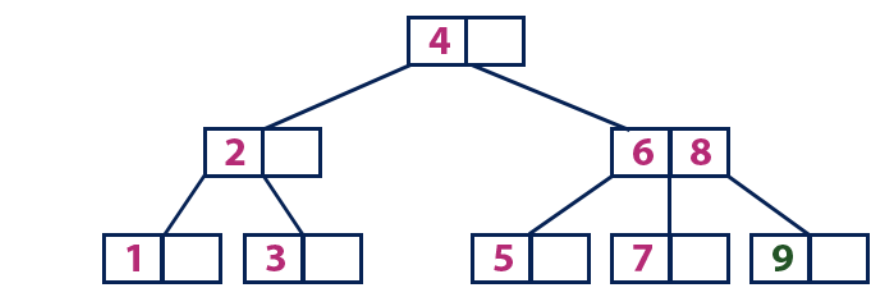
Inserir (10):
O elemento "10" é maior que o nó raiz com o valor "4", enquanto o nó raiz não é uma folha. Passamos pela subárvore direita a partir do elemento “4” e chegamos ao nó com os valores “6” e “8”. “10” é maior que “6” e “8” e o nó com esses elementos não é uma planilha; portanto, movemos-se ao longo da subárvore direita de “8”. Atingimos o nó da folha com o valor "9". Ele tem uma célula vazia, então colocamos "10" lá.



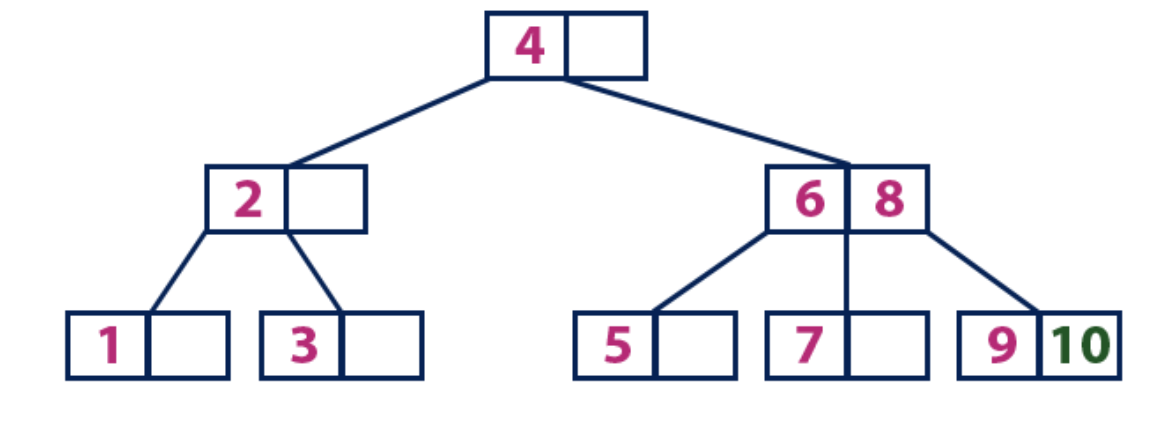
Sugerimos que você compreenda na prática como as árvores B são organizadas usando essa visualização .

Estamos esperando por todos em uma aula aberta gratuita , que será realizada no dia 12 de julho. Até breve!