De uma função matemática mágica - uma solução para governar todos eles

Três anos atrás, Marina Vyazovskaya, do Instituto Federal Suíço de Tecnologia de Lausanne, surpreendeu os matemáticos ao descobrir a maneira mais densa de empacotar esferas do mesmo tamanho em espaços de oito e 24 dimensões (no segundo caso, com a ajuda de quatro co-autores). E agora eles e co-autores provaram algo ainda mais surpreendente: configurações que resolvem o problema de empacotar esferas densamente nas dimensões mencionadas também resolvem um número infinito de outros problemas relacionados ao melhor arranjo de pontos tentando evitar um ao outro.

Os pontos, por exemplo, podem denotar um conjunto infinito de elétrons que se repelem e tentam se estabelecer na configuração com a menor energia. Ou, esses pontos podem indicar os centros de polímeros longos e retorcidos em solução, tentando se organizar para não colidir com os vizinhos. Existem muitas opções para esses problemas, e não é óbvio que cada um terá a mesma solução. Os matemáticos acreditam que, na maioria das dimensões, é muito improvável que seja esse o caso.

Mas os espaços, constituídos por 8 e 24 dimensões, contêm uma configuração especial e muito simétrica de pontos, que, como sabemos agora, solucionam simultaneamente todos esses diferentes problemas. Na linguagem da matemática, essas duas configurações são chamadas "universalmente ótimas".

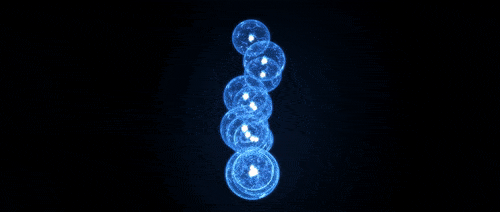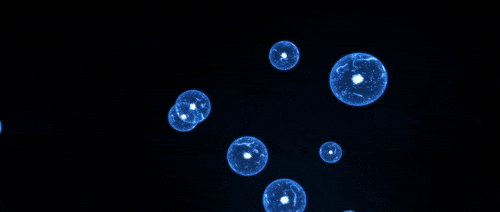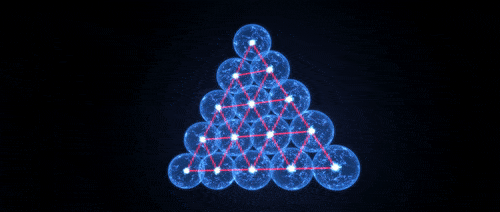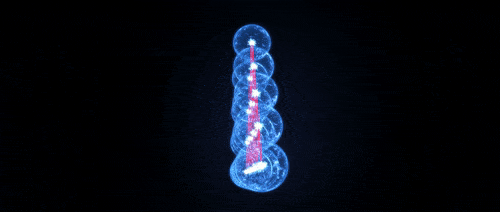
Essa nova descoberta em larga escala resume seriamente o trabalho anterior de Vyazovskaya e seus colegas. "Os fogos de artifício não pararam", disse Thomas Hales , matemático da Universidade de Pittsburgh, que provou em 1998 que o conhecido arranjo piramidal de laranjas é a maneira mais densa de empacotar esferas no espaço tridimensional.

Oito e 24 se juntam a uma dimensão em uma pequena lista de dimensões que contêm configurações universalmente ideais. No plano bidimensional, há um candidato à otimização universal - uma grade de triângulos equilaterais - mas não há provas. No mundo tridimensional, reina um zoológico completo: configurações diferentes de pontos mostram resultados diferentes em circunstâncias diferentes e, para alguns problemas, os matemáticos nem sequer têm suposições toleráveis ​​sobre a melhor configuração.

"Mude a medida ou mude a tarefa um pouco, e a situação se torna incompreensível", disse Richard Schwartz , matemático da Brown University em Providence. "Não sei por que o universo matemático é tão organizado."

Provar a otimização universal é muito mais difícil do que resolver o problema de empacotar esferas. Em particular, porque a otimização universal inclui um número infinito de tarefas diferentes ao mesmo tempo, mas também porque essas tarefas são mais complicadas em si mesmas. No empacotamento de esferas, cada esfera se preocupa apenas com seus vizinhos mais próximos, mas em um problema como a distribuição de elétrons, cada um dos elétrons interage com todos os outros, independentemente da distância entre eles. "Mesmo à luz dos meus primeiros trabalhos, eu não esperava que essa prova universalmente ótima pudesse ser feita", disse Hales.

"É muito, muito impressionante", disse Sylvia Serfati , matemática da Universidade de Nova York. "Isso está em pé de igualdade com os principais avanços matemáticos do século XIX".

Certificado mágico

Pode parecer estranho que as dimensões 8 e 24 devam se comportar de maneira diferente das, digamos, dimensões 7, 18 ou 25. Mas os matemáticos sabem há muito que a densa embalagem de objetos no espaço funciona de maneira diferente em diferentes dimensões. Por exemplo, considere uma esfera multidimensional, definida simplesmente como um conjunto de pontos localizados a uma distância fixa do centro. Se compararmos o volume da esfera com o volume do menor cubo que a descreve, quanto maior a dimensão, menor o cubo ocupa a esfera. Se você quisesse enviar uma bola de futebol de oito dimensões na menor caixa possível, a bola ocuparia menos de 2% da caixa - e todo o resto seria um espaço vazio perdido.

Em cada dimensão maior que três, é possível criar uma configuração semelhante à pirâmide de laranjas e, com dimensões crescentes, os espaços entre as esferas aumentam. Tendo atingido a oitava dimensão, de repente encontramos o fato de que nesses espaços há espaço suficiente para espremer as esferas ali. O resultado é uma configuração extremamente simétrica chamada _de grade E ₈ . Na 24ª dimensão, uma rede de Lich surge de maneira semelhante, quando esferas adicionais podem ser amontoadas nas aberturas, criando assim outra construção bem conhecida para empacotar esferas.

Por razões não completamente compreendidas pelos matemáticos, essas duas treliças aparecem subitamente em uma área da matemática ou em outra, da teoria dos números e análise matemática à física matemática. "Não sei um motivo para tudo isso", disse Henry Cohn, do Microsoft Research New England Institute, em Cambridge, Massachusetts, um dos cinco autores do trabalho.

Por mais de dez anos, os matemáticos obtiveram evidências numéricas convincentes de que E8 e a rede de Lich são universalmente ótimas em suas dimensões - mas até recentemente eles não tinham idéia de como provar isso. Então, em 2016, Vyazovskaya deu o primeiro passo nesse sentido, provando que essas duas treliças são as melhores maneiras de embalar esferas.

E se a prova de Hales para o gabinete tridimensional se estende por centenas de páginas e requer cálculos caros no computador, a prova de Vyazovskaya para o caso do E ₈ cabe em 23 páginas. A essência de seus argumentos está ligada à definição de uma função "mágica" (como os matemáticos agora a chamam), que fornece o que Hales chamou de "certificado" para o E ₈ para o melhor empacotamento de esferas - essa prova é difícil de obter, mas após a sua aparência, ela é instantaneamente convincente. Por exemplo, se alguém lhe perguntasse se existe um número real x tal que o polinômio x ² - 6x + 9 se torne negativo, você poderia pensar na resposta. No entanto, percebendo que esse polinômio é equivalente a (x - 3) ² , você entenderia imediatamente que a resposta é "não", porque o quadrado de um número real não pode ser negativo.

O método de busca pela função mágica de Vyazovskaya provou ser poderoso - e quase poderoso demais. A tarefa de empacotar esferas diz respeito apenas à interação de pontos próximos, mas a abordagem de Vyazovskaya parecia funcionar para interações de longo alcance, como é o caso dos elétrons remotos.

Incerteza em dimensões superiores

Para mostrar que a configuração dos pontos no espaço é universalmente ótima, é necessário primeiro determinar essa universalidade. Não existe uma configuração de pontos que seja ideal para qualquer finalidade: por exemplo, quando a força da atração atua sobre os pontos, a configuração com a menor energia não é uma rede, mas uma pilha massiva na qual todos os pontos estão em um só lugar.

Vyazovskaya, Cohn e seus colegas limitaram o escopo de seu estudo à universalidade das forças repulsivas. Mais especificamente, eles consideraram forças monótonas, isto é, aquelas nas quais a repulsão se torna mais forte quando os pontos se aproximam. Essa vasta família inclui muitas das forças comuns do mundo físico. Isso inclui as leis de potência do Universo - incluindo a lei de Coulomb para partículas eletricamente carregadas e Gaussians, funções gráficas baseadas em sino que descrevem o comportamento de entidades com muitas partes repulsivas independentes, como polímeros longos. A tarefa de empacotar as esferas está na borda externa deste universo: o requisito de que as esferas não se cruzem se transforma em repulsão infinitamente forte quando a distância entre seus centros é menor que seu diâmetro.

Para qualquer uma dessas forças monótonas, surge a questão - qual será a configuração com a menor energia - o "estado fundamental" - para um conjunto infinito de partículas? Em 2006, Kon e Kumar desenvolveram um método para encontrar um limite menor de energia do estado fundamental, comparando uma função que descreve energia com funções “auxiliares” menores, com propriedades muito convenientes. Eles encontraram um suprimento infinito de funções auxiliares para cada dimensão, mas não sabiam como encontrar a melhor função auxiliar.


Cinco autores do novo trabalho: Henry Cohn, Abkhinav Kumar, Marina Vyazovskaya, Stephen Miller e Danilo Radchenko

Na maioria das medições, as limitações numéricas descobertas por Kohn e Kumar não se assemelham à energia da melhor configuração possível. Mas nas dimensões 8 e 24, os limites aproximaram-se surpreendentemente da energia E ₈ e da rede de Lich para cada força repulsiva na qual Kon e Kumar testaram seu método. Era natural pensar se, para qualquer força repulsiva, existe alguma função auxiliar ideal que daria um limite exatamente coincidente com a energia E8 ou a rede de Lich. Para a tarefa de empacotar esferas, foi exatamente isso que Vyazovskaya fez três anos atrás: ela descobriu uma função auxiliar “mágica” ideal, estudando uma classe de funções denominadas funções modulares , cujas propriedades especiais de simetria, séculos atrás, faziam delas um objeto de estudo.

Quando se tratava de outros problemas com pontos repulsivos, por exemplo, o problema com elétrons, os pesquisadores sabiam quais propriedades uma função mágica deveria satisfazer: em certos pontos, ela deveria ter valores especiais e sua transformada de Fourier , que mede as frequências naturais da função, deveria levar valores especiais em outros pontos. O que eles não sabiam era se tal função existia.

Geralmente, é bastante simples construir uma função que faça o que você precisa em seus pontos favoritos, mas é surpreendentemente difícil controlar a função e sua imagem de Fourier ao mesmo tempo. "Quando você começa a fazer algo fazer um deles, o outro faz algo completamente diferente dos seus desejos", disse Cohn.

De fato, esse mimado nada mais é do que um princípio disfarçado de incerteza na física. O princípio da incerteza de Heisenberg é que diz que quanto mais você sabe sobre a localização de uma partícula, menos você sabe sobre seu momento e vice-versa, é um caso especial desse princípio geral, porque a onda de momento da partícula é a transformada de Fourier da sua onda de localização.

No caso da força repulsiva nas dimensões 8 ou 24, Vyazovskaya apresentou uma hipótese ousada: as restrições que a equipe queria impor sobre sua função mágica e sua imagem de Fourier estão exatamente na fronteira entre o possível e o impossível. Ela suspeitava que se você adicionar mais restrições, não haveria essa função; se você reduzir as restrições, poderá haver muitas dessas funções. Ela sugeriu que, na situação que interessava à equipe, deveria haver exatamente uma função adequada.

"Acho que esse é um dos grandes recursos de Marina", disse Cohn. "Ela é muito perspicaz e também muito corajosa."

Naquela época, Kon estava cético - o palpite de Vyazovskaya parecia bom demais para ser verdade - mas a equipe acabou provando isso. Eles não apenas mostraram que para cada força repulsiva há exatamente uma função mágica, mas também deram uma receita para sua fabricação. Como no caso de esferas de empacotamento, esse projeto imediatamente forneceu certificados de otimização para o E ₈ e a rede Lich. "É um resultado monumental", disse Schwartz.

Grade triangular

Além de resolver o problema da otimização universal, uma nova prova responde à pergunta urgente que os matemáticos enfrentaram desde que Vyazovskaya resolveu o problema de empacotar esferas há três anos: de onde veio sua função mágica? "Acho que muitos ficaram intrigados", disse Vyazovskaya. "Eles perguntaram: qual é o sentido disso?"

Em um novo trabalho, Vyazovskaya e seus colegas mostraram que a função mágica de empacotar esferas é a primeira de uma série de blocos de construção de formas modulares que podem ser usadas para criar funções mágicas para cada força repulsiva. "Agora ela tem muitos irmãos e irmãs", disse Vyazovskaya.

Ainda parece maravilhoso para Kon que a imagem tenha funcionado tão bem. "Em matemática, algumas coisas precisam ser alcançadas através da perseverança e força bruta", disse ele. "E há momentos, como é agora, como se a matemática quisesse que algo acontecesse."

A próxima questão natural é se esses métodos podem ser adaptados para provar a otimização universal para o único candidato restante: reticulado de triângulos equilaterais em um plano bidimensional. Para os matemáticos, o fato de ninguém ser capaz de evidenciar em condições tão simples é considerado "uma vergonha terrível para toda a comunidade", disse Edward Saff , matemático da Universidade Vanderbilt em Nashville.

Ao contrário do E ₈ e da rede de Leach, uma rede triangular bidimensional aparece em diferentes lugares da natureza, desde estruturas celulares até a localização de funis em supercondutores. Os físicos já implicam a otimização dessa estrutura em uma ampla gama de contextos, com base em uma montanha de experimentos e simulações. Mas, diz Cohn, ninguém tem uma explicação conceitual de por que uma estrutura triangular deve ser universalmente ótima - algo que, esperançosamente, forneça prova matemática.

A dimensão 2 é a única, com exceção de 8 e 24, na qual o limite inferior numérico de Kohn e Kumar funciona bem. Isso sugere claramente que uma função mágica deve existir em duas dimensões. No entanto, o método de comando para a construção de funções mágicas dificilmente pode ser transferido para essa nova área: depende fortemente do fato de que os números que denotam as distâncias entre os pontos em E ₈ e a rede de Lich se comportam especialmente bem, o que não ocorre em duas dimensões. Até agora, essa dimensão "parece estar além das capacidades humanas", disse Cohn.

Até agora, os matemáticos estão comemorando seu novo insight associado aos mundos estranhos dos espaços 8 e 24 dimensionais. Como disse Schwartz, isso é "uma das melhores coisas que provavelmente verei na minha vida".