Um modelo de uma série natural de números e seus elementos. Rhombuses

   

Neste trabalho, o modelo básico de G ^{2 ±} é mantido, mas uma organização diferente de suas células é aceita (outra figura). No topo da rede primária com células 1 × 1 , uma grade maior é representada - uma grade de losangos e também uma grade de centros de losangos (SCR). A última grade não é representada para não sobrecarregar as linhas com o padrão com losangos. Não repetiremos as definições e conceitos que foram descritos em detalhes em trabalhos anteriores , mas forneceremos links apontando para esses trabalhos.

Descrição construtiva do modelo

Através das células modelos G ^{2 ±} contidos nas diagonais D _i longas e K _i curtas com números terminando em zeros no submodelo G ^{2 -} , são traçadas linhas que formam uma grande rede de rombos no plano. As regiões rômbicas das células cobrem coletivamente todo o plano, sem lacunas. Cada losango contém 41 células, das quais apenas 16 são de interesse e, ao investigar um losango, apenas 4 células com flexão fixa são usadas.

As características dos losangos incluem:

• o número de células no losango;
• o valor do número na célula central;
• os números de sua horizontal ( N _i ) e vertical ( V _i );
• identificar células para números com inflexões 1, 3, 7, 9;
• as coordenadas dessas células no sistema de coordenadas do losango com a origem na célula central do losango.

Uma grade de centros de losango também é construída através das células dos centros de losango, cujos nós estão localizados nas células na interseção de diagonais longas e curtas com números que são múltiplos do número 5.
A partir da figura com losangos, é claro que tipo de grade está envolvida. Para ilustrar as características dos losangos, são fornecidas imagens de um par de losangos em cada semiplano. Esses losangos são marcados com a identificação de números de células na metade inferior e outro par desses losangos nos semiplanos superiores. A marcação de losangos no semiplano abaixo da diagonal D ₀ difere da marcação de losangos no semiplano acima dele, mas dentro do mesmo semiplano, a marcação de todos os losangos é idêntica para os semiplanos superiores e inferiores. A essência da marcação é a localização de células com números com inflexões iguais (marcadas pelo preenchimento das células com a mesma cor), definindo suas coordenadas x ₁ , x ₀ . Os losangos designados serão chamados fundamentais; outros losangos com zoom podem ser formados a partir deles.

Os centros dos losangos do semiplano inferior são células com números que terminam em dois dígitos, 25 com o número horizontal com flexão 5 e com o número vertical com flexão 0 ou 75 com o número horizontal com flexão 0 e com o número vertical com flexão 5. No semiplano superior ^{2 +} - submodelos, todos os números nas células centrais de todos os losangos terminam com dois dígitos 25. Além disso, restringimos nossa consideração ao semiplano ^{2 -} .


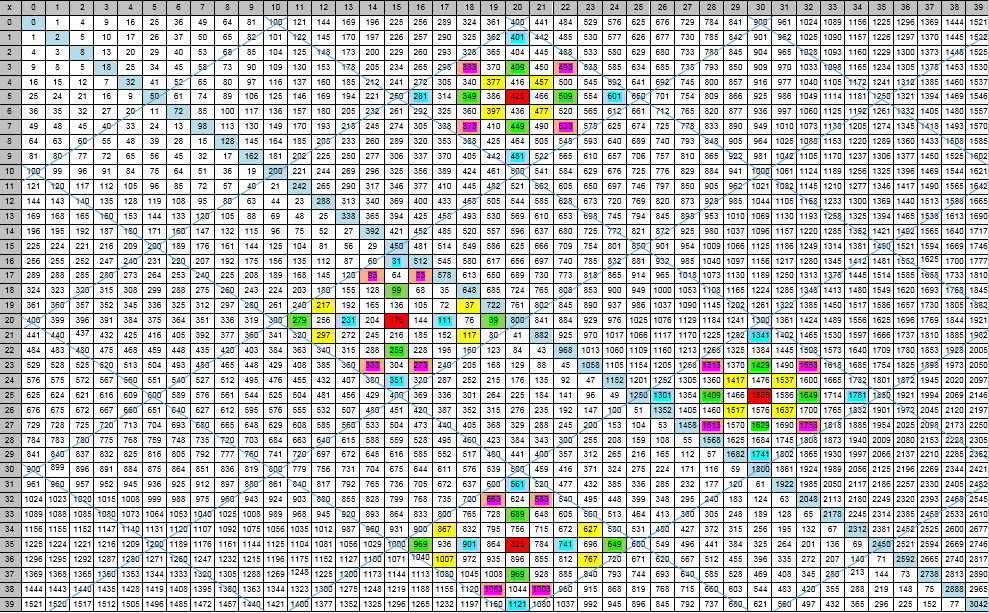_{Figura 1 - Representação visual de um modelo de diamante}

Definição 1. O losango fundamental é a estrutura do modelo ^{± 2 ±} delimitada por duas diagonais curtas e duas longas deste plano com números divisíveis pelo número 10. O elemento principal que caracteriza o losango é a célula ( x _1c , x _0c ) do seu centro. O centro contém um valor numérico de N, um múltiplo de 5.

Definição 2. O conjunto de centros de losangos fundamentais são os nós (células) da rede de centros de losangos (SCR) que cruzam diagonais curtas e longas com números que são múltiplos de 5. Os próprios losangos cobrem completamente o plano ^{2 ±} - modelos (princípio do parquet).

Todos os losangos são organizados da mesma maneira, e os números em suas células com terminações fixas são colocados em posições fixas (células). Isso permite que você fatore facilmente esse número ao resolver o problema de localizar o número N em um determinado losango. Dez horizontais cujas células formam um losango e os losangos vizinhos (com coordenadas diferentes) serão chamados de faixas de losangos. As faixas horizontais são consideradas: Oeste-Leste (); vertical: Norte-Sul (NW), ao longo de diagonais curtas: Nordeste (NE) e ao longo de diagonais longas: Noroeste (NW). O deslocamento de um losango para outro pode ser complementado por uma indicação (para cima e para baixo) ao longo das faixas indicadas, além de indicar a faixa.

Como segue da definição 2 que o conjunto de células de todos os losangos é todas as células do modelo G ^{2 ±} , em uma das células (x _1p , x _0p ) pertencentes a um determinado losango, um determinado número natural ímpar composto (ELF) N ( x _1p , x _0p ) = N (x ₁ , x ₀ ) . Ao mesmo tempo, acreditamos que é possível indicar um losango (determinando as coordenadas de sua célula central) (x _1c , x _0c ) do que investigar todas as células, limitando-se a investigar apenas diagonais ímpares.

A indicação desse losango e a célula desejada dentro dele é uma solução para o problema de localização de um determinado número N (x ₁ , x ₀ ) . Esse problema e sua solução precedem o recebimento da decisão do WFCH. O significado e o objetivo final do problema de localização é indicar em um losango para um determinado ELF N (x ₁ , x ₀ ) os valores das coordenadas da célula (x _1p , x _0p ) no modelo G ^{2 ±} , no qual existe um número coincidente com N (x ₁ , x ₀ ) .

Neste artigo, usamos o mecanismo para estabelecer a pertença de um determinado número N a um losango específico e a uma célula nele. Esse mecanismo está longe de ser o melhor, mas nos exemplos propostos ele lida com a tarefa. Os leitores são convidados a oferecer seu original ou aprimorar esse mecanismo.

Nosso mecanismo baseia-se na notável regularidade do modelo G ^{2 ±} descoberta pelo autor: a presença nas linhas horizontais com números múltiplos de cinco (e alguns outros), células com quadrados dos elementos dos triplos pitagóricos (TFP) < g, k ₁ , k ₂ > = <hipotenusa , perna ₁ , perna ₂ >. A CFT será discutida em outro trabalho.

Para simplificar as conclusões e os cálculos, precisaremos de três sistemas de coordenadas: planar, já introduzido , em rede com outros números de diagonais para o SCR (Fig. 2) e rômbico (Tabela 1), no qual o início está associado à célula do centro do losango.


<sub>Figura 2. Numeração (dupla) de diagonais curtas e
distribuição de diamantes em diagonais curtas

Tabela 1. Determinando as coordenadas de um ponto de pesquisa em um losango fixo</sub>



No sistema SCR, são indicados o seguinte: o número da diagonal curta n _p , c é o número de série do centro, bem como o número do centro C em toda a rede, sua própria numeração de diagonais curtas começando em n _p = 1 (no sistema plano é a quinta diagonal curta) , então o número n _p = 2 (este é o número aumentado em 10, ou seja, o 15º plano Ki ) e, em seguida, na etapa 10, todos os outros. A posição de todas as células dos centros de losango em cada Ki _do SCR também é numerada de c = 1 ac = 2n _{p do} número de rede duplo da diagonal curta.

Exemplo 1 Seja necessário encontrar o número C em toda a rede do centro de um dos losangos e o número N nesta célula para uma dada diagonal curta que passa pelos centros dos losangos, seu número de rede n _p = 5 e o número de série do centro c = 3 de um dos losangos nele. Simplesmente, as coordenadas de rede da célula central deste losango são representadas na forma (n _p , q) = (5, 3) .

1. Encontre a coordenada do plano x ₁ da célula no início da diagonal fornecida (nd):
   x ₁ = x _nd = 10n _p - 5 = 50 - 5 = 45.
   Para o nosso caso, obtivemos x ₁ = x _nd = 45 .
   
2. Agora podemos proceder imediatamente à busca das coordenadas planas da célula ( x _1c , x _sc ) do centro desejado: x ₁ = x _nd - 5 (c - 1) = 45 - 5 (3 - 1) = 35, x ₀ = 0 + 5 ( μ - 1) = 2 ∙ 5 = 10.
   
3. Encontre o número da rede do centro do losango ( C ).
   
   Observação. Sabe-se que para o número x a fórmula 2C _{x + 1} ² = x (x + 1) é o número duplicado de combinações de x + 1 em dois.
   O número de centros que precede a diagonal curta n _p = 5 é 2n _p (n _p - 1) . Em seguida, o número de série C do centro de rede é dado pela fórmula
   C = n _p (n _p -1) + c = 2C _{n p} ² + 3 = 5 ∙ 4 + 3 = 23 .
   
4. Encontre o valor do número N (x _1c , x _sc ) na célula do centro do losango N = x ₁ ² - x ₀ ² - o sinal na fórmula é obtido dependendo da posição do centro em relação à diagonal principal.
   N = 35 ² - 10 ² = 1125 - para o nosso caso.
   

Assim, tendo apenas o número de rede n _{p da} diagonal curta passando pelas células dos centros e o número atual do centro do losango c nessa diagonal, podemos obter todas as outras informações sobre o centro do losango.

Todos os números inteiros positivos ímpares de interesse N pertencem às células de diamante. O conceito de flexão, o último dígito de um número, permite localizar sua posição dentro de losangos. Para a fatoração, esses números N que terminam com os números 1, 3, 7, 9 são de interesse.

Os números pares não são considerados N , pois possuem um divisor principal 2. Os números que terminam com cinco têm um divisor primário 5, o que também é inaceitável para N. É recomendável localizar um N específico por inflexão dentro do losango em relação ao centro do losango, no contexto do fato de que o centro é a característica mais importante do losango. Com base no fato de que todos os losangos têm a mesma estrutura, existe uma clara relação entre o número N especificado para fatoração e os números nas células do losango com determinadas inflexões e na célula do centro do losango. Os dados sobre esses números de relacionamento são fornecidos na tabela. 1

No entanto, classificar todos os losangos em um plano para encontrar o losango desejado é inaceitável no tempo ou no custo computacional. Assim, surgiu o problema de localizar as regiões ^{2 -} - submodelos (semiplanos), incluindo losangos que conteriam o número inicial N , a ser fatorado.

Triplos pitagóricos . Para resolver o problema formulado são utilizados
Os triplos pitagóricos são triplos de números que satisfazem o teorema de Pitágoras: Nomeadamente, triplos pitagóricos que satisfazem a regra do chamado triângulo egípcio, ou seja, um triângulo com lados que são múltiplos de 3, 4, 5.
Em cada x ₁ horizontal que contém os centros de losangos, há um ou mais desses triplos pitagóricos.

O primeiro losango no problema de localização é indicado aproximadamente e, em caso de erro, os seguintes losangos devem ser selecionados. Para isso, é necessário determinar a direção do movimento ao longo do SCR, de modo a aproximar-se gradualmente do objetivo final. Por exemplo, se o menor dos 4 no losango atual de números for menor que o N fornecido, os losangos Nordeste e Leste conterão ainda menos de 4 números, ou seja, esses losangos não devem ser sondados. Mover-se para o losango ocidental leva a um aumento nos valores em todas as quatro células, que até um número menor do losango ocidental acaba sendo maior que o número maior do losango anterior e, portanto, mais que N. Daí a solução: mude do losango para o losango na direção noroeste.

Se um losango contendo uma célula com um número igual a N (x _1p , x _0p ) = N for encontrado e as coordenadas da célula (x _1p , x _0p ) forem determinadas, a solução do FBCH é determinada pela relação básica ^{2 ±} - do modelo
N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q

Outro subproblema é a seleção e implementação da sequência de desvio de células do losango selecionado para sondagem. Aqui, a ordem de rotação no sentido anti-horário é adotada, começando na célula superior esquerda que contém o número com a inflexão necessária. Em uma situação de coincidência dos valores na célula de diamante N (x _1p , x _0p ) e um determinado número N (x ₁ , x ₀ ), a diferença entre eles acaba sendo zero.

Algoritmo da solução ZFBCH usando losangos fundamentais e PFT

1. Extraímos a raiz do número N. Arredonde para baixo.
   
2. Verificamos se √N é divisível por 3. Se divisível, atribua esse valor à primeira perna k1, caso contrário, para preencher a propriedade divisibilidade por 3, subtraia 1 ou 2 do resultado e a insira na memória como k1. O resultado da divisão do valor totalmente selecionado por três M = √N / 3 - lembre-se do coeficiente de PFT da escala.
   
3. Obtemos o valor para a segunda perna k ₂ , de acordo com a regra do triângulo egípcio, k ₂ = 4 ∙ M.
   
4. Encontramos o valor da hipotenusa g = 5 ∙ M , e o valor x ₁ = g deve ser dividido pelo número cinco. Como você pode ver, o valor da hipotenusa é sempre igual ao número horizontal na TFP.
   
5. Encontre a coordenada x ₁ = g .
   
6. Depois disso, determinamos a inflexão (último dígito) do número N , φ = N (mod10) .
   
7. Encontramos o centro do losango mais próximo de k1 e, em seguida, examinamos os losangos adjacentes em uma das faixas de losangos (existem 4 direções) para encontrar uma solução.
   
8. Dependendo do tipo de inflexão que obtivermos no parágrafo 6, usamos a coluna (máscara) desejada das apresentadas na tabela. 1 para determinar as coordenadas do ponto de busca ( x _1p , x _0p ) e encontre o valor do número nesta célula N _p . Em cada losango, apenas 4 células são verificadas a partir da 41ª célula.
   
9. Depois de estabelecer que o número N pertence a um losango em particular e a uma célula, com base na mesma tabela. 1 obtemos as coordenadas do plano N: (x _1p , x _0p ) .
   
10. Usando as propriedades do modelo matemático selecionado
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q
    obtemos a representação multiplicativa de N a partir do aditivo.
    
11. Assim, na saída do algoritmo, temos: N = p ∙ q . Dependendo do valor da flexão f, de acordo com as fórmulas da tabela. 1, as coordenadas do ponto (x _1p , x _0p ) são _determinadas e a diferença ∆ = N (x _1p , x _0p ) - N (x ₁ , x ₀ ) é calculada. Se ≠ 0 , então vá para outra célula, se todas as células do losango estiverem marcadas, então para outro losango.
    Se Δ = 0 , então x ₁ = x _1p , x ₀ = x _0p ep = (x ₁ - x ₀ ) , q = N / p = (x ₁ + x ₀ ) .
    

Exemplo 2. Dado: N = 1037 , um número com capacidade de 4. É necessário fatorá-lo. Agimos de acordo com o algoritmo fornecido.

1. Extraímos a raiz de N : √N = 32.202 . Arredondamos para baixo: √N = 32 .
2. Verificamos se 32 é divisível por 3. Como 32 não é divisível por 3, subtraímos 2. Portanto, assumimos que a primeira perna é k ₁ = 3 ∙ 10 = 30 , aqui M = 10 = 30/3 é o fator de escala da PFT .
3. Obtemos o valor para a segunda etapa k ₂ = 4 ∙ 10 = 40 .
4. Encontramos o valor da hipotenusa g = (k ² ₁ + k ² ₂ ) ^0,5 , desde que seja dividido por 5, (30 ² +40 ² ) ^0,5 = 50.
5. Assim, x1 = k1 = 50 e o PFT se transforma na forma g = 50 , k ₁ = 30, k ₂ = 40 .
6. Encontramos a inflexão do número N : φ (1037) = 1037 (mod10) = 7 .
7. Encontramos o centro do losango mais próximo de N = 1037 .
   Ele terá as coordenadas da célula central do losango: x ₁ = 50, x ₀ = 35 . A primeira coordenada é o número da linha que contém a CFT. O quadrado da perna menor é 900, está contido na vertical com o número 40. A célula com o número 957 terminando com os sete mais próximos de 900 fica na horizontal anterior com o número 49 e na vertical com o número 38. Este é o menor número de 4 no losango e com inflexão 7. Aqui usamos os dados da tabela 1. O centro mais próximo do losango deve estar três células à esquerda, ou seja, pertence à vertical 38 - 3 = 35, esta é a segunda coordenada do centro do losango. O valor do número na célula do centro do losango é N (50, 35) = 1275
   
   Este é um losango com quadrados das pernas k ₁ e k ₂ em suas bordas. Dentro desse losango, min é um número que termina em sete 957 em uma célula ( x ₁ = 49, x ₀ = 38 ) e outro número nessa final vertical em 7 de 1157 , números grandes 1377 e 1577 ficam à esquerda da célula central, coincidindo com o número N = 1037 não, portanto, é necessário subir para o losango à esquerda e maior com o valor na célula central 1125 e com as coordenadas da célula central ( x ₁ = 50 - 5 = 45, x ₀ = 35 - 5 = 30 ) Verifique os quatro números para a flexão 7 Estes são 847, 1027, 1207 e 1387 e não há coincidências com N = 1037 neste losango); subiremos ainda mais na mesma direção ao longo da faixa NW de losangos. A célula central do novo losango tem um valor de 975 e coordenadas ( x ₁ = 45 -5 = 40, x ₀ = 35 - 5 = 25 ). Verificamos neste losango os quatro números da inflexão 7. Isso é 737, 897, 1197 e, finalmente, obtemos 1037 na célula ( x _1p = 39, x _0p = 22 ), conseguimos uma correspondência completa com o N.
   
   Em detalhes, essas ações são representadas pelos seguintes cálculos: De acordo com a Tabela 1, calculamos as coordenadas das células e os valores numéricos nelas. Depois disso, encontramos as diferenças entre os valores calculados e dados de N. No primeiro losango, todas as 4 células são calculadas.
   
   ∆ = N (x _1c -1, x _0c -3) - N (x ₁ , x ₀ ) = N (49,32) - 1037 = 1377 - 1037 = 340 ≠ 0,
   Como _{podemos calcular o valor de} x na _{equação ax2} + _bx + _c = ₀ , então o valor de x é :
   ∆ = N (x _1c +1, x _0c +3) - N (x ₁ , x ₀ ) = N (51,38) - 1037 = 1157 - 1037 = 120 ≠ 0,
   ∆ = N (x _1c -1, x _0c +3) - N (x ₁ , x ₀ ) = N (49,38) - 1037 = 957 - 1037 = - 80 ≠ 0.
   Nesse losango, não há coincidência do número N com os números nas células.
   
   Vamos para o próximo losango com o centro na célula (x _1c -5, x _0c -5) = (45, 30) e o valor nele N (x _1c -5, x _0c -5) = N (45, 30) = 1125 .
   ∆ = N (x _1ts -1, x _0ts -3) - N (x ₁ , x ₀ ) = N (44,27) - 1037 = 1207 - 1037 = 170 ≠ 0,
   Como _{podemos calcular o valor de} x na _{equação ax2} + _bx + _c = ₀ , então o valor de x é :
   ∆ = N (x _1c +1, x _0c +3) - N (x ₁ , x ₀ ) = N (46,33) - 1037 = 1027 - 1037 = - 10 ≠ 0,
   ∆ = N (x _1c -1, x _0c +3) - N (x ₁ , x ₀ ) = N (44,33) - 1037 = 847 - 1037 = - 190 ≠ 0.
   Nesse losango, também não há coincidência do número N com os números nas células.
   
   Vamos para o próximo losango com o centro na célula (x _1c -5, x _0c -5) = (40, 25) e o valor nele N (x _1c -5, x _0c -5) = N (40, 25) = 975
   ∆ = N (x _1c -1, x _0c -3) - N (x ₁ , x ₀ ) = N (39,22) - 1037 = 1037 - 1037 = 0.
   Tem uma diferença zero de valores. Há uma completa coincidência. Daqui resulta que o número dado N (x ₁ , x ₀ ) = 1037 está contido na célula com coordenadas (x ₁ , x ₀ ) = (39, 22) Por fim, a solução do HFBC é determinada pela relação básica ^{2 ±} - do modelo
   N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = (39 - 22) (39 + 22) = p ∙ q = 17 ∙ 61 .
   
8. Você pode agir de maneira diferente: começando com o losango indicado no parágrafo 6, usando a tabela 1, descobrimos se o número N pertence a um losango específico, movendo-se entre os centros dos losangos primeiro horizontalmente, em direção à diagonal principal, depois descendo para a próxima faixa de losangos e repetindo tudo novamente.
9. Depois de estabelecer que o número N pertence a um certo losango (no nosso caso, o losango terá coordenadas ( x ₁ = 40, x ₀ = 25 )) com base na mesma tabela. 1 obtemos as coordenadas N : x _1p = 39 , x _2p = 22 (9 losangos vistos).
10. Usando as propriedades do modelo matemático selecionado do número
    N = x ² ₁ - x ² ₀ = (x ₁ - x ₀ ) (x ₁ + x ₀ ) = p ∙ q
    obtemos a representação multiplicativa de N a partir do aditivo:
    N = (39 - 22) (39 + 22) = 17 ∙ 61 = 1037 .

Assim, na saída, temos N = p · q = 17 · 61 = 1037 , isto é, a solução para o problema foi obtida com sucesso.

Também obtemos o resultado de uma solução de software para o problema no exemplo 3.

Exemplo 3 Dado: N = 3808572773, um número com uma resolução de 10.

1. Extraímos a raiz de N: √N = 61713 , 64 = 61713 .
2. Verifique se 61713 é divisível por 3. Como 61713 é divisível por 3,
   6 + 1 + 7 + 1 + 3 = 18 é dividido por 3, então a primeira perna k ₁ é igual a k ₁ = 61713 .
3. Temos a segunda etapa k ₂ = 4k 1/3 => 4k 2/3 = 82284 .
4. Encontramos a hipotenusa g = √k ₁₂ + k ₂₂ , desde que seja dividida por
   5 g = √617132 + 822842 = 102855 .
5. Assim, x ₁ = k ₁ = 61713 e o triplo pitagórico se transforma, respectivamente, na forma k ₁ = 61713, k ₂ = 82284, g = 102855 .
6. N: (3808572773) = 3808572773(mod10) = 3 .
7. . x ₁ = 61715; x ₉ = 0 .
8. , 7, . 1, N , , , , .
9. N ( x ₁ = 62015 , x ₀ = 6085 ) N :
   x _1p = 62013; x _0p = 6086 ; ( 60 ).
10. 
    N = x ² ₁ — x ² ₀ = (x ₁ — x ₀ )(x ₁ + x ₀ ) =p ·q N :
    N = (62013 — 6086) · (62013 + 62086) = 55927 · 68099 = 3808572773 ;
11. , N = p · q = 55927 · 68099 = 3808572773 , . . .