Imagine que você precise gerar um número aleatório uniformemente distribuído de 1 a 10. Ou seja, um número inteiro de 1 a 10 inclusive, com uma probabilidade igual (10%) de cada ocorrência. Mas, digamos, sem acesso a moedas, computadores, material radioativo ou outras fontes semelhantes de (pseudo) números aleatórios. Você só tem um quarto com pessoas.

Suponha que haja pouco mais de 8500 estudantes nesta sala.

O mais simples é perguntar a alguém: “Ei, escolha um número aleatório de um a dez!”. O homem responde: "Sete!". Ótimo! Agora você tem um número. No entanto, você começa a se perguntar se é distribuído igualmente.

Então você decidiu pedir mais algumas pessoas. Você continua perguntando a eles e contando suas respostas, arredondando os números fracionários e ignorando aqueles que pensam que o intervalo de 1 a 10 inclui 0. No final, você começa a ver que a distribuição não é de todo:

library(tidyverse) probabilities <- read_csv("https://git.io/fjoZ2") %>% count(outcome = round(pick_a_random_number_from_1_10)) %>% filter(!is.na(outcome), outcome != 0) %>% mutate(p = n / sum(n)) probabilities %>% ggplot(aes(x = outcome, y = p)) + geom_col(aes(fill = as.factor(outcome))) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = '"Pick a random number from 1-10"', subtitle = "Human RNG distribution", x = "", y = NULL, caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/") 

Dados do Reddit

Você bate na sua testa. Bem, é claro , não será aleatório. Afinal, você não pode confiar nas pessoas .

Então o que fazer?

Eu gostaria de encontrar alguma função que transforma a distribuição do "RNG humano" em uma distribuição uniforme ...

A intuição aqui é relativamente simples. Você só precisa pegar a massa de distribuição de onde está acima de 10% e movê-la para onde está abaixo de 10%. Para que todas as colunas no gráfico estejam no mesmo nível:



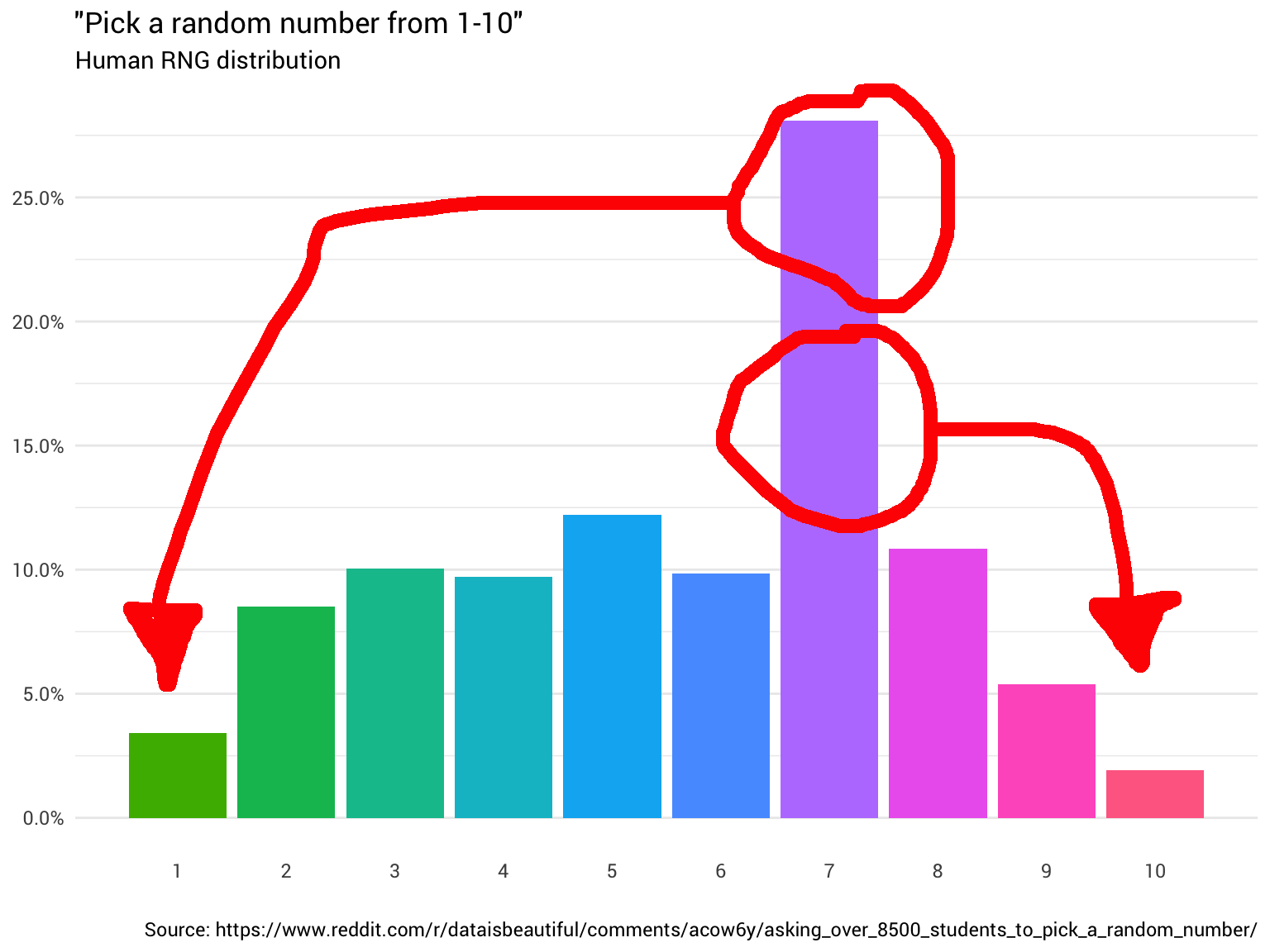
Em teoria, essa função deveria existir. De fato, deve haver muitas funções diferentes (para permutação). Em um caso extremo, você pode "cortar" cada coluna em blocos infinitamente pequenos e criar uma distribuição de qualquer forma (como tijolos de Lego).

Obviamente, um exemplo tão extremo é um pouco complicado. Idealmente, queremos manter o máximo possível da distribuição inicial (ou seja, fazer o menor número possível de fragmentos e movimentos).

Como encontrar essa função?

Bem, nossa explicação acima parece muito com programação linear . Da Wikipedia:

A programação linear (LP, também chamada de otimização linear) é um método para obter o melhor resultado ... em um modelo matemático cujos requisitos são representados por relações lineares ... O formulário padrão é a forma mais usual e intuitiva de descrever um problema de programação linear. Consiste em três partes:

• Função linear a ser maximizada
  
• Limitações do problema do seguinte formulário
  
• Variáveis ​​não negativas

Da mesma forma, o problema da redistribuição pode ser formulado.

Apresentação do problema

Temos um conjunto de variáveis $$$(x_ {i, j}$ , cada um dos quais codifica uma fração da probabilidade redistribuída de um número inteiro $$$i$ (1 a 10) em um número inteiro $$$j$ (de 1 a 10). Portanto, se $$$(x_ {7,1} = 0,2$ , precisamos transferir 20% das respostas de sete para um.

 variables <- crossing(from = probabilities$outcome, to = probabilities$outcome) %>% mutate(name = glue::glue("x({from},{to})"), ix = row_number()) variables 

  ## # Uma porção: 100 x 4
 ## de para nomear ix
 ## <dbl> <dbl> <cola> <int>
 ## 1 1 1 x (1,1) 1
 ## 2 1 2 x (1,2) 2
 ## 3 1 3 x (1,3) 3
 ## 4 1 4 x (1,4) 4
 ## 5 1 5 x (1,5) 5
 ## 6 1 6 x (1,6) 6
 ## 7 1 7 x (1,7) 7
 ## 8 1 8 x (1,8) 8
 ## 9 1 9 x (1,9) 9
 ## 10 1 10 x (1,10) 10
 ## # ... com mais 90 linhas 

Queremos limitar essas variáveis ​​para que todas as probabilidades redistribuídas atinjam 10%. Em outras palavras, para cada $$$j$ de 1 a 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0,1$$

Podemos representar essas restrições como uma lista de matrizes em R. Mais tarde, as vinculamos a uma matriz.

 fill_array <- function(indices, weights, dimensions = c(1, max(variables$ix))) { init <- array(0, dim = dimensions) if (length(weights) == 1) { weights <- rep_len(1, length(indices)) } reduce2(indices, weights, function(a, i, v) { a[1, i] <- v a }, .init = init) } constrain_uniform_output <- probabilities %>% pmap(function(outcome, p, ...) { x <- variables %>% filter(to == outcome) %>% left_join(probabilities, by = c("from" = "outcome")) fill_array(x$ix, x$p) }) 

Também devemos garantir que toda a massa de probabilidades da distribuição inicial seja preservada. Então, para todos $$$j$ no intervalo de 1 a 10:

$$

$$x_ {1, j} + x_ {2, j} + \ ldots \ x_ {10, j} = 0,1$$

 one_hot <- partial(fill_array, weights = 1) constrain_original_conserved <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome) %>% pull(ix) %>% one_hot() }) 

Como já mencionado, queremos maximizar a preservação da distribuição original. Este é o nosso objetivo :

$$

$$maximizar (x_ {1, 1} + x_ {2, 2} + \ ldots \ x_ {10, 10})$$

 maximise_original_distribution_reuse <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome, to == outcome) %>% pull(ix) %>% one_hot() }) objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums() 

Depois, passamos o problema para o solucionador, por exemplo, o pacote lpSolve no R, combinando as restrições criadas em uma matriz:

 # Make results reproducible... set.seed(23756434) solved <- lpSolve::lp( direction = "max", objective.in = objective, const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)), const.dir = c(rep_len("==", length(constrain_original_conserved)), rep_len("==", length(constrain_uniform_output))), const.rhs = c(rep_len(1, length(constrain_original_conserved)), rep_len(1 / nrow(probabilities), length(constrain_uniform_output))) ) balanced_probabilities <- variables %>% mutate(p = solved$solution) %>% left_join(probabilities, by = c("from" = "outcome"), suffix = c("_redistributed", "_original")) 

A seguinte redistribuição é retornada:

 library(gganimate) redistribute_anim <- bind_rows(balanced_probabilities %>% mutate(key = from, state = "Before"), balanced_probabilities %>% mutate(key = to, state = "After")) %>% ggplot(aes(x = key, y = p_redistributed * p_original)) + geom_col(aes(fill = as.factor(from)), position = position_stack()) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = 'Balancing the "Human RNG distribution"', subtitle = "{closest_state}", x = "", y = NULL) + transition_states( state, transition_length = 4, state_length = 3 ) + ease_aes('cubic-in-out') animate( redistribute_anim, start_pause = 8, end_pause = 8 ) 

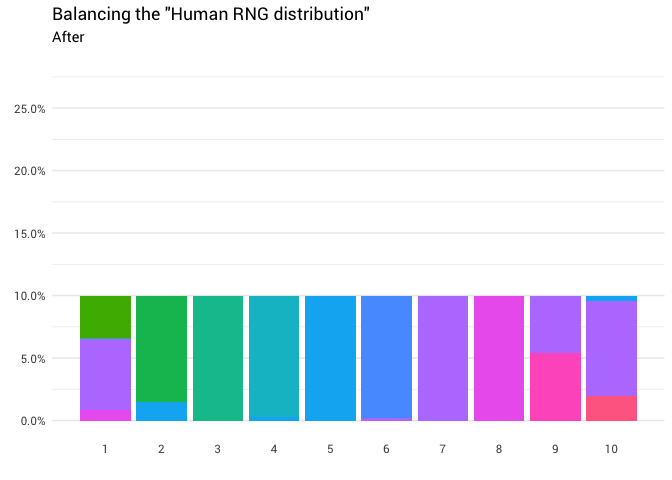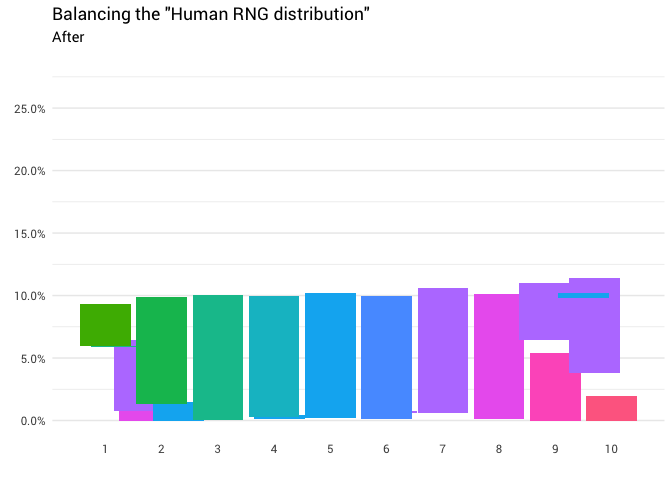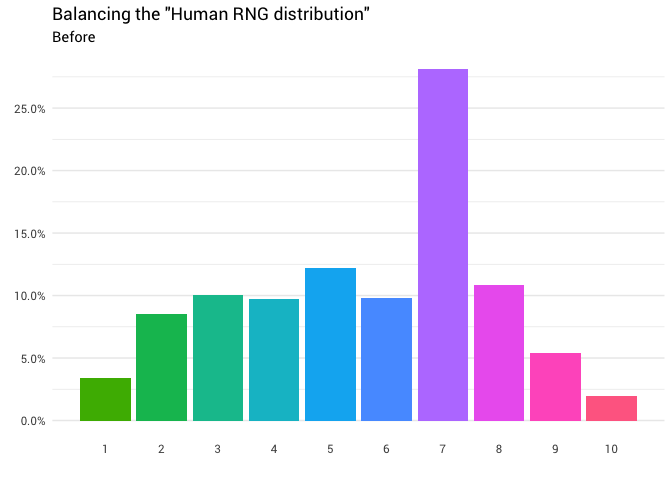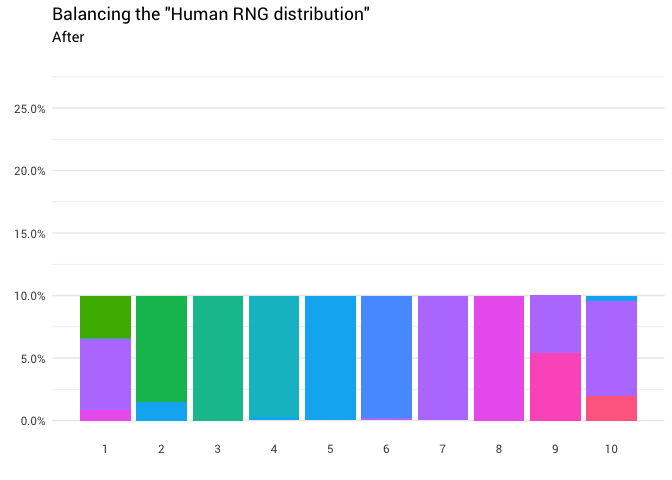
Ótimo! Agora temos uma função de redistribuição. Vamos examinar mais de perto exatamente como a massa se move:

 balanced_probabilities %>% ggplot(aes(x = from, y = to)) + geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) + geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) + scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) + scale_fill_discrete(h = c(120, 360)) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(breaks = 1:10) + theme_minimal(base_family = "Roboto") + theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(linetype = "dotted"), legend.position = "none") + labs(title = "Probability mass redistribution", x = "Original number", y = "Redistributed number") 

Este gráfico diz que em cerca de 8% dos casos, quando alguém liga para oito como um número aleatório, você precisa tomar a resposta como uma unidade. Nos restantes 92% dos casos, ele continua sendo o oito.

Seria bastante simples resolver o problema se tivéssemos acesso a um gerador de números aleatórios distribuídos igualmente (de 0 a 1). Mas só temos uma sala cheia de pessoas. Felizmente, se você estiver pronto para lidar com algumas pequenas imprecisões, poderá criar um RNG bastante bom sem precisar pedir mais do que duas vezes.

Voltando à nossa distribuição original, temos as seguintes probabilidades para cada número, que podem ser usadas para reatribuir qualquer probabilidade, se necessário.

 probabilities %>% transmute(number = outcome, probability = scales::percent(p)) 

  ## # Um toque: 10 x 2
 ## probabilidade de número
 ## <dbl> <chr>
 1 3,4%
 # 2 2 8,5%
 ## 3 3 10,0%
 ## 4 4 9,7%
 ## 5 5 12,2%
 ## 6 6 9,8%
 ## 7 7 28,1%
 ## 8 8 10,9%
 ## 9 9 5,4%
 ## 10 10 1,9% 

Por exemplo, quando alguém nos dá oito como um número aleatório, precisamos determinar se esses oito devem se tornar uma unidade ou não (probabilidade 8%). Se perguntarmos a outra pessoa um número aleatório, com uma probabilidade de 8,5%, ela responderá "dois". Portanto, se esse segundo número for 2, sabemos que devemos retornar 1 como um número aleatório distribuído uniformemente .

Estendendo essa lógica a todos os números, obtemos o seguinte algoritmo:

• Peça a uma pessoa um número aleatório, $$$n_1$ .
• $$$n_1 = 1, 2, 3, 4, 6, 9,$ ou $$$10$ :
  
  • Seu número aleatório $$$n_1$
• Se $$$n_1 = 5$ :
  
  • Peça a outra pessoa um número aleatório ( $$$n_2$ )
  • Se $$$n_2 = 5$ (12,2%):
    
    • Seu número aleatório 2
  • Se $$$n_2 = 10$ (1,9%):
    
    • Seu número aleatório 4
  • Caso contrário, seu número aleatório é 5
• Se $$$n_1 = 7$ :
  
  • Peça a outra pessoa um número aleatório ( $$$n_2$ )
  • Se $$$n_2 = 2$ ou $$$5$ (20,7%):
    
    • O seu número aleatório 1
  • Se $$$n_2 = 8$ ou $$$9$ (16,2%):
    
    • Seu número aleatório é 9
  • Se $$$n_2 = 7$ (28,1%):
    
    • Seu número aleatório é 10
  • Caso contrário, seu número aleatório é 7
• Se $$$n_1 = 8$ :
  
  • Peça a outra pessoa um número aleatório ( $$$n_2$ )
  • Se $$$n_2 = 2$ (8,5%):
    
    • O seu número aleatório 1
  • Caso contrário, seu número aleatório é 8

Usando esse algoritmo, você pode usar um grupo de pessoas para obter algo próximo a um gerador de números aleatórios distribuídos uniformemente de 1 a 10!