Redes neurais e aprendizado profundo, capítulo 3, parte 2: por que a regularização ajuda a reduzir o treinamento?

Empiricamente, vimos que a regularização ajuda a reduzir a reciclagem. Isso é inspirador - mas, infelizmente, não é óbvio por que a regularização ajuda. Geralmente, as pessoas explicam de alguma maneira: em certo sentido, pesos menores têm menos complexidade, o que fornece uma explicação mais simples e eficiente dos dados, portanto, eles devem ser os preferidos. No entanto, essa é uma explicação muito curta e algumas partes dela podem parecer dúbias ou misteriosas. Vamos desdobrar esta história e examiná-la com um olhar crítico. Para fazer isso, suponha que tenhamos um conjunto de dados simples para o qual queremos criar um modelo:


Em termos de significado, aqui estudamos o fenômeno do mundo real, e x e y denotam dados reais. Nosso objetivo é construir um modelo que nos permita prever y em função de x. Poderíamos tentar usar uma rede neural para criar esse modelo, mas sugiro algo mais simples: tentarei modelar y como um polinômio em x. Farei isso em vez de redes neurais, pois o uso de polinômios torna a explicação especialmente clara. Assim que lidarmos com o caso do polinômio, passaremos para a Assembléia Nacional. Existem dez pontos no gráfico acima, o que significa que podemos encontrar um polinômio exclusivo de 9ª ordem y = a ₀ x ⁹ + a ₁ x ⁸ + ... + a ₉ que se ajusta exatamente aos dados. E aqui está o gráfico desse polinômio.


Acerto perfeito. Mas podemos obter uma boa aproximação usando o modelo linear y = 2x


Qual é o melhor? Qual é mais provável de ser verdade? Qual será melhor generalizado para outros exemplos do mesmo fenômeno do mundo real?

Perguntas difíceis. E eles não podem ser respondidos exatamente sem informações adicionais sobre o fenômeno subjacente do mundo real. Contudo, vejamos duas possibilidades: (1) um modelo com um polinômio de 9ª ordem realmente descreve o fenômeno do mundo real e, portanto, generaliza perfeitamente; (2) o modelo correto é y = 2x, mas temos ruído adicional associado ao erro de medição; portanto, o modelo não se encaixa perfeitamente.

A priori, não se pode dizer qual das duas possibilidades está correta (ou que não existe uma terceira). Logicamente, qualquer um deles pode se tornar verdadeiro. E a diferença entre eles é não trivial. Sim, com base nos dados disponíveis, pode-se dizer que há apenas uma pequena diferença entre os modelos. Mas suponha que desejamos prever o valor de y correspondente a algum valor grande de x, muito maior que qualquer um dos mostrados no gráfico. Se tentarmos fazer isso, uma enorme diferença aparecerá entre as previsões dos dois modelos, já que o termo x ⁹ domina no polinômio de 9ª ordem, e o modelo linear permanece linear.

Um ponto de vista do que está acontecendo é afirmar que uma explicação mais simples deve ser usada na ciência, se possível. Quando encontramos um modelo simples que explica muitos pontos de referência, queremos apenas gritar: "Eureka!" Afinal, é improvável que uma explicação simples apareça puramente por acidente. Suspeitamos que o modelo deva produzir alguma verdade associada ao fenômeno. Nesse caso, o modelo y = 2x + ruído parece muito mais simples que y = a ₀ x ⁹ + a ₁ x ⁸ + ... Seria surpreendente se a simplicidade surgisse por acaso, portanto suspeitamos que y = 2x + ruído expresse alguma verdade subjacente. Desse ponto de vista, o modelo de 9ª ordem simplesmente estuda o efeito do ruído local. Embora o modelo de 9ª ordem funcione perfeitamente para esses pontos de referência específicos, ele não pode generalizar para outros pontos, como resultado do qual o modelo linear com ruído terá melhores recursos preditivos.

Vamos ver o que esse ponto de vista significa para redes neurais. Suponha que, em nossa rede, haja principalmente pesos baixos, como é geralmente o caso em redes regularizadas. Devido ao seu pequeno peso, o comportamento da rede não muda muito quando várias entradas aleatórias são alteradas aqui e ali. Como resultado, a rede regularizada é difícil de aprender os efeitos do ruído local presente nos dados. Isso é semelhante ao desejo de garantir que as evidências individuais não afetem grandemente a saída da rede como um todo. Em vez disso, a rede regularizada é treinada para responder às evidências frequentemente encontradas nos dados de treinamento. Por outro lado, uma rede com grandes pesos pode mudar seu comportamento bastante fortemente em resposta a pequenas alterações nos dados de entrada. Portanto, uma rede irregular pode usar grandes pesos para treinar um modelo complexo que contém muitas informações de ruído nos dados de treinamento. Em resumo, as limitações das redes regularizadas permitem que eles criem modelos relativamente simples com base em padrões frequentemente encontrados nos dados de treinamento e são resistentes a desvios causados ​​por ruído nos dados de treinamento. Há uma esperança de que isso faça com que nossas redes estudem o fenômeno em si e generalizem melhor o conhecimento adquirido.

Com tudo isso dito, a idéia de dar preferência a explicações mais simples deve deixá-lo nervoso. Às vezes, as pessoas chamam essa idéia de "navalha de Occam" e a aplicam com zelo, como se tivesse o status de um princípio científico geral. Mas isso, é claro, não é um princípio científico geral. Não existe uma razão lógica prioritária para preferir explicações simples a explicações complexas. Às vezes, uma explicação mais complicada está correta.

Deixe-me descrever dois exemplos de como uma explicação mais complexa se mostrou correta. Na década de 1940, o físico Marcel Shane anunciou a descoberta de uma nova partícula. A empresa para a qual ele trabalhou, General Electric, ficou encantada e distribuiu amplamente a publicação deste evento. No entanto, o físico Hans Bethe era cético. Bethe visitou Shane e estudou as placas com traços da nova partícula de Shane. Shane mostrou placa Beta após placa, mas Bete encontrou em cada um deles um problema que indicava a necessidade de recusar esses dados. Finalmente, Shane mostrou a Beta um registro que parecia adequado. Bethe disse que provavelmente era apenas um desvio estatístico. Shane: "Sim, mas as chances de isso ocorrer devido às estatísticas, mesmo pela sua própria fórmula, são de uma em cinco". Bethe: "No entanto, eu já olhei para cinco registros." Por fim, Shane disse: "Mas você explicou cada um dos meus registros, toda boa imagem com alguma outra teoria, e eu tenho uma hipótese que explica todos os registros de uma só vez, e daí resulta que estamos falando de uma nova partícula". Bethe respondeu: “A única diferença entre minhas explicações e a sua é que as suas estão erradas e as minhas estão corretas. Sua única explicação está incorreta e todas as minhas explicações estão corretas. Posteriormente, descobriu-se que a natureza concordava com Bethe, e a partícula de Shane evaporou.

No segundo exemplo, em 1859, o astrônomo Urbain Jean Joseph Le Verrier descobriu que a forma da órbita de Mercúrio não corresponde à teoria da gravitação universal de Newton. Houve um pequeno desvio dessa teoria e, em seguida, foram propostas várias opções para resolver o problema, que se resumiram ao fato de que a teoria de Newton como um todo está correta e requer apenas uma pequena alteração. E em 1916, Einstein mostrou que esse desvio pode ser bem explicado usando sua teoria geral da relatividade, radicalmente diferente da gravidade newtoniana e baseada em matemática muito mais complexa. Apesar dessa complexidade adicional, é geralmente aceito hoje que a explicação de Einstein está correta, e a gravidade newtoniana está incorreta mesmo de forma modificada . Isso acontece, em particular, porque hoje sabemos que a teoria de Einstein explica muitos outros fenômenos com os quais a teoria de Newton teve dificuldades. Além disso, o mais surpreendente é que a teoria de Einstein prediz com precisão vários fenômenos que a gravidade newtoniana não previu de maneira alguma. No entanto, essas qualidades impressionantes não eram óbvias no passado. A julgar com base na mera simplicidade, então alguma forma modificada da teoria newtoniana pareceria mais atraente.

Três moralidades podem ser extraídas dessas histórias. Primeiro, às vezes é bastante difícil decidir qual das duas explicações será "mais fácil". Em segundo lugar, mesmo que tenhamos tomado essa decisão, a simplicidade deve ser guiada com muito cuidado! Terceiro, o verdadeiro teste do modelo não é a simplicidade, mas quão bem ele prediz novos fenômenos em novas condições de comportamento.

Considerando tudo isso e tendo cuidado, aceitaremos um fato empírico - os SNs regularizados geralmente são mais generalizados do que os irregulares. Portanto, mais adiante neste livro, frequentemente usaremos a regularização. As histórias mencionadas são necessárias apenas para explicar por que ninguém ainda desenvolveu uma explicação teórica completamente convincente sobre por que a regularização ajuda as redes a generalizar. Os pesquisadores continuam publicando trabalhos nos quais tentam abordagens diferentes para regularização, comparando-os, analisando o que funciona melhor e tentando entender por que abordagens diferentes funcionam pior ou melhor. Portanto, a regularização pode ser tratada como uma nuvem . Quando isso ajuda com frequência, não temos uma compreensão sistêmica completamente satisfatória do que está acontecendo - apenas regras heurísticas e práticas incompletas.

Aqui reside um conjunto mais profundo de problemas que chegam ao coração da ciência. Este é um problema de generalização. A regularização pode nos dar uma varinha mágica computacional que ajuda nossas redes a generalizar melhor os dados, mas não fornece um entendimento básico de como a generalização funciona e qual é a melhor abordagem para ela.

Esses problemas remontam ao problema da indução , cuja interpretação bem conhecida foi realizada pelo filósofo escocês David Hume no livro " Um estudo sobre cognição humana " (1748). O problema da indução é o tema do “ teorema da ausência de refeições gratuitas ” de David Walpert e William Macredie (1977).

E isso é especialmente irritante, porque na vida comum as pessoas são fenomenalmente capazes de generalizar dados. Mostre algumas imagens do elefante à criança, e ele aprenderá rapidamente a reconhecer outros elefantes. É claro que ele às vezes pode cometer um erro, por exemplo, confundir um rinoceronte com um elefante, mas, em geral, esse processo funciona surpreendentemente com precisão. Agora, temos um sistema - o cérebro humano - com uma enorme quantidade de parâmetros livres. E depois que ele recebe uma ou mais imagens de treinamento, o sistema aprende a generalizá-las para outras imagens. Nosso cérebro, em certo sentido, é incrivelmente bom em regularizar! Mas como fazemos isso? No momento, isso é desconhecido para nós. Penso que, no futuro, desenvolveremos tecnologias de regularização mais poderosas em redes neurais artificiais, técnicas que finalmente permitirão à Assembléia Nacional generalizar dados com base em conjuntos de dados ainda menores.

De fato, nossas redes já estão generalizando muito melhor do que se poderia esperar a priori. Uma rede com 100 neurônios ocultos possui quase 80.000 parâmetros. Temos apenas 50.000 imagens em dados de treinamento. É o mesmo que tentar esticar um polinômio de 80.000 pedidos para mais de 50.000 pontos de referência. Por todas as indicações, nossa rede deve treinar muito. E, no entanto, como vimos, essa rede realmente generaliza bastante. Por que isso está acontecendo? Isto não está totalmente claro. Foi levantada a hipótese de que "a dinâmica da aprendizagem por descida gradiente em redes multicamadas está sujeita à auto-regulação". É uma fortuna extrema, mas também um fato bastante perturbador, pois não entendemos por que isso acontece. Enquanto isso, adotaremos uma abordagem pragmática e usaremos a regularização sempre que possível. Isso será benéfico para nossa Assembléia Nacional.

Deixe-me terminar esta seção, voltando ao que não expliquei antes: que a regularização de L2 não limita os deslocamentos. Naturalmente, seria fácil alterar o procedimento de regularização para regularizar os deslocamentos. Mas, empiricamente, isso geralmente não altera os resultados de maneira perceptível; portanto, até certo ponto, lidar com a regularização de vieses, ou não, é uma questão de concordância. No entanto, vale a pena notar que um grande deslocamento não torna um neurônio sensível a entradas como pesos grandes. Portanto, não precisamos nos preocupar com grandes compensações que permitam que nossas redes aprendam o ruído nos dados de treinamento. Ao mesmo tempo, ao permitir grandes deslocamentos, tornamos nossas redes mais flexíveis em seu comportamento - em particular, grandes deslocamentos facilitam a saturação dos neurônios, da qual gostaríamos. Por esse motivo, geralmente não incluímos compensações na regularização.

Outras técnicas de regularização

Existem muitas técnicas de regularização além de L2. De fato, tantas técnicas já foram desenvolvidas que, com todo o desejo, eu não conseguia descrever brevemente todas elas. Nesta seção, descreverei brevemente três outras abordagens para reduzir a reciclagem: regularizar L1, desistir e aumentar artificialmente o conjunto de treinamento. Não os estudaremos tão profundamente quanto os tópicos anteriores. Em vez disso, apenas os conhecemos e, ao mesmo tempo, apreciamos a variedade de técnicas de regularização existentes.

Regularização L1

Nesta abordagem, modificamos a função de custo irregular adicionando a soma dos valores absolutos dos pesos:

$$

$$C = C_0 + \ frac {\ lambda} {n} \ sum_w | w | \ tag {95}$$

Intuitivamente, isso é semelhante à regularização de L2, que multas por grandes pesos e faz a rede preferir pesos baixos. Obviamente, o termo de regularização L1 não é como o termo de regularização L2, portanto, você não deve esperar exatamente o mesmo comportamento. Vamos tentar entender como o comportamento de uma rede treinada com regularização L1 difere de uma rede treinada com regularização L2.

Para fazer isso, observe as derivadas parciais da função de custo. Diferenciando (95), obtemos:

$$

$$\ frac {\ parcial C} {\ parcial w} = \ frac {\ parcial C_0} {\ parcial w} + \ frac {\ lambda} {n} \, {\ rm sgn} (w) \ tag {96 }$$

onde sgn (w) é o sinal de w, ou seja, +1 se w for positivo e -1 se w for negativo. Usando esta expressão, modificamos levemente a propagação reversa para que ela execute a descida do gradiente estocástico usando a regularização L1. A regra de atualização final para a rede regularizada L1:

$$

$$w \ rightarrow w '= w- \ frac {\ eta \ lambda} {n} \ mbox {sgn} (w) - \ eta \ frac {\ C_0 parcial} {\ parcial w} \ tag {97}$$

onde, como sempre, ∂C / ∂w pode opcionalmente ser estimado usando o valor médio do minipacote. Compare isso com a regra de atualização de regularização L2 (93):

$$

$$w \ rightarrow w '= w \ left (1 - \ frac {\ eta \ lambda} {n} \ right) - \ eta \ frac {\ C_0 parcial} {\ parcial w} \ tag {98}$$

Nas duas expressões, o efeito da regularização é reduzir pesos. Isso coincide com a noção intuitiva de que ambos os tipos de regularização penalizam grandes pesos. No entanto, os pesos são reduzidos de maneiras diferentes. Na regularização de L1, os pesos diminuem em um valor constante, tendendo a 0. Na regularização de L2, os pesos diminuem em um valor proporcional a w. Portanto, quando algum peso tem um grande valor | w |, a regularização de L1 reduz o peso não tanto quanto L2. E vice-versa, quando | w | pequena, a regularização de L1 reduz o peso muito mais do que a regularização de L2. Como resultado, a regularização de L1 tende a concentrar os pesos da rede em um número relativamente pequeno de vínculos de alta importância, enquanto outros pesos tendem a zero.

Eu suavizei levemente um problema na discussão anterior - a derivada parcial ∂C / ∂w não é definida quando w = 0. Isso ocorre porque a função | w | existe uma “torção” aguda no ponto w = 0, portanto, não pode ser diferenciada lá. Mas isso não é assustador. Apenas aplicamos a regra irregular usual para a descida do gradiente estocástico quando w = 0. Intuitivamente, não há nada de errado nisso - a regularização deve reduzir pesos e, obviamente, não pode reduzir pesos já iguais a 0. Mais precisamente, usaremos as equações (96) e (97) com a condição de que sgn (0) = 0 Isso nos dará uma regra conveniente e compacta para a descida do gradiente estocástico com regularização L1.

Exceção [desistência]

Uma exceção é uma técnica de regularização completamente diferente. Diferentemente da regularização de L1 e L2, a exceção não trata de uma alteração na função de custo. Em vez disso, estamos mudando a própria rede. Deixe-me explicar a mecânica básica da operação de uma exceção antes de aprofundar o tópico sobre por que ela funciona e com quais resultados.

Suponha que estamos tentando treinar uma rede:


Em particular, digamos que tenhamos a entrada de treinamento xe a saída desejada correspondente y. Normalmente, treinávamos isso distribuindo x diretamente pela rede e depois propagando novamente para determinar a contribuição do gradiente. Uma exceção modifica esse processo. Começamos removendo aleatoriamente e temporariamente metade dos neurônios ocultos na rede, deixando os neurônios de entrada e saída inalterados. Depois disso, teremos aproximadamente essa rede. Observe que os neurônios excluídos, aqueles que são removidos temporariamente, ainda estão marcados no diagrama:


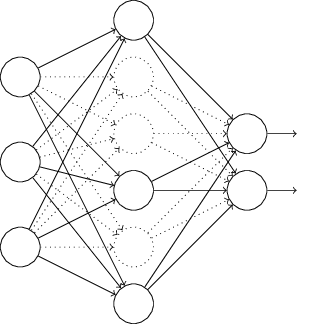
Passamos x pela distribuição direta pela rede alterada e depois distribuímos o resultado, também pela rede alterada. Depois de fazer isso com um mini-pacote de exemplos, atualizamos os pesos e compensações correspondentes. Em seguida, repetimos esse processo, restaurando primeiro os neurônios excluídos e, em seguida, escolhendo um novo subconjunto aleatório de neurônios ocultos para remover, avaliar o gradiente para outro minipacote e atualizar os pesos e compensações da rede.

Repetindo esse processo repetidamente, obtemos uma rede que aprendeu alguns pesos e deslocamentos. Naturalmente, esses pesos e deslocamentos foram aprendidos sob condições nas quais metade dos neurônios ocultos foram excluídos.E quando lançarmos a rede por completo, teremos o dobro de neurônios ocultos ativos. Para compensar isso, reduzimos pela metade os pesos provenientes dos neurônios ocultos.

O procedimento de exclusão pode parecer estranho e arbitrário. Por que ela deveria ajudar na regularização? Para explicar o que está acontecendo, quero que você esqueça a exceção por um tempo e apresente o treinamento da Assembléia Nacional de maneira padrão. Em particular, imagine que treinamos vários NS diferentes usando os mesmos dados de treinamento. Obviamente, as redes podem variar no início e, às vezes, o treinamento pode produzir resultados diferentes. Nesses casos, poderíamos aplicar algum tipo de esquema de média ou votação para decidir qual dos produtos aceitar. Por exemplo, se treinamos cinco redes, e três delas classificam o número como "3", então provavelmente são as três verdadeiras. E as outras duas redes provavelmente estão erradas. Esse esquema de média é geralmente uma maneira útil (embora cara) de reduzir a reciclagem. A razão éque redes diferentes podem ser treinadas de maneiras diferentes, e a média pode ajudar a eliminar essa reciclagem.

Como tudo isso se relaciona com a exceção? Heuristicamente, quando excluímos diferentes conjuntos de nêutrons, é como se estivéssemos treinando diferentes SNs. Portanto, o procedimento de exclusão é semelhante à média dos efeitos em um número muito grande de redes diferentes. Redes diferentes são treinadas de maneiras diferentes, portanto, espera-se que o efeito médio da exclusão reduza a reciclagem.

Uma explicação heurística relacionada dos benefícios da exclusão é apresentada em um dos primeiros trabalhosusando esta técnica: “Essa técnica reduz a complexa adaptação articular dos neurônios, porque o neurônio não pode contar com a presença de certos vizinhos. No final, ele precisa aprender características mais confiáveis ​​que possam ser úteis no trabalho em conjunto com muitos subconjuntos aleatórios diferentes de neurônios. ” Em outras palavras, se imaginarmos nossa Assembléia Nacional como um modelo que faz previsões, uma exceção será uma maneira de garantir a estabilidade do modelo à perda de partes individuais da evidência. Nesse sentido, a técnica se assemelha às regularizações de L1 e L2, que buscam reduzir pesos e, dessa forma, tornam a rede mais resistente à perda de qualquer conexão individual na rede.

Naturalmente, a verdadeira medida da utilidade da exclusão é seu tremendo sucesso em melhorar a eficiência das redes neurais. No trabalho originalonde esse método foi introduzido, foi aplicado a muitas tarefas diferentes. Estamos particularmente interessados ​​no fato de os autores aplicarem a exceção à classificação dos números do MNIST, usando uma rede de distribuição direta simples semelhante à que examinamos. O artigo observa que, até então, o melhor resultado para essa arquitetura era 98,4% de precisão. Eles melhoraram para 98,7% usando uma combinação de exclusão e uma forma modificada de regularização L2. Resultados igualmente impressionantes foram obtidos para muitas outras tarefas, incluindo reconhecimento de padrões e fala e processamento de linguagem natural. A exceção foi especialmente útil no treinamento de grandes redes profundas, onde o problema de reciclagem geralmente surge.

Conjunto de dados de treinamento em expansão artificial

Vimos anteriormente que nossa precisão na classificação MNIST caiu para 80%, quando usamos apenas 1.000 imagens de treinamento. E não é de admirar - com menos dados, nossa rede encontrará menos opções para escrever números por pessoas. Vamos tentar treinar nossa rede de 30 neurônios ocultos, usando diferentes volumes do conjunto de treinamento para observar a mudança na eficiência. Treinamos usando o tamanho de minipacote 10, a velocidade de aprendizado η = 0,5, o parâmetro de regularização λ = 5,0 e a função de custo com entropia cruzada. Treinaremos uma rede de 30 eras usando um conjunto completo de dados e aumentaremos o número de eras proporcionalmente à diminuição no volume de dados de treinamento. Para garantir o mesmo fator de redução de peso para diferentes conjuntos de dados de treinamento, usaremos o parâmetro de regularização λ = 5,0 com um conjunto de treinamento completo e reduza-o proporcionalmente com uma diminuição nos volumes de dados.


Pode-se observar que a precisão da classificação cresce significativamente com o aumento dos dados de treinamento. É provável que esse crescimento continue com um aumento adicional nos volumes. Obviamente, a julgar pelo gráfico acima, estamos nos aproximando da saturação. No entanto, suponha que refizemos este gráfico para uma dependência logarítmica da quantidade de dados de treinamento:


Vê-se que, no final, o gráfico ainda tende a subir. Isso sugere que, se coletarmos uma quantidade muito maior de dados - por exemplo, milhões ou mesmo bilhões de exemplos manuscritos, em vez de 50.000 -, provavelmente obteremos uma rede de trabalho muito melhor, mesmo de tamanho tão pequeno.

Obter mais dados de treinamento é uma ótima idéia. Infelizmente, isso pode ser caro, portanto, na prática, nem sempre é possível. No entanto, há outra idéia que pode funcionar quase tão bem - aumentar artificialmente o conjunto de dados. Por exemplo, suponha que tiremos uma imagem de cinco do MNIST e giremos um pouco, graus por 15:



Esta é claramente a mesma figura. Mas no nível de pixels, é muito diferente das imagens disponíveis no banco de dados MNIST. É razoável supor que a adição dessa imagem ao conjunto de dados de treinamento possa ajudar nossa rede a aprender mais sobre a classificação de imagens. Além disso, obviamente não estamos limitados à capacidade de adicionar apenas uma imagem. Podemos expandir nossos dados de treinamento fazendo algumas pequenas reviravoltas em todas as imagens de treinamento do MNIST e, em seguida, usando o conjunto estendido de dados de treinamento para aumentar a eficiência da rede.

Essa ideia é muito poderosa e é amplamente usada. Vejamos os resultados do trabalho científicoque aplicaram várias variações dessa idéia ao MNIST. Uma das arquiteturas das redes consideradas por eles era semelhante à que usamos - uma rede de distribuição direta com 800 neurônios ocultos, usando a função de custo com entropia cruzada. Ao lançar essa rede com o conjunto de treinamento padrão do MNIST, eles obtiveram uma precisão de classificação de 98,4%. Mas eles expandiram os dados de treinamento, usando não apenas a rotação que descrevi acima, mas também a transferência e distorção de imagens. Depois de treinar a rede em dados avançados, eles aumentaram sua precisão para 98,9%. Eles também experimentaram o chamado "Distorção elástica", um tipo especial de distorção de imagem, projetado para eliminar as vibrações aleatórias dos músculos da mão. Usando distorções elásticas para expandir os dados, eles alcançaram precisão de 99,3%. Em essência, eles expandiram sua experiência de rede,dando-lhe várias variações manuscritas encontradas em caligrafia real.

Variantes dessa idéia podem ser usadas para melhorar o desempenho de muitas tarefas de aprendizado, não apenas para reconhecimento de manuscrito. O princípio geral é expandir os dados de treinamento aplicando operações a eles que refletem as variações encontradas na realidade. Tais variações são fáceis de encontrar. Suponha que estamos criando o NS para reconhecimento de fala. As pessoas podem reconhecer a fala mesmo com distorções, como ruído de fundo. Portanto, você pode expandir os dados adicionando ruído de fundo. Também somos capazes de reconhecer a fala acelerada e lenta. Essa é outra maneira de expandir os dados de treinamento. Essas técnicas nem sempre são usadas - por exemplo, em vez de expandir o conjunto de treinamento adicionando ruído, pode ser mais eficiente limpar a entrada aplicando um filtro de ruído a elas. E, no entanto, vale lembrar a ideia de expandir o conjunto de treinamento,e procure maneiras de usá-lo.

Exercício

• Como discutimos acima, uma maneira de estender os dados de treinamento do MNIST é usar pequenas rotações das imagens de treinamento. Que problema pode surgir se permitirmos a rotação das imagens em qualquer ângulo?

Digressão de big data e o significado da comparação da precisão da classificação

Vamos dar uma olhada novamente em como a precisão do nosso NS varia dependendo do tamanho do conjunto de treinamento:


Suponha que, em vez de usar o NS, usássemos outra tecnologia de aprendizado de máquina para classificar números. Por exemplo, vamos tentar usar o método de máquina de vetores de suporte (SVM), que conhecemos brevemente no capítulo 1. Como então, não se preocupe se você não estiver familiarizado com o SVM, não precisamos entender seus detalhes. Usaremos o SVM através da biblioteca scikit-learn. Veja como a eficácia do SVM varia com o tamanho do conjunto de treinamento. Para comparação, coloquei o cronograma e os resultados da Assembléia Nacional.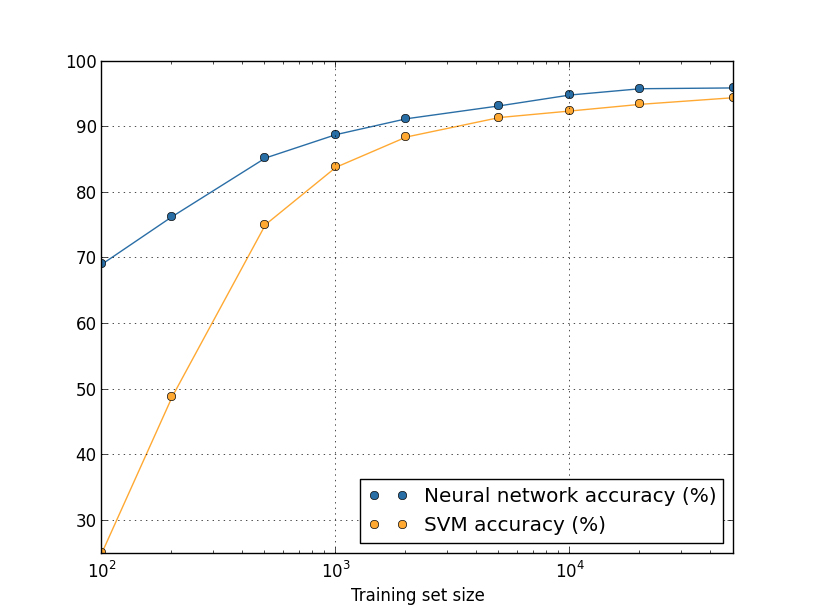


Provavelmente a primeira coisa que chama a sua atenção - o NS supera o SVM em qualquer tamanho do conjunto de treinamento. Isso é bom, embora não valha a pena tirar conclusões de longo alcance disso, pois usei as configurações predefinidas de aprendizado de scikit e trabalhámos bastante seriamente em nosso NS. Um fato menos vívido, mas mais interessante, que segue no gráfico, é que, se treinarmos nosso SVM usando 50.000 imagens, ele funcionará melhor (precisão de 94,48%) do que nosso NS treinado com 5000 imagens ( 93,24%). Em outras palavras, um aumento no volume de dados de treinamento às vezes compensa a diferença nos algoritmos MO.

Algo mais interessante pode acontecer. Suponha que estamos tentando resolver um problema usando dois algoritmos MO, A e B. Às vezes acontece que o algoritmo A está à frente do algoritmo B em um conjunto de dados de treinamento e o algoritmo B está à frente do algoritmo A em outro conjunto de dados de treinamento. Não vimos isso acima - os gráficos se cruzariam - mas isso acontece . A resposta correta para a pergunta: "O algoritmo A é superior ao algoritmo B?" de fato, este: "Que conjunto de dados de treinamento você está usando?"

Tudo isso deve ser levado em consideração, tanto no desenvolvimento quanto na leitura de artigos científicos. Muitos trabalhos concentram-se em encontrar novos truques para extrair melhores resultados em conjuntos de dados de medição padrão. “Nossa tecnologia de superalimentos nos proporcionou uma melhoria de X% no conjunto comparativo padrão Y” - o formulário de inscrição canônico nesse estudo. Às vezes, essas declarações são realmente interessantes, mas vale a pena entender que elas são aplicáveis ​​apenas no contexto de um conjunto de treinamento específico. Imagine uma história alternativa na qual as pessoas que inicialmente criaram um conjunto comparativo receberam uma bolsa de pesquisa maior. Eles poderiam usar dinheiro extra para coletar dados adicionais. É possível que a “melhoria” da tecnologia super-duper desapareça em um conjunto de dados maior. Em outras palavras,a essência da melhoria pode ser apenas um acidente. A partir disso, a seguinte moralidade deve ser levada ao campo da aplicação prática: precisamos de algoritmos aprimorados e dados de treinamento aprimorados. Não há nada de errado em procurar algoritmos aprimorados, mas certifique-se de não se concentrar nisso, ignorando a maneira mais fácil de vencer aumentando o volume ou a qualidade dos dados de treinamento.

Desafio

• . ? . – , , , . , . - ? , .

Sumário

Concluímos nossa imersão em reciclagem e regularização. Obviamente, retornaremos a esses problemas. Como mencionei várias vezes, a reciclagem é um grande problema no campo do NS, especialmente quando os computadores se tornam mais poderosos e podemos treinar redes maiores. Como resultado, há uma necessidade urgente de desenvolver técnicas eficazes de regularização para reduzir a reciclagem, portanto essa área é muito ativa atualmente.

Inicialização de peso

Quando criamos nosso NS, precisamos fazer uma escolha dos valores iniciais de pesos e compensações. Até agora, nós os escolhemos de acordo com as diretrizes descritas brevemente no Capítulo 1. Deixe-me lembrá-lo de que escolhemos pesos e compensações com base em uma distribuição gaussiana independente com uma expectativa matemática de 0 e um desvio padrão de 1. Essa abordagem funcionou bem, mas parece bastante arbitrária, portanto vale a pena. revise-o e pense se é possível encontrar uma maneira melhor de atribuir os pesos e deslocamentos iniciais e, talvez, ajudar nossos NSs a aprender mais rapidamente.

Acontece que o processo de inicialização pode ser seriamente aprimorado em comparação com a distribuição gaussiana normalizada. Para entender isso, digamos que trabalhamos com uma rede com um grande número de neurônios de entrada, digamos, de 1000. E digamos que usamos a distribuição Gaussiana normalizada para inicializar pesos conectados à primeira camada oculta. Até agora, focarei apenas nas escalas que conectam os neurônios de entrada ao primeiro neurônio na camada oculta e ignorarei o restante da rede:


Por simplicidade, vamos imaginar que estamos tentando treinar a rede com a entrada x, na qual metade dos neurônios de entrada está ativada, ou seja, eles têm um valor de 1 e a metade está desativada, ou seja, eles têm um valor de 0. O próximo argumento funciona em um caso mais geral, mas é mais fácil para você vai entendê-lo neste exemplo em particular. Considere a soma ponderada z = w _j w _j x _j + b de entradas para um neurônio oculto. 500 membros da soma desaparecem porque o x _j correspondente é 0. Portanto, z é a soma de 501 variáveis ​​aleatórias Gaussianas normalizadas, 500 pesos e 1 deslocamento adicional. Portanto, o próprio valor z tem uma distribuição gaussiana com uma expectativa matemática de 0 e um desvio padrão de √501 ≈ 22,4. Ou seja, z tem uma distribuição gaussiana bastante ampla, sem picos acentuados:


Em particular, este gráfico mostra que | z | é provavelmente muito grande, ou seja, z ≫ 1 ou z ≫ -1. Nesse caso, a saída dos neurônios ocultos σ (z) será muito próxima de 1 ou 0. Isso significa que nosso neurônio oculto ficará saturado. E quando isso acontece, como já sabemos, pequenas alterações nos pesos produzirão pequenas alterações na ativação de um neurônio oculto. Essas pequenas mudanças, por sua vez, praticamente não afetarão os nêutrons restantes na rede, e veremos as pequenas mudanças correspondentes na função de custo. Como resultado, esses pesos serão treinados muito lentamente quando usarmos o algoritmo de descida de gradiente. Isso é semelhante à tarefa que já discutimos neste capítulo, na qual os neurônios de saída saturados com valores incorretos fazem com que o aprendizado desacelere. Costumávamos resolver esse problema escolhendo inteligentemente uma função de custo. Infelizmente, embora isso tenha ajudado com neurônios de saída saturados, não ajuda em nada com a saturação de neurônios ocultos.

Agora eu falei sobre as escalas de entrada da primeira camada oculta. Naturalmente, os mesmos argumentos se aplicam às seguintes camadas ocultas: se os pesos nas camadas ocultas posteriores forem inicializados usando distribuições Gaussianas normalizadas, sua ativação será frequentemente próxima de 0 ou 1 e o treinamento será muito lento.

Existe uma maneira de escolher as melhores opções de inicialização para pesos e compensações, para não obtermos essa saturação e evitar atrasos na aprendizagem? Suponha que temos um neurônio com o número de pesos recebidos n _pol . Então, precisamos inicializar esses pesos com distribuições gaussianas aleatórias com uma expectativa matemática de 0 e um desvio padrão de 1 / √n _in . Ou seja, comprimimos os gaussianos e reduzimos a probabilidade de saturação do neurônio. Em seguida, escolheremos uma distribuição gaussiana para deslocamentos com uma expectativa matemática de 0 e um desvio padrão de 1, por razões às quais voltarei um pouco mais tarde. Tendo feito essa escolha, descobrimos novamente que z = w _j w _j x _j + b será uma variável aleatória com uma distribuição gaussiana com uma expectativa matemática de 0, mas com um pico muito mais pronunciado do que antes. Suponha, como antes, que 500 entradas são 0 e 500 são 1. Então é fácil mostrar (veja o exercício abaixo) que z tem uma distribuição gaussiana com uma expectativa matemática de 0 e um desvio padrão de √ (3/2) = 1,22 ... Este gráfico tem um pico muito mais nítido, tanto que, mesmo na imagem abaixo, a situação é um pouco subestimada, porque tive que alterar a escala do eixo vertical em comparação com o gráfico anterior:


Esse neurônio será saturado com uma probabilidade muito menor e, consequentemente, será menos provável que ocorra uma desaceleração no aprendizado.

Exercício

• Confirme que o desvio padrão de z = w _j w _j x _j + b do parágrafo anterior é √ (3/2). Considerações a favor disso: a variação da soma das variáveis ​​aleatórias independentes é igual à soma das variações das variáveis ​​aleatórias individuais; a variação é igual ao quadrado do desvio padrão.

Mencionei acima que continuaremos inicializando os deslocamentos, como antes, com base em uma distribuição gaussiana independente com uma expectativa matemática de 0 e um desvio padrão de 1. E isso é normal, porque não aumenta muito a probabilidade de saturação de nossos neurônios. Na verdade, a inicialização de compensações não importa muito se conseguirmos evitar o problema de saturação. Alguns até tentam inicializar todas as compensações para zero e confiam no fato de que a descida do gradiente pode aprender as compensações apropriadas. Mas como a probabilidade de isso afetar algo é pequena, continuaremos usando o mesmo procedimento de inicialização de antes.

Vamos comparar os resultados das abordagens antiga e nova para inicializar pesos usando a tarefa de classificar números do MNIST. Como antes, usaremos 30 neurônios ocultos, um mini-pacote de tamanho 10, um parâmetro de regularização & lambda = 5.0 e uma função de custo com entropia cruzada. Reduziremos gradualmente a velocidade de aprendizado de η = 0,5 para 0,1, pois dessa forma os resultados serão um pouco melhor visíveis nos gráficos. Você pode aprender usando o método de inicialização de peso antigo:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

Você também pode aprender usando a nova abordagem para inicializar pesos. Isso é ainda mais simples, porque, por padrão, a rede2 inicializa os pesos usando uma nova abordagem. Isso significa que podemos omitir a chamada net.large_weight_initializer () anteriormente:

 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

Traçamos (usando o programa weight_initialization.py):


Nos dois casos, é obtida uma precisão de classificação de 96%. A precisão resultante é quase a mesma nos dois casos. Mas a nova técnica de inicialização chega a esse ponto muito, muito mais rapidamente. No final da última era do treinamento, a abordagem antiga para inicializar pesos atinge uma precisão de 87%, e a nova abordagem já se aproxima de 93%. Aparentemente, uma nova abordagem para inicializar pesos começa de uma posição muito melhor, para obter bons resultados muito mais rapidamente. O mesmo fenômeno é observado se construirmos os resultados para uma rede com 100 neurônios:


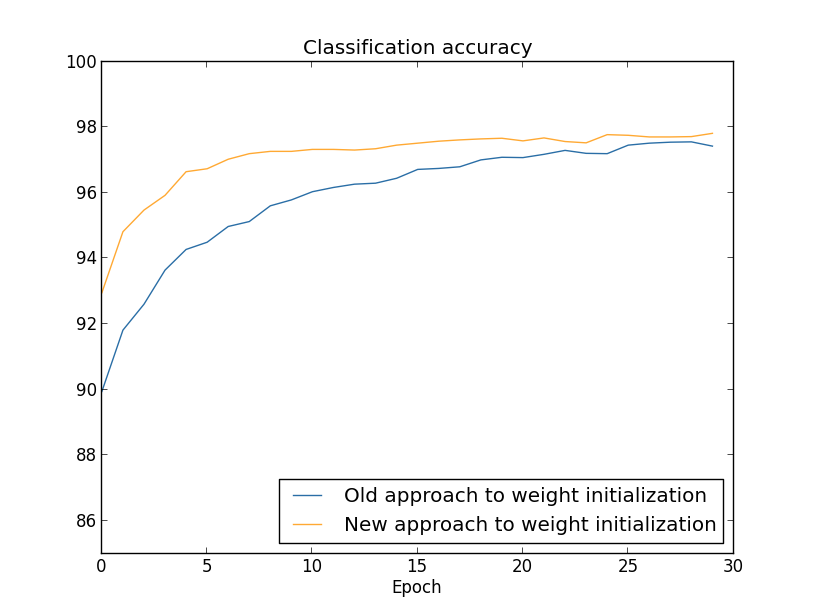
Nesse caso, duas curvas não ocorrem. No entanto, minhas experiências dizem que, se você adicionar um pouco mais de épocas, a precisão começará a quase coincidir. Portanto, com base nessas experiências, podemos dizer que melhorar a inicialização dos pesos acelera apenas o treinamento, mas não altera a eficiência geral da rede. No entanto, no capítulo 4, veremos exemplos de NSs nos quais a eficiência a longo prazo é significativamente aprimorada como resultado da inicialização dos pesos através de 1 / √n _in . Portanto, melhora não apenas a velocidade da aprendizagem, mas às vezes a eficácia resultante.

A abordagem para inicializar pesos por meio de 1 / √n ajuda a melhorar o treinamento de redes neurais. Outras técnicas para inicializar pesos foram propostas, muitas das quais baseadas nesta idéia básica. Não os considerarei aqui, pois 1 / √n funciona bem para nossos propósitos. Se você estiver interessado, recomendo ler a discussão nas páginas 14 e 15 em um artigo de 2012 de Yoshua Benggio.

Desafio

• A combinação de regularização e um método aprimorado de inicialização de peso. Às vezes, a regularização de L2 nos fornece resultados semelhantes a um novo método de inicialização de pesos. Digamos que usamos a abordagem antiga para inicializar pesos. Descreva um argumento heurístico que prove que: (1) se λ não for muito pequeno, nas primeiras épocas do treinamento, o enfraquecimento dos pesos dominará quase completamente; (2) se ηλ ≪ n, os pesos enfraquecerão e ^{-ηλ / m} vezes na época; (3) se λ não for muito grande, o enfraquecimento dos pesos diminuirá quando os pesos diminuirem para cerca de 1 / √n, onde n é o número total de pesos na rede. Prove que essas condições são atendidas nos exemplos para os quais os gráficos são construídos nesta seção.

Retornando ao reconhecimento de manuscrito: código

Vamos implementar as idéias descritas neste capítulo. Vamos desenvolver um novo programa, network2.py, uma versão aprimorada do programa network.py que criamos no capítulo 1. Se você não vê o código há muito tempo, talvez seja necessário analisá-lo rapidamente. Essas são apenas 74 linhas de código e é fácil de entender.

Assim como em network.py, a estrela de network2.py é a classe Network, que usamos para representar nossos NSs. Inicializamos a instância da classe com uma lista de tamanhos das camadas de rede correspondentes e, com a escolha da função de custo, por padrão, será entropia cruzada:

 class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost 

As primeiras duas linhas do método __init__ são iguais a network.py e são entendidas por elas mesmas. As próximas duas linhas são novas e precisamos entender em detalhes o que estão fazendo.

Vamos começar com o método default_weight_initializer. Ele usa uma abordagem nova e aprimorada para inicializar pesos. Como vimos, nessa abordagem, os pesos que entram no neurônio são inicializados com base em uma distribuição gaussiana independente com uma expectativa matemática de 0 e um desvio padrão de 1 dividido pela raiz quadrada do número de links de entrada para o neurônio. Além disso, esse método inicializará as compensações usando a distribuição Gaussiana com uma média de 0 e um desvio padrão de 1. Aqui está o código:

  def default_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] 

Para entender, é necessário lembrar que np é uma biblioteca Numpy que lida com álgebra linear. Nós o importamos no início do programa. Observe também que não inicializamos deslocamentos na primeira camada de neurônios. A primeira camada é de entrada, portanto, as compensações não são usadas. O mesmo foi network.py.

Além do método default_weight_initializer, criaremos um método large_weight_initializer. Inicializa pesos e compensações usando a abordagem antiga do Capítulo 1, onde pesos e compensações são inicializados com base em uma distribuição Gaussiana independente com uma expectativa matemática de 0 e um desvio padrão de 1. Esse código, é claro, não é muito diferente do default_weight_initializer:

  def large_weight_initializer(self): self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] 

Incluí esse método principalmente porque era mais conveniente comparar os resultados deste capítulo e do capítulo 1. Não consigo imaginar opções reais nas quais eu recomendaria usá-lo!

A segunda novidade do método __init__ será a inicialização do atributo cost. Para entender como isso funciona, vejamos a classe que usamos para representar a função de custo entre entropia (a diretiva @staticmethod diz ao intérprete que esse método é independente do objeto, para que o parâmetro self não seja passado para os métodos fn e delta).

 class CrossEntropyCost(object): @staticmethod def fn(a, y): return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): return (ay) 

Vamos descobrir. A primeira coisa que pode ser vista aqui é que, embora a entropia cruzada seja uma função do ponto de vista matemático, nós a implementamos como uma classe python, não como uma função python. Por que eu decidi fazer isso? Em nossa rede, o valor desempenha dois papéis diferentes. Óbvio - é uma medida de quão bem a ativação da saída a corresponde à saída desejada y. Esta função é fornecida pelo método CrossEntropyCost.fn. (A propósito, observe que chamar np.nan_to_num dentro de CrossEntropyCost.fn garante que o Numpy processe corretamente o logaritmo dos números próximos a zero). No entanto, a função de custo é usada em nossa rede da segunda maneira. Recordamos no Capítulo 2 que, ao iniciar o algoritmo de retropropagação, precisamos considerar o erro de saída da rede δ ^L. A forma do erro de saída depende da função de custo: diferentes funções de custo terão diferentes formas de erro de saída. Para entropia cruzada, o erro de saída, como segue na equação (66), será igual a:

$$

$$\ delta ^ L = a ^ L-y \ tag {99}$$

Portanto, defino um segundo método, CrossEntropyCost.delta, cujo objetivo é explicar à rede como calcular o erro de saída. E então combinamos esses dois métodos em uma classe que contém tudo o que nossa rede precisa saber sobre a função de custo.

Por um motivo semelhante, network2.py contém uma classe que representa uma função de custo quadrático. Incluindo isso para comparação com os resultados do Capítulo 1, já que no futuro usaremos principalmente entropia cruzada. O código está abaixo. O método QuadraticCost.fn é um cálculo simples do custo quadrático associado à saída a e à saída desejada y. O valor retornado por QuadraticCost.delta é baseado na expressão (30) para o erro de saída do valor quadrático, que derivamos no capítulo 2.

 class QuadraticCost(object): @staticmethod def fn(a, y): return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): return (ay) * sigmoid_prime(z) 

Agora descobrimos as principais diferenças entre network2.py e network2.py. Tudo é muito simples. Existem outras pequenas mudanças que descreverei abaixo, incluindo a implementação da regularização de L2. Antes disso, vejamos o código completo network2.py. Não é necessário estudá-lo em detalhes, mas vale a pena entender a estrutura básica, em particular, ler os comentários para entender o que cada uma das partes do programa faz. É claro que não proíbo de me aprofundar nessa questão o quanto você quiser! Se você se perder, tente ler o texto após o programa e retorne ao código novamente. Em geral, aqui está:

 """network2.py ~~~~~~~~~~~~~~   network.py,            .   –      , ,   .     ,    .   ,       . """ ####  #  import json import random import sys #  import numpy as np ####   ,      class QuadraticCost(object): @staticmethod def fn(a, y): """ ,    ``a``    ``y``. """ return 0.5*np.linalg.norm(ay)**2 @staticmethod def delta(z, a, y): """  delta   .""" return (ay) * sigmoid_prime(z) class CrossEntropyCost(object): @staticmethod def fn(a, y): """ ,    ``a``    ``y``. np.nan_to_num    .  ,   ``a``  ``y``      1.0,   (1-y)*np.log(1-a)  nan. np.nan_to_num ,       (0.0). """ return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a))) @staticmethod def delta(z, a, y): """  delta   .  ``z``    ,          delta     . """ return (ay) ####   Network class Network(object): def __init__(self, sizes, cost=CrossEntropyCost): """  sizes      .  ,      Network      ,     ,     ,    ,  [2, 3, 1].       ,   ``self.default_weight_initializer`` (.  ). """ self.num_layers = len(sizes) self.sizes = sizes self.default_weight_initializer() self.cost=cost def default_weight_initializer(self): """            0    1,       ,       .          0    1.    ,         ,           . """ self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def large_weight_initializer(self): """          0    1.          0    1.    ,         ,           .         1,    .       . """ self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]] self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])] def feedforward(self, a): """  ,  ``a``  .""" for b, w in zip(self.biases, self.weights): a = sigmoid(np.dot(w, a)+b) return a def SGD(self, training_data, epochs, mini_batch_size, eta, lmbda = 0.0, evaluation_data=None, monitor_evaluation_cost=False, monitor_evaluation_accuracy=False, monitor_training_cost=False, monitor_training_accuracy=False): """     -    . ``training_data`` –   ``(x, y)``,       .       ,    ``lmbda``.    ``evaluation_data``,     ,   .         ,     ,   .      :   ,    ,   ,              .  ,      30 ,        30 ,        .     ,   . """ if evaluation_data: n_data = len(evaluation_data) n = len(training_data) evaluation_cost, evaluation_accuracy = [], [] training_cost, training_accuracy = [], [] for j in xrange(epochs): random.shuffle(training_data) mini_batches = [ training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)] for mini_batch in mini_batches: self.update_mini_batch( mini_batch, eta, lmbda, len(training_data)) print "Epoch %s training complete" % j if monitor_training_cost: cost = self.total_cost(training_data, lmbda) training_cost.append(cost) print "Cost on training data: {}".format(cost) if monitor_training_accuracy: accuracy = self.accuracy(training_data, convert=True) training_accuracy.append(accuracy) print "Accuracy on training data: {} / {}".format( accuracy, n) if monitor_evaluation_cost: cost = self.total_cost(evaluation_data, lmbda, convert=True) evaluation_cost.append(cost) print "Cost on evaluation data: {}".format(cost) if monitor_evaluation_accuracy: accuracy = self.accuracy(evaluation_data) evaluation_accuracy.append(accuracy) print "Accuracy on evaluation data: {} / {}".format( self.accuracy(evaluation_data), n_data) print return evaluation_cost, evaluation_accuracy, \ training_cost, training_accuracy def update_mini_batch(self, mini_batch, eta, lmbda, n): """    ,          -. ``mini_batch`` –    ``(x, y)``, ``eta`` –  , ``lmbda`` -  , ``n`` -     .""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] for x, y in mini_batch: delta_nabla_b, delta_nabla_w = self.backprop(x, y) nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)] nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)] self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)] self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)] def backprop(self, x, y): """  ``(nabla_b, nabla_w)``,      C_x. ``nabla_b``  ``nabla_w`` -    numpy,   ``self.biases`` and ``self.weights``.""" nabla_b = [np.zeros(b.shape) for b in self.biases] nabla_w = [np.zeros(w.shape) for w in self.weights] #   activation = x activations = [x] #      zs = [] #     z- for b, w in zip(self.biases, self.weights): z = np.dot(w, activation)+b zs.append(z) activation = sigmoid(z) activations.append(activation) # backward pass delta = (self.cost).delta(zs[-1], activations[-1], y) nabla_b[-1] = delta nabla_w[-1] = np.dot(delta, activations[-2].transpose()) """  l      ,      . l = 1    , l = 2 – ,   .    ,   python      . """ for l in xrange(2, self.num_layers): z = zs[-l] sp = sigmoid_prime(z) delta = np.dot(self.weights[-l+1].transpose(), delta) * sp nabla_b[-l] = delta nabla_w[-l] = np.dot(delta, activations[-l-1].transpose()) return (nabla_b, nabla_w) def accuracy(self, data, convert=False): """    ``data``,      .   –        .  ``convert``  False,    –    ( )  True,   .    - ,  ``y`` -     .  ,       .           .          ?     –       ,      .   ,      .       mnist_loader.load_data_wrapper. """ if convert: results = [(np.argmax(self.feedforward(x)), np.argmax(y)) for (x, y) in data] else: results = [(np.argmax(self.feedforward(x)), y) for (x, y) in data] return sum(int(x == y) for (x, y) in results) def total_cost(self, data, lmbda, convert=False): """      ``data``.  ``convert``   False,   –  (),   True,   –   . .    ,      ``accuracy``, . """ cost = 0.0 for x, y in data: a = self.feedforward(x) if convert: y = vectorized_result(y) cost += self.cost.fn(a, y)/len(data) cost += 0.5*(lmbda/len(data))*sum( np.linalg.norm(w)**2 for w in self.weights) return cost def save(self, filename): """    ``filename``.""" data = {"sizes": self.sizes, "weights": [w.tolist() for w in self.weights], "biases": [b.tolist() for b in self.biases], "cost": str(self.cost.__name__)} f = open(filename, "w") json.dump(data, f) f.close() ####  Network def load(filename): """    ``filename``.    Network. """ f = open(filename, "r") data = json.load(f) f.close() cost = getattr(sys.modules[__name__], data["cost"]) net = Network(data["sizes"], cost=cost) net.weights = [np.array(w) for w in data["weights"]] net.biases = [np.array(b) for b in data["biases"]] return net ####   def vectorized_result(j): """  10-    1.0   j     .      (0..9)     . """ e = np.zeros((10, 1)) e[j] = 1.0 return e def sigmoid(z): """.""" return 1.0/(1.0+np.exp(-z)) def sigmoid_prime(z): """ .""" return sigmoid(z)*(1-sigmoid(z)) 

Entre as mudanças mais interessantes está a inclusão da regularização de L2. Embora essa seja uma grande mudança conceitual, é tão fácil de implementar que você pode não perceber no código. Na maioria das vezes, isso é simplesmente passar o parâmetro lmbda para diferentes métodos, especialmente o Network.SGD. Todo o trabalho é realizado em uma linha do programa, a quarta do final no método Network.update_mini_batch. Lá, alteramos a regra de atualização da descida do gradiente para incluir a redução de peso. A mudança é pequena, mas afeta seriamente os resultados!

A propósito, isso geralmente acontece ao implementar novas técnicas em redes neurais. Passamos milhares de palavras discutindo a regularização. Conceitualmente, essa é uma coisa bastante sutil e difícil de entender. No entanto, pode ser adicionado trivialmente ao programa! Inesperadamente, técnicas complexas podem ser implementadas com pequenas alterações no código.

Outra alteração pequena, mas importante no código, é a adição de vários sinalizadores opcionais ao método de descida de gradiente estocástico Network.SGD.Esses sinalizadores tornam possível rastrear o custo e a precisão nos dados de treinamento ou nos dados de avaliação, que podem ser transmitidos ao Network.SGD. No início do capítulo, costumamos usar esses sinalizadores, mas deixe-me dar um exemplo de seu uso, apenas como um lembrete:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True) 

Definimos dados de avaliação por meio de dados de validação. No entanto, podemos acompanhar o desempenho em test_data e em qualquer outro conjunto de dados. Também temos quatro sinalizadores que especificam a necessidade de acompanhar o custo e a precisão nos dados de avaliação e nos dados de treinamento. Esses sinalizadores são definidos como Falso por padrão, no entanto, são incluídos aqui para rastrear a eficácia da rede. Além disso, o método Network.SGD de network2.py retorna uma tupla de quatro elementos que representa os resultados do rastreamento. Você pode usá-lo assim:

 >>> evaluation_cost, evaluation_accuracy, ... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5, ... lmbda = 5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True, ... monitor_evaluation_cost=True, ... monitor_training_accuracy=True, ... monitor_training_cost=True) 

Assim, por exemplo, assessment_cost será uma lista de 30 elementos que contêm o custo dos dados estimados no final de cada era. Essas informações são extremamente úteis para entender o comportamento de uma rede neural. Essas informações são extremamente úteis para entender o comportamento da rede. Por exemplo, pode ser usado para desenhar gráficos de aprendizado de rede ao longo do tempo. Foi assim que construí todos os gráficos deste capítulo. No entanto, se um dos sinalizadores não estiver definido, o elemento de tupla correspondente será uma lista vazia.

Outras adições de código incluem o método Network.save, que salva o objeto Rede no disco e a função de carregá-lo na memória. O salvamento e o carregamento são feitos via JSON, não os módulos pickle ou cPickle do Python, que geralmente são usados ​​para salvar no disco e carregar no python. O uso de JSON requer mais código do que seria necessário para pickle ou cPickle. Para entender por que escolhi o JSON, imagine que em algum momento no futuro decidimos mudar nossa classe de rede para que houvesse mais do que neurônios sigmóides. Para implementar essa alteração, provavelmente alteraríamos os atributos definidos no método Network .__ init__. E se apenas usamos pickle para salvar, nossa função de carregamento não funcionaria. O uso de JSON com serialização explícita facilita a garantia deque versões mais antigas do objeto Rede podem ser baixadas.

Existem muitas pequenas alterações no código, mas essas são apenas pequenas variações do network.py. O resultado final é uma extensão do nosso programa de 74 linhas para um programa muito mais funcional de 152 linhas.

Desafio

• Modifique o código abaixo introduzindo a regularização L1 e use-o para classificar os dígitos MNIST por uma rede com 30 neurônios ocultos. Você pode escolher um parâmetro de regularização que permita melhorar o resultado comparado a uma rede sem regularização?
• Network.cost_derivative method network.py. . ? , ? network2.py Network.cost_derivative, CrossEntropyCost.delta. ?