Hoje, veremos um pacote gráfico para a linguagem Julia chamado Luxor . Essa é uma daquelas ferramentas que transformam o processo de criação de imagens vetoriais em solução de problemas lógicos, acompanhada de uma tempestade de emoções.
Cuidado Sob o corte de 8,5 MB de imagens e gifs leves que retratam ovos psicodélicos e objetos quadridimensionais, cuja visualização pode causar leve turvação na mente!
Instalação
https://julialang.org - faça o download da distribuição Julia no site oficial. Em seguida, iniciando o intérprete, direcionamos os comandos para o console:
using Pkg Pkg.add("Colors") Pkg.add("ColorSchemes") Pkg.add("Luxor")
que instalará pacotes para trabalhos avançados com cores e com o próprio Luxor.
Possíveis problemas
O principal problema da programação moderna em geral e do código aberto em particular é que alguns projetos são construídos em cima de outros, herdando todos os erros ou até gerando novos devido a incompatibilidades. Como muitos outros pacotes, o Luxor usa outros pacotes julia para seu trabalho, que, por sua vez, são conchas das soluções existentes.
Portanto, o ImageMagick.jl não queria baixar e salvar arquivos. A solução foi encontrada na página original - descobriu-se que ele não gosta do alfabeto cirílico.
O problema número dois surgiu com o pacote gráfico de baixo nível do Cairo no Windows 7. Vou ocultar a solução aqui:
Dançando com um pandeiro- Digitamos o intérprete
]add Gtk - o pacote para trabalhar com o gui começará a ser instalado e provavelmente cairá durante a construção - Em seguida, baixe gtk + -bundle_3.6.4-20130513_win64
- Durante a instalação, tudo era necessário na pasta com os pacotes de Julia, mas o gtk não foi concluído durante a execução do item, então baixamos a versão final para nossa máquina - jogamos o conteúdo do arquivo baixado no diretório C: \ Users \ User.julia \ packages \ WinRPM \ Y9QdZ \ deps \ usr \ x86_64-w64-mingw32 \ sys-root \ mingw (Seu caminho pode variar)
- Execute julia e dirija
]build Gtk e depois de construir using Gtk e, por uma questão de fidelidade, reconstrua Luxor: ]build Luxor - Reiniciamos julia e podemos usar com segurança tudo o que precisamos:
using Luxor
No caso de outros problemas, tentamos encontrar nosso próprio caso.
Se você quiser experimentar animação
O pacote Luxor cria animações usando o ffmpeg , desde que esteja presente no seu computador. O ffmpeg é uma biblioteca de código aberto de plataforma cruzada para processar arquivos de vídeo e áudio, algo muito útil (há uma boa excursão no hub ). Instale-o:
- Faça o download do ffmpeg offsite. No meu caso, este é um download para Windows
- Descompacte e escreva o caminho para ffmpeg.exe na variável Path .
Mais sobre entupimento no Path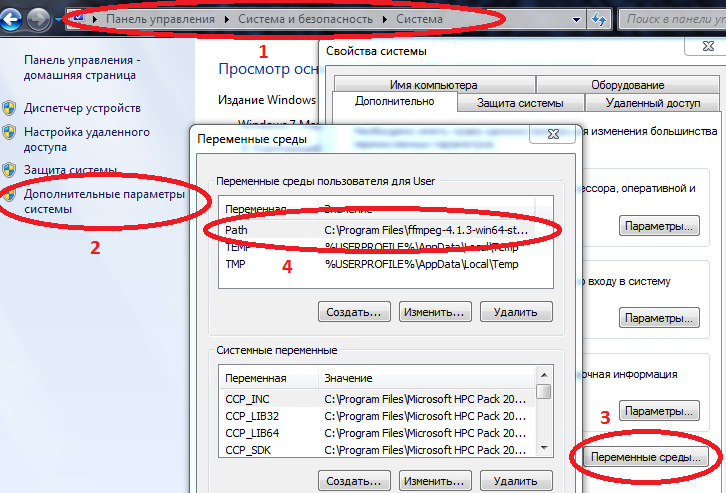
Computador / Propriedades do sistema / Parâmetros avançados do sistema / Variáveis de ambiente / Caminho (Crie se não estiver) e adicione o caminho ao seu ffmpeg.exe
Exemplo C: \ Arquivos de Programas \ ffmpeg-4.1.3-win64-static \ bin
se Path já tiver valores, separe-os com um ponto e vírgula.
Agora, se você conduzir o ffmpeg com os parâmetros necessários no console de comando ( cmd ), ele iniciará e funcionará, e Julia somente se comunicará com ele.
Olá mundo
Vamos começar com uma pequena armadilha - ao criar uma imagem, um arquivo gráfico é criado e salvo no diretório de trabalho. Ou seja, ao trabalhar no REPL, a pasta raiz julia ficará entupida de figuras e, se você desenhar no Jupyter, as figuras serão acumuladas ao lado do bloco de notas do projeto, portanto, será um bom hábito definir o diretório de trabalho em um local separado antes de iniciar o trabalho:
using Luxor cd("C:\\Users\\User\\Desktop\\mycop")
Crie o primeiro desenho
Drawing(220, 220, "hw.png") origin() background("white") sethue("black") text("Hello world") circle(Point(0, 0), 100, :stroke) finish() preview()

Drawing() cria um desenho, por padrão no formato PNG, o nome do arquivo padrão é 'luxor-drawing.png', o tamanho padrão é 800x800, para todos os formatos, exceto png, você pode especificar tamanhos não inteiros e também tamanhos de papel ("A0 "," A1 "," A2 "," A3 "," A4 "...)
finish() - termina o desenho e fecha o arquivo. Você pode abri-lo em um aplicativo de visualização externa usando preview() , que ao trabalhar no Jupyter (IJulia) exibirá um arquivo PNG ou SVG no bloco de notas. Ao trabalhar no Juno, ele exibirá um arquivo PNG ou SVG no painel Gráfico. Em Repl, é chamada a ferramenta para trabalhar com imagens definidas para este formato no seu sistema operacional.
O mesmo pode ser escrito em formato abreviado usando macros
@png begin text("Hello world") circle(Point(0, 0), 100, :stroke) end
Para formatos vetoriais EPS, SVG, PDF, tudo funciona da mesma maneira.
Ovo euclidiano

Esta é uma maneira bastante interessante de desenhar um ovo, e se você conectar os pontos-chave e cortar ao longo das linhas recebidas, um excelente tangram sairá
Vamos começar com o círculo:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) end 200 200 "egg0"

Tudo é extremamente simples: setdash("dot") - desenhe com pontos, sethue("gray30") - cor da linha: quanto menor, mais escuro, mais perto de 100, mais branco. A classe de pontos é definida sem nós e o centro de coordenadas (0,0) pode ser especificado pela letra O Adicione dois círculos e assine os pontos:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke) end 600 400 "egg2"
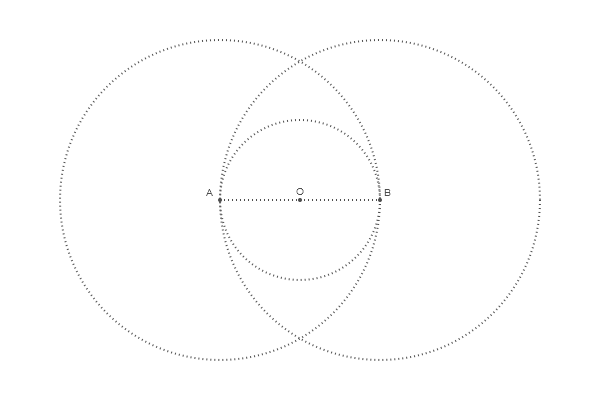
Para procurar pontos de interseção, existe uma função chamada intersectionlinecircle() que localiza o ponto ou pontos onde a linha cruza o círculo. Assim, podemos encontrar dois pontos em que um dos círculos cruza uma linha vertical imaginária traçada através de O. Devido à simetria, podemos processar apenas o círculo A.
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
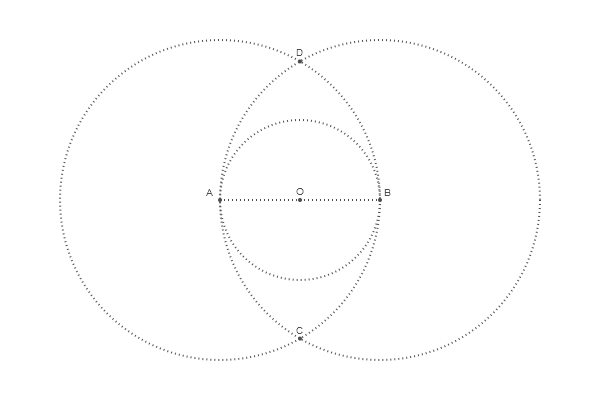
Para determinar o centro do círculo superior, encontramos a interseção OD
Código @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

O raio do círculo subordinado é determinado pela restrição a dois círculos grandes:
Código @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

O ovo está pronto! Resta montá-lo a partir de quatro arcos especificados pela função arc2r() e preencher a área:
Código @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
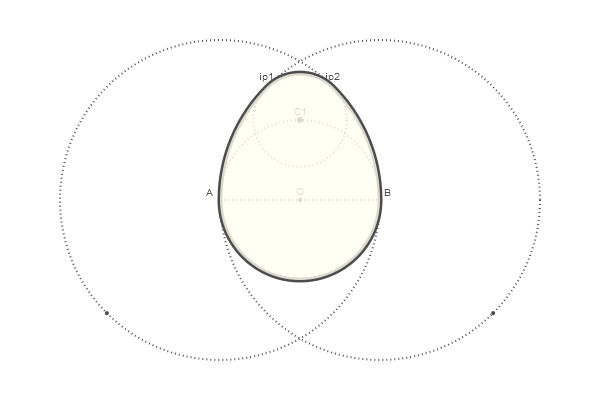
E agora, para nos entregarmos adequadamente, levaremos nossas realizações a
a função function egg(radius, action=:none) A, B = [Point(x, 0) for x in [-radius, radius]] nints, C, D = intersectionlinecircle(Point(0, -2radius), Point(0, 2radius), A, 2radius) flag, C1 = intersectionlinecircle(C, D, O, radius) nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius) nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius) if distance(C1, I1) < distance(C1, I2) ip1 = I1 else ip1 = I2 end if distance(C1, I3) < distance(C1, I4) ip2 = I3 else ip2 = I4 end newpath() arc2r(B, A, ip1, :path) arc2r(C1, ip1, ip2, :path) arc2r(A, ip2, B, :path) arc2r(O, B, A, :path) closepath() do_action(action) end
Usamos cores aleatórias, pintura de camadas e várias condições iniciais:
@png begin setopacity(0.7) for θ in range(0, step=π/6, length=12) @layer begin rotate(θ) translate(100, 50)


Além do traçado e preenchimento, você pode usar o contorno como uma área de recorte (cortar outra imagem na forma de um ovo) ou como base para vários designers. A função egg () cria um esboço e permite aplicar uma ação a ele. Também é possível transformar nossa criação em um polígono (uma matriz de pontos). O código a seguir converte o contorno de um ovo em um polígono e depois move o outro ponto do polígono até a metade do centróide.
@png begin egg(160, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) circle(pc, 5, :fill) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.5) end poly(pgon, :stroke) end 350 500 "polyegg"

A aparência desigual dos pontos internos aqui aparece como resultado das configurações de conexão de linha padrão. Experimente setlinejoin("round") para ver se isso altera a geometria. Bem, agora vamos tentar offsetpoly() criando um contorno poligonal fora ou dentro de um polígono existente.
@png begin egg(80, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.9) end for i in 30:-3:-8 randomhue() op = offsetpoly(pgon, i) poly(op, :stroke, close=true) end end 350 500 "polyeggs"

Pequenas mudanças na regularidade dos pontos criados pela conversão do caminho em um polígono e no número diferente de amostras que ele produziu são constantemente amplificadas em contornos sucessivos.
Animação
Primeiro, vamos definir as funções que implementam o plano de fundo e a renderização do ovo, dependendo do número do quadro:
Código using Colors demo = Movie(400, 400, "test") function backdrop(scene, framenumber) background("black") end function frame(scene, framenumber) setopacity(0.7) θ = framenumber * π/6 @layer begin rotate(θ) translate(100, 50) egg(50, :path) setline(10) randomhue() fillpreserve() randomhue() strokepath() end end
A animação é implementada por um conjunto simples de comandos:
animate(demo, [ Scene(demo, backdrop, 0:12), Scene(demo, frame, 0:12, easingfunction=easeinoutcubic, optarg="made with Julia") ], framerate=10, tempdirectory="C:\\Users\\User\\Desktop\\mycop", creategif=true)
O que realmente causa nosso ffmpeg
run(`ffmpeg -f image2 -i $(tempdirectory)/%10d.png -vf palettegen -y $(seq.stitle)-palette.png`) run(`ffmpeg -framerate 30 -f image2 -i $(tempdirectory)/%10d.png -i $(seq.stitle)-palette.png -lavfi paletteuse -y /tmp/$(seq.stitle).gif`)
Ou seja, uma série de imagens é criada e, em seguida, um GIF é montado a partir desses quadros:

Pentahore
Ele é um cinco - core - o simplex quadridimensional correto. Para desenhar e manipular objetos quadridimensionais em imagens bidimensionais, primeiro definimos
classe ponto tridimensional struct Point4D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 w::Float64 end Point4D(a::Array{Float64, 1}) = Point4D(a...) Base.size(pt::Point4D) = (4, ) Base.getindex(pt::Point4D, i) = [pt.x, pt.y, pt.z, pt.w][i] struct Point3D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 end Base.size(pt::Point3D) = (3, )
Em vez de definir muitas operações manualmente, podemos definir nossa estrutura como um subtipo de AbstractArray ( mais sobre classes como interfaces )
A principal tarefa que devemos resolver é como converter um ponto 4D em um ponto 2D. Vamos começar com uma tarefa mais simples: como converter um ponto 3D em um ponto 2D, ou seja, Como podemos desenhar uma figura 3D em uma superfície plana? Considere um cubo simples. As superfícies frontal e traseira podem ter as mesmas coordenadas X e Y e variar apenas em seus valores Z.
Código @png begin fontface("Menlo") fontsize(8) setblend(blend( boxtopcenter(BoundingBox()), boxmiddlecenter(BoundingBox()), "skyblue", "white")) box(boxtopleft(BoundingBox()), boxmiddleright(BoundingBox()), :fill) setblend(blend( boxmiddlecenter(BoundingBox()), boxbottomcenter(BoundingBox()), "grey95", "grey45" )) box(boxmiddleleft(BoundingBox()), boxbottomright(BoundingBox()), :fill) sethue("black") setline(2) bx1 = box(O, 250, 250, vertices=true) poly(bx1, :stroke, close=true) label.(["-1 1 1", "-1 -1 1", "1 -1 1", "1 1 1"], slope.(O, bx1), bx1) setline(1) bx2 = box(O, 150, 150, vertices=true) poly(bx2, :stroke, close=true) label.(["-1 1 0", "-1 -1 0", "1 -1 0", "1 1 0"], slope.(O, bx2), bx2, offset=-45) map((x, y) -> line(x, y, :stroke), bx1, bx2) end 400 400 "cube.png"

Portanto, a idéia é projetar um cubo de 3D para 2D, salvando os dois primeiros valores e multiplicando ou alterando-os pelo terceiro valor. Verifique
como isso funciona const K = 4.0 function convert(Point, pt3::Point3D) k = 1/(K - pt3.z) return Point(pt3.x * k, pt3.y * k) end @png begin cube = Point3D[ Point3D(-1, -1, 1), Point3D(-1, 1, 1), Point3D( 1, -1, 1), Point3D( 1, 1, 1), Point3D(-1, -1, -1), Point3D(-1, 1, -1), Point3D( 1, -1, -1), Point3D( 1, 1, -1), ] circle.(convert.(Point, cube) * 300, 5, :fill) end 220 220 "points"

Usando o mesmo princípio, vamos criar um método para converter pontos 4D e uma função que pega uma lista de pontos quadridimensionais e os mapeia duas vezes para uma lista de pontos bidimensionais adequados para o desenho.
function convert(Point3D, pt4::Point4D) k = 1/(K - pt4.w) return Point3D(pt4.x * k, pt4.y * k, pt4.z * k) end function flatten(shape4) return map(pt3 -> convert(Point, pt3), map(pt4 -> convert(Point3D, pt4), shape4)) end
Em seguida, defina os vértices e as faces e verifique como ele funciona em cores
Tyk! const n = -1/√5 const pentachoron = [Point4D(vertex...) for vertex in [ [ 1.0, 1.0, 1.0, n], [ 1.0, -1.0, -1.0, n], [-1.0, 1.0, -1.0, n], [-1.0, -1.0, 1.0, n], [ 0.0, 0.0, 0.0, n + √5]]]; const pentachoronfaces = [ [1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]; @png begin setopacity(0.2) pentachoron2D = flatten(pentachoron) for (n, face) in enumerate(pentachoronfaces) randomhue() poly(1500 * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end 300 250 "5ceil"

Todo desenvolvedor de jogos que se preze deve conhecer os Fundamentos Matemáticos da Máquina Gráfica . Se você nunca tentou compactar, girar, refletir bules no OpenGL - não se assuste, tudo é bem simples. Para refletir um ponto em relação a uma linha reta ou girar um plano em torno de um determinado eixo, é necessário multiplicar as coordenadas por uma matriz especial. Na verdade, determinaremos as matrizes de transformação de que precisamos:
pegar mais function XY(θ) [cos(θ) -sin(θ) 0 0; sin(θ) cos(θ) 0 0; 0 0 1 0; 0 0 0 1] end function XW(θ) [cos(θ) 0 0 -sin(θ); 0 1 0 0; 0 0 1 0; sin(θ) 0 0 cos(θ)] end function XZ(θ) [cos(θ) 0 -sin(θ) 0; 0 1 0 0; sin(θ) 0 cos(θ) 0; 0 0 0 1] end function YZ(θ) [1 0 0 0; 0 cos(θ) -sin(θ) 0; 0 sin(θ) cos(θ) 0; 0 0 0 1] end function YW(θ) [1 0 0 0; 0 cos(θ) 0 -sin(θ); 0 0 1 0; 0 sin(θ) 0 cos(θ)] end function ZW(θ) [1 0 0 0; 0 1 0 0; 0 0 cos(θ) -sin(θ); 0 0 sin(θ) cos(θ)]; end function rotate4(A, matrixfunction) return map(A) do pt4 Point4D(matrixfunction * pt4) end end
Normalmente, você gira pontos em um plano em relação a um objeto unidimensional. Os pontos 3D estão em torno de uma linha 2D (geralmente esse é um dos eixos XYZ). Assim, é lógico que os pontos 4D giram em relação ao plano 3D. Identificamos matrizes que realizam rotação quadridimensional em torno de um plano definido por dois eixos X, Y, Z e W. O plano XY é geralmente o plano da superfície de desenho. Se você perceber o plano XY como uma tela de computador, o plano XZ será paralelo à sua mesa ou piso, e o plano YZ será a parede ao lado da sua mesa, à direita ou à esquerda. Mas e XW, YW e ZW? Esse é o mistério das figuras quadridimensionais: não podemos ver esses planos, apenas podemos imaginar sua existência observando como as formas se movem através deles e ao seu redor.
Agora, definimos as funções para os quadros e costuramos a animação:
spoiler using ColorSchemes function frame(scene, framenumber, scalefactor=1000) background("white")

Bem, e outro ângulo:
Código function frame(scene, framenumber, scalefactor=1000) background("antiquewhite") setlinejoin("bevel") setline(1.0) setopacity(0.2) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) pentachoron2D = flatten( rotate4( pentachoron, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(pentachoronfaces) sethue(get(ColorSchemes.diverging_rainbow_bgymr_45_85_c67_n256, n/length(pentachoronfaces))) poly(scalefactor * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end makemovie(500, 500, "pentachoron-xz-yw.gif", scalefactor=2000)
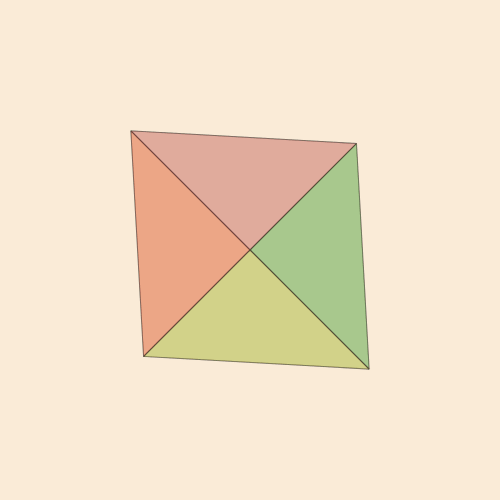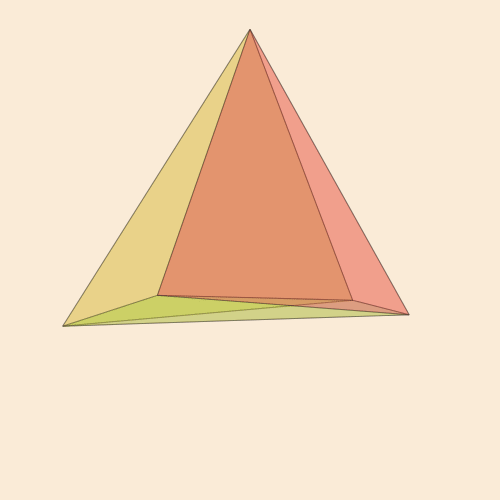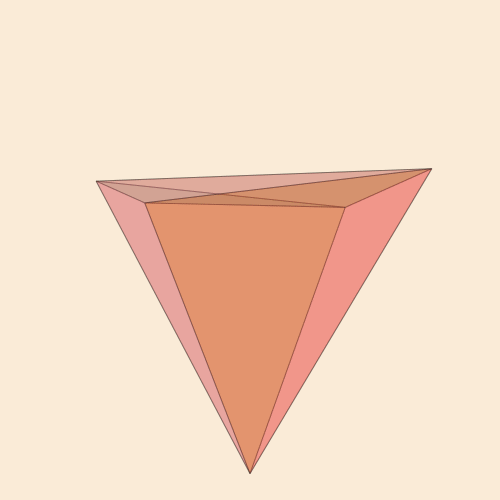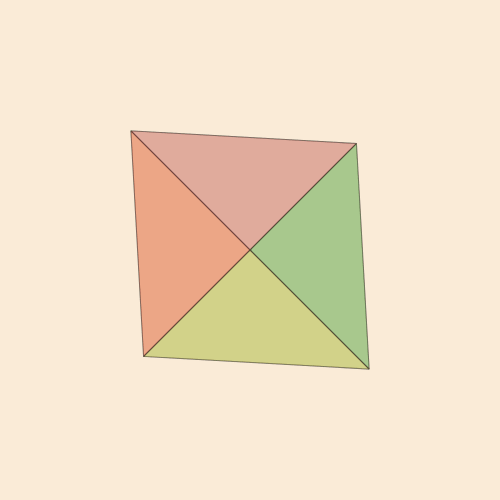
O desejo de realizar um objeto quadridimensional mais popular, o Tesseract, é feito completamente
Tops e Faces const tesseract = [Point4D(vertex...) for vertex in [ [-1, -1, -1, 1], [ 1, -1, -1, 1], [ 1, 1, -1, 1], [-1, 1, -1, 1], [-1, -1, 1, 1], [ 1, -1, 1, 1], [ 1, 1, 1, 1], [-1, 1, 1, 1], [-1, -1, -1, -1], [ 1, -1, -1, -1], [ 1, 1, -1, -1], [-1, 1, -1, -1], [-1, -1, 1, -1], [ 1, -1, 1, -1], [ 1, 1, 1, -1], [-1, 1, 1, -1]]] const tesseractfaces = [ [1, 2, 3, 4], [1, 2, 10, 9], [1, 4, 8, 5], [1, 5, 6, 2], [1, 9, 12, 4], [2, 3, 11, 10], [2, 3, 7, 6], [3, 4, 8, 7], [5, 6, 14, 13], [5, 6, 7, 8], [5, 8, 16, 13], [6, 7, 15, 14], [7, 8, 16, 15], [9, 10, 11, 12], [9, 10, 14, 13], [9, 13, 16, 12], [10, 11, 15, 14], [13, 14, 15, 16]];
Criar animação function frame(scene, framenumber, scalefactor=1000) background("black") setlinejoin("bevel") setline(10.0) setopacity(0.7) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) tesseract2D = flatten( rotate4( tesseract, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(tesseractfaces) sethue([Luxor.lighter_blue, Luxor.lighter_green, Luxor.lighter_purple, Luxor.lighter_red][mod1(n, 4)]...) poly(scalefactor * tesseract2D[face], :fillpreserve, close=true) sethue([Luxor.darker_blue, Luxor.darker_green, Luxor.darker_purple, Luxor.darker_red][mod1(n, 4)]...) strokepath() end end makemovie(500, 500, "tesseract-xz-yw.gif", scalefactor=1000)

Lição de casa: automatize a criação de matrizes de coordenadas e números de vértices ( permutações com repetições e sem repetições, respectivamente ). Além disso, não usamos todas as matrizes de tradução; Cada nova perspectiva traz um novo “Uau!”, Mas decidi não sobrecarregar a página. Bem, você pode experimentar muitas faces e dimensões.
Referências
- Luxor - página de github
- Docs Luxor - um guia com exemplos
- Cairo - uma biblioteca de gráficos de baixo nível; usado pela Luxor como ambiente
- O blog do autor da biblioteca - há muita calma e exemplos mais avançados, incluindo figuras quadridimensionais.