Foto tirada da publicação1. Introdução
Uma das tarefas mais prementes do processamento de sinal digital é a tarefa de limpar o sinal do ruído. Qualquer sinal prático contém não apenas informações úteis, mas também traços de alguns efeitos estranhos de interferência ou ruído. Além disso, durante o diagnóstico de vibração, os sinais dos sensores de vibração possuem um espectro de frequência não estacionário, o que complica a tarefa de filtragem.
Existem muitas maneiras diferentes de remover o ruído de alta frequência de um sinal. Por exemplo, a biblioteca Scipy contém filtros baseados em vários métodos de filtragem: Kalman; suavizando o sinal calculando a média ao longo do eixo do tempo e outros.
No entanto, a vantagem do método de transformada de wavelet discreta (DWT) é a variedade de formas de wavelet. Você pode selecionar uma wavelet, que terá uma forma característica dos fenômenos esperados. Por exemplo, você pode selecionar um sinal em uma determinada faixa de frequência, cuja forma é responsável pela aparência de um defeito.
O objetivo desta publicação é analisar métodos de filtragem de sinais de sensores de vibração usando conversão de sinal DWT, filtro Kalman e o método da média móvel.
Dados de origem para análise
Na publicação, a operação de filtros com base em vários métodos de filtragem será analisada usando
um conjunto de dados da NASA . Dados obtidos na plataforma experimental PRONOSTIA:

O kit contém dados sobre os sinais do sensor de vibração para desgaste de vários tipos de rolamentos. A finalidade das pastas com os arquivos de sinal é apresentada na
tabela :
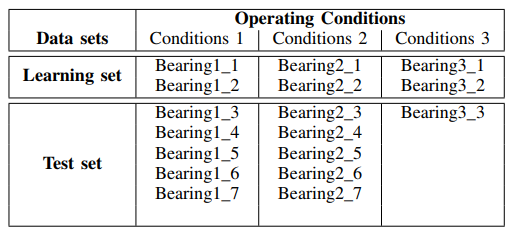
O monitoramento da condição dos rolamentos é fornecido pelos sinais dos sensores de vibração (acelerômetros horizontais e verticais), força e temperatura.

Sinais recebidos para três cargas diferentes:
- Primeiras condições de trabalho: 1800 rpm e 4000 N;
- Segunda condição de trabalho: 1650 rpm e 4200 N;
- Terceiras condições de operação: 1500 rpm e 5000 N.
Para essas condições, usando a conversão contínua de sinal de wavelet, construímos os
escalogramas de potência espectro para os dados do conjunto de testes - um arquivo (para um tipo de rolamento) das pastas: ['Test_set / Bearing1_3 / acc_00001.csv', 'Test_set / Bearing2_3 / acc_00001. csv ',' Test_set / Bearing3_3 / acc_00001.csv '] (consulte a tabela 1).
Listagem do Scaleogramimport scaleogram as scg import pandas as pd from pylab import * import pywt filename_n = ['Test_set/Bearing1_3/acc_00001.csv', 'Test_set/Bearing2_3/acc_00001.csv', 'Test_set/Bearing3_3/acc_00001.csv'] for filename in filename_n: df = pd.read_csv(filename, header=None) signal = df[4].values wavelet = 'cmor1-0.5' ax = scg.cws(signal, scales=arange(1, 40), wavelet=wavelet, figsize=(8, 4), cmap="jet", cbar=None, ylabel=' ', xlabel=" ", yscale="log", title='- %s \n( )'%filename) show()


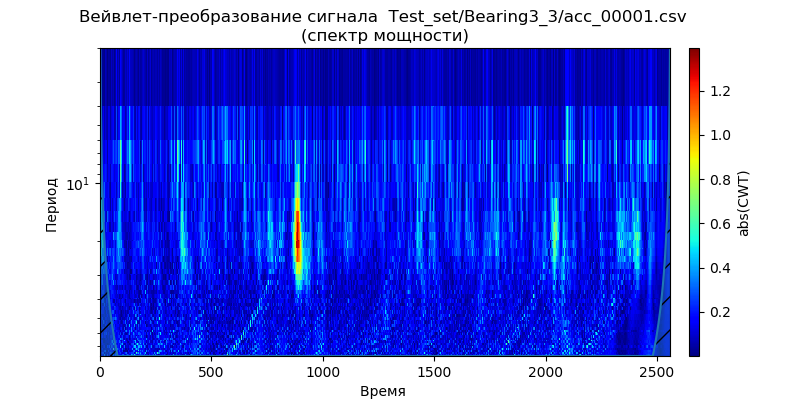
Segue-se dos escalogramas fornecidos que os momentos de aumento da potência do espectro aparecem mais cedo no tempo e demonstram a frequência das condições de operação: 1650 rpm e 4200 N, o que indica degradação acelerada dos mancais nessa faixa de frequência pela força reduzida. Usaremos esse sinal ('Test_set / Bearing2_3 / acc_00001.csv') para analisar os métodos de remoção de ruído.
Desconstrução de sinais usando DWT
Na
publicação, vimos como um banco de filtros é implementado no DWT que pode desconstruir um sinal em suas sub-bandas de frequência. Os coeficientes de aproximação (cA) representam a parte de baixa frequência do sinal (filtro de média). Os coeficientes de detalhe (cD) representam a porção de alta frequência do sinal. A seguir, examinaremos como o DWT pode ser usado para desconstruir um sinal em suas sub-bandas de frequência e restaurar o sinal original.
Existem duas maneiras de resolver o problema de desconstrução de sinal usando as ferramentas PyWavelets:
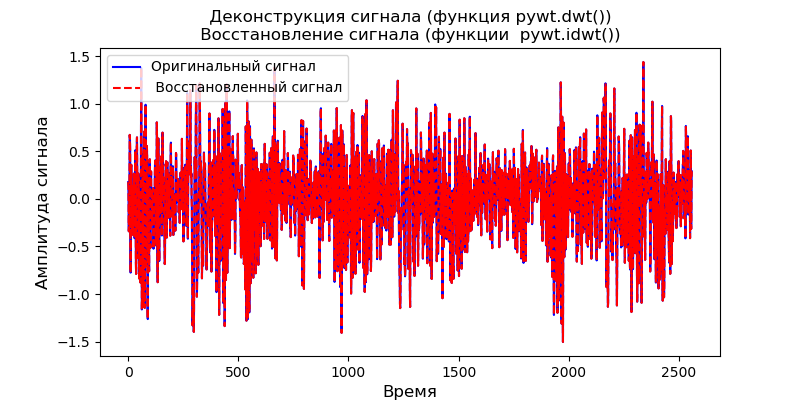
A primeira maneira é aplicar pywt.dwt () ao sinal para extrair os coeficientes de aproximação e detalhe (cA1, cD1). Então, para restaurar o sinal, usaremos pywt.idwt ():
Listagem import pywt from scipy import * import pandas as pd from pylab import * filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values (cA1, cD1) = pywt .dwt (signal, 'db2', 'smooth') r_signal = pywt.idwt (cA1, cD1, 'db2', 'smooth') fig, ax =subplots(figsize=(8,4)) ax.plot(signal, 'b',label=' ') ax.plot(r_signal, 'r', label=' ', linestyle='--') ax.legend(loc='upper left') ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) ax.set_title(' ( pywt.dwt()) \n ( pywt.idwt()) ') show()
A segunda maneira de aplicar a função pywt.wavedec () ao sinal é restaurar todos os coeficientes de aproximação e detalhe para um determinado nível. Esta função recebe o sinal e o nível de entrada como entrada e retorna um conjunto de coeficientes de aproximação (n-ésimo nível) e n conjuntos de coeficientes de detalhes (de 1 a n-ésimo nível). Para desconstrução, aplique pywt.waverec ():
Listagem import pywt import pandas as pd from pylab import * filename = 'Test_set/Bearing3_3/acc_00026.csv' df = pd.read_csv(filename, header=None) signal = df[4].values coeffs = pywt.wavedec(signal, 'db2', level=8) r_signal = pywt.waverec(coeffs, 'db2') fig, ax = plt.subplots(figsize=(8,4)) ax.plot(signal, 'b',label=' ') ax.plot(r_signal, 'r ',label= ' ', linestyle='--') ax.legend(loc='upper left') ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) ax.set_title(' - level.\n ( pywt.wavedec()) ') show()

A segunda maneira de desconstruir e restaurar o sinal é mais conveniente, pois permite definir imediatamente o nível desejado de desconstrução.
Remoção de ruído de alta frequência, eliminando alguns dos coeficientes de detalhes durante a desconstrução do sinal
Restauraremos o sinal excluindo alguns dos coeficientes de detalhes. Como os coeficientes de detalhe representam a parte de alta frequência do sinal, simplesmente filtramos essa parte do espectro de frequências. Se houver ruído de alta frequência no sinal, essa é uma maneira de filtrá-lo.
Na biblioteca PyWavelets, isso pode ser feito usando a função de processamento de limite pywt.threshol ():
pywt.threshold (dados, valor, modo = 'soft', substituto = 0) ¶
data: array_like
Dados numéricos.valor: escalar
Valor limite.mode: {'suave', 'rígido', 'garrote', 'maior', 'menos'}
Define o tipo de limite que será aplicado à entrada. O padrão é 'soft'.substituto: flutuador, opcional
Valor da substituição (padrão: 0).saída: matriz
Matriz de limite.A aplicação da função de processamento de limite para um determinado valor de limite é melhor considerada usando o seguinte exemplo:
>>>> from scipy import* >>> import pywt >>> data =linspace(1, 4, 7) >>> data array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'soft') array([0. , 0. , 0. , 0.5, 1. , 1.5, 2. ]) >>> pywt.threshold(data, 2, 'hard') array([0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'garrote') array([0. , 0. , 0., 0.9,1.66666667, 2.35714286, 3.])
Plotamos o gráfico da função de limite usando a seguinte listagem:
Listagem from scipy import* from pylab import* import pywt s = linspace(-4, 4, 1000) s_soft = pywt.threshold(s, value=0.5, mode='soft') s_hard = pywt.threshold(s, value=0.5, mode='hard') s_garrote = pywt.threshold(s, value=0.5, mode='garrote') figsize=(10, 4) plot(s, s_soft) plot(s, s_hard) plot(s, s_garrote) legend(['soft (0.5)', 'hard (0.5)', 'non-neg. garrote (0.5)']) xlabel(' ') ylabel(' ') show()
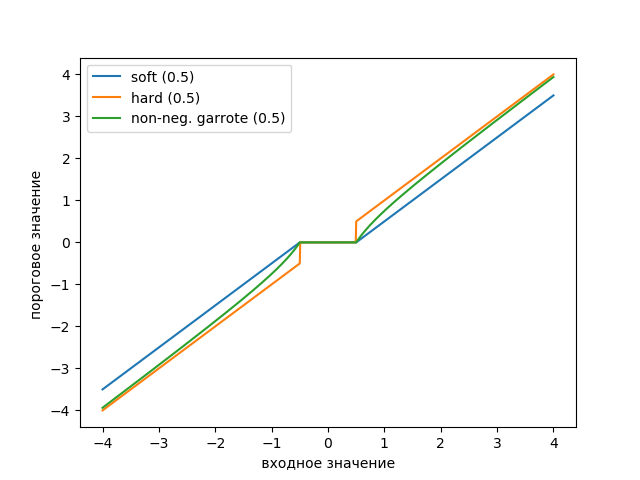
O gráfico mostra que o limiar de Garott não negativo é intermediário entre o limiar suave e rígido. É necessário um par de limites que definam a largura da região de transição.
A influência da função de limiar nas características do filtro
Como se segue no gráfico acima, apenas duas funções de limite 'soft' e 'garrote' são adequadas para que, para estudar sua influência nas características do filtro, anotemos a listagem:
Listagem import pandas as pd from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values v='bior4.4' thres=['soft' ,'garrote'] for w in thres: def lowpassfilter(signal, thresh, wavelet=v): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode=w ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'r', label='DWT ', linewidth=2) ax.legend() ax.set_title(' :%s\n :%s'%(v,w), fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()

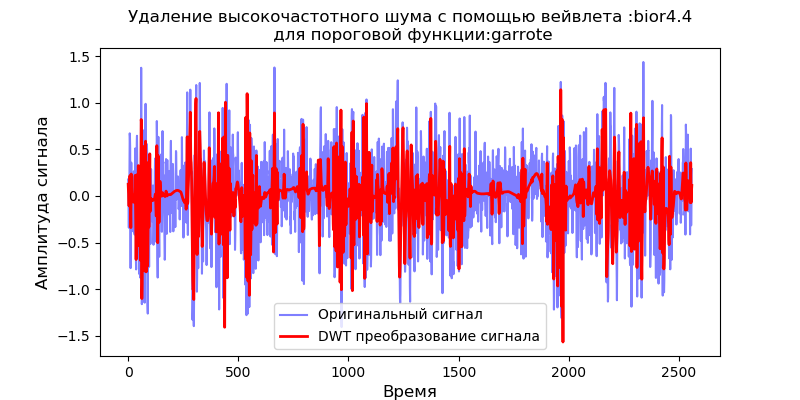
Como se segue nos gráficos, a função soft oferece melhor suavização do que a função 'garrote', portanto, usaremos a função soft no futuro.
A influência do limiar de detalhes nas características do filtro
Para o tipo de filtro em consideração, o limiar para alterar os coeficientes de detalhes é uma característica importante; portanto, estudamos seu efeito usando a seguinte listagem:
Listagem import pandas as pd from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values v='bior4.4' thres=[0.1,0.4,0.6] for w in thres: def lowpassfilter(signal, thresh, wavelet=v): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal,w) ax.plot(rec, 'r', label='DWT ', linewidth=2) ax.legend() ax.set_title(' :%s\n %s'%(v,w), fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()



Como segue nos gráficos obtidos, o limite do nível de detalhe afeta a escala das partes rastreadas. Com um aumento no limiar, a wavelet subtrai o ruído de um nível cada vez maior até que ocorra um aumento excessivo da escala de detalhes e a transformação começa a distorcer a forma do sinal original.Para o nosso sinal, o limiar não deve ser maior que 0,63.
O efeito da wavelet nas características do filtro
A biblioteca PyWavelets possui um número suficiente de wavelets para conversão de DWT, que podem ser obtidas assim:
>>> import pywt >>> print(pywt.wavelist(kind= 'discrete')) ['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20']
A influência da wavelet na característica do filtro depende de sua função primitiva. Para demonstrar essa dependência, selecionamos duas wavelets da família Dobeshi - db1 e db38, e consideramos as seguintes famílias:
Listagem import pywt from pylab import* db_wavelets = ['db1', 'db38'] fig, axarr = subplots(ncols=2, nrows=5, figsize=(14,8)) fig.suptitle(' : db1,db38', fontsize=14) for col_no, waveletname in enumerate(db_wavelets): wavelet = pywt.Wavelet(waveletname) no_moments = wavelet.vanishing_moments_psi family_name = wavelet.family_name for row_no, level in enumerate(range(1,6)): wavelet_function, scaling_function, x_values = wavelet.wavefun(level = level) axarr[row_no, col_no].set_title("{} : {}. : {}. :: {} ".format( waveletname, level, no_moments, len(x_values)), loc='left') axarr[row_no, col_no].plot(x_values, wavelet_function, 'b--') axarr[row_no, col_no].set_yticks([]) axarr[row_no, col_no].set_yticklabels([]) tight_layout() subplots_adjust(top=0.9) show()
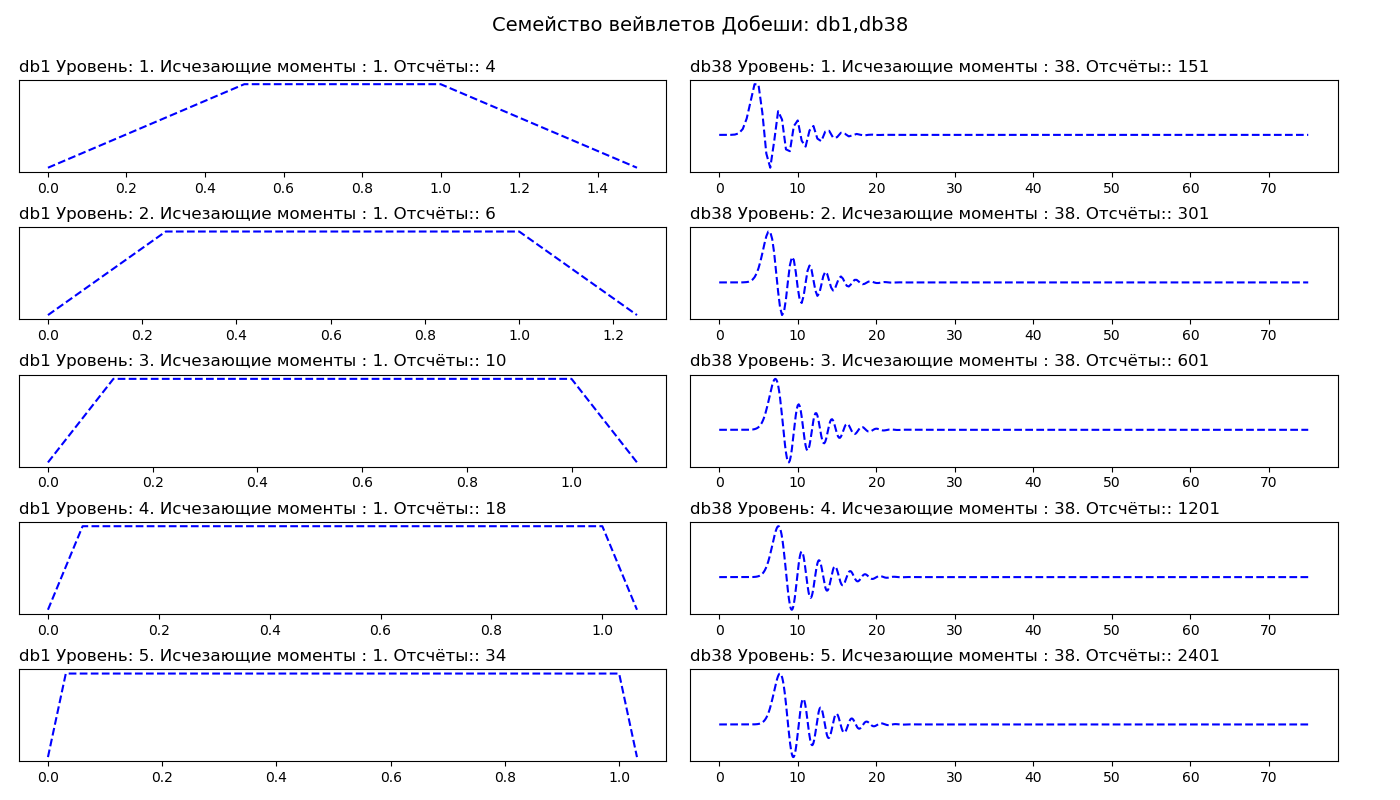
Na primeira coluna, vemos wavelets de Daubeshi de primeira ordem (db1), na segunda coluna da trigésima oitava ordem (db38). Assim, o db1 tem um momento de extinção e o db38 tem 38 momentos de extinção. O número de momentos de desaparecimento está relacionado à ordem de aproximação e à suavidade da wavelet. Se uma wavelet tem P pontos de desaparecimento, ela pode se aproximar de polinômios de grau P - 1.
Wavelets mais suaves criam uma aproximação de sinal mais suave e vice-versa - as wavelets "curtas" rastreiam melhor os picos da função aproximada. Ao escolher uma wavelet, também podemos indicar qual deve ser o nível de decomposição. Por padrão, o PyWavelets seleciona o nível máximo de decomposição possível para o sinal de entrada. O nível máximo de decomposição depende do comprimento do sinal de entrada e da wavelet:
Listagem import pandas as pd import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) data = df[4].values w=['db1', 'db38'] for v in w: n_level=pywt.dwt_max_level(len(data),v) print(' %s : %s ' %(v,n_level))
Para wavelet db1, nível máximo de decomposição: 11
Para wavelet db38, nível máximo de decomposição: 5
Para os valores obtidos dos níveis máximos de decomposição de wavelets, consideramos a operação do filtro para remover ruídos de alta frequência:
Listagem import pandas as pd import scaleogram as scg from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values discrete_wavelets =[('db38', 5),('db1',11)] for v in discrete_wavelets: def lowpassfilter(signal, thresh = 0.63, wavelet=v[0]): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal wavelet = pywt.DiscreteContinuousWavelet(v[0]) phi, psi, x = wavelet.wavefun(level=v[1]) fig, ax = subplots(figsize=(8,4)) ax.set_title(" : %s,level=%s"%(v[0],v[1]), fontsize=12) ax.plot(x,phi,linewidth=2) fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'r', label='DWT ', linewidth=2) ax.legend() ax.set_title(' \n :%s,level=%s'%(v[0],v[1]),fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) wavelet = 'cmor1-0.5' ax = ax = scg.cws(rec, scales=arange(1,128), wavelet=wavelet,figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT \n( DWT )') show()

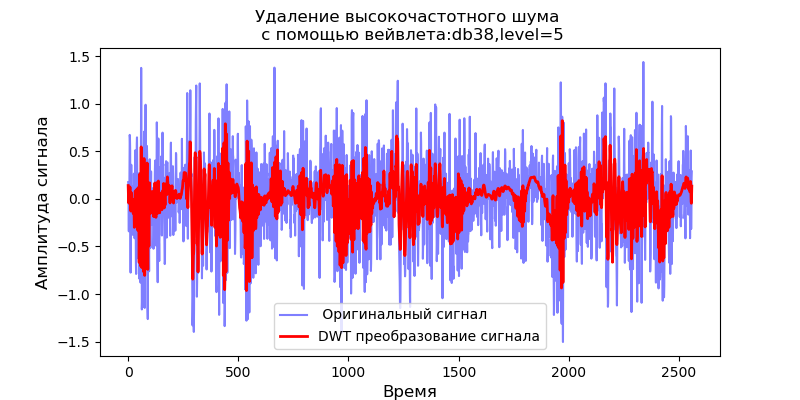
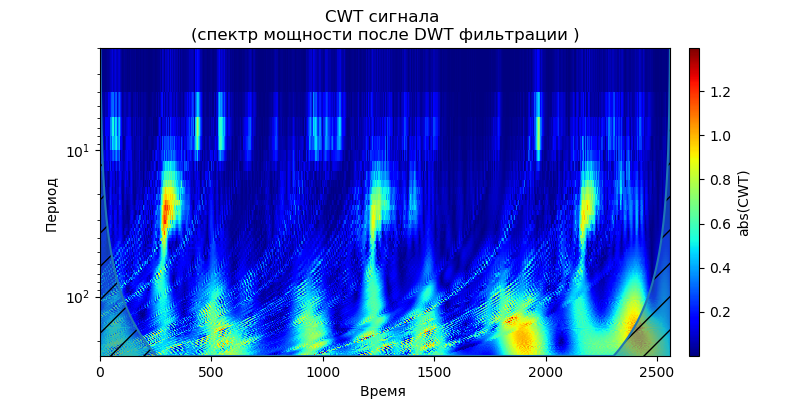

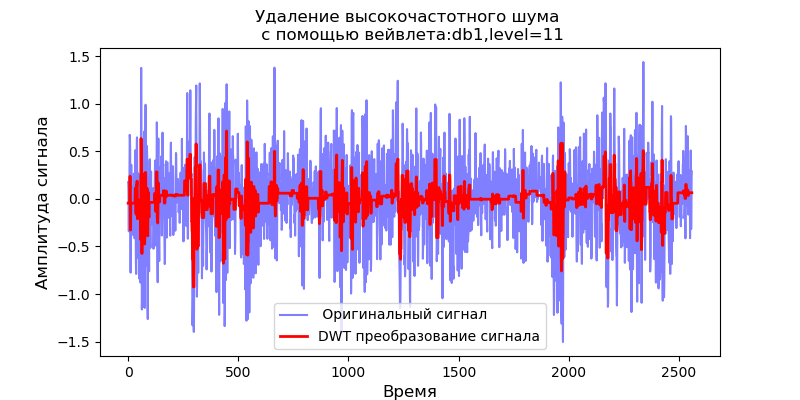

Segue-se das formas de onda citadas dos sinais na saída do filtro que, para a wavelet db38, o pico de potência do espectro é seguido por regiões localizadas, para a wavelet db1 essas regiões desaparecem. Deve-se notar que, por exemplo, a wavelet db38 pode se aproximar de um sinal de polinômio de grau 37. Isso estende a classificação dos sinais, por exemplo, para identificar falhas no equipamento pelos sinais dos sensores de vibração.
Como o sinal após o filtro com a wavelet de Daubechies forma uma série temporal usando os coeficientes de aproximação e decomposição como características das séries, pode-se determinar o grau de proximidade dessas séries, o que simplifica bastante sua pesquisa e classificaçãoFiltro Kalman para remover ruídos de alta frequência
O filtro Kalman é amplamente utilizado para filtrar ruídos em vários sistemas dinâmicos. Considere um sistema dinâmico com um vetor de estado x.
x=F cdotx+w(Q)onde F é a matriz de transição
w (Q) é um processo aleatório (ruído) com zero expectativa matemática e uma matriz de covariância Q.
Observaremos as transições de estado do sistema com um erro de medição conhecido a cada momento. A remoção do ruído usando o método Kalman consiste em duas etapas - extrapolação e correção, é assim.
Defina os parâmetros do sistema:
Matriz Q da covariância do ruído (covariância do ruído do processo).
H é a matriz de observação (medição).
R - covariância do ruído de observação (covariância do ruído de medição).
P = Q é o valor inicial da matriz de covariância para o vetor de estado.
z (t) é o estado observado do sistema.
x = z (0) é o valor inicial da avaliação do estado do sistema.
Para cada observação z, calcularemos o estado filtrado x
e para isso, executamos as seguintes etapas.
• passo 1: extrapolação
1. extrapolação (previsão) do estado do sistema
x=F cdotx2. calcular a matriz de covariância para o vetor de estado extrapolado
F=F cdotP cdotFT+Q• passo 2: correção
1. calcular o vetor de erro, o desvio da observação do estado esperado
y=z−H cdotx2. calcular a matriz de covariância para o vetor de desvio (vetor de erro)
S=H cdotP cdotHT+R3. calcular os ganhos de Kalman
K=P cdotH cdotHT cdotS−14. correção da estimativa do vetor de estado
x=x+K cdoty5. corrigimos a matriz de covariância para estimar o vetor de estado do sistema
P=(I−K cdotH) cdotPListagem para a implementação do algoritmo from scipy import* from pylab import* import pandas as pd def kalman_filter( z, F = eye(2), # (transitionMatrix) Q = eye(2)*3e-3, # (processNoiseCov) H = eye(2), # (measurement) R = eye(2)*3e-1 # (measurementNoiseCov) ): n = z.shape[0]
Para o modelo dinâmico fornecido, você pode usar a biblioteca pyKalman:
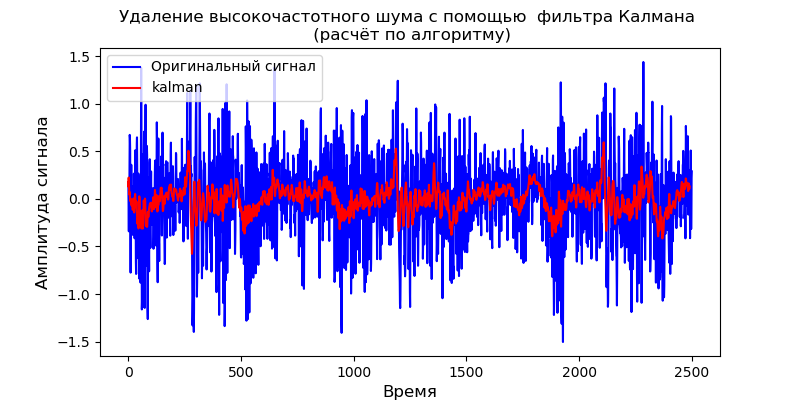
Listagem from pykalman import KalmanFilter import pandas as pd from pylab import * import scaleogram as scg filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values measurements =signal kf = KalmanFilter(transition_matrices=[1] ,



O filtro Kalman remove bem o ruído de alta frequência, no entanto, não permite alterar a forma do sinal de saída.
Método de média móvel
Ao determinar a direção principal das mudanças em uma sequência fortemente oscilante, surge o problema de suavizá-la usando o método da média móvel. Podem ser as leituras do sensor de nível de combustível no carro ou, como no nosso caso, os dados dos sensores de alta frequência com relação à degradação acelerada dos rolamentos. O problema pode ser considerado como a restauração de alguma sequência r na qual o ruído foi sobreposto.
Média Móvel Simples para curto - SMA (Média Móvel Simples). Para calcular o valor atual do filtro
ri apenas calculamos a média dos n elementos anteriores da sequência, para que o filtro comece a trabalhar com o elemento da sequência n.
ri= frac1n cdot sumnj=1e(i−j);i>nListagem <source lang="python">from scipy import * import pandas as pd from pylab import * import pywt import scaleogram as scg def get_ave_values(xvalues, yvalues, n = 6): signal_length = len(xvalues) if signal_length % n == 0: padding_length = 0 else: padding_length = n - signal_length//n % n xarr = array(xvalues) yarr = array(yvalues) xarr.resize(signal_length//n, n) yarr.resize(signal_length//n, n) xarr_reshaped = xarr.reshape((-1,n)) yarr_reshaped = yarr.reshape((-1,n)) x_ave = xarr_reshaped[:,0] y_ave = nanmean(yarr_reshaped, axis=1) return x_ave, y_ave def plot_signal_plus_average(time, signal, average_over = 5): fig, ax = subplots(figsize=(8, 4)) time_ave, signal_ave = get_ave_values(time, signal, average_over) ax.plot(time_ave, signal_ave,"b", label = ' (n={})'.format(5)) ax.set_xlim([time[0], time[-1]]) ax.set_ylabel(' ', fontsize=12) ax.set_title(' SMA', fontsize=14) ax.set_xlabel('', fontsize=12) ax.legend() return signal_ave filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) df_nino = df[4].values N = df_nino.shape[0] time = arange(0, N) signal = df_nino signal_ave=plot_signal_plus_average(time, signal) wavelet = 'cmor1-0.5' ax = ax = scg.cws(signal, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4),cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT %s \n( )'%filename) ax = ax = scg.cws(signal_ave, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT %s \n( )'%filename) show()

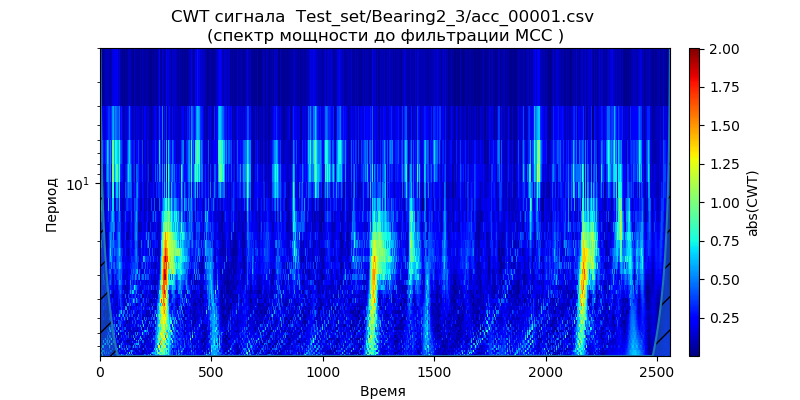

Como se segue no escalograma, o método SMA limpa mal o sinal do ruído de alta frequência e
como mencionado acima é usado para suavizar.
Conclusões:
- Usando o módulo de escalograma, foram obtidos escalogramas de wavelets CWT de três sinais de sensor de vibração de teste para diferentes condições de teste para rolamentos do mesmo tipo. De acordo com os dados do escalograma, um sinal com sinais claramente expressos de degradação tardia foi selecionado. Este sinal foi usado para demonstrar a operação dos filtros em todos os exemplos dados.
- Os métodos da biblioteca PyWavelets para desconstrução de DWT e restauração do sinal do sensor de vibração usando os módulos pywt.dwt (), pywt.idwt () e o módulo pywt.wavedec () para um determinado nível de wavelet são considerados.
- Os exemplos mostram os recursos de aplicativo do módulo pywt.threshol () para filtrar os coeficientes de refinamento DWT, responsáveis pela parte de alta frequência do espectro usando funções de limite para um determinado valor de limite.
- São considerados os efeitos da wavelet antiderivada DWT na forma de um sinal limpo de ruído.
- É obtido um modelo de filtro Kalman para um meio dinâmico; o modelo é testado no sinal de teste do sensor de vibração. O gráfico de remoção de ruído é igual ao obtido usando o módulo pyKalman. A natureza do gráfico coincide com o escalograma.
- .