
A tradução do artigo foi preparada especialmente para os alunos do curso "Algoritmos para Desenvolvedores" .
A classificação em pirâmide (ou classificação de heap, HeapSort) é um método de classificação de comparação com base em uma estrutura de dados, como um heap binário. É semelhante à classificação por seleção, onde primeiro procuramos o elemento máximo e o colocamos no final. Em seguida, repetimos a mesma operação para os elementos restantes.
Vamos primeiro definir uma árvore binária completa. Uma árvore binária concluída é uma árvore binária na qual cada nível, com a possível exceção do último, possui um conjunto completo de nós e todas as folhas estão localizadas à esquerda ( Wikipedia da fonte).
Um heap binário é uma árvore binária completa na qual os elementos são armazenados em uma ordem especial: o valor no nó pai é maior que (ou menor que) os valores em seus dois nós filhos. A primeira opção é chamada max-heap e a segunda é min-heap. Um heap pode ser representado por uma árvore binária ou uma matriz.
Por que a representação baseada em matriz é usada para heap binário?
Como o heap binário é uma árvore binária completa, ele pode ser facilmente representado como uma matriz, e a representação baseada em matriz é eficiente em termos de consumo de memória. Se o nó pai estiver armazenado no índice I, o filho esquerdo pode ser calculado como 2 I + 1 e o filho direito pode ser calculado como 2 I + 2 (desde que a indexação inicie em 0).
Algoritmo de classificação piramidal em ordem crescente:
- Crie max-heap a partir da entrada.
- Nesse estágio, o maior elemento é armazenado na raiz do heap. Substitua-o pelo último elemento do heap e reduza seu tamanho em 1. Finalmente, converta a árvore resultante no heap max com uma nova raiz.
- Repita as etapas acima até que o tamanho da pilha seja maior que 1.
Como construir um monte?
O procedimento de conversão de heap (a seguir denominado procedimento de heapify) pode ser aplicado a um nó somente se seus nós filhos já estiverem convertidos. Assim, a conversão deve ser realizada de baixo para cima. Vamos descobrir com um exemplo:
: 4, 10, 3, 5, 1 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) . heapify 1: 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) heapify 0: 10(0) / \ 5(1) 3(2) / \ 4(3) 1(4) heapify .
Recomendação: resolva o problema de “PRÁTICA” antes de prosseguir com a solução .
C ++
// C++ #include <iostream> using namespace std; // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { swap(arr[i], arr[largest]); // heapify(arr, n, largest); } } // , void heapSort(int arr[], int n) { // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // swap(arr[0], arr[i]); // heapify heapify(arr, i, 0); } } /* n*/ void printArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } // int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); }
Java
// Java public class HeapSort { public void sort(int arr[]) { int n = arr.length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } // public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6, 7}; int n = arr.length; HeapSort ob = new HeapSort(); ob.sort(arr); System.out.println("Sorted array is"); printArray(arr); } }
Python
# Python # i, arr[]. n - def heapify(arr, n, i): largest = i # Initialize largest as root l = 2 * i + 1 # left = 2*i + 1 r = 2 * i + 2 # right = 2*i + 2 # , if l < n and arr[i] < arr[l]: largest = l # , if r < n and arr[largest] < arr[r]: largest = r # , if largest != i: arr[i],arr[largest] = arr[largest],arr[i] # # heapify . heapify(arr, n, largest) # def heapSort(arr): n = len(arr) # max-heap. for i in range(n, -1, -1): heapify(arr, n, i) # for i in range(n-1, 0, -1): arr[i], arr[0] = arr[0], arr[i] # heapify(arr, i, 0) # arr = [ 12, 11, 13, 5, 6, 7] heapSort(arr) n = len(arr) print ("Sorted array is") for i in range(n): print ("%d" %arr[i]), # Mohit Kumra
C afiado
// C# using System; public class HeapSort { public void sort(int[] arr) { int n = arr.Length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int[] arr, int n, int i) { int largest = i; // int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int[] arr) { int n = arr.Length; for (int i=0; i<n; ++i) Console.Write(arr[i]+" "); Console.Read(); } // public static void Main() { int[] arr = {12, 11, 13, 5, 6, 7}; int n = arr.Length; HeapSort ob = new HeapSort(); ob.sort(arr); Console.WriteLine("Sorted array is"); printArray(arr); } } // // Akanksha Ra (Abby_akku)
Php
<?php // Php // i, // arr[]. n - function heapify(&$arr, $n, $i) { $largest = $i; // $l = 2*$i + 1; // = 2*i + 1 $r = 2*$i + 2; // = 2*i + 2 // if ($l < $n && $arr[$l] > $arr[$largest]) $largest = $l; // , if ($r < $n && $arr[$r] > $arr[$largest]) $largest = $r; // if ($largest != $i) { $swap = $arr[$i]; $arr[$i] = $arr[$largest]; $arr[$largest] = $swap; // heapify($arr, $n, $largest); } } // , function heapSort(&$arr, $n) { // ( ) for ($i = $n / 2 - 1; $i >= 0; $i--) heapify($arr, $n, $i); // for ($i = $n-1; $i >= 0; $i--) { // $temp = $arr[0]; $arr[0] = $arr[$i]; $arr[$i] = $temp; // heapify heapify($arr, $i, 0); } } /* n */ function printArray(&$arr, $n) { for ($i = 0; $i < $n; ++$i) echo ($arr[$i]." ") ; } // $arr = array(12, 11, 13, 5, 6, 7); $n = sizeof($arr)/sizeof($arr[0]); heapSort($arr, $n); echo 'Sorted array is ' . "\n"; printArray($arr , $n); // Shivi_Aggarwal ?>
Conclusão:
: 5 6 7 11 12 13
Aqui está o código C anterior para referência.
Observações:
A classificação piramidal é um algoritmo perfeitamente adequado. Sua implementação típica não é estável, mas pode ser feita como tal (veja aqui ).
Complexidade de tempo: a complexidade de tempo do heapify é O (Logn). A complexidade de tempo de createAndBuildHeap () é O (n) e o tempo de execução total da classificação em pirâmide é O (nLogn).
Aplicações de classificação piramidal:
- Classifique uma matriz quase classificada (ou ordenada por K posições) ;
- k elementos maiores (ou menores) da matriz .
O algoritmo de classificação piramidal tem uso limitado, porque o Quicksort e o Mergesort são melhores na prática. No entanto, a própria estrutura de dados da pilha é usada com bastante frequência. Consulte Aplicativos de estrutura de dados de heap
Imagens:
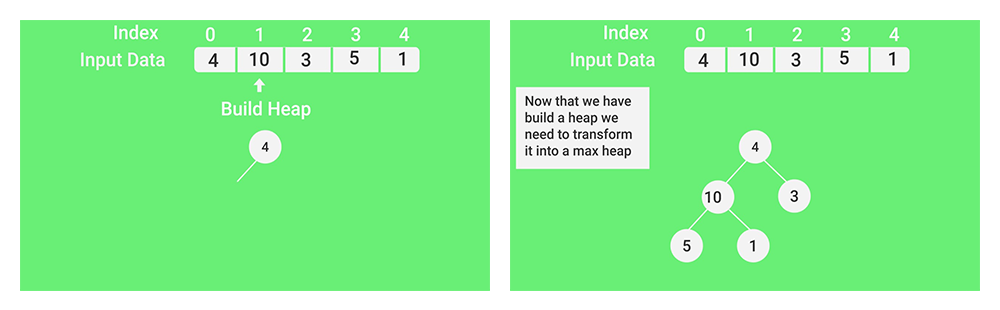
- (Agora que criamos o heap, precisamos convertê-lo para max-heap)

- (No heap máximo, o nó pai é sempre maior ou igual aos nós filhos
10 mais que 4. Portanto, trocamos 4 e 10)
- (No heap máximo, o nó pai é sempre maior ou igual aos nós filhos
5 mais 4. Portanto, trocamos de lugar 5 e 4)

- (Troque o primeiro e o último nó e exclua o último da pilha)
Teste de pirâmide
Outros algoritmos de classificação no GeeksforGeeks / GeeksQuiz:
Classificação rápida , Classificação por seleção , Classificação por bolha , Classificação por inserção , Classificação por mesclagem , Classificação por pirâmide , Classificação por bits , Classificação por contagem , Classificação por bloco , Classificação por shell , Classificação por pente, Classificação por pente, Classificação por contagem com lista .
Oficina de classificação
Deixe comentários se encontrar algo errado ou quiser compartilhar informações adicionais sobre o tópico discutido acima.