O universo de tarefas controladas por computador cresceu. Graças a qual ingrediente secreto isso aconteceu? Devido ao emaranhamento quântico.

Imagine que alguém veio até você e disse que ele tem um oráculo que pode revelar os segredos secretos do universo. Você pode estar interessado nisso, mas seria difícil para você acreditar. Você gostaria de encontrar uma maneira de confirmar que o oráculo está dizendo a verdade.
Este é o principal problema da ciência da computação. Algumas tarefas são muito difíceis de resolver em um período de tempo razoável. Mas suas decisões são fáceis de verificar. Diante disso, os cientistas da computação querem saber: quão complexa pode ser uma tarefa, cuja solução ainda pode ser verificada?
Acontece que a resposta a essa pergunta é: quase inimaginavelmente complexa.
Em um
artigo publicado em abril de 2019, dois especialistas em ciência da computação aumentaram radicalmente o número de tarefas que se enquadram na categoria "difícil de resolver, fácil de verificar". Eles descrevem um método que permite verificar soluções para problemas de complexidade quase incompreensível. "Parece loucura", disse Thomas Widick, especialista em TI do Instituto de Tecnologia da Califórnia que não está envolvido neste trabalho.
O estudo é aplicável a computadores quânticos que realizam cálculos de acordo com as regras não intuitivas da mecânica quântica. Os computadores quânticos mal apareceram, mas no futuro eles têm o potencial de revolucionar a computação.
O novo trabalho, de fato, nos dá influência sobre esse oráculo todo-poderoso. Mesmo que o oráculo prometa fornecer soluções prontas para problemas cujas possibilidades de solução estão muito além de suas capacidades, ainda resta uma maneira de verificar se o oráculo está dizendo a verdade.
Para o fim do universo
Quando um problema é difícil de resolver, mas fácil de verificar, encontrar uma solução leva muito tempo, mas verificar a correção de uma solução específica não. Por exemplo, suponha que uma pessoa mostre um gráfico - um conjunto de pontos (vértices) conectados por linhas (arestas). Uma pessoa pergunta se é possível colorir os vértices do gráfico com três cores, para que nenhum dos dois vértices conectados tenha a mesma cor.
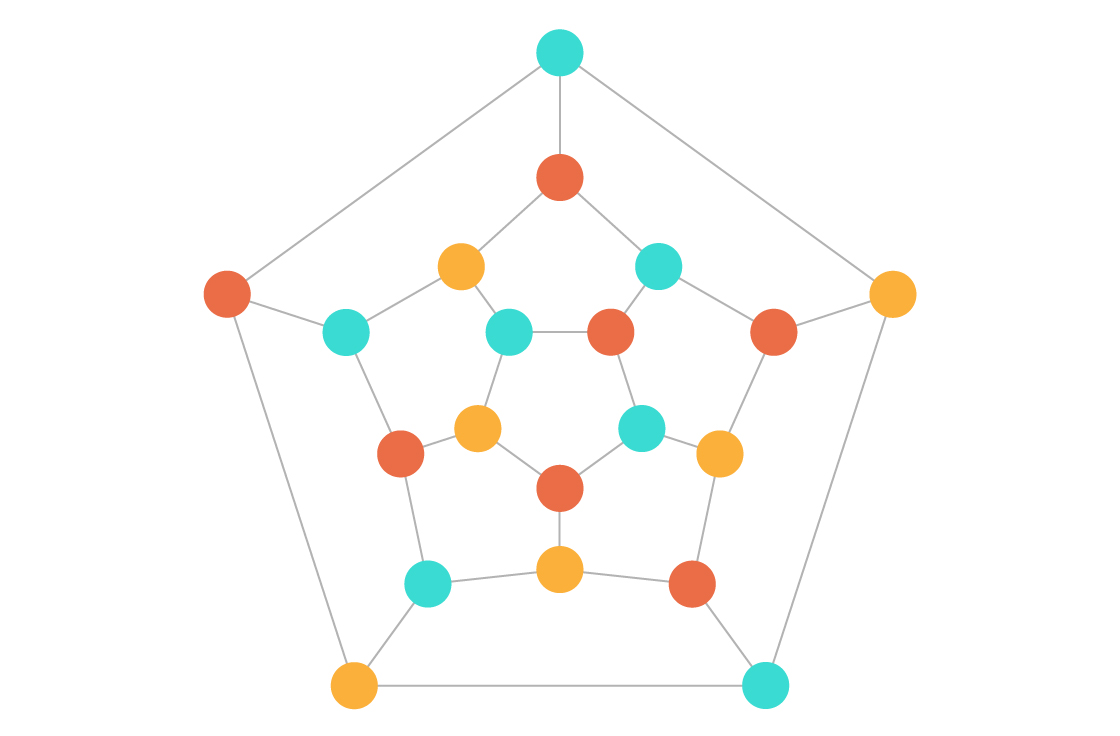
A tarefa de três cores é difícil de resolver. No caso geral, o tempo necessário para procurar a coloração dos vértices (ou determinar que essa coloração não existe) aumenta exponencialmente com o aumento do tamanho do gráfico. Se, por exemplo, a busca de uma solução para um gráfico com 20 vértices levar 3
20 ns - ou seja, alguns segundos, para um gráfico com 60 vértices, serão necessários 3
60 ns, que é 100 vezes a idade atual do Universo.
Mas digamos que alguém alega ter pintado a contagem com três cores. A verificação deste aplicativo não levará muito tempo. Você só precisa percorrer todos os vértices um a um, estudando os vértices associados a eles. À medida que o tamanho do gráfico aumenta, o tempo dessa verificação aumenta lentamente - como
polinômio . Como resultado, o computador não leva muito mais tempo para verificar a coloração de um gráfico de 60 vértices do que para verificar um gráfico de 20 vértices.
"Com a cor certa em três cores, é fácil testar seu desempenho", disse
John Wright , físico do Instituto de Tecnologia de Massachusetts, que escreveu esse trabalho junto com
Anand Natarajan, da Caltech.
Na década de 1970, os cientistas da computação determinaram uma classe de tarefas fáceis de verificar, mesmo que algumas delas sejam difíceis de resolver. Eles chamaram essa classe NP de
tempo polinomial não determinístico . Desde então, na ciência da computação, a classe NP tem sido estudada mais do que outras. Em particular, os cientistas da computação gostariam de saber como essa classe muda quando o algoritmo de teste recebe novas maneiras de verificar a correção da solução.
Perguntas certas
Antes do trabalho de Natarajan e Wright, o poder das inspeções aumentou em dois grandes saltos.
Para entender o primeiro, imagine que você não faz distinção entre cores. Alguém coloca dois cubos em cima da mesa à sua frente e pergunta se eles são da mesma cor ou são diferentes. Esta tarefa é impossível para você. Além disso, você não pode confirmar a correção da solução de outra pessoa para esse problema.
No entanto, você pode fazer perguntas a essa pessoa que prova. Suponha que o provador lhe diga que os cubos são de cores diferentes. Você chama um deles de "Cubo A" e o outro "Cubo B". Então você os esconde pelas costas e acidentalmente troca de lugar entre eles. Então você abre os cubos e pede ao provador que encontre o dado A.
Se os cubos são de cores diferentes, essa é uma pergunta muito simples. O provador reconhecerá o Cubo A, se este for, digamos, um cubo vermelho, e o determinará corretamente a cada vez.
No entanto, se os cubos são da mesma cor - e o provador errou ao chamá-los de diferentes - o provador só pode adivinhar qual é qual. Portanto, ele poderá determinar corretamente o cubo A apenas em 50% dos casos. Ao questionar constantemente o provador sobre sua decisão, você pode confirmar se está correto.
 Anand Natarajan e John Wright
Anand Natarajan e John Wright"O examinador pode enviar perguntas ao provador", disse Wright, "e talvez no final da conversa, o examinador fique mais convencido da resposta."
Em 1985, três cientistas da computação provaram que essa evidência interativa pode ser usada para confirmar soluções para problemas mais complexos do que os problemas da NP. O trabalho deles criou uma nova classe de tarefas, IP, "tempo polinomial interativo". O método usado para confirmar as cores dos cubos pode ser usado para confirmar respostas a perguntas muito mais complexas.
O segundo avanço ocorreu na mesma década. Parece a lógica de uma investigação policial. Se você tem dois suspeitos que cometeram, na sua opinião, um crime, não os interrogará juntos. Você as interrogará em salas diferentes e comparará as respostas de uma com as respostas da outra. Ao entrevistá-los individualmente, você pode revelar mais verdade do que se tivesse um suspeito.
"Os dois suspeitos não serão capazes de criar uma história consistente distribuída, porque não sabem quais são as outras respostas", disse Wright.
Em 1988, quatro cientistas da computação provaram que, se você pedir a dois computadores para resolver o mesmo problema separadamente e depois questioná-los separadamente, poderá confirmar uma classe de problemas ainda maior que o IP: a classe MIP, evidência interativa com muitas evidências.
Usando essa abordagem, é possível, por exemplo, confirmar a correção de colorir um gráfico em três cores para uma sequência de gráficos que aumentam de tamanho muito mais rapidamente do que os gráficos do NP. No NP, os tamanhos dos gráficos aumentam linearmente - o número de vértices pode aumentar de 1 para 2, até 3, até 4 e assim por diante - para que o tamanho do gráfico não seja desproporcionalmente maior que o tempo necessário para verificar a coloração. Mas no MIP, o número de vértices do gráfico cresce exponencialmente de 2
1 para 2
2 , 2
3 , 2
4 e assim por diante.
Como resultado, os gráficos são grandes demais para caber na memória do computador, que deve passar pela lista de vértices e verificar a coloração. No entanto, a coloração ainda pode ser verificada perguntando aos dois provadores perguntas diferentes, mas relacionadas.
No MIP, o testador possui memória suficiente para executar um programa que nos permite determinar se dois vértices do gráfico estão conectados por uma aresta - e ele pode verificar as respostas dos testadores para garantir que a cor esteja correta.
Expandir a lista de tarefas difíceis de resolver, mas fáceis de verificar, de computadores clássicos para NP, IP e MIP. Mas os computadores quânticos funcionam de maneira muito diferente. E por várias décadas não ficou claro como o uso deles muda esse quadro - é mais fácil ou mais difícil verificar soluções com a ajuda deles?
O novo trabalho de Natarajan e Wright tem a resposta para esta pergunta.
Truques quânticos
Computadores quânticos realizam cálculos com bits quânticos ou qubits. Eles têm uma propriedade como
emaranhamento um com o outro. E quando dois qubits - ou mesmo grandes sistemas de qubit - são confundidos, isso significa que suas propriedades físicas de certa maneira se afetam.
Em seu novo trabalho, Natarajan e Wright consideram um cenário que inclui dois computadores quânticos diferentes, com os qubits de um confundidos com os qubits do outro.
Parece que essa configuração piora a qualidade da verificação da resposta. O poder total da evidência interativa com muitos provadores decorre precisamente do fato de que você pode entrevistar dois provadores separadamente e verificar suas respostas. Se as respostas dos provadores forem as mesmas, é provável que sejam verdadeiras. Mas se os estados quânticos de dois provadores estiverem confusos, eles pareceriam ter mais oportunidades de insistir consistentemente na correção de respostas incorretas.
De fato, quando o cenário com dois computadores quânticos emaranhados foi
revelado pela primeira
vez em 2003, os cientistas da computação sugeriram que o emaranhamento reduziria a possibilidade de verificação. "A reação óbvia de todos, incluindo a minha, foi que os provadores nesse caso tiveram mais oportunidades", disse Vidik. "Eles podem usar a confusão para vincular suas respostas."
Mas, apesar do pessimismo inicial, Vidik passou vários anos tentando provar o contrário. Em 2012, ele e
Tsuyoshi Ito provaram que existe a capacidade de testar todas as tarefas no MIP usando computadores quânticos emaranhados.
Agora, Natarajan e Wright provaram que a situação é ainda melhor: com a ajuda da complexidade, pode-se provar uma classe de problemas ainda maior do que sem ela. É possível reverter a conexão entre computadores quânticos emaranhados em benefício do verificador.
Para entender como fazer isso, lembre-se do procedimento do MIP para verificar a coloração dos gráficos cujos tamanhos crescem exponencialmente. O testador não possui memória suficiente para armazenar o gráfico inteiro, mas possui memória suficiente para determinar dois vértices conectados e fazer uma pergunta aos testadores sobre a cor desses vértices.
Na classe de problemas considerados por Natarajan e Wright - chamados NEEXP, um tempo não-determinístico duas vezes exponencial - o tamanho dos gráficos cresce ainda mais rápido do que no PIM. Os gráficos no NEEXP crescem na "dupla taxa exponencial". Em vez de crescer como graus de dois - 2
1 , 2
2 , 2
3 , 2
4 e assim por diante - o número de vértices nos gráficos cresce como graus de dois - 2
2 1 , 2
2 2 , 2
2 3 , 2
2 4 e assim por diante. Como resultado, os gráficos rapidamente se tornam tão grandes que o inspetor não consegue mais encontrar um par de vértices conectados.
"Para identificar o vértice, são necessários 2
n bits, o que é exponencialmente mais do que o verificador tem na memória", disse Natarajan. No entanto, Natarajan e Wright provaram que é possível verificar a coloração de um gráfico dupla exponencial em três cores, mesmo sem a capacidade de determinar quais vértices precisam ser solicitados como evidência. O fato é que você pode fazer com que os provadores escolham as perguntas certas.
A idéia de fazer com que os computadores se interroguem sobre suas próprias decisões parece tão razoável para os cientistas quanto pedir aos suspeitos que criminosos se interroguem é definitivamente uma proposta estúpida. Isso é apenas Natarajan e Wright provaram que não é assim. E a razão para isso é confusão.
"Estados emaranhados são recursos compartilhados", disse Wright. "Todo o nosso protocolo é entender como usar esse recurso compartilhado para criar problemas interconectados".
Se os computadores quânticos estiverem confusos, sua escolha de vértices se correlacionará e fornecerá o conjunto certo de perguntas para verificar a coloração em três cores.
Ao mesmo tempo, o inspetor não precisa que os dois computadores quânticos estejam interligados para que suas respostas a essas perguntas sejam correlacionadas entre si (isso seria semelhante à maneira como dois criminosos suspeitos correlacionam seu álibi falso). Outra característica quântica estranha lida com esse problema. Na mecânica quântica,
o princípio da incerteza nos proíbe de conhecer ao mesmo tempo a localização exata e o momento de uma partícula - se você mede uma propriedade, destrói informações sobre outra. O princípio da incerteza limita severamente o seu conhecimento de quaisquer duas propriedades "complementares" de um sistema quântico.
Natarajan e Wright usam isso em seu trabalho. Para calcular a cor do vértice, eles forçam dois computadores quânticos a fazer medições complementares. Cada computador calcula a cor de seu próprio vértice e destrói todas as informações sobre o outro. Em outras palavras, a confusão permite que os computadores façam perguntas correlativas, mas o princípio da incerteza os proíbe de conspirar para respondê-las.
"Precisamos fazer os provadores esquecerem, e isso é a principal coisa que Natarajan e Wright fizeram em seu trabalho", disse Vidik. "Eles forçam o provador a apagar as informações através da medição."
As conseqüências de seu trabalho podem ser chamadas quase existenciais. Antes do lançamento do trabalho, a limitação do conhecimento que podemos obter com total confiança era muito menor. Se nos fosse dada uma resposta para um problema do conjunto da NEEXP, teríamos que aceitá-lo apenas com fé. Mas Natarajan e Wright romperam essas fronteiras e tornaram possível confirmar as respostas de um universo muito maior de problemas computacionais.
E agora que eles fizeram isso, não está claro onde está o próximo limite de verificabilidade. "Poderia ser muito mais longe", disse Lance Fortnau, especialista em TI do Instituto de Tecnologia da Geórgia. "Eles deixam em aberto a oportunidade de dar o próximo passo."