
A ciência de dados está se tornando parte integrante de qualquer atividade de marketing, e este livro é um retrato vivo da transformação digital em marketing. A análise de dados e algoritmos inteligentes automatizam tarefas de marketing demoradas. O processo de tomada de decisão está se tornando não apenas mais perfeito, mas também mais rápido, o que é de grande importância em um ambiente competitivo em constante aceleração.
“Este livro é um retrato vivo da transformação digital em marketing. Ele mostra como a ciência de dados está se tornando parte integrante de qualquer atividade de marketing. Ele descreve em detalhes como abordagens baseadas em análise de dados e algoritmos inteligentes contribuem para a automação profunda de tarefas de marketing tradicionalmente trabalhosas. O processo de tomada de decisão está se tornando não apenas mais avançado, mas também mais rápido, o que é importante em nosso ambiente competitivo em constante aceleração. Este livro deve ser lido por especialistas em processamento de dados e especialistas em marketing, e é melhor se eles lerem juntos. ” Andrey Sebrant, diretor de marketing estratégico da Yandex.
Trecho. 5.8.3 Modelos de fator oculto
Nos algoritmos de filtragem conjunta discutidos até agora, a maioria dos cálculos é baseada nos elementos individuais da matriz de classificação. Os métodos baseados em proximidade avaliam as classificações ausentes diretamente dos valores conhecidos na matriz de classificações. Os métodos baseados em modelo adicionam uma camada de abstração na parte superior da matriz de classificação, criando um modelo preditivo que captura certos padrões de relacionamento entre usuários e elementos, mas o treinamento do modelo ainda é altamente dependente das propriedades da matriz de classificação. Como resultado, essas técnicas de filtragem colaborativa geralmente enfrentam os seguintes problemas:
A matriz de classificação pode conter milhões de usuários, milhões de elementos e bilhões de classificações conhecidas, o que cria sérios problemas de complexidade e escalabilidade computacional.
A matriz de classificação é geralmente muito escassa (na prática, cerca de 99% das classificações podem estar ausentes). Isso afeta a estabilidade computacional dos algoritmos de recomendação e leva a estimativas não confiáveis quando o usuário ou elemento não possui vizinhos realmente semelhantes. Esse problema geralmente é exacerbado pelo fato de que os algoritmos mais básicos são orientados ao usuário ou ao elemento, o que limita sua capacidade de registrar todos os tipos de semelhanças e relacionamentos disponíveis na matriz de classificação.
Os dados na matriz de classificação são geralmente fortemente correlacionados devido a semelhanças entre usuários e elementos. Isso significa que os sinais disponíveis na matriz de classificação são não apenas esparsos, mas também redundantes, o que contribui para a exacerbação do problema de escalabilidade.
As considerações acima indicam que a matriz de classificação original pode não ser a melhor representação de sinais, e outras representações alternativas mais adequadas para a filtragem de juntas devem ser consideradas. Para explorar essa idéia, voltemos ao ponto de partida e pensemos um pouco sobre a natureza dos serviços de recomendação. De fato, o serviço de recomendação pode ser considerado como um algoritmo que prevê classificações com base em alguma medida de similaridade entre o usuário e o elemento:
Uma maneira de determinar essa medida de similaridade é usar a abordagem de fatores ocultos e mapear usuários e elementos para pontos em algum espaço k-dimensional, para que cada usuário e cada elemento seja representado por um vetor k-dimensional:
Os vetores devem ser construídos de modo que as dimensões correspondentes peq sejam comparáveis entre si. Em outras palavras, cada dimensão pode ser considerada como um sinal ou conceito, ou seja, puj é uma medida da proximidade do usuário u e do conceito j, e qij, respectivamente, é uma medida do elemento ie do conceito j. Na prática, essas dimensões são frequentemente interpretadas como gêneros, estilos e outros atributos que se aplicam simultaneamente a usuários e elementos. A semelhança entre o usuário e o elemento e, consequentemente, a classificação pode ser definida como o produto dos vetores correspondentes:

Como cada classificação pode ser decomposta em um produto de dois vetores que pertencem a um espaço conceitual que não é observado diretamente na matriz de classificação original, p e q são chamados de fatores ocultos. O sucesso dessa abordagem abstrata, é claro, depende inteiramente de como os fatores ocultos são determinados e construídos. Para responder a essa pergunta, observamos que a expressão 5.92 pode ser reescrita na forma de matriz da seguinte maneira:
onde P é a matriz n × k montada a partir dos vetores p, e Q é a matriz m × k montada a partir dos vetores q, como mostrado na Fig. 5.13 O principal objetivo de um sistema de filtragem conjunta é geralmente minimizar os erros de previsão da classificação, o que permite determinar diretamente o problema de otimização em relação à matriz de fatores ocultos:
Supondo que o número de dimensões ocultas k seja fixo e k ≤ n e k ≤ m, o problema de otimização 5,94 reduz-se ao problema de aproximação de baixa classificação, que consideramos no Capítulo 2. Para demonstrar a abordagem da solução, vamos assumir por um momento que a matriz de classificação está completa. Nesse caso, o problema de otimização possui uma solução analítica em termos da Decomposição de Valor Singular (SVD) da matriz de classificação. Em particular, usando o algoritmo SVD padrão, a matriz pode ser decomposta no produto de três matrizes:
onde U é a matriz n × n ortonormalizada por colunas, Σ é a matriz diagonal n × m e V é a matriz m × m ortonormalizada por colunas. Uma solução ideal para o problema 5.94 pode ser obtida em termos desses fatores, truncados para as k dimensões mais significativas:
Consequentemente, fatores ocultos que são ótimos em termos de precisão de previsão podem ser obtidos por decomposição singular, como mostrado abaixo:
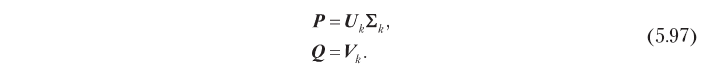
Esse modelo de fator oculto baseado em SVD ajuda a resolver os problemas de co-filtragem descritos no início desta seção. Primeiro, ela substitui a matriz de classificação n × m grande por matrizes de fator n × k e m × k, que geralmente são muito menores, porque, na prática, o número ideal de dimensões ocultas k é geralmente pequeno. Por exemplo, há um caso em que a matriz de classificação com 500.000 usuários e 17.000 elementos foi capaz de ser razoavelmente bem aproximada usando 40 medições [Funk, 2016]. Além disso, o SVD elimina a correlação na matriz de classificação: as matrizes de fatores latentes definidas por 5,97 são ortonormais em colunas, ou seja, as dimensões ocultas não são correlacionadas. Se, o que geralmente é verdade na prática, o SVD também resolve o problema de escassez, porque o sinal presente na matriz de classificação inicial é efetivamente concentrado (lembre-se de que selecionamos k dimensões com a maior energia de sinal) e as matrizes de fator latente não são escassas. A Figura 5.14 ilustra essa propriedade. O algoritmo de proximidade baseado no usuário (5.14, a) recolhe vetores de classificação esparsos para um determinado elemento e um determinado usuário para obter uma pontuação de classificação. O modelo de fator oculto (5.14, b), pelo contrário, estima a classificação por convolução de dois vetores de dimensão reduzida e com maior densidade de energia.

A abordagem descrita acima parece uma solução coerente para o problema dos fatores ocultos, mas, na verdade, apresenta uma séria desvantagem devido à suposição de que a matriz de classificação está completa. Se a matriz de classificação for escassa, o que é quase sempre o caso, o algoritmo SVD padrão não pode ser aplicado diretamente, pois não é capaz de processar elementos ausentes (indefinidos). A solução mais simples nesse caso é preencher as classificações ausentes com algum valor padrão, mas isso pode levar a um sério viés na previsão. Além disso, é computacionalmente ineficiente porque a complexidade computacional de tal solução é igual à complexidade SVD para a matriz n × m completa, enquanto é desejável ter um método com complexidade proporcional ao número de classificações conhecidas. Esses problemas podem ser resolvidos usando os métodos alternativos de decomposição descritos nas seções a seguir.
5.8.3.1 Decomposição ilimitada
O algoritmo SVD padrão é uma solução analítica para o problema de aproximação de baixo escalão. No entanto, esse problema pode ser considerado como um problema de otimização, e também podem ser aplicados métodos de otimização universal. Uma das abordagens mais simples é usar o método de descida de gradiente para refinar iterativamente os valores de fatores ocultos. O ponto de partida é a definição da função de custo J como o erro de previsão residual:
Observe que desta vez não impomos restrições, como a ortogonalidade, à matriz de fatores ocultos. Calculando o gradiente da função de custo em relação a fatores ocultos, obtemos o seguinte resultado:
onde E é a matriz de erro residual:
O algoritmo de descida do gradiente minimiza a função de custo movendo-se em cada etapa na direção negativa do gradiente. Portanto, você pode encontrar fatores ocultos que minimizam o erro quadrado da previsão de classificação alterando iterativamente as matrizes P e Q para convergir, de acordo com as seguintes expressões:

onde α é a velocidade de aprendizado. A desvantagem do método de descida de gradiente é a necessidade de calcular toda a matriz de erros residuais e alterar simultaneamente todos os valores dos fatores ocultos em cada iteração. Uma abordagem alternativa, que pode ser mais adequada para matrizes grandes, é a descida estocástica do gradiente [Funk, 2016]. O algoritmo de descida do gradiente estocástico usa o fato de que o erro total de previsão J é a soma dos erros de elementos individuais da matriz de classificação; portanto, o gradiente geral J pode ser aproximado por um gradiente em um ponto de dados e os fatores ocultos podem ser alterados em termos de elementos. A implementação completa dessa idéia é mostrada no algoritmo 5.1.

O primeiro estágio do algoritmo é a inicialização da matriz de fatores ocultos. A escolha desses valores iniciais não é muito importante, mas, neste caso, é escolhida uma distribuição uniforme da energia das classificações conhecidas entre os fatores ocultos gerados aleatoriamente. Em seguida, o algoritmo otimiza sequencialmente as dimensões do conceito. Para cada medição, ele percorre repetidamente todas as classificações no conjunto de treinamento, prediz cada classificação usando os valores atuais dos fatores ocultos, estima o erro e corrige os valores dos fatores de acordo com as expressões 5.101. A otimização da medição é concluída quando a condição de convergência é atendida, após o que o algoritmo prossegue para a próxima medição.
O algoritmo 5.1 ajuda a superar as limitações do método SVD padrão. Ele otimiza fatores ocultos percorrendo pontos de dados individuais e, assim, evitando problemas com classificações ausentes e operações algébricas com matrizes gigantes. A abordagem iterativa também torna a descida do gradiente estocástico mais conveniente para aplicações práticas do que a descida do gradiente, que modifica matrizes inteiras usando as expressões 5.101.
EXEMPLO 5.6
De fato, uma abordagem baseada em fatores ocultos é um grupo inteiro de métodos de ensino de representações que podem identificar padrões implícitos na matriz de classificação e representá-los explicitamente na forma de conceitos. Às vezes, os conceitos têm uma interpretação completamente significativa, especialmente de alta energia, embora isso não signifique que todos os conceitos sempre tenham um significado significativo. Por exemplo, a aplicação do algoritmo de decomposição da matriz a um banco de dados de classificações de filmes pode criar fatores que correspondem aproximadamente a dimensões psicográficas, como melodrama, comédia, horror etc. Vamos ilustrar esse fenômeno com um pequeno exemplo numérico que usa a matriz de classificação da Tabela. 5.3:

Primeiro, subtraia a média global μ = 2,82 de todos os elementos para centralizar a matriz e, em seguida, execute o algoritmo 5.1 com k = 3 medições ocultas e a taxa de aprendizado α = 0,01 para obter as duas seguintes matrizes de fatores:

Cada linha nessas matrizes corresponde a um usuário ou um filme, e todos os 12 vetores de linha são mostrados na Fig. 5.15 Observe que os elementos na primeira coluna (o primeiro vetor de conceitos) têm os maiores valores e os valores nas colunas subsequentes diminuem gradualmente. Isso é explicado pelo fato de que o primeiro vetor conceitual captura tanta energia de sinal quanto possível de capturar com uma medição, o segundo vetor conceitual captura apenas parte da energia residual, etc. Além disso, observe que o primeiro conceito pode ser semanticamente interpretado como o eixo do drama. - filme de ação, onde a direção positiva corresponde ao gênero do filme de ação, e o negativo - ao gênero do drama. As classificações neste exemplo são altamente correlacionadas, portanto, pode-se ver claramente que os três primeiros usuários e os três primeiros filmes têm grandes valores negativos no primeiro vetor conceitual (filmes de drama e usuários que gostam de tais filmes), enquanto os três últimos usuários e os três últimos os filmes têm ótimos significados positivos na mesma coluna (filmes de ação e usuários que preferem esse gênero). A segunda dimensão nesse caso em particular corresponde principalmente ao viés do usuário ou elemento, que pode ser interpretado como um atributo psicográfico (criticidade dos julgamentos do usuário? Popularidade do cinema?). Outros conceitos podem ser considerados como ruído.
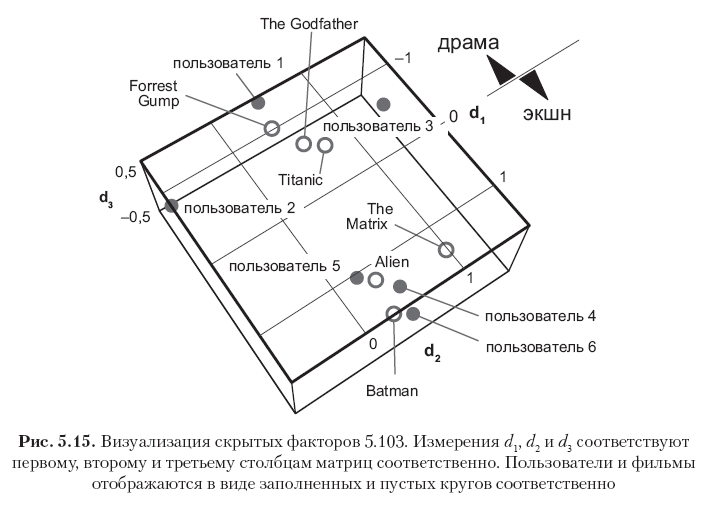
A matriz de fatores resultante não é completamente ortogonal nas colunas, mas tende a ser ortogonal, porque isso decorre da otimização da solução SVD. Isso pode ser visto observando os produtos PTP e QTQ, que são próximos das matrizes diagonais:
As matrizes 5.103 são essencialmente um modelo preditivo que pode ser usado para avaliar classificações conhecidas e ausentes. É possível obter estimativas multiplicando dois fatores e adicionando de volta a média global:
Os resultados reproduzem com precisão o conhecido e preveem as classificações ausentes de acordo com as expectativas intuitivas. A precisão das estimativas pode ser aumentada ou diminuída alterando o número de medições, e o número ideal de medições pode ser determinado na prática através da verificação cruzada e da escolha de um compromisso razoável entre complexidade e precisão computacional.
»Mais informações sobre o livro podem ser encontradas no
site do editor»
Conteúdo»
TrechoCupom de desconto de 25% para vendedores ambulantes -
Machine LearningApós o pagamento da versão impressa do livro, um livro eletrônico é enviado por e-mail.