Palestra "Fundamentos do Processamento Digital de Sinais"

Olá pessoal!

Muitas vezes, as pessoas recorrem a mim com perguntas sobre tarefas do campo de processamento de sinal digital (DSP). Digo em detalhes as nuances, sugiro as fontes de informação necessárias. Mas todos os ouvintes, como o tempo demonstrou, carecem de tarefas e exemplos práticos no processo de aprendizado desta área. A esse respeito, decidi escrever um pequeno curso interativo sobre processamento de sinais digitais e colocá-lo em domínio público .

A maior parte do material de treinamento para apresentação visual e interativa é implementada usando o Jupyter Notebook . Supõe-se que o leitor tenha conhecimento básico do campo da matemática superior, bem como um pequeno comando da linguagem de programação Python.

Lista de palestras

Este curso contém materiais na forma de palestras concluídas sobre vários tópicos da área de processamento de sinal digital. Os materiais são apresentados usando bibliotecas Python (pacotes numpy, scipy, matplotlib, etc.). As informações básicas deste curso foram extraídas de minhas palestras, que eu, como estudante de graduação, dei aos alunos do Instituto de Energia de Moscou (NRU MEI). Parte das informações dessas palestras foi usada em seminários de treinamento no Center for Contemporary Electronics , onde eu atuava como palestrante. Além disso, este material inclui a tradução de vários artigos científicos, compilação de informações de fontes confiáveis ​​e literatura sobre processamento de sinais digitais, além de documentação oficial sobre pacotes de aplicativos e funções internas das bibliotecas scipy e numpy do Python.

Para usuários do MATLAB (GNU Octave), não é difícil dominar o material do ponto de vista do código do programa, pois as principais funções e seus atributos são amplamente idênticos e semelhantes aos métodos das bibliotecas Python.

Todos os materiais são agrupados pelos principais tópicos do processamento de sinal digital:

1. Sinais: analógico, discreto, digital. Conversão Z
2. Transformada de Fourier: amplitude e sinal de fase, DFT e FFT,
3. Convolução e correlação. Convolução linear e cíclica. Convolução rápida
4. Processos aleatórios. Ruído branco. Função densidade de probabilidade
5. Sinais determinísticos. Modulação: AM, FM, FM, LFM. Manipulação
6. Filtro de Sinal: IIR, filtros FIR
7. A janela funciona em tarefas de filtragem. Detecção de sinais fracos.
8. Reamostragem: dizimação e interpolação. Filtros CIC, filtros de média móvel

A lista de palestras é suficiente , mas, é claro, incompleta para um conhecimento introdutório do DSP. Com o tempo livre, pretendo apoiar e desenvolver este projeto.

Onde encontrar?

Todos os materiais são absolutamente gratuitos e disponíveis como repositório aberto no meu github como um projeto de código-fonte aberto . Os materiais são apresentados em dois formatos - na forma de cadernos Jupyter para trabalho interativo, estudo e edição, e na forma de arquivos HTML compilados a partir desses cadernos (após o download no github, eles têm um formato bastante adequado para leitura e impressão).

A seguir, é apresentada uma breve descrição das seções do curso, com breves explicações, termos e definições. Informações básicas estão disponíveis nas palestras iniciais, aqui está apenas uma breve visão geral!

Sinais. Conversão Z

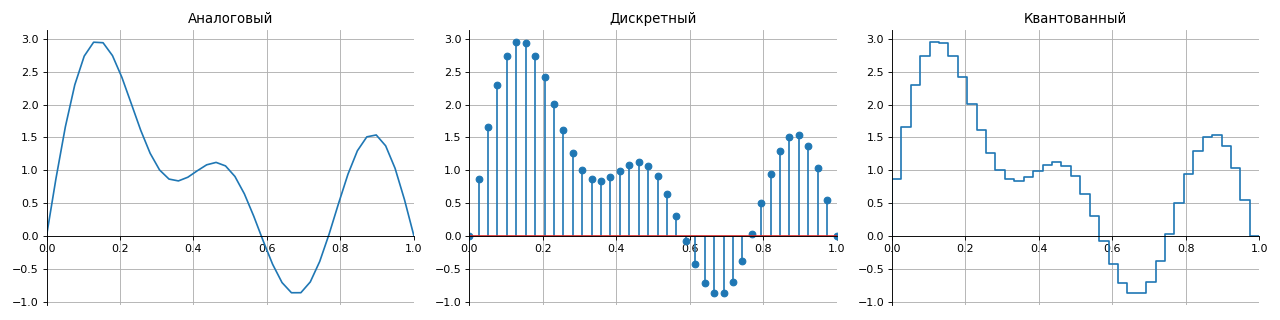
Seção introdutória, que contém informações básicas sobre os tipos de sinais. O conceito de sequência discreta, função delta e função Heaviside (salto unitário) é introduzido.

Todos os sinais de acordo com o método de apresentação no aparelho podem ser divididos em quatro grupos:

• analógico - são descritos por funções contínuas no tempo,
• discreto - são interrompidos no tempo com uma etapa especificada por amostragem,
• quantizado - possui um conjunto de níveis finitos (geralmente em amplitude),
• digital - uma combinação das propriedades de sinais discretos e quantizados.

Para a reconstrução correta de um sinal analógico de um digital sem distorção e perda, é utilizado o teorema de amostragem conhecido como teorema de Kotelnikov (Nyquist-Shannon) .

Qualquer sinal contínuo com um espectro limitado pode ser restaurado de forma única e sem perda de suas amostras discretas, coletadas com uma frequência estritamente maior que o dobro da frequência superior do espectro de um sinal contínuo.

Essa interpretação é válida desde que a função contínua do tempo ocupe uma faixa de frequência de 0 ao valor da frequência superior. Se as etapas de quantização e discretização forem escolhidas incorretamente, o sinal será distorcido de analógico para discreto.

Também nesta seção, a transformação Z e suas propriedades são descritas e a representação de sequências discretas na forma Z é mostrada.

Exemplo de uma sequência discreta finita:

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0} 

.
Um exemplo da mesma sequência no formato Z:

X (z) = 2 + z ^-1 - 2z ^-2 + 2z ^-4 + 3z ^-5 + 1z ^-6

Transformada de Fourier. Propriedades DFT e FFT

Esta seção descreve o conceito do domínio do tempo e da frequência de um sinal. A definição da transformada discreta de Fourier (DFT) é introduzida. As DFTs diretas e inversas e suas principais propriedades são consideradas. É mostrada a transição do DFT para o algoritmo de transformada rápida de Fourier (FFT) na base 2 (algoritmos de dizimação em frequência e tempo). Refletiu a eficácia da FFT em comparação com a DFT.

Em particular, esta seção descreve o pacote Python scipy.ffpack para calcular várias transformadas de Fourier (seno, cosseno, direto, inverso, multidimensional, real).

A transformação de Fourier permite representar qualquer função como um conjunto de sinais harmônicos! A transformada de Fourier é a base dos métodos de convolução e do design de correlacionadores digitais, é usada ativamente na análise espectral e usada ao trabalhar com números longos.

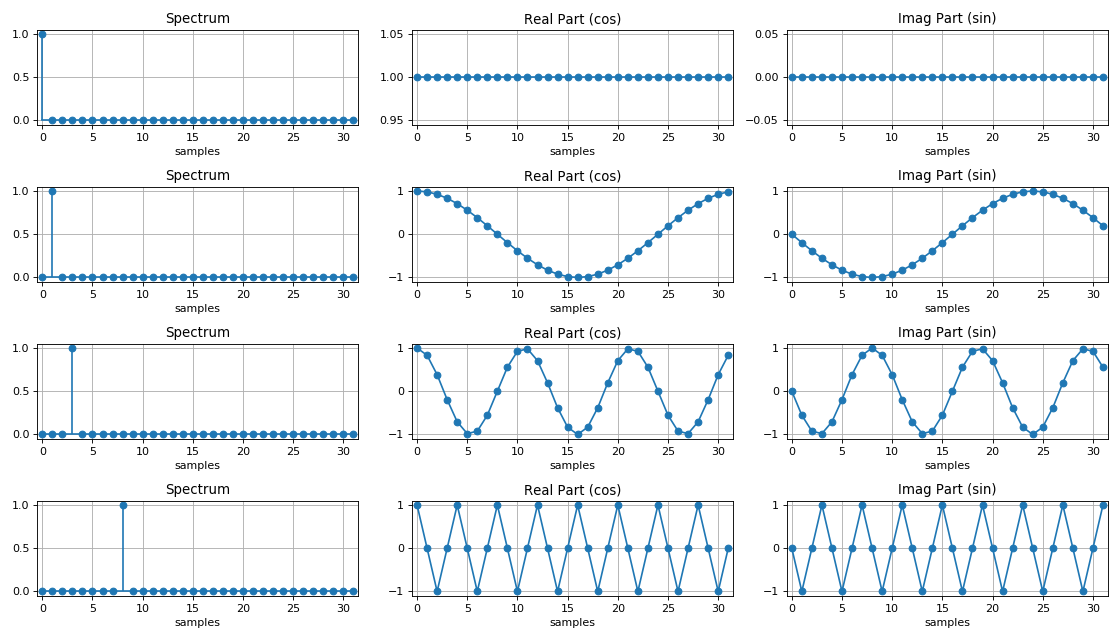
Características dos espectros de sinais discretos:
1. A densidade espectral de um sinal discreto é uma função periódica com um período igual à frequência de amostragem.
2. Se a sequência discreta for real , o módulo de densidade espectral dessa sequência é uma função par e o argumento é uma função de frequência ímpar .

Espectro de Sinal Harmônico:

Comparação da eficácia da DFT e da FFT

A eficiência do algoritmo FFT e o número de operações realizadas linearmente dependem do comprimento da sequência N:


Como você pode ver, quanto maior a duração da conversão, maiores as economias em recursos de computação (em termos de velocidade de processamento ou número de unidades de hardware)!

Qualquer forma de onda arbitrária pode ser representada como um conjunto de sinais harmônicos de diferentes frequências. Em outras palavras, um sinal de forma complexa no domínio do tempo possui um conjunto de amostras complexas no domínio da frequência, denominadas * harmônicas *. Essas amostras expressam a amplitude e a fase do efeito harmônico em uma frequência específica. Quanto maior o conjunto de harmônicos no domínio da frequência, mais precisa é a forma de onda complexa.

Convolução e correlação

Esta seção apresenta o conceito de correlação e convolução para seqüências aleatórias e determinísticas discretas. A relação entre autocorrelação e funções de correlação cruzada com convolução é mostrada. As propriedades da convolução são descritas, em particular, são considerados os métodos de convolução linear e cíclica de um sinal discreto com análise detalhada no exemplo de uma sequência discreta. Além disso, é mostrado um método para calcular a convolução "rápida" usando algoritmos FFT.

Em problemas reais, a questão é frequentemente levantada sobre o grau de semelhança de um processo com outro ou sobre a independência de um processo em relação a outro. Em outras palavras, é necessário determinar a relação entre os sinais, ou seja, para encontrar uma correlação . Os métodos de correlação são usados ​​em uma ampla gama de tarefas: busca de sinais, visão computacional e processamento de imagens, em problemas de radar para determinar as características dos alvos e determinar a distância a um objeto. Além disso, a correlação é usada para procurar sinais fracos no ruído.

A convolução descreve a interação dos sinais entre si. Se um dos sinais é a resposta de impulso do filtro, a convolução da sequência de entrada com a resposta de impulso não passa de uma reação do circuito à ação de entrada. Em outras palavras, o sinal resultante reflete a passagem do sinal através do filtro.

A função de autocorrelação (ACF) é usada na informação de codificação. A escolha da sequência de codificação de acordo com os parâmetros de comprimento, frequência e forma é em grande parte devido às propriedades de correlação dessa sequência. A melhor sequência de código tem a menor probabilidade de detecção ou operação falsa (para detectar sinais, para dispositivos de limite) ou sincronização falsa (para transmitir e receber sequências de código).

Esta seção apresenta uma tabela comparando a eficácia da convolução rápida e da convolução calculada pela fórmula direta (pelo número de multiplicações reais).

Como você pode ver, para FFT de até 64, a convolução rápida perde para o método direto. No entanto, com um aumento no comprimento da FFT, os resultados mudam na direção oposta - uma convolução rápida começa a superar o método direto. Obviamente, quanto maior a FFT, melhor o ganho no método de frequência.

Sinais aleatórios e ruído

Nesta seção, é introduzido o conceito de sinais aleatórios, densidade de probabilidade e lei de distribuição aleatória. Momentos matemáticos são considerados - média (expectativa matemática) e variância (ou a raiz dessa quantidade é o desvio padrão). Também nesta seção, a distribuição normal e o conceito relacionado de ruído branco são considerados como a principal fonte de ruído (interferência) durante o processamento do sinal.

Um sinal aleatório é uma função do tempo cujos valores não são conhecidos antecipadamente e só podem ser previstos com alguma probabilidade . As principais características dos sinais aleatórios incluem:

• lei de distribuição (o tempo de permanência relativo do valor do sinal em um determinado intervalo),
• distribuição espectral da potência do sinal.

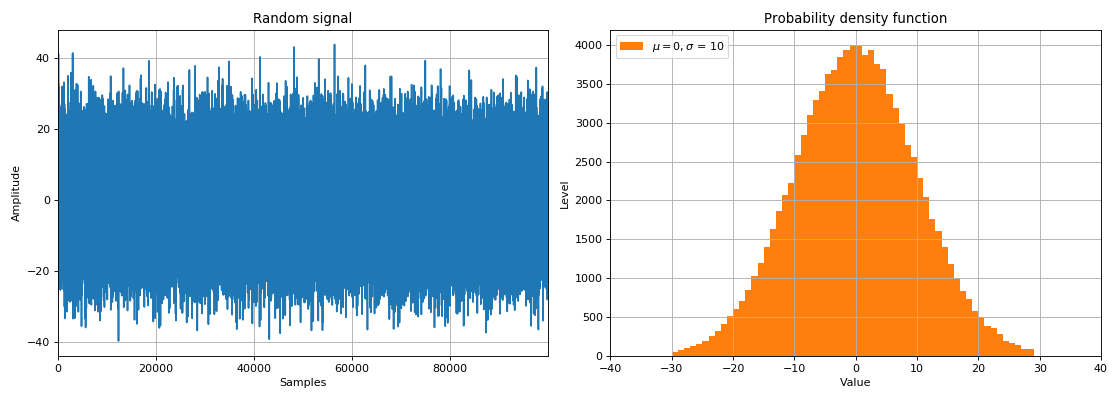
Nas tarefas DSP, os sinais aleatórios são divididos em duas classes:

• ruído - flutuações aleatórias constituídas por um conjunto de diferentes frequências e amplitudes,
• sinais que transportam informações, para cujo processamento é necessário recorrer a métodos probabilísticos.

Usando variáveis ​​aleatórias, podemos simular o efeito de um meio real na passagem de um sinal de uma fonte para um receptor de dados. Quando um sinal passa por algum link barulhento, o chamado ruído branco é adicionado ao sinal. Como regra, a densidade espectral de tal ruído é distribuída uniformemente (igualmente) em todas as frequências, e os valores de ruído no domínio do tempo são normalmente distribuídos (lei de distribuição gaussiana). Como o ruído branco é fisicamente adicionado às amplitudes do sinal nas amostras de tempo selecionadas, ele é chamado de ruído gaussiano aditivo branco (AWGN).

Sinais, Modulação e Manipulação

Esta seção mostra os métodos básicos para alterar um ou mais parâmetros de um sinal harmônico. Os conceitos de amplitude, frequência e modulação de fase são introduzidos. Em particular, a modulação linear de frequência usada em problemas de radar é destacada. As principais características dos sinais, os espectros dos sinais modulados, dependendo dos parâmetros de modulação são mostrados.



Por conveniência, um conjunto de funções foi criado no Python que implementa os tipos de modulação acima. Exemplo de implementação do sinal chirp:

 def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs): """ Create Chirp signal Parameters ---------- amp : float Signal magnitude beta : float Modulation bandwidth: beta < N for complex, beta < 0.5N for real freq : float or int Linear frequency of signal period : integer Number of points for signal (same as period) kwargs : bool Complex signal if is_complex = True Modulated by half-sine wave if is_modsine = True """ is_complex = kwargs.get('is_complex', False) is_modsine = kwargs.get('is_modsine', False) t = np.linspace(0, 1, period) tt = np.pi * (freq * t + beta * t ** 2) if is_complex is True: res = amp * (np.cos(tt) + 1j * np.sin(tt)) else: res = amp * np.cos(tt) if is_modsine is True: return res * np.sin(np.pi * t) return res 

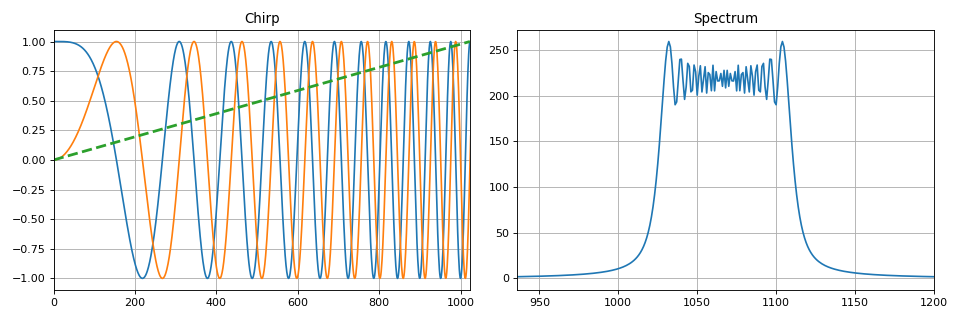
Também nesta seção da teoria da transmissão de mensagens discretas são descritos tipos de modulação digital - manipulações. Como no caso de sinais analógicos, as seqüências harmônicas digitais podem ser manipuladas em amplitude, fase e frequência (ou vários parâmetros ao mesmo tempo).

Filtros Digitais - IIR e FIR

Uma seção suficientemente grande dedicada à filtragem digital de sequências discretas. Nas tarefas de processamento de sinal digital, os dados fluem através de circuitos chamados filtros . Os filtros digitais, como os analógicos, têm características diferentes - frequência: resposta de frequência, resposta de fase, tempo: resposta de impulso, bem como a característica de transferência do filtro. Os filtros digitais são usados ​​principalmente para melhorar a qualidade do sinal - para isolar um sinal de uma sequência de dados ou para degradar sinais indesejados - para suprimir certos sinais nas seqüências de amostras recebidas.



A seção lista as principais vantagens e desvantagens dos filtros digitais (comparados aos analógicos). É introduzido o conceito de características de impulso e transferência do filtro. Duas classes de filtros são consideradas - com uma resposta de impulso infinito (IIR) e uma resposta de impulso finito (FIR). Um método para projetar filtros na forma canônica e direta é mostrado. Para filtros FIR, a questão de como alternar para um formato recursivo é considerada.



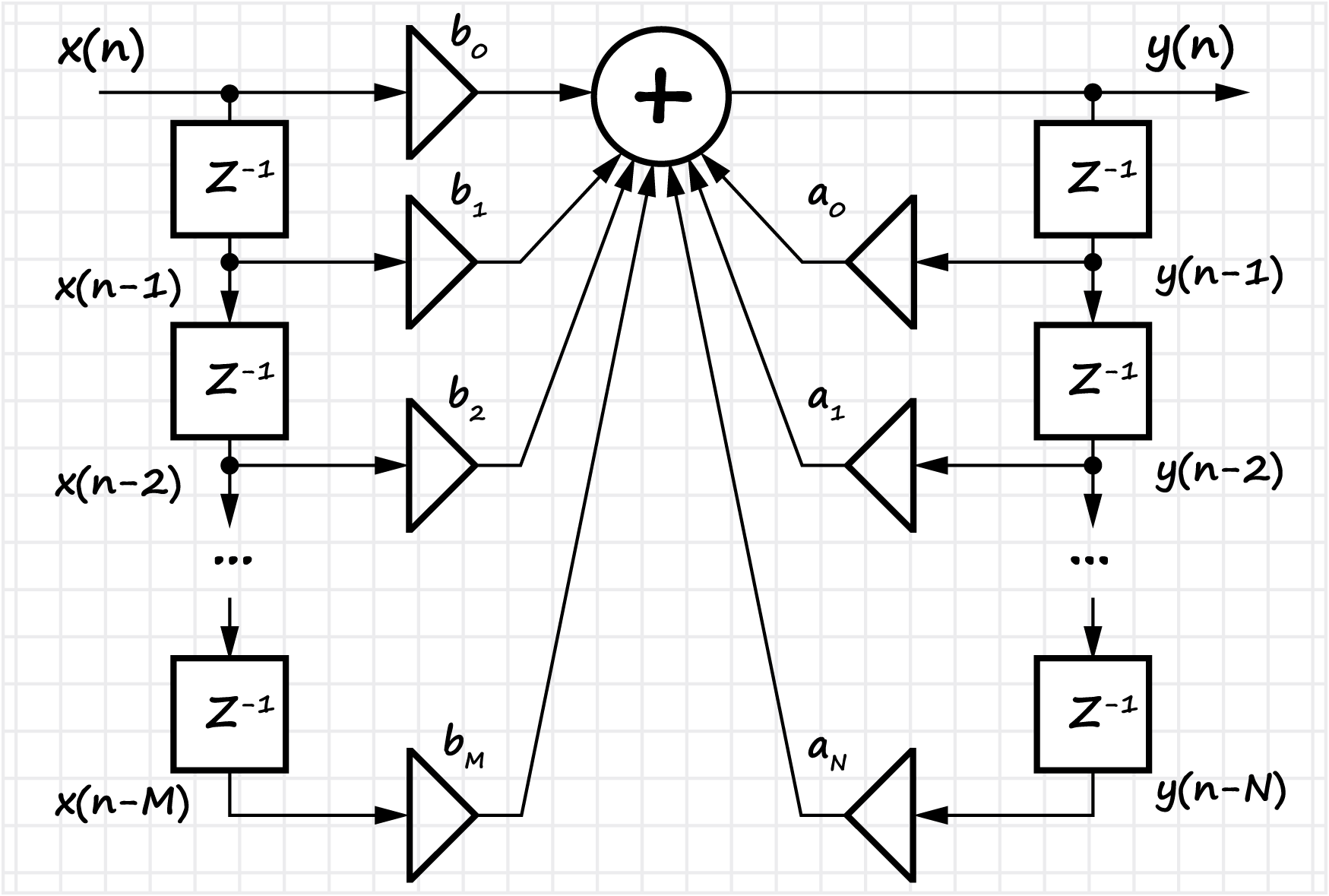
Para filtros FIR, o processo de design do filtro é mostrado desde o estágio de desenvolvimento das especificações técnicas (com os principais parâmetros indicados) até a implementação de software e hardware - procure coeficientes de filtro (levando em consideração a forma de representação do número, profundidade de bits etc.). São introduzidas as definições de filtros FIR simétricos, resposta de fase linear e sua relação com o conceito de atraso de grupo.

Funções de janela em tarefas de filtragem

Nas tarefas de processamento de sinal digital, são utilizadas funções de janela de várias formas, as quais, quando sobrepostas a um sinal no domínio do tempo, podem melhorar qualitativamente suas características espectrais. Um grande número de várias janelas se deve principalmente a um dos principais recursos de qualquer sobreposição de janela. Esse recurso é expresso na relação entre o nível dos lobos laterais e a largura do lobo central. Regra:

Quanto mais forte a supressão dos lobos laterais do espectro, maior o lóbulo principal do espectro e vice-versa.

Uma das aplicações das funções da janela: detecção de sinais fracos contra o fundo dos mais fortes, suprimindo o nível dos lobos laterais. As funções da janela principal nas tarefas DSP são: ** triangular, sinusoidal, Lanczos, Hann, Hamming, Blackman, Harris, janela Blackman-Harris, janela plana, Natall, Gauss, janela Kaiser ** e muitas outras. A maioria deles é expressa através de uma série finita pela soma de sinais harmônicos com pesos específicos. Tais sinais são perfeitamente implementados na prática em qualquer dispositivo de hardware (circuitos lógicos programáveis ​​ou processadores de sinais).

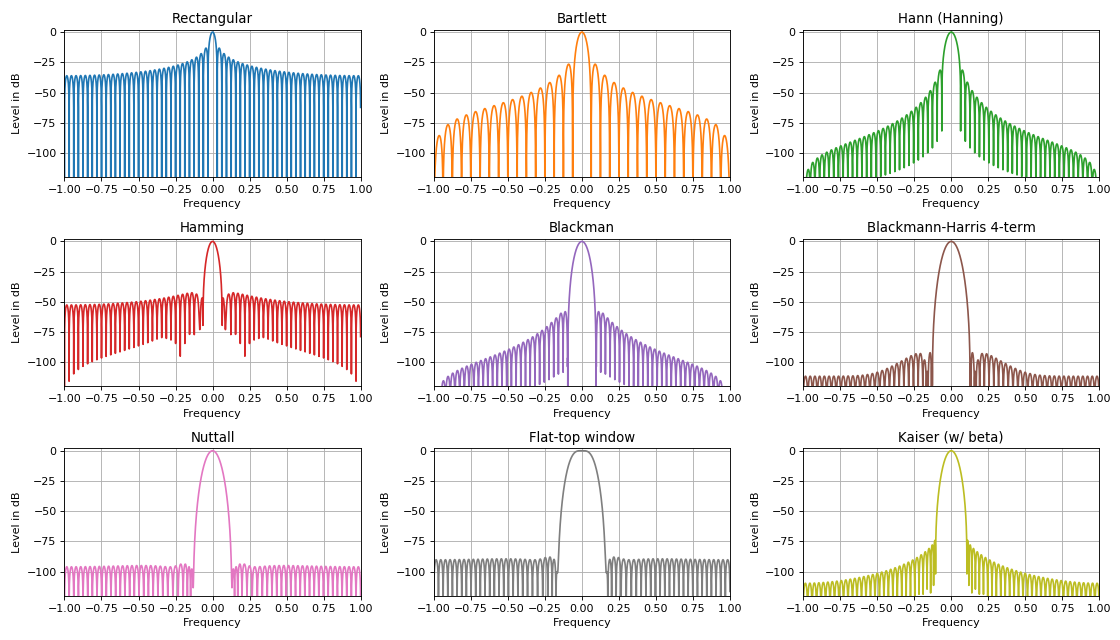
Reamostragem. Dizimação e interpolação

Esta seção discute os problemas do processamento de sinal em várias velocidades - alterações na frequência de amostragem. O processamento de sinais em várias velocidades (processamento em múltiplas taxas) sugere que, no processo de conversão linear de sinais digitais, é possível alterar a frequência de amostragem no sentido de diminuir ou aumentar, ou em um número fracionário de vezes. Isso leva a um processamento de sinal mais eficiente, pois abre a possibilidade de usar as frequências mínimas de amostragem permitidas e, como resultado, uma redução significativa no desempenho computacional necessário do sistema digital projetado.

Dizimação (dizimação) - downsampling. Interpolação - aumentando a taxa de amostragem.

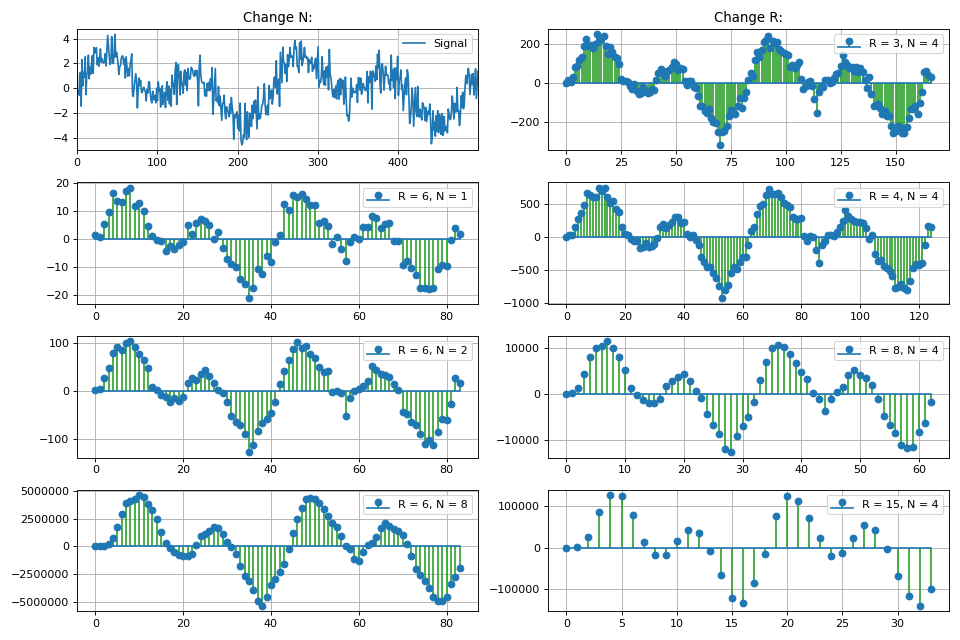
A seção também considera a classe de filtros FIR homogêneos, chamados de filtros de pente integral (CIC, integrador em cascata - pente). A implementação, propriedades básicas e recursos dos filtros CIC são mostrados. Devido à linearidade das operações matemáticas que ocorrem no filtro CIC, é possível cascatear vários filtros em sequência, o que proporciona uma diminuição proporcional no nível dos lobos laterais, mas também aumenta o "bloqueio" do lóbulo principal da característica de amplitude-frequência.



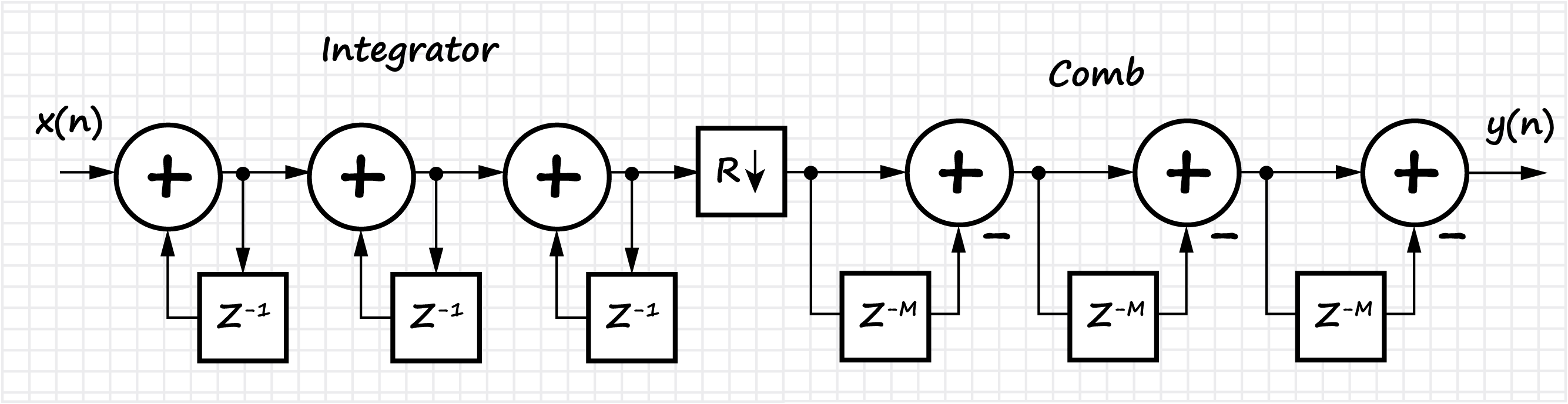
Gráfico da resposta em frequência do filtro, dependendo do coeficiente de dizimação:



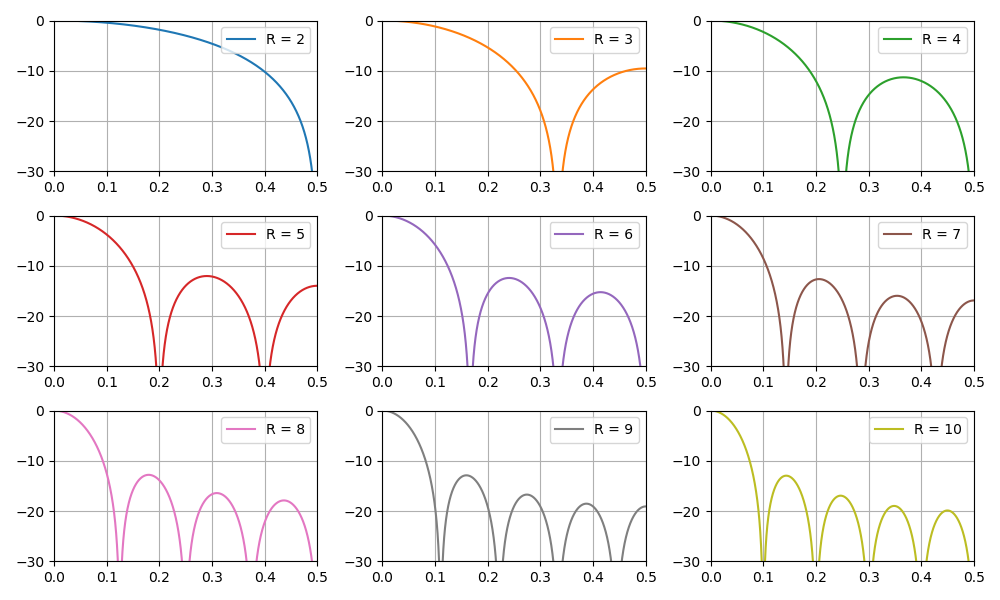
Também nesta seção, discutimos a questão de aumentar a profundidade de bits dos dados na saída do filtro CIC, dependendo de seus parâmetros. Isso é especialmente importante nas tarefas de implementação de software, principalmente nos FPGAs.

Para a implementação prática de filtros CIC em Python, uma classe separada CicFilter foi desenvolvida que implementa métodos de dizimação e interpolação. Também são mostradas alterações na taxa de amostra usando os métodos internos do pacote Python scipy.





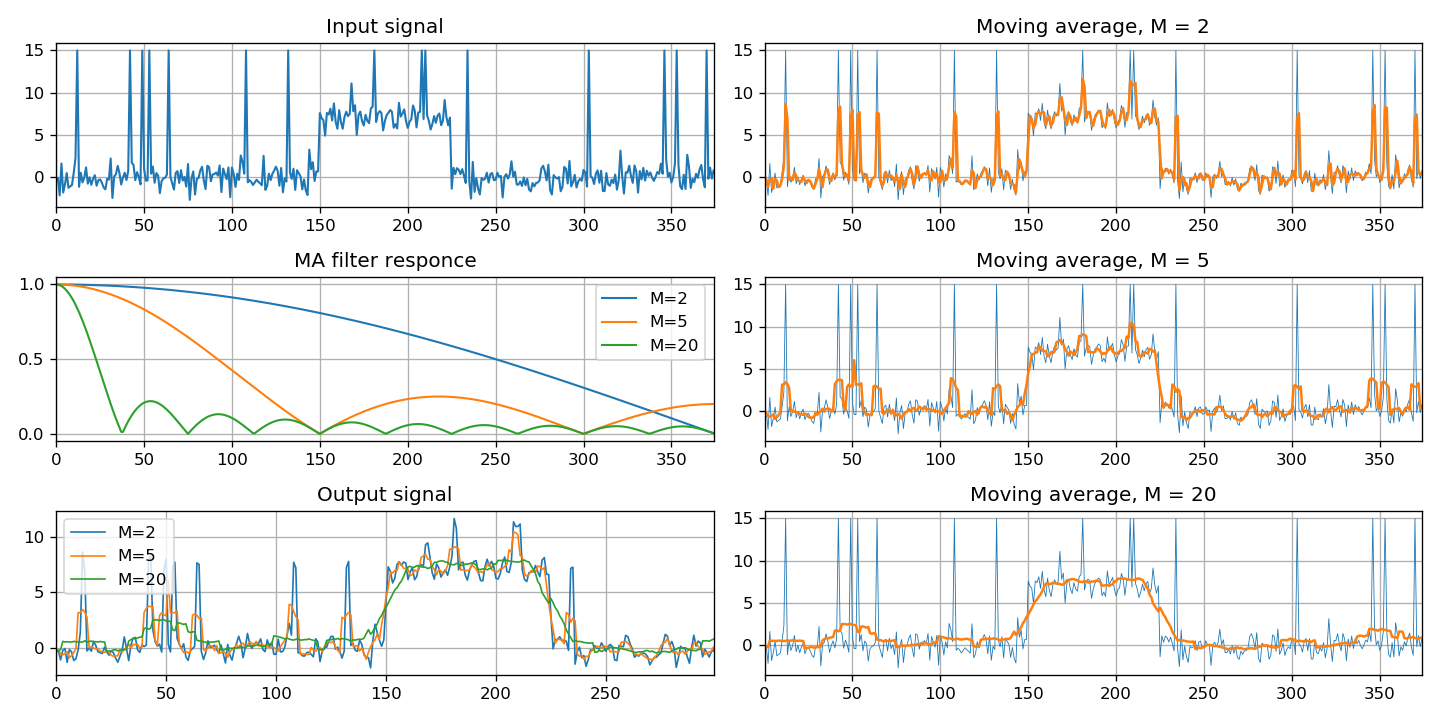
Por fim, esta seção fornece uma classe especial de filtros - a média móvel. Três métodos de implementação são mostrados: através da convolução de sinais, usando um filtro FIR e um filtro IIR.

Conclusão

Espero que este curso de palestras em conjunto com meus artigos anteriores sobre processamento digital de sinais FPGA traga benefícios práticos e ajude o leitor a entender melhor os conceitos básicos do processamento digital de sinais. Este projeto será aprimorado e complementado com novo material útil e não menos interessante. Siga o desenvolvimento!

Além deste material, apoio e desenvolvo meu projeto nos principais módulos DSP (em Python). Ele contém um pacote para gerar vários sinais, uma classe de filtros CIC para problemas de dizimação e interpolação, um algoritmo para calcular os coeficientes de um filtro FIR de correção, um filtro de média móvel, um algoritmo para calcular uma FFT ultra longa através de métodos de conversão bidimensional (este último foi muito útil ao trabalhar com implementação de hardware em FPGAs) .

Obrigado pela atenção!