Na escola, eu tinha um colega de classe que podia ouvir como o carro funciona no quintal e, com uma cara séria, faz um veredicto: tudo está em ordem, ou algo está quebrado, e eu preciso correr com urgência para novas peças / óleo / ferramentas! Eu, como um bule de chá absoluto no setor automotivo, sempre ouvia o barulho habitual do próximo dvenashka, sem perceber nenhuma diferença e apenas me maravilhando silenciosamente com sua audição e habilidades.
Agora eu não entendi melhor o interior do carro, mas comecei a trabalhar com o processamento de sinais sonoros e aprendizado de máquina, e aqui tentaremos entender se é possível ensinar um computador a detectar anormalidades no som de um motor?
No mínimo, é interessante verificar e, no futuro, essa tecnologia poderá economizar muito dinheiro para os proprietários de automóveis. Pelo menos na minha opinião, falhas críticas ocorrem gradualmente sob o capô e, nos estágios iniciais, muitas delas podem ser ouvidas, consertadas de forma rápida e barata, economizando tempo, dinheiro e nervos já instáveis.
Bem, talvez seja hora de passar de palavras para ações. Vamos lá!
Quero dizer imediatamente que em tudo que diz respeito a matemática e algoritmos, colocarei mais ênfase no significado e no entendimento, não haverá fórmulas e cálculos matemáticos aqui. Não desenvolvi nenhum novo algoritmo aqui; para fórmulas, se desejar, é melhor pesquisar no Google e na Wikipedia, além de usar os links que deixarei ao longo do artigo.
Vou dar todas as explicações sobre o exemplo do som de um mecanismo quebrado, retirado deste vídeo no YouTube .
O arquivo baixado do YouTube (você pode baixá-lo usando extensões do navegador ou simplesmente alterando o link do youtube para ssyoutube) convertemos para o formato wav usando ffmpeg:
ffmpeg -i input_video.mp4 -c:a pcm_s16le -ar 16000 -ac 1 engine_sound.wav
Antes de começar a processar este arquivo, vou dizer algumas palavras sobre o que é um espectrograma e como ele será útil para resolver esse problema. Muitos de vocês, com certeza, viram uma imagem semelhante - esta é a representação amplitude-temporal do som ou um oscilograma.
Se, em termos simples, o som é uma onda, e os valores de amplitude dessa onda são observados no oscilograma em determinados momentos.
Para obter um espectrograma de tal representação, precisamos da transformada de Fourier. Com sua ajuda, você pode obter a representação em amplitude-frequência do som ou o espectro de amplitude. Esse espectro mostra em que frequência e com que amplitude o sinal em estudo é expresso.
De fato, um espectrograma é um conjunto de espectros de pequenas partes consecutivas de um sinal. Talvez essa "definição" seja suficiente para não nos distrairmos muito da tarefa. Tudo ficará mais claro se você observar a visualização do espectrograma (a imagem foi obtida usando o WaveAssistant ). O tempo é plotado no eixo X, a frequência no eixo Y, ou seja, cada coluna nesta matriz é o módulo do espectro em um determinado ponto no tempo.
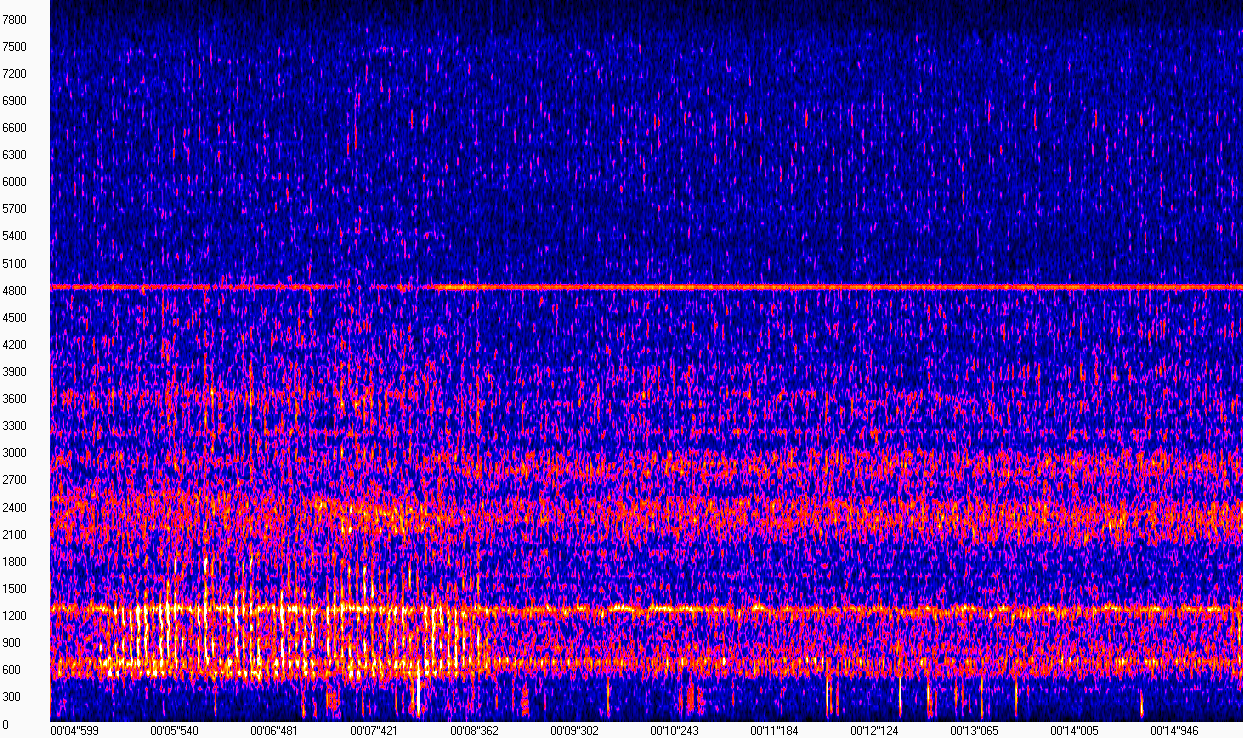
Este espectrograma mostra que o som do motor, na ausência de batidas, "parece" o mesmo e é expresso em frequências próximas a 600, 1200, 2400 e 4800 Hz. O som de uma batida que incomoda o proprietário é muito distinto na faixa de frequência de 600 a 1200 Hz de 5 a 8 segundos. Como a gravação foi feita em condições bastante barulhentas na rua, esses ruídos também estão presentes no espectrograma, o que complica um pouco a nossa tarefa.
No entanto, olhando para esse espectrograma, podemos dizer com segurança onde estava a batida e onde não estava. O computador não tem olhos, portanto, precisamos selecionar um algoritmo que seja capaz de distinguir entre esse desvio (e de preferência não apenas ele), sujeito à presença de ruído na gravação.
Os espectrogramas podem ser calculados usando a biblioteca librosa da seguinte maneira:
from librosa.util import buf_to_float from librosa.core import stft
Solução
A rigor, precisamos resolver o problema de classificação binária, onde precisamos determinar se o motor está com defeito ou se está funcionando normalmente. Meu colega e eu já descrevemos tarefas semelhantes em nosso artigo anterior , onde usamos uma rede neural convolucional para classificar eventos acústicos. Aqui, essa solução dificilmente é possível: os neurônios gostam muito quando recebem grandes conjuntos de dados. Estamos lidando com um único recuo que dura um pouco mais de um minuto, o que obviamente não pode ser chamado de um grande conjunto de dados.
A escolha foi interrompida no Modelo de Mistura Gaussiana (modelo de misturas Gaussianas). Um bom artigo detalhando o princípio de operação e treinamento deste modelo pode ser encontrado aqui.A idéia geral desse modelo é descrever os dados usando uma distribuição complexa na forma de uma combinação linear de várias distribuições normais multidimensionais (mais sobre a distribuição normal multidimensional aqui ).
Como o mecanismo durante sua operação soa aproximadamente “o mesmo”, o som de sua operação pode ser considerado estacionário, e a ideia de descrever esse som usando essa distribuição parece bastante significativa. Para entender a essência do GMM, eu recomendo olhar um exemplo de treinamento e escolher o número de gaussoids aqui .
Nosso caso difere dos exemplos acima, pois, em vez de pontos em um plano bidimensional, serão utilizados os valores do espectro retirados do espectrograma de sinal. Você pode selecionar parâmetros de distribuição, como o tipo de matriz de covariância, usando o critério BIC ( exemplo , descrição ); no entanto, no meu caso, os parâmetros ideais do ponto de vista desse critério mostraram-se piores do que aqueles mostrados no código abaixo:
from sklearn.mixture import GaussianMixture n_components = 3 gmm_clf = GaussianMixture(n_components) gmm_clf.fit(X_train)
Assumindo que o som da operação normal seja descrito por uma distribuição, cujos parâmetros foram selecionados durante o processo de treinamento, é possível medir a proximidade de qualquer som a essa distribuição.
Para fazer isso, você pode calcular a probabilidade média das colunas do espectrograma do sinal estudado e escolher um limite que separará a probabilidade de sons de bom trabalho de todos os outros. A credibilidade para cada segundo é a seguinte:
n_seconds = len(full_wav_data) // sr gmm_scores = []
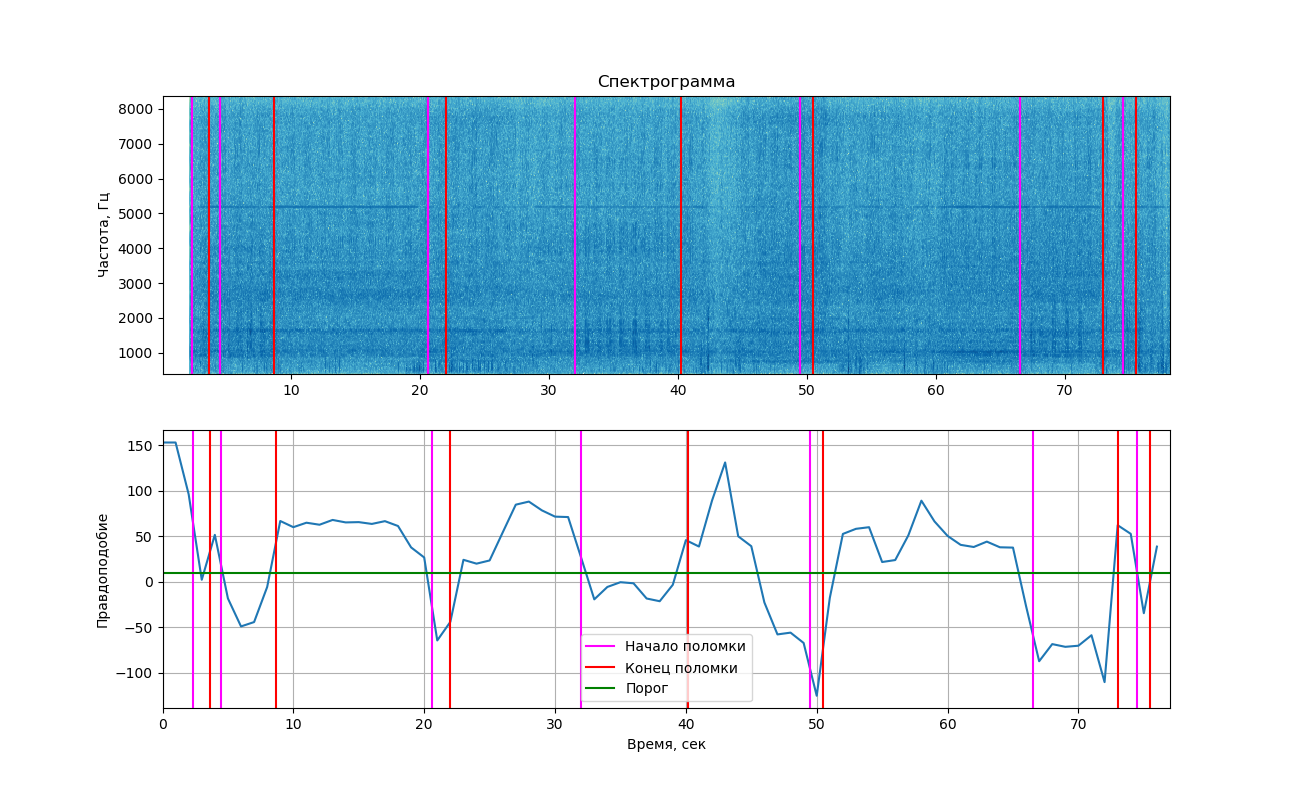
Se você exibir a probabilidade obtida no gráfico, obteremos a seguinte imagem.
A parte superior mostra o espectrograma do sinal exibido usando a biblioteca matplotlib. As alterações causadas por batidas não são visíveis tanto quanto no exemplo acima (e é por isso que você viu duas imagens aqui). No entanto, se você olhar de perto, eles ainda podem ser vistos. As linhas verticais marcam os horários de início e término da batida.
Conclusões
Como você pode ver no gráfico, no momento do som de uma batida, a probabilidade realmente caiu abaixo do limite, o que significa que poderíamos separar essas duas classes (trabalhando com e sem bater). Mas devo dizer que esse valor está próximo o suficiente do limiar e em áreas onde a batida não é ouvida. Isso ocorre porque ruídos estranhos são freqüentemente encontrados na gravação, o que também afeta a probabilidade.
Adicionamos aqui o treinamento em apenas alguns segundos de som, condições precárias de gravação, e você já pode se surpreender ao saber que o experimento foi de algum modo bem-sucedido!
Muito provavelmente, para aplicar esse método na prática e ter certeza de sua confiabilidade, você precisará gravar muito mais som e também colocar o microfone bem, a fim de minimizar o ruído que entra nas gravações.
Este artigo é apenas uma tentativa de resolver um problema semelhante, sem reivindicar correção absoluta, se você tiver idéias e sugestões, ou talvez perguntas, vamos discuti-las juntos nos comentários ou pessoalmente.
O código completo do github está aqui