A tradução do artigo foi preparada para os alunos do curso "Matemática para Ciência de Dados"

Anotação

Este artigo discute a tarefa de encontrar contornos faciais para uma única imagem. Mostramos como o conjunto de árvores de regressão pode ser usado para prever a posição dos contornos faciais diretamente de um subconjunto disperso de intensidades de pixels, obtendo super desempenho em tempo real com previsões de alta qualidade. Apresentamos uma estrutura geral baseada no aumento de gradiente para estudar um conjunto de árvores de regressão que otimiza a soma das perdas quadráticas e, naturalmente, processa dados ausentes ou parcialmente marcados. Mostraremos como o uso de distribuições apropriadas que levam em consideração a estrutura dos dados da imagem ajuda na seleção eficiente de contornos. Várias estratégias de regularização e sua importância na luta contra a reciclagem também estão sendo investigadas. Além disso, analisamos o efeito da quantidade de dados de treinamento na precisão das previsões e examinamos o efeito de aumentar os dados usando dados sintetizados.

1. Introdução

Neste artigo, apresentamos um novo algoritmo que procura contornos faciais em milissegundos e obtém uma precisão superior ou comparável aos métodos modernos em conjuntos de dados padrão. O aumento da velocidade em comparação aos métodos anteriores é uma consequência da identificação dos principais componentes dos algoritmos anteriores para a busca de contornos faciais e sua subsequente inclusão de forma otimizada na cascata de modelos de regressão com alta largura de banda, sintonizados com o aumento de gradiente.

Demonstramos, como já fizemos antes [8, 2], que a busca por contornos faciais pode ser realizada usando uma cascata de modelos de regressão. No nosso caso, cada modelo de regressão em cascata prediz efetivamente o formato da face com base na previsão inicial e a intensidade do conjunto esparso de pixels indexados em relação a essa previsão inicial. Nosso trabalho se baseia em um grande número de estudos realizados na última década, que levaram a um progresso significativo na tarefa de encontrar contornos faciais [9, 4, 13, 7, 15, 1, 16, 18, 3, 6, 19]. Em particular, incluímos em nossos modelos de regressão sintonizados dois elementos-chave presentes em vários algoritmos bem-sucedidos abaixo, e agora estamos detalhando esses elementos.

Figura 1. Resultados selecionados no conjunto de dados HELEN. Para detectar 194 pontos-chave (pontos de referência) na face em uma imagem em um milissegundo, é utilizado um conjunto de árvores de regressão aleatória.

O primeiro gira em torno da indexação da intensidade de pixel em relação à previsão atual do formato da face. Os recursos distintos na representação vetorial da imagem da face podem variar bastante devido à deformação da forma e devido a fatores interferentes como alterações nas condições de iluminação. Isso dificulta a previsão precisa da forma usando essas funções. O dilema é que precisamos de sinais confiáveis ​​para prever com precisão a forma e, por outro lado, precisamos de uma previsão precisa da forma para extrair sinais confiáveis. No trabalho anterior [4, 9, 5, 8], bem como neste trabalho, uma abordagem iterativa (cascata) é usada para resolver esse problema. Em vez de regredir os parâmetros de forma com base nos recursos extraídos no sistema de coordenadas da imagem global, a imagem é convertida em um sistema de coordenadas normalizado com base na previsão de forma atual e, em seguida, são extraídos sinais para prever o vetor de atualização dos parâmetros de forma. Esse processo geralmente é repetido várias vezes até a convergência.

O segundo examina como lidar com a complexidade do problema de explicação / previsão. Durante o teste, o algoritmo de busca de contorno deve prever o formato da face - um vetor de alta dimensão que está em melhor concordância com os dados da imagem e nosso modelo de formato. O problema é não-convexo com muitas ótimas locais. Algoritmos de sucesso [4, 9] resolvem esse problema, assumindo que a forma prevista deve estar em um subespaço linear que pode ser detectado, por exemplo, encontrando os principais componentes das formas de treinamento. Essa suposição reduz significativamente o número de possíveis formulários considerados durante a explicação e pode ajudar a evitar ótimos locais.

Um trabalho recente [8, 11, 2] explora o fato de que certa classe de regressores é garantida para criar previsões que se encontram no subespaço linear definido pelas formas de aprendizado, e não há necessidade de restrições adicionais. É importante que nossos modelos de regressão tenham esses dois elementos.
Esses dois fatores estão associados ao nosso treinamento efetivo no modelo de regressão. Otimizamos a função de perda correspondente e executamos a seleção de recursos com base nos dados. Em particular, treinamos cada regressor usando o aumento de gradiente [10] usando a função de perda quadrática, a mesma função de perda que queremos minimizar durante o teste. O conjunto de pixels esparsos usados ​​como entrada para o regressor é selecionado usando uma combinação do algoritmo de aumento de gradiente e a probabilidade a priori das distâncias entre pares de pixels de entrada. Uma distribuição a priori permite que o algoritmo de reforço investigue eficientemente um grande número de recursos relevantes. O resultado é uma cascata de regressores que podem localizar pontos de referência faciais quando inicializados de frente.

As principais contribuições deste artigo são:

1. Um novo método para encontrar contornos faciais, com base em um conjunto de árvores de regressão (árvores de decisão), que executa a seleção de recursos invariantes do formulário, minimizando a mesma função de perda durante o treinamento que queremos minimizar durante o teste.
2. Apresentamos uma extensão natural do nosso método que processa rótulos ausentes ou indefinidos.
3. São apresentados resultados quantitativos e qualitativos, que confirmam que nosso método fornece previsões de alta qualidade, sendo muito mais eficazes que o melhor método anterior (Figura 1).
4. É analisada a influência da quantidade de dados de treinamento, o uso de dados parcialmente rotulados e dados generalizados na qualidade das previsões.

2. Método

Este artigo apresenta um algoritmo para avaliar com precisão a posição dos pontos de referência faciais (pontos-chave) em termos de eficiência computacional. Como em trabalhos anteriores [8, 2], a cascata de regressores é usada em nosso método. No restante desta seção, descrevemos os detalhes da forma dos componentes individuais da cascata e como conduzimos o treinamento.

2.1 Cascata de regressão

Primeiro, introduzimos alguma notação. Vamos , coordenadas y do i-ésimo marco da face na imagem I. Em seguida, o vetor denota as coordenadas de todas as faces p em I. Muitas vezes, neste artigo, chamamos o vetor S de forma. Nós usamos para indicar nossa classificação atual S. Cada regressor (·, ·) Na cascata prevê o vetor de atualização da imagem e que é adicionado à avaliação do formulário atual Para melhorar a classificação:

) (1)

O ponto chave da cascata é que o regressor faz suas previsões com base em atributos como intensidades de pixel calculados por I e indexados em relação à estimativa de forma atual . Isso introduz algum tipo de invariância geométrica no processo e, à medida que você avança na cascata, pode ter mais certeza de que a localização semântica exata na face é indexada. Mais adiante, descreveremos como essa indexação é realizada.

Observe que a faixa de saída estendida pelo conjunto está garantida no subespaço linear dos dados de treinamento se a estimativa inicial pertence a este espaço. Portanto, não precisamos introduzir restrições adicionais nas previsões, o que simplifica bastante nosso método. O formulário inicial pode ser simplesmente selecionado como o meio dos dados de treinamento, centralizado e dimensionado de acordo com a saída da caixa delimitadora do detector de faces geral.

Educar a todos usamos o algoritmo de aumento de gradiente para árvores com a soma das perdas quadráticas, conforme descrito em [10]. Agora, forneceremos detalhes detalhados desse processo.

2.2 Treinando cada regressor em cascata

Suponha que tenhamos dados de treinamento onde todo mundo é uma imagem de rosto e seu vetor de forma. Para descobrir a primeira função de regressão na cascata, criamos a partir de nossos trigêmeos de dados de treinamento da imagem da face, a previsão inicial da forma e a etapa de atualização da meta, ou seja, ) onde

2)

(3) e

4)

para i = 1, ..., N.

Definimos o número total desses trigêmeos como N = nR, onde R é o número de inicializações usadas na imagem Ii. Cada previsão inicial de forma para a imagem é selecionada igualmente sem substituição.

Com esses dados, treinamos a função de regressão (veja Algoritmo 1) usando o aumento gradiente de árvores com a soma das perdas quadráticas. O conjunto de trigêmeos de treinamento é atualizado para fornecer dados de treinamento. % 20) para o próximo regressor na cascata, definindo (com t = 0).

% 20) (5)

(6)

Esse processo é repetido até que uma cascata de regressores T seja treinada. que em combinação fornecem um nível suficiente de precisão.

Conforme indicado, cada regressor aprende usando o algoritmo de aumento de árvore de gradiente. Deve-se lembrar que a função de perda quadrática é usada e os resíduos calculados no loop interno correspondem ao gradiente dessa função de perda estimada em cada amostra de treinamento. A formulação do algoritmo inclui o parâmetro de taxa de aprendizado 0 <ν ≤ 1, também conhecido como coeficiente de regularização. Definir ν <1 ajuda a combater a reconfiguração e geralmente leva a regressores que generalizam muito melhor do que aqueles treinados com ν = 1 [10].

Algoritmo de Aprendizagem 1 em cascata

Temos dados de treinamento e taxa de aprendizagem (coeficiente de regularização) 0 <ν <1

1. Inicializar
   
2. para k = 1, ..., K:
   a) definimos para i = 1, ...,
   
   b) Ajustamos a árvore de regressão ao alvo com função de regressão fraca .
   c) Atualização
3. Conclusão
   

2.3 Regressor em árvore

No centro de cada função de regressão rt estão os regressores do tipo árvore, adequados para alvos residuais durante o algoritmo de aumento de gradiente. Agora, examinaremos os detalhes de implementação mais importantes para o treinamento de cada árvore de regressão.

2.3.1 Testes invariáveis ​​de formulários divididos

Em cada nó de separação na árvore de regressão, tomamos uma decisão com base no valor limite da diferença entre as intensidades de dois pixels. Os pixels usados ​​no teste estão nas posições u e v quando são definidos no sistema de coordenadas da forma intermediária. Para uma imagem de uma face com uma forma arbitrária, gostaríamos de indexar pontos que tenham a mesma posição em relação à sua forma que u e v, para a forma média. Para fazer isso, antes de extrair os elementos, a imagem pode ser deformada na forma do meio, com base na estimativa da forma atual. Como usamos apenas uma representação muito esparsa da imagem, é muito mais eficiente deformar o arranjo de pontos do que toda a imagem. Além disso, uma aproximação aproximada da deformação pode ser feita usando apenas a transformação de similaridade global, além dos deslocamentos locais, conforme proposto em [2].

Os detalhes exatos são os seguintes. Vamos O índice do ponto de referência na face, na forma do meio, é o mais próximo de u e define seu deslocamento de u como .

Em seguida, para o formulário Si definido na imagem posição em , que é qualitativamente semelhante a u na imagem de forma média, é definido como
(7)

onde e - matriz de escala e rotação da transformada de similaridade que transforma em , forma do meio.

Escala e rotação minimizam

(8)

a soma dos quadrados entre os pontos de referência da forma do meio, e apontar urdidura. definido da mesma forma.

Formalmente, cada divisão é uma solução que inclui 3 parâmetros θ = (τ, u, v) e é aplicada a cada exemplo de treinamento e teste como

(9)

onde e são determinados usando a matriz de escala e rotação que melhor deforma em de acordo com a equação (7). Na prática, tarefas e deslocamentos locais são determinados na fase de treinamento. O cálculo da transformação de similaridade, durante o teste da parte mais cara desse processo, é realizado apenas uma vez em cada nível da cascata.

2.3.2 Seleção de partições nodais

Para cada árvore de regressão, aproximamos a função básica por uma função linear por partes, onde um vetor constante é adequado para cada nó finito. Para treinar a árvore de regressão, geramos aleatoriamente um conjunto de partições adequadas, ou seja, θ, em cada nó. Em seguida, selecionamos ansiosamente θ * desses candidatos, o que minimiza a soma do erro quadrático. Se Q é um conjunto de índices de exemplos de treinamento em um nó, isso corresponde à minimização

(10)

onde - índices de exemplos que são enviados para o nó esquerdo devido à decisão θ, É o vetor de todos os resíduos calculados para a imagem i no algoritmo de aumento de gradiente e

para (11)

A partição ideal pode ser encontrada com muita eficiência, porque se transformarmos a equação (10) e omitir fatores independentes de θ, podemos ver que

Aqui só precisamos calcular ao avaliar vários θ's, já que pode ser calculado a partir das metas médias no nó pai µ e da seguinte maneira:

2.3.3 Seleção de características

A solução em cada nó é baseada em um valor limite da diferença nos valores de intensidade em um par de pixels. Este é um teste bastante simples, mas é muito mais eficaz que um valor limite com uma única intensidade, devido à sua insensibilidade relativa às mudanças na iluminação global. Infelizmente, a desvantagem do uso de diferenças de pixel é que o número de possíveis candidatos à separação (recurso) é quadrático em relação ao número de pixels na imagem média. Isso torna difícil encontrar bons θ sem procurar um número muito grande deles. No entanto, esse fator limitante pode ser um pouco enfraquecido, levando em consideração a estrutura dos dados da imagem.

Introduzimos a distribuição exponencial

(12)

pela distância entre os pixels usados ​​na divisão para incentivar a seleção de pares mais próximos de pixels.

Descobrimos que o uso dessa distribuição simples reduz o erro de previsão para vários conjuntos de dados de face. A Figura 4 compara os recursos selecionados com e sem ele, em que o tamanho do conjunto de objetos nos dois casos é definido como 20.

2.4 Manipulação de tags ausentes

O problema da equação (10) pode ser facilmente estendido para lidar com o caso quando alguns pontos de referência não são marcados em algumas imagens de treinamento (ou temos uma medida de incerteza para cada ponto de referência). Inserir variável [0, 1] para cada imagem de treinamento ie cada marco j . Instalação um valor 0 indica que o marco j não está marcado na i- ésima imagem e uma configuração 1 indica que está marcado. Então a equação (10) pode ser representada da seguinte forma

onde - matriz diagonal com vetor na diagonal e

para (13)

O algoritmo de aumento de gradiente também deve ser modificado para levar em consideração esses pesos. Isso pode ser feito simplesmente inicializando o modelo de conjunto com o valor médio ponderado dos alvos e ajustando as árvores de regressão aos resíduos ponderados no algoritmo 1 da seguinte maneira

(14)

3. Experiências

Bases: para avaliar com precisão o desempenho do nosso método proposto, conjunto de árvores de regressão (ERT), criamos mais duas bases. O primeiro é baseado em samambaias aleatórias (samambaias aleatórias) com uma seleção aleatória de características (EF), e a outra é uma versão mais avançada dessa abordagem com a seleção de características baseadas na correlação (EF + CB), que é a nossa nova implementação [2]. Todos os parâmetros são fixos para as três abordagens.

A EF usa a implementação direta de samambaias aleatórias como regressores fracos no conjunto e é a mais rápida para o treinamento. Utilizamos o mesmo método de regularização sugerido em [2] para regularização de samambaias.

O EF + CB usa um método de seleção de objetos baseado em correlação que projeta valores de saída, , para uma direção aleatória we seleciona pares de sinais (u, v) para os quais tem a maior correlação de amostra para dados de treinamento com metas previstas .

Parâmetros
Salvo indicação em contrário, todas as experiências são realizadas com as seguintes configurações de parâmetros fixos. O número de regressores fortes rt na cascata é T = 10, e cada consiste em K = 500 regressores fracos . Profundidade das árvores (ou samambaias) usadas para representar , defina igual a F = 5. Em cada nível da cascata, P = 400 pixels são selecionados na imagem. Para treinar regressores fracos, selecionamos aleatoriamente um par desses pixels P de acordo com nossa distribuição e selecionamos um limite aleatório para criar uma separação de potencial, conforme descrito na equação (9). A melhor separação é obtida repetindo esse processo S = 20 vezes e escolhendo aquele que otimiza nosso objetivo. , R = 20 .

2. , Viola & Jones [17]. .

O (TKF). O (NDTKF S), N — , D — . HELEN [12], .

, , HELEN [12], , , . 2330 , 194 . 2000 , .

LFPW [1], 1432 . , 778 216 , , .

Comparação
1 . (Active Shape Models) — STASM [14] CompASM [12].

1. HELEN. — . . , . , . .

, , . 3 , , ERT , . , EF + CB . , EF + CB , .

LFPW [1] ( 2). EF + CB , [2]. ( , .) , , .

2. LFPW. 1.

4 (12) , , . λ 0,1 . . 4 .

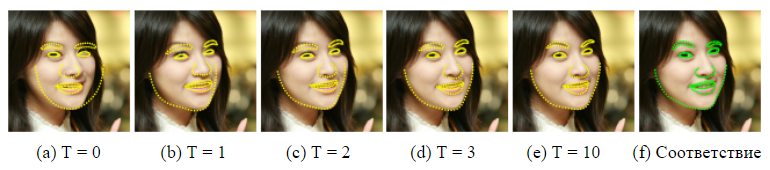
3. . , , . (12).

, . , . — . ν 1 ( ν = 0.1). . , , , ν = 1. (10 ) . ( .)

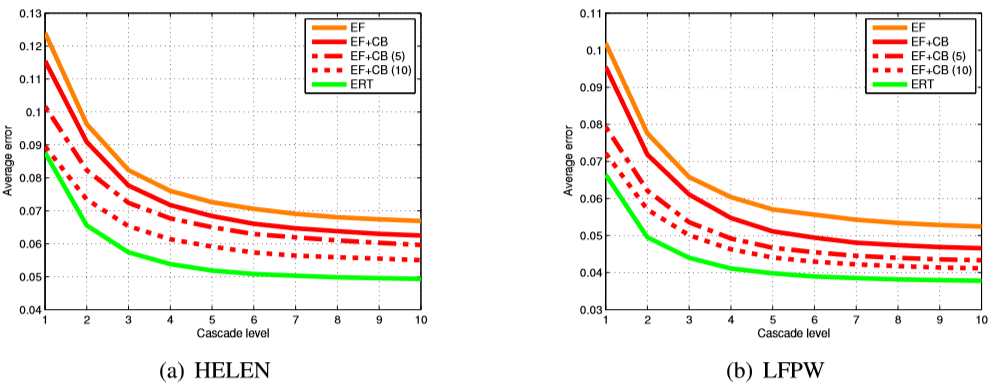
3. HELEN (a) LFPW (b). EF — , EF + CB — , . (5 10), [2]. , (ERT), , , .

4. , . , .

, . , .

4. HELEN . .

, . , , , , .

. . 5 . , , [8, 2] ( 10 × 400 .)

5. .

Dados de treinamento
Para testar a eficácia de nosso método em termos de número de imagens de treinamento, treinamos vários modelos de diferentes subconjuntos de dados de treinamento. A Tabela 6 resume os resultados finais e a Figura 5 mostra um gráfico de erros em cada nível da cascata. Usar muitos níveis de regressores é mais útil quando temos um grande número de exemplos de treinamento.

Repetimos as mesmas experiências com um número total fixo de exemplos estendidos, mas alteramos a combinação dos formulários iniciais usados ​​para criar o exemplo de treinamento a partir de um exemplo marcado da face e de um número de imagens anotadas usadas para estudar a cascata (Tabela 7).

Tabela 6. A taxa de erro final para o número de exemplos de treinamento. Ao criar dados de treinamento para o estudo de regressores em cascata, cada imagem de face etiquetada gerou 20 exemplos de treinamento, usando 20 faces etiquetadas diferentes como uma suposição inicial sobre o formato da face.

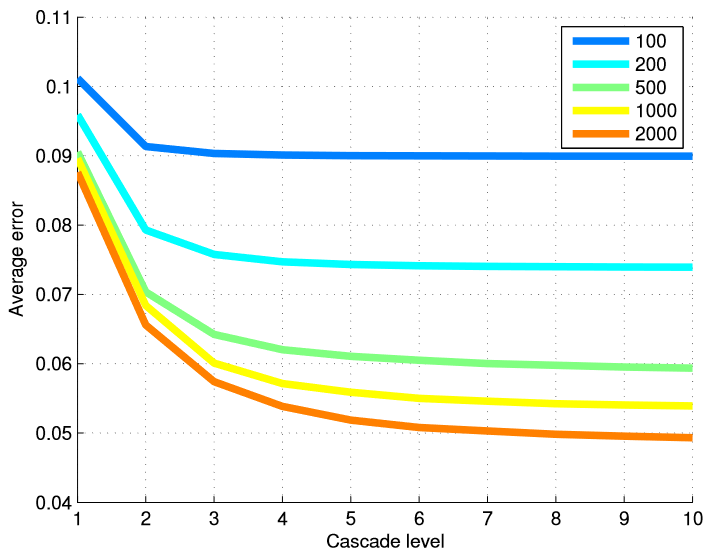
Figura 5. O erro médio em cada nível da cascata é apresentado dependendo do número de exemplos de treinamento usados. O uso de muitos níveis de regressores é mais útil quando o número de exemplos de treinamento é grande.

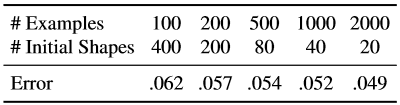
Tabela 7. Aqui, o número efetivo de exemplos de treinamento é fixo, mas usamos várias combinações do número de imagens de treinamento e o número de formulários iniciais usados ​​para cada imagem de rosto marcada.

Aumentar os dados de treinamento usando uma variedade de formulários iniciais expande o conjunto de dados em termos de formulário. Nossos resultados mostram que esse tipo de suplemento não compensa completamente a ausência de imagens de treinamento anotadas. Embora a taxa de melhoria obtida pelo aumento do número de imagens de treinamento esteja diminuindo rapidamente após as primeiras centenas de imagens.

Anotações parciais
A Tabela 8 mostra os resultados do uso de dados parcialmente anotados. 200 estudos de caso são anotados completamente, e o restante apenas parcialmente.

Tabela 8. Resultados usando dados parcialmente rotulados. 200 exemplos são sempre completamente anotados. Os valores entre parênteses indicam a porcentagem de pontos de referência observados.

Os resultados mostram que podemos obter melhorias significativas usando dados parcialmente rotulados. No entanto, a melhoria exibida pode não estar saturada, porque sabemos que o tamanho da base dos parâmetros de forma é muito menor que o tamanho dos pontos de referência (194 × 2). Conseqüentemente, existe o potencial de melhorias mais significativas com marcas parciais, se você usar explicitamente a correlação entre a posição dos pontos de referência. Observe que o procedimento de aumento de gradiente descrito neste artigo não usa correlação entre pontos de referência. Esse problema pode ser resolvido em trabalhos futuros.

4. Conclusão

Descrevemos como um conjunto de árvores de regressão pode ser usado para regredir a localização dos pontos de referência faciais a partir de um subconjunto disperso de valores de intensidade extraídos da imagem de entrada. A estrutura apresentada reduz o erro mais rapidamente do que o trabalho anterior e também pode processar marcas parciais ou indefinidas. Embora os principais componentes de nosso algoritmo considerem várias medidas de destino como variáveis ​​independentes, a continuação natural deste trabalho será o uso da correlação de parâmetros de forma para um treinamento mais eficaz e melhor uso de rótulos parciais.

Figura 6. Resultados finais no banco de dados HELEN.

Agradecimentos
Este trabalho foi financiado pela Swedish Strategic Research Foundation como parte do projeto VINST.

Literatura usada

[1] PN Belhumeur, DW Jacobs, DJ Kriegman e N. Kumar. Localizando partes das faces usando um consenso de exemplos. No CVPR, páginas 545–552, 2011. 1, 5
[2] X. Cao, Y. Wei, F. Wen e J. Sun. Alinhamento da face por regressão explícita da forma. No CVPR, páginas 2887–2894, 2012. 1, 2, 3, 4, 5, 6
[3] TF Cootes, M. Ionita, C. Lindner e P. Sauer. Ajuste de modelo de forma robusto e preciso usando votação por regressão aleatória da floresta. No ECCV, 2012.1
[4] TF Cootes, CJ Taylor, DH Cooper e J. Graham. Modelos de formas ativas - seu treinamento e aplicação. Computer Vision and Image Understanding, 61 (1): 38–59, 1995.1, 2
[5] D. Cristinacce e TF Cootes. Modelos de forma ativa de regressão reforçada. Na BMVC, páginas 79.1–79.10, 2007.1
[6] M. Dantone, J. Gall, G. Fanelli e LV Gool. Detecção de recursos faciais em tempo real usando florestas de regressão condicional. No CVPR, 2012.1
[7] L. Ding e AM Martínez. Detecção precisa e precisa de rostos e características faciais. No CVPR, 2008.1
[8] P. Dollar, P. Welinder e P. Perona. Regressão em pose em cascata. No CVPR, páginas 1078-1085, 2010. 1, 2, 6
[9] GJ Edwards, TF Cootes e CJ Taylor. Avanços nos modelos de aparência ativa. No ICCV, páginas 137-142, 1999. 1, 2
[10] T. Hastie, R. Tibshirani e JH Friedman. Os elementos do aprendizado estatístico: mineração de dados, inferência e previsão. Nova York: Springer-Verlag, 2001.2,3
[11] V. Kazemi e J. Sullivan. Alinhamento da face com modelagem baseada em peças. Na BMVC, páginas 27.1–27.10, 2011.2
[12] V. Le, J. Brandt, Z. Lin, LD Bourdev e TS Huang. Localização interativa de recursos faciais. Em [13] L. Liang, R. Xiao, F. Wen e J. Sun. Alinhamento de rosto por meio de pesquisa discriminativa baseada em componentes. No ECCV, páginas 72–85, 2008. 1ECCV, páginas 679– 692, 2012.5
[14] S. Milborrow e F. Nicolls. Localizando recursos faciais com um modelo de formato ativo estendido. No ECCV, páginas 504-513, 2008.5
[15] J. Saragih, S. Lucey e J. Cohn. Ajuste de modelo deformável por meio de marcações regulares de referência. International Journal of Computer Vision, 91: 200–215, 2010.1
[16] BM Smith e L. Zhang. Alinhamento de face de junta com modelos de formato não paramétricos. No ECCV, páginas 43–56, 2012.1
[17] PA Viola e MJ Jones. Detecção de rosto robusta em tempo real. No ICCV, página 747, 2001.5
[18] X. Zhao, X. Chai e S. Shan. Alinhamento da face da junta: Resgate alinhamentos ruins com os bons, mediante reajustamento regular. No ECCV, 2012.1
[19] X. Zhu e D. Ramanan. Detecção de rosto, estimativa de pose e localização de marcos na natureza. No CVPR, páginas 2879–2886, 2012.1