Por que o próximo artigo sobre como escrever redes neurais do zero? Infelizmente, não consegui encontrar artigos em que a teoria e o código fossem descritos do zero para um modelo totalmente funcional. Eu imediatamente aviso que haverá muita matemática. Suponho que o leitor esteja familiarizado com os conceitos básicos de álgebra linear, derivadas parciais e, pelo menos parcialmente, com a teoria das probabilidades, além de Python e Numpy. Lidaremos com uma rede neural totalmente conectada e com o MNIST.
Matemática Parte 1 (simples)
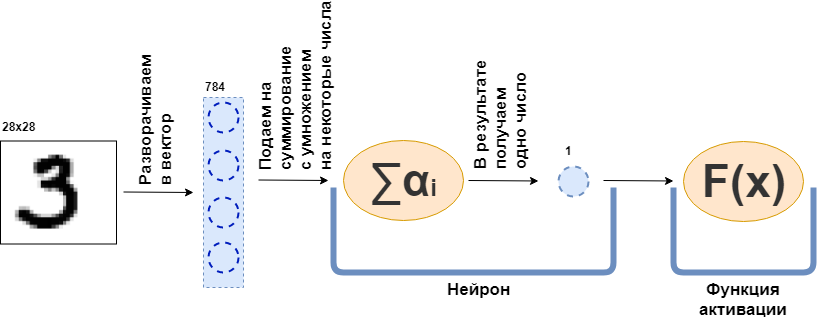
O que é uma camada totalmente conectada (camada FC)? Geralmente eles dizem algo como "Uma camada totalmente conectada é uma camada, cada neurônio conectado a todos os neurônios da camada anterior". Não está claro o que são os neurônios, como eles estão conectados, especialmente no código. Agora vou tentar analisar isso com um exemplo. Que haja uma camada de 100 neurônios. Eu sei que ainda não expliquei o que é, mas vamos imaginar que existem 100 neurônios e eles têm uma entrada para onde os dados são enviados e uma saída de onde eles fornecem os dados. E uma imagem em preto e branco de 28x28 pixels é alimentada na entrada - apenas 784 valores, se você a esticar em um vetor. Uma imagem pode ser chamada de camada de entrada. Então, para que cada um dos 100 neurônios se conecte a cada "neurônio" ou, se quiser, o valor da camada anterior (ou seja, a figura), é necessário que cada um dos 100 neurônios aceite 784 valores da figura original. Por exemplo, para cada um dos 100 neurônios, basta multiplicar 784 valores da imagem por cerca de 784 números e adicioná-los, como resultado, um número sai. Ou seja, este é um neurônio:
$$ display $$ \ text {Saída do neurônio} = \ text {algum número} _ {1} \ cdot \ text {valor da imagem} _1 ~ + \\ + ~ ... ~ + ~ \ text {some- esse número} _ {784} \ cdot \ text {valor da imagem} _ {784} $$ display $$
Acontece que cada neurônio tem 784 números e todos esses números: (número de neurônios nessa camada) x (número de neurônios na camada anterior) =
$ inline $ 100 \ times784 $ inline $ = 78.400 dígitos. Esses números são comumente chamados de pesos da camada. Cada neurônio fornecerá seu número e, como resultado, obteremos um vetor 100-dimensional e, de fato, podemos escrever que esse vetor 100-dimensional é obtido multiplicando o vetor 784-dimensional (nossa imagem original) por uma matriz de peso do tamanho
$ inline $ 100 \ times784 $ inline $ :
exibição $$ $$ \ boldsymbol {x} ^ {100} = W_ {100 \ times784} \ cdot \ boldsymbol {x} ^ {784} $$ exibição $$
Além disso, os 100 números resultantes são repassados para a função de ativação - alguma função não linear - que afeta cada número separadamente. Por exemplo, sigmóide, tangente hiperbólica, ReLU e outros. A função de ativação é necessariamente não linear, caso contrário, a rede neural aprenderá apenas transformações simples.
Em seguida, os dados resultantes são novamente alimentados a uma camada totalmente conectada, mas com um número diferente de neurônios e novamente à função de ativação. Isso acontece várias vezes. A última camada da rede é a camada que produz a resposta. Nesse caso, a resposta são informações sobre o número na imagem.
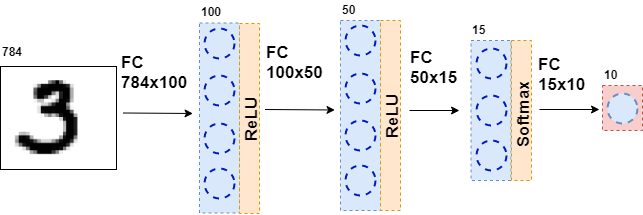
Durante o treinamento da rede, é necessário que saibamos qual figura é mostrada na figura. Ou seja, que o conjunto de dados está marcado. Então você pode usar outro elemento - a função de erro. Ela observa a resposta da rede neural e a compara com a resposta real. Graças a isso, a rede neural está aprendendo.
Declaração geral do problema
Todo o conjunto de dados é um tensor grande (chamaremos um conjunto de dados multidimensionais de tensor)
$ inline $ \ boldsymbol {X} = \ left [\ boldsymbol {x} _1, \ boldsymbol {x} _2, \ ldots, \ boldsymbol {x} _n \ right] $ inline $ onde
$ inline $ \ boldsymbol {x} _i $ inline $ - i-ésimo objeto, por exemplo, uma imagem, que também é um tensor. Para cada objeto existe
$ inline $ y_i $ inline $ - a resposta correta no i-ésimo objeto. Nesse caso, uma rede neural pode ser representada como uma função que recebe um objeto como entrada e fornece algumas respostas:
$$ display $$ F (\ boldsymbol {x} _i) = \ hat {y} _i $$ display $$
Agora vamos dar uma olhada mais de perto na função
$ inline $ F (\ boldsymbol {x} _i) $ inline $ . Como a rede neural consiste em camadas, cada camada individual é uma função. E isso significa
$$ display $$ F (\ boldsymbol {x} _i) = f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i)))) = \ hat {y} _i $$ display $ $
Ou seja, na primeira função - a primeira camada - uma imagem é apresentada na forma de algum tensor. Função
$ inline $ f_1 $ inline $ dá alguma resposta - também um tensor, mas de uma dimensão diferente. Este tensor será chamado de representação interna. Agora essa representação interna é alimentada na entrada da função
$ inline $ f_2 $ inline $ , que fornece sua representação interna. E assim por diante, até a função
$ inline $ f_k $ inline $ - última camada - não dará uma resposta
$ inline $ \ hat {y} _i $ inline $ .
Agora, a tarefa é treinar a rede - fazer a resposta da rede corresponder à resposta correta. Primeiro, você precisa medir o quão errada é a rede neural. Medir isso é uma função de erro.
$ inline $ L (\ hat {y} _i, y_i) $ inline $ . E impomos restrições:
1
$ inline $ \ hat {y} _i \ xrightarrow {} y_i \ Rightarrow L (\ hat {y} _i, y_i) \ xrightarrow {} 0 $ inline $
2)
$ inline $ \ existe ~ dL (\ hat {y} _i, y_i) $ inline $
3)
$ inline $ L (\ hat {y} _i, y_i) \ geq 0 $ inline $
A restrição 2 é imposta a todas as funções das camadas
$ inline $ f_j $ inline $ - sejam todos diferenciáveis.
Além disso, de fato (eu não mencionei isso), algumas dessas funções dependem dos parâmetros - os pesos da rede neural -
$ inline $ f_j (\ boldsymbol {x} _i | \ boldsymbol {\ omega} _j) $ inline $ . E a idéia toda é pegar esses pesos para que
$ inline $ \ hat {y} _i $ inline $ coincidiu com
$ inline $ y_i $ inline $ em todos os objetos de um conjunto de dados. Noto que nem todas as funções têm pesos.
Então, onde paramos? Todas as funções da rede neural são diferenciáveis, a função de erro também é diferenciável. Lembre-se de uma das propriedades do gradiente - mostre a direção do crescimento da função. Usamos isso, restrições 1 e 3, o fato de que
$$ display $$ L (F (\ boldsymbol {x} _i)) = L (f_k (f_ {k-1} (\ ldots (f_1 (\ boldsymbol {x} _i))))) = L (\ hat {y} _i) $$ exibir $$
e o fato de eu poder considerar derivadas parciais e derivadas de uma função complexa. Agora há tudo o que você precisa para calcular
$$ display $$ \ frac {\ L parcial (F (\ boldsymbol {x} _i))} {\ parcial \ boldsymbol {\ omega_j}} $$ display $$
para qualquer i e j. Essa derivada parcial mostra a direção na qual mudar
$ inline $ \ boldsymbol {\ omega_j} $ inline $ aumentar
$ inline $ L $ inline $ . Para reduzir, você precisa dar um passo para o lado
$ inline $ - \ frac {\ L parcial (F (\ boldsymbol {x} _i))} {\ parcial \ boldsymbol {\ omega_j}} $ inline $ nada complicado.
Isso significa que o processo de aprendizado de rede está estruturado da seguinte maneira: várias vezes em um ciclo, percorremos todo o conjunto de dados (isso é chamado de era), para cada objeto do conjunto de dados que consideramos
$ inline $ L (\ hat {y} _i, y_i) $ inline $ (isso é chamado de encaminhamento) e considere a derivada parcial
$ inline $ \ parcial L $ inline $ para todos os pesos
$ inline $ \ boldsymbol {\ omega_j} $ inline $ , atualize os pesos (isso é chamado de passagem para trás).
Noto que ainda não introduzi funções e camadas específicas. Se, nesta fase, não está claro o que fazer com tudo isso, proponho continuar lendo - haverá mais matemática, mas agora ela vai com exemplos.
Matemática Parte 2 (difícil)
Função de erro
Iniciarei do final e derivarei a função de erro para o problema de classificação. Para o problema de regressão, a derivação da função de erro está bem descrita no livro “Deep Learning. Imersão no mundo das redes neurais ".
Por uma questão de simplicidade, existe uma rede neural (NN) que separa as fotos de gatos das fotos de cães e há um conjunto de fotos de gatos e cães para os quais existe uma resposta correta
$ inline $ y_ {true} $ inline $ .
$$ display $$ NN (imagem | \ Omega) = y_ {pred} $$ display $$
Tudo o que farei a seguir é muito semelhante ao método da máxima verossimilhança. Portanto, a principal tarefa é encontrar a função de probabilidade. Se omitirmos os detalhes, uma função que compara a previsão da rede neural e a resposta correta e, se eles coincidem, gera um grande valor, se não, vice-versa. A probabilidade de uma resposta correta vem à mente com os parâmetros fornecidos:
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) $$ display $$
E agora vamos fazer uma finta, que, ao que parece, não segue de nenhum lugar. Deixe a rede neural dar uma resposta na forma de um vetor bidimensional, cuja soma dos valores é 1. O primeiro elemento desse vetor pode ser chamado de medida de confiança de que o gato está na foto e o segundo elemento, a medida de confiança de que o cachorro está na foto. Sim, é quase probabilidade!
$$ display $$ NN (imagem | \ Omega) = \ left [\ begin {matrix} p_0 \\ p_1 \\\ final {matrix} \ right] $$ display $$
Agora a função de probabilidade pode ser reescrita como:
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) = p_ \ Omega (y_ {pred}) ^ t_ {0} * (1 - p_ \ Omega (y_ {pred})) ^ t_ {1} = \\ p_0 ^ {t_0} * p_1 ^ {t_1} $$ display $$
Onde
$ inline $ t_0, t_1 $ inline $ rótulos da classe correta, por exemplo, se
$ inline $ y_ {true} = cat $ inline $ então
$ inline $ t_0 == 1, t_1 == 0 $ inline $ se
$ inline $ y_ {true} = cão $ inline $ então
$ inline $ t_0 == 0, t_1 == 1 $ inline $ . Assim, a probabilidade de uma classe que deveria ter sido prevista por uma rede neural (mas não necessariamente prevista por ela) é sempre considerada. Agora isso pode ser generalizado para qualquer número de classes (por exemplo, m classes):
$$ display $$ p (y_ {pred} = y_ {true} | \ Omega) = \ prod_0 ^ m p_i ^ {t_i} $$ display $$
No entanto, em qualquer conjunto de dados, existem muitos objetos (por exemplo, N objetos). Quero que a rede neural dê a resposta correta em cada um ou na maioria dos objetos. E para isso, você precisa multiplicar os resultados da fórmula acima para cada objeto do conjunto de dados.
$$ display $$ MaximumLikelyhood = \ prod_ {j = 0} ^ N \ prod_ {i = 0} ^ m p_ {i, j} ^ {t_ {i, j}} $$ display $$
Para obter bons resultados, essa função precisa ser maximizada. Mas, primeiro, é mais íngreme minimizar, porque temos uma descida gradiente estocástica e todos os pães para ele - basta atribuir um sinal de menos e, segundo, é difícil trabalhar com um trabalho enorme - é o logaritmo.
$$ display $$ CrossEntropyLoss = - \ soma \ limites_ {j = 0} ^ {N} \ soma \ limites_ {i = 0} ^ {m} t_ {i, j} \ cdot \ log (p_ {i, j }) $$ display $$
Ótimo! O resultado foi entropia cruzada ou, no caso binário, perda de log. Essa função é fácil de contar e ainda mais fácil de diferenciar:
$$ display $$ \ frac {\ parcial CrossEntropyLoss} {\ parcial p_j} = - \ frac {\ boldsymbol {t_j}} {\ boldsymbol {p_ {j}}} $$ display $$
Você precisa se diferenciar no algoritmo de retropropagação. Noto que a função de erro não altera a dimensão do vetor. Se, como no caso do MNIST, a saída for um vetor 10-dimensional de respostas, ao calcular a derivada, obteremos um vetor 10-dimensional de derivadas. Outra coisa interessante é que apenas um elemento da derivada não será zero, no qual
$ inline $ t_ {i, j} \ neq 0 $ inline $ , ou seja, com a resposta correta. E quanto menor a probabilidade de uma resposta correta prevista por uma rede neural em um determinado objeto, mais a função de erro estará nela.
Recursos de ativação
Na saída de cada camada totalmente conectada de uma rede neural, uma função de ativação não linear deve estar presente. Sem ele, é impossível treinar uma rede neural significativa. No futuro, uma camada totalmente conectada de uma rede neural é simplesmente uma multiplicação dos dados de entrada por uma matriz de peso. Na álgebra linear, isso é chamado de mapa linear - uma função linear. A combinação de funções lineares também é uma função linear. Mas isso significa que essa função pode apenas aproximar funções lineares. Infelizmente, não é por isso que são necessárias redes neurais.
Softmax
Normalmente, essa função é usada na última camada da rede, pois transforma o vetor da última camada em um vetor de “probabilidades”: cada elemento do vetor fica de 0 a 1 e sua soma é 1. Ele não altera a dimensão do vetor.
$$ display $$ Softmax_i = \ frac {e ^ {x_i}} {\ sum \ limits_ {j} e ^ {x_j}} $$ display $$
Agora vamos para a pesquisa derivada. Desde
$ inline $ \ boldsymbol {x} $ inline $ É um vetor, e todos os seus elementos estão sempre presentes no denominador; então, ao tomar a derivada, obtemos o Jacobiano:
$$ display $$ J_ {Softmax} = \ begin {cases} x_i - x_i \ cdot x_j, i = j \\ - x_i \ cdot x_j, i \ neq j \ end {cases} $$ display $$
Agora sobre retropropagação. O vetor de derivadas vem da camada anterior (geralmente essa é uma função de erro)
$ inline $ \ boldsymbol {dz} $ inline $ . Caso
$ inline $ \ boldsymbol {dz} $ inline $ veio de uma função de erro no mnist,
$ inline $ \ boldsymbol {dz} $ inline $ - vetor 10-dimensional. Então o jacobiano tem uma dimensão de 10x10. Para obter
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ , que vai além da camada anterior (não esqueça que passamos do final ao início da rede quando o erro se propaga de volta), precisamos multiplicar
$ inline $ \ boldsymbol {dz} $ inline $ em
$ inline $ J_ {Softmax} $ inline $ (linha por coluna):
$$ display $$ dz_ {new} = \ boldsymbol {dz} \ times J_ {Softmax} $$ display $$
Na saída, obtemos um vetor 10-dimensional de derivadas
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ .
Relu
$$ display $$ ReLU (x) = \ begin {cases} x, x> 0 \\ 0, x <0 \ end {cases} $$ display $$
O ReLU começou a ser utilizado em massa após 2011, quando foi publicado o artigo "Redes Neurais do Retificador Escasso Profundo". No entanto, essa função era conhecida anteriormente. O conceito de "poder de ativação" é aplicável ao ReLU (para obter mais detalhes, consulte o livro "Deep Learning. Imersão no mundo das redes neurais"). Mas o principal recurso que torna a ReLU mais atraente do que outras funções de ativação é seu simples cálculo derivativo:
$$ display $$ d (ReLU (x)) = \ begin {cases} 1, x> 0 \\ 0, x <0 \ end {cases} $$ display $$
Assim, ReLU é computacionalmente mais eficiente do que outras funções de ativação (sigmóide, tangente hiperbólica, etc.).
Camada totalmente conectada
Agora é a hora de discutir uma camada totalmente conectada. O mais importante de todos os outros, porque é nessa camada que estão localizados todos os pesos, que devem ser ajustados para que a rede neural funcione bem. Uma camada totalmente conectada é simplesmente uma matriz de peso:
$$ exibição $$ W = | w_ {i, j} | $$ exibição $$
Uma nova representação interna é obtida quando a matriz de pesos é multiplicada pela coluna de entrada:
$$ display $$ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $$ display $$
Onde
$ inline $ \ boldsymbol {x} $ inline $ tem tamanho
$ inline $ input \ _shape $ inline $ e
$ inline $ x_ {new} $ inline $ -
$ inline $ output \ _shape $ inline $ . Por exemplo
$ inline $ \ boldsymbol {x} $ inline $ - vetor 784 dimensional, e
$ inline $ \ boldsymbol {x} _ {new} $ inline $ É um vetor 100-dimensional, então a matriz W tem um tamanho de 100x784. Acontece que nessa camada há 100x784 = 78.400 pesos.
Com a propagação reversa do erro, é preciso levar a derivada em relação a cada peso dessa matriz. Simplifique o problema e use apenas a derivada com relação a
$ inline $ w_ {1,1} $ inline $ . Ao multiplicar a matriz e o vetor, o primeiro elemento do novo vetor
$ inline $ \ boldsymbol {x} _ {new} $ inline $ é igual a
$ inline $ x_ {new ~ 1} = w_ {1,1} \ cdot x_1 + ... + w_ {1.784} \ cdot x_ {784} $ inline $ e o derivado
$ inline $ x_ {new ~ 1} $ inline $ por
$ inline $ w_ {1,1} $ inline $ vai ser simples
$ inline $ x_1 $ inline $ , você só precisa obter a derivada do valor acima. Da mesma forma acontece para todos os outros pesos. Mas este não é um algoritmo de propagação de erro, desde que seja apenas uma matriz de derivadas. Você precisa se lembrar que da próxima camada a esta (o erro vai do fim ao começo) vem um vetor de gradiente 100-dimensional
$ inline $ d \ boldsymbol {z} $ inline $ . Primeiro elemento deste vetor
$ inline $ dz_1 $ inline $ será multiplicado por todos os elementos da matriz de derivativos que "participaram" da criação
$ inline $ x_ {new ~ 1} $ inline $ , ou seja, em
$ inline $ x_1, x_2, ..., x_ {784} $ inline $ . Da mesma forma, o resto dos elementos. Se você traduzir isso para o idioma da álgebra linear, será escrito assim:
exibição $$ $$ \ frac {\ L parcial} {\ parcial W} = (d \ boldsymbol {z}, ~ dW) = \ left (\ begin {matrix} dz_ {1} \ cdot \ boldsymbol {x} \ \ ... \\ dz_ {100} \ cdot \ boldsymbol {x} \ end {matrix} \ right) _ {100} $$ display $$
A saída é uma matriz 100x784.
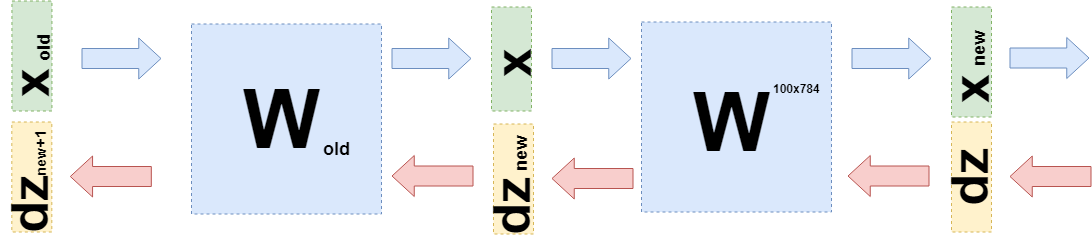
Agora você precisa entender o que transferir para a camada anterior. Para isso e para uma melhor compreensão do que aconteceu agora, quero anotar o que aconteceu ao obter derivativos nessa camada em uma linguagem um pouco diferente, para me afastar das especificidades do “o que é multiplicado” pelas funções (novamente).
Quando eu queria ajustar os pesos, queria usar a derivada da função de erro para esses pesos:
$ inline $ \ frac {\ L parcial \ {W parcial W} $ inline $ . Foi mostrado acima como obter derivadas de funções de erro e funções de ativação. Portanto, podemos considerar esse caso (em
$ inline $ d \ boldsymbol {z} $ inline $ todas as derivadas da função de erro e das funções de ativação já estão paradas):
$$ display $$ \ frac {\ L parcial} {\ W parcial} = d \ boldsymbol {z} \ cdot \ frac {\ parcial \ boldsymbol {x} _ {novo} (W)} {\ W parcial} $ $ display $$
Isso pode ser feito, porque você pode considerar
$ inline $ \ boldsymbol {x} _ {new} $ inline $ em função de W:
$ inline $ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $ inline $ .
Você pode substituir isso na fórmula acima:
exibição $$ $$ \ frac {\ L parcial \ {W parcial} = d \ boldsymbol {z} \ cdot \ frac {\ parcial W \ cdot \ boldsymbol {x}} {\ parcial W} = d \ boldsymbol { z} \ cdot E \ cdot \ boldsymbol {x} $$ display $$
Onde E é uma matriz que consiste em unidades (NÃO é uma matriz de unidades).
Agora, quando você precisar obter a derivada da camada anterior (mesmo que por simplicidade de cálculos, ela também seja uma camada totalmente conectada, mas, no caso geral, não altera nada), é necessário considerar
$ inline $ \ boldsymbol {x} $ inline $ em função da camada anterior
$ inline $ \ boldsymbol {x} (W_ {old}) $ inline $ :
exibição $$ $$ \ begin {reunido} \ frac {\ L parcial \ {L} parcial} = d \ símbolo de negrito {z} \ cdot \ frac {\ símbolo de negrito parcial {x} _ {novo} (W )} {\ W_ parcial {antigo}} = d \ boldsymbol {z} \ cdot \ frac {\ W \ cdot parcial \ boldsymbol {x} (W_ {old})} {\ W_ parcial {old}} = \\ = d \ boldsymbol {z} \ cdot \ frac {\ W parcial \ cdot W_ {antigo} \ cdot \ boldsymbol {x} _ {antigo}} {\ W parcial {antigo}} = d \ boldsymbol {z} \ cdot W \ cdot E \ cdot \ boldsymbol {x} _ {antigo} = \\ = d \ boldsymbol {z} _ {novo} \ cdot E \ cdot \ boldsymbol {x} _ {antigo} \ end {reunido} $$ exibir $$
Exatamente
$ inline $ d \ boldsymbol {z} _ {new} = d \ boldsymbol {z} \ cdot W $ inline $ e você precisa enviar para a camada anterior.
Código
Este artigo tem como objetivo principal explicar a matemática das redes neurais. Dedicarei muito pouco tempo ao código.
Este é um exemplo de implementação da função de erro:
class CrossEntropy: def forward(self, y_true, y_hat): self.y_hat = y_hat self.y_true = y_true self.loss = -np.sum(self.y_true * np.log(y_hat)) return self.loss def backward(self): dz = -self.y_true / self.y_hat return dz
A classe possui métodos para passagem direta e reversa. No momento do passe direto, a instância da classe armazena os dados dentro da camada e, no momento do passe de retorno, os usa para calcular o gradiente. As demais camadas são construídas da mesma maneira. Graças a isso, torna-se possível escrever um neural totalmente conectado neste estilo:
class MnistNet: def __init__(self): self.d1_layer = Dense(784, 100) self.a1_layer = ReLu() self.drop1_layer = Dropout(0.5) self.d2_layer = Dense(100, 50) self.a2_layer = ReLu() self.drop2_layer = Dropout(0.25) self.d3_layer = Dense(50, 10) self.a3_layer = Softmax() def forward(self, x, train=True): ... def backward(self, dz, learning_rate=0.01, mini_batch=True, update=False, len_mini_batch=None): ...
O código completo pode ser encontrado
aqui .
Também aconselho a estudar este
artigo sobre Habré .
Conclusão
Espero ter sido capaz de explicar e mostrar que a matemática bastante simples está por trás das redes neurais e que isso não é nada assustador. No entanto, para uma compreensão mais profunda, vale a pena tentar escrever sua própria “bicicleta”. Correções e sugestões são felizes em ler nos comentários.