Redes neurais e aprendizado profundo, capítulo 3, parte 3: como escolher hiperparâmetros de redes neurais?

Até agora, não expliquei como escolho os valores dos hiperparâmetros - a taxa de aprendizado η, o parâmetro de regularização λ e assim por diante. Eu apenas dei bons valores de trabalho. Na prática, quando você usa uma rede neural para atacar um problema, pode ser difícil encontrar bons hiperparâmetros. Imagine, por exemplo, que acabamos de nos informar sobre o problema do MNIST, e começamos a trabalhar nele, sem saber nada sobre os valores de hiperparâmetros adequados. Suponhamos que tivemos sorte por acaso, e nos primeiros experimentos, escolhemos muitos hiperparâmetros, como já fizemos neste capítulo: 30 neurônios ocultos, um tamanho de minipacote de 10, treinamento para 30 épocas e o uso de entropia cruzada. No entanto, escolhemos a taxa de aprendizado η = 10,0 e o parâmetro de regularização λ = 1000,0. E aqui está o que eu vi com essa corrida:

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10]) >>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 1030 / 10000 Epoch 1 training complete Accuracy on evaluation data: 990 / 10000 Epoch 2 training complete Accuracy on evaluation data: 1009 / 10000 ... Epoch 27 training complete Accuracy on evaluation data: 1009 / 10000 Epoch 28 training complete Accuracy on evaluation data: 983 / 10000 Epoch 29 training complete Accuracy on evaluation data: 967 / 10000 

Nossa classificação não funciona melhor que a amostragem aleatória! Nossa rede funciona como um gerador de ruído aleatório!

"Bem, isso é fácil de consertar", você poderia dizer, "basta reduzir os hiperparâmetros, como velocidade de aprendizado e regularização". Infelizmente, a priori, você não tem informações sobre o que exatamente esses hiperparâmetros você precisa ajustar. Talvez o principal problema seja que nossos 30 neurônios ocultos nunca funcionem, independentemente de como os outros hiperparâmetros sejam selecionados? Talvez precisemos de pelo menos 100 neurônios ocultos? Ou 300? Ou muitas camadas ocultas? Ou uma abordagem diferente para codificação de saída? Talvez nossa rede esteja aprendendo, mas precisamos treiná-la mais épocas? Talvez o tamanho dos mini pacotes seja muito pequeno? Talvez tivéssemos feito melhor se retornássemos à função quadrática do valor? Talvez precisemos tentar uma abordagem diferente para inicializar pesos? E assim por diante e assim por diante. No espaço dos hiperparâmetros, é fácil se perder. E isso pode trazer muitos inconvenientes se a sua rede for muito grande ou usar grandes quantidades de dados de treinamento, e você poderá treiná-lo por horas, dias ou semanas sem receber resultados. Em tal situação, sua confiança começa a passar. Talvez as redes neurais tenham sido a abordagem errada para resolver seu problema? Talvez você pare e faça apicultura?

Nesta seção, explicarei algumas abordagens heurísticas que você pode usar para configurar hiperparâmetros em uma rede neural. O objetivo é ajudá-lo a elaborar um fluxo de trabalho que permita configurar muito bem os hiperparâmetros. Obviamente, não posso cobrir todo o tópico da otimização do hiperparâmetro. Essa é uma área enorme e não é um problema que possa ser resolvido completamente, ou existe um acordo geral sobre as estratégias corretas para resolvê-lo. Sempre há a oportunidade de tentar outro truque para extrair resultados extras da sua rede neural. Mas as heurísticas nesta seção devem fornecer um ponto de partida.

Estratégia geral

Ao usar uma rede neural para atacar um novo problema, a primeira dificuldade é obter resultados não triviais da rede, ou seja, excedendo uma probabilidade aleatória. Isso pode ser surpreendentemente difícil, especialmente quando você se depara com uma nova classe de tarefas. Vejamos algumas estratégias que podem ser usadas para esse tipo de dificuldade.

Suponha, por exemplo, que você seja o primeiro a atacar a tarefa MNIST. Você começa com grande entusiasmo, mas a falha completa da sua primeira rede é um pouco desanimadora, conforme descrito no exemplo acima. Então você precisa desmontar o problema em partes. Você precisa se livrar de todo o treinamento e imagens de suporte, exceto imagens de zeros e uns. Em seguida, tente treinar a rede para distinguir 0 de 1. Essa tarefa não é apenas essencialmente mais fácil do que distinguir todos os dez dígitos, mas também reduz a quantidade de dados de treinamento em 80%, acelerando o aprendizado em 5 vezes. Isso permite realizar experimentos muito mais rapidamente e oferece a oportunidade de entender rapidamente como criar uma boa rede.

As experiências podem ser aceleradas ainda mais, reduzindo a rede a um tamanho mínimo que provavelmente será treinado de maneira significativa. Se você acha que é provável que a rede [784, 10] seja capaz de classificar os dígitos do MNIST melhor que uma amostra aleatória, comece a experimentar. Vai ser muito mais rápido que o treinamento [784, 30, 10], e você já pode fazer isso mais tarde.

Outra aceleração dos experimentos pode ser obtida aumentando a frequência do rastreamento. No programa network2.py, monitoramos a qualidade do trabalho no final de cada época. Ao processar 50.000 imagens por época, precisamos esperar um tempo bastante longo - cerca de 10 segundos por época no meu laptop durante o treinamento em rede [784, 30, 10] - antes de obter feedback sobre a qualidade do treinamento em rede. É claro que dez segundos não são tão longos, mas se você quiser experimentar várias dezenas de hiperparâmetros diferentes, isso começará a incomodar e, se você quiser experimentar centenas ou milhares de opções, isso será devastador. O feedback pode ser recebido muito mais rapidamente, rastreando a precisão da confirmação com mais frequência, por exemplo, a cada 1.000 imagens de treinamento. Além disso, em vez de usar o conjunto completo de 10.000 imagens de confirmação, podemos obter uma estimativa muito mais rápida usando apenas 100 imagens de confirmação. O principal é que a rede vê imagens suficientes para realmente aprender e obter uma estimativa suficientemente boa da eficácia. Obviamente, nosso network2.py ainda não fornece esse rastreamento. Porém, como muletas para alcançar esse efeito com fins ilustrativos, recortamos nossos dados de treinamento para as primeiras 1000 imagens MNIST. Vamos tentar ver o que acontece (para simplificar o código, não usei a ideia de deixar apenas as imagens 0 e 1 - isso também pode ser realizado com um pouco mais de esforço).

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 ... 

Ainda temos ruído puro, mas temos uma grande vantagem: o feedback é atualizado em frações de segundo e não a cada dez segundos. Isso significa que você pode experimentar muito mais rapidamente com a seleção de hiperparâmetros, ou mesmo experimentar com muitos hiperparâmetros diferentes quase simultaneamente.

No exemplo acima, deixei o valor de λ igual a 1000,0, como antes. Porém, como alteramos o número de exemplos de treinamento, precisamos alterar λ para que o enfraquecimento dos pesos seja o mesmo. Isso significa que mudamos λ em 20,0. Nesse caso, obtemos o seguinte:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 12 / 100 Epoch 1 training complete Accuracy on evaluation data: 14 / 100 Epoch 2 training complete Accuracy on evaluation data: 25 / 100 Epoch 3 training complete Accuracy on evaluation data: 18 / 100 ... 

Sim! Nós temos um sinal. Não é particularmente bom, mas existe. Isso já pode ser tomado como ponto de partida e altere os hiperparâmetros para tentar obter mais melhorias. Suponha que decidimos que precisamos aumentar a velocidade do aprendizado (como você provavelmente entendeu, decidimos incorretamente, pelo motivo que discutiremos mais adiante, mas vamos tentar fazer isso por enquanto). Para testar nosso palpite, giramos η para 100,0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 10 / 100 Epoch 1 training complete Accuracy on evaluation data: 10 / 100 Epoch 2 training complete Accuracy on evaluation data: 10 / 100 Epoch 3 training complete Accuracy on evaluation data: 10 / 100 ... 

Tudo está ruim! Aparentemente, nosso palpite estava incorreto e o problema não estava no valor muito baixo da velocidade de aprendizado. Tentamos apertar η para um pequeno valor de 1,0:

 >>> net = network2.Network([784, 10]) >>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \ ... evaluation_data=validation_data[:100], \ ... monitor_evaluation_accuracy=True) Epoch 0 training complete Accuracy on evaluation data: 62 / 100 Epoch 1 training complete Accuracy on evaluation data: 42 / 100 Epoch 2 training complete Accuracy on evaluation data: 43 / 100 Epoch 3 training complete Accuracy on evaluation data: 61 / 100 ... 

Isso é melhor! E assim podemos continuar, torcendo cada hiperparâmetro e melhorando gradualmente a eficiência. Tendo estudado a situação e encontrado um valor aprimorado para η, prosseguimos na busca de um bom valor para λ. Em seguida, realizaremos um experimento com uma arquitetura mais complexa, por exemplo, com uma rede de 10 neurônios ocultos. Então, novamente ajustamos os parâmetros para η e λ. Então aumentaremos a rede para 20 neurônios ocultos. Um pouco de ajuste nos hiperparâmetros. E assim por diante, avaliando a eficácia em cada etapa usando parte de nossos dados de suporte e usando essas estimativas para selecionar todos os melhores hiperparâmetros. No processo de aprimoramentos, leva cada vez mais tempo para ver o efeito do ajuste de hiperparâmetros, para que possamos reduzir gradualmente a frequência de rastreamento.

Como estratégia geral, essa abordagem parece promissora. No entanto, quero voltar ao primeiro passo na busca de hiperparâmetros que permitam à rede aprender pelo menos de alguma forma. De fato, mesmo no exemplo acima, a situação era otimista demais. Trabalhar com uma rede que não aprende nada pode ser extremamente irritante. Você pode ajustar os hiperparâmetros por vários dias e não receber respostas significativas. Portanto, gostaria de enfatizar mais uma vez que, nos estágios iniciais, é necessário garantir um feedback rápido das experiências. Intuitivamente, pode parecer que simplificar o problema e a arquitetura apenas o atrasará. De fato, isso acelera o processo, porque você pode encontrar uma rede com um sinal significativo muito mais rápido. Depois de receber esse sinal, você poderá obter rapidamente melhorias ao ajustar os hiperparâmetros. Como em muitas situações da vida, o mais difícil é iniciar o processo.

Ok, esta é uma estratégia geral. Agora, vamos dar uma olhada nas recomendações específicas para prescrever hiperparâmetros. Vou me concentrar na velocidade de aprendizado η, no parâmetro de regularização L2 λ e no tamanho do minipacote. No entanto, muitos comentários serão aplicáveis ​​a outros hiperparâmetros, incluindo aqueles relacionados à arquitetura de rede, outras formas de regularização e alguns hiperparâmetros, que aprenderemos mais adiante no livro, por exemplo, o coeficiente de momento.

Velocidade de aprendizagem

Suponha que tenhamos lançado três redes MNIST com três velocidades de aprendizado diferentes, η = 0,025, η = 0,25 e η = 2,5, respectivamente. Deixamos os hiperparâmetros restantes como estavam nas seções anteriores - 30 eras, o tamanho do minipacote é 10, λ = 5,0. Também voltaremos a usar todas as 50.000 imagens de treinamento. Aqui está um gráfico mostrando o comportamento do custo do treinamento (criado pelo programa multiple_eta.py):



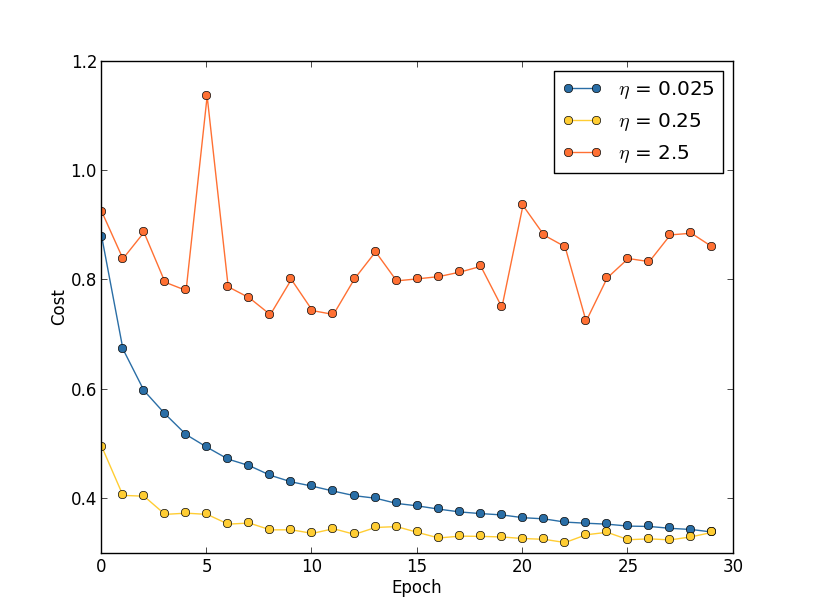
Em η = 0,025, o custo diminui suavemente até a última era. Com η = 0,25, o custo inicialmente diminui, mas após 20 épocas ele fica saturado, de modo que a maioria das mudanças acaba sendo pequena e, obviamente, flutuações aleatórias. Com η = 2,5, o custo varia muito desde o início. Para entender o motivo dessas flutuações, lembramos que a descida do gradiente estocástico deve gradualmente nos levar ao vale da função de custo:



Essa imagem ajuda a imaginar intuitivamente o que está acontecendo, mas não é uma explicação completa e abrangente. Mais precisamente, mas brevemente, a descida do gradiente usa uma aproximação de primeira ordem para a função de custo para entender como reduzir o custo. Para η maior, os membros de uma função de custo de ordem mais alta se tornam mais importantes e podem dominar o comportamento interrompendo a descida do gradiente. Isso é especialmente provável quando se aproxima os mínimos e mínimos locais da função de custo, já que próximo a esses pontos o gradiente se torna pequeno, o que facilita o domínio de membros de uma ordem superior.

No entanto, se η for muito grande, as etapas serão tão grandes que poderão saltar um mínimo, devido ao qual o algoritmo subirá do vale. Provavelmente é isso que faz o preço oscilar em η = 2,5. A escolha de η = 0,25 leva ao fato de que as etapas iniciais realmente nos levam a um mínimo da função de custo, e somente quando chegamos a ela começamos a ter dificuldades com o salto. E quando escolhemos η = 0,025, não temos essas dificuldades durante as primeiras 30 épocas. Obviamente, a escolha de um valor tão pequeno de η cria outra dificuldade - ou seja, diminui a descida do gradiente estocástico. A melhor abordagem seria começar com η = 0,25, aprender 20 eras e depois ir para η = 0,025. Mais tarde, discutiremos essa taxa de aprendizado variável. Enquanto isso, vamos nos concentrar na questão de encontrar um valor adequado para a velocidade de aprendizado η.

Com isso em mente, podemos escolher η da seguinte maneira. Primeiro, avaliamos o valor limite η no qual o custo dos dados de treinamento começa imediatamente a diminuir, mas não flutua e não aumenta. Essa estimativa não precisa ser precisa. A ordem pode ser estimada começando com η = 0,01. Se o custo diminuir nas primeiras eras, vale a pena tentar η = 0,1, 1,0 e assim por diante, até encontrar um valor no qual o valor flutue ou aumente nas primeiras eras. E vice-versa, se o valor flutuar ou aumentar nas primeiras épocas com η = 0,01, tente η = 0,001, η = 0,0001, até encontrar o valor em que o custo diminui nas primeiras eras. Este procedimento fornecerá a ordem do valor limite η. Se desejar, você pode refinar sua avaliação escolhendo o valor mais alto para η, no qual o custo diminui nas primeiras épocas, por exemplo, η = 0,5 ou η = 0,2 (a ultraprecisão não é necessária aqui). Isso nos fornece uma estimativa do valor limite η.

O valor real de η, obviamente, não deve exceder o limite selecionado. De fato, para que o valor η permaneça útil por muitas épocas, é melhor usar um valor duas vezes menor que o limite. Essa escolha geralmente permite que você aprenda muitas épocas sem diminuir drasticamente o aprendizado.

No caso de dados MNIST, seguir esta estratégia levará a uma estimativa da ordem do limiar de η em 0,1. Após algum refinamento, obtemos o valor η = 0,5. Seguindo a receita acima, devemos usar η = 0,25 para nossa velocidade de aprendizado. Mas, na verdade, descobri que η = 0,5 funcionou bem por 30 épocas, então não estava preocupado em diminuí-lo.

Tudo isso parece bem direto. No entanto, usar o custo do treinamento para selecionar η parece contradizer o que eu disse anteriormente - que escolhemos hiperparâmetros, avaliando a eficácia da rede usando dados confirmatórios selecionados. De fato, usaremos a precisão da confirmação para selecionar os hiperparâmetros de regularização, o tamanho do minipacote e os parâmetros de rede, como o número de camadas e os neurônios ocultos, etc. Por que fazemos as coisas de maneira diferente com velocidade de aprendizado? Honestamente, essa escolha se deve às minhas preferências estéticas pessoais e provavelmente é tendenciosa. O argumento é que outros hiperparâmetros devem melhorar a precisão da classificação final no conjunto de testes, portanto, faz sentido escolhê-los com base na precisão da confirmação. No entanto, a taxa de aprendizado afeta indiretamente apenas a precisão da classificação final. Seu principal objetivo é controlar o tamanho da etapa da descida do gradiente e acompanhar o custo do treinamento da melhor maneira para reconhecer um tamanho de etapa muito grande. Mas ainda assim, essa é uma preferência estética pessoal. Nos estágios iniciais do treinamento, o custo do treinamento geralmente diminui apenas se a precisão da confirmação aumentar; portanto, na prática, não deve importar quais critérios usar.

Usando uma parada antecipada para determinar o número de eras de treinamento

Como mencionamos neste capítulo, uma parada antecipada significa que, no final de cada era, precisamos calcular a precisão da classificação nos dados de suporte. Quando deixa de melhorar, paramos de trabalhar. Como resultado, definir o número de épocas se torna um assunto simples. Em particular, isso significa que não precisamos descobrir especificamente como o número de épocas depende de outros hiperparâmetros. Isso acontece automaticamente. Além disso, uma parada antecipada também nos impede automaticamente de reciclagem. Isso, é claro, é bom, embora possa ser útil desativar a parada inicial nos estágios iniciais das experiências, para que você possa ver sinais de reciclagem e usá-los para ajustar a abordagem da regularização.

Para implementar o RO, precisamos descrever mais especificamente o que significa "parar a melhoria da precisão da classificação". Como vimos, a precisão pode ir muito longe, mesmo quando a tendência geral está melhorando. Se pararmos pela primeira vez, quando a precisão diminuir, quase certamente não alcançaremos possíveis melhorias adicionais. A melhor abordagem é interromper o aprendizado se a melhor precisão da classificação não melhorar por um longo tempo. Suponha, por exemplo, que estamos envolvidos no MNIST. Então, podemos decidir interromper o processo se a precisão da classificação não tiver melhorado nas últimas dez épocas. Isso garante que não paremos muito cedo devido a uma falha no treinamento, mas não esperaremos para sempre as melhorias que não acontecerão.

Esta regra de “nenhuma melhoria em mais de dez épocas” é adequada para o estudo inicial do MNIST. No entanto, às vezes as redes podem atingir um platô próximo a uma certa precisão de classificação, permanecer por algum tempo e começar a melhorar novamente. Se você precisar obter um desempenho muito bom, a regra "nenhuma melhoria em mais de dez épocas" pode ser muito agressiva para isso. Portanto, recomendo usar a regra "sem melhoria em dez épocas" para experimentos primários e adotar regras mais brandas quando você começar a entender melhor o comportamento da sua rede: "nenhuma melhoria em vinte épocas", "nenhuma melhoria em cinquenta épocas" e assim por diante mais adiante. Obviamente, isso nos fornece outro hiperparâmetro para otimização! Mas, na prática, esse hiperparâmetro é geralmente fácil de ajustar para obter bons resultados. E para tarefas que não sejam o MNIST, a regra “sem melhoria em dez épocas” pode ser muito agressiva ou não agressiva o suficiente, dependendo dos detalhes de uma tarefa específica.No entanto, depois de experimentar um pouco, geralmente é bastante fácil encontrar uma estratégia adequada de parada precoce.

Ainda não usamos uma parada precoce em nossos experimentos com o MNIST. Isso se deve ao fato de termos feito muitas comparações de diferentes abordagens de aprendizagem. Para essas comparações, é útil usar o mesmo número de épocas em todos os casos. No entanto, vale a pena alterar o network2.py introduzindo o RO no programa.

As tarefas

• Modifique network2.py para que o pedido apareça lá de acordo com a regra "sem alteração para n épocas", em que n é um parâmetro configurável.
• Pense em uma regra de parada antecipada que não seja "inalterada em épocas". Idealmente, a regra deve buscar um compromisso entre obter precisão com alta confirmação e um tempo de treinamento bastante curto. Adicione uma regra ao network2.py e execute três experimentos comparando a precisão da validação e o número de eras de treinamento com a regra "sem alteração acima de 10 eras".

Plano de Mudança da Velocidade de Aprendizagem

Enquanto mantivemos a velocidade de aprendizado η constante. No entanto, geralmente é útil modificá-lo. Nos estágios iniciais do processo de treinamento, é mais provável que os pesos sejam atribuídos completamente errados. Portanto, será melhor usar uma alta taxa de treinamento, o que fará com que os pesos mudem mais rapidamente. Depois, você pode reduzir a velocidade do treinamento para fazer um ajuste mais preciso das escalas.

Como delineamos um plano para mudar a velocidade do aprendizado? Aqui você pode aplicar muitas abordagens. Uma opção natural é usar a mesma idéia básica que no RO. Mantemos a velocidade de aprendizado constante até que a precisão da confirmação comece a se deteriorar. Em seguida, reduzimos o CO em uma certa quantia, digamos, duas ou dez vezes. Repetimos isso várias vezes até que o CO seja 1024 (ou 1000) vezes menor que o inicial. E termine o treinamento.

Um plano para alterar a velocidade de aprendizado pode melhorar a eficiência e também abre enormes oportunidades para a escolha de um plano. E isso pode ser uma dor de cabeça - você pode gastar para sempre otimizar o plano. Para os primeiros experimentos, sugiro usar um valor único e constante de CO. Isso lhe dará uma boa primeira aproximação. Mais tarde, se você quiser extrair a melhor eficiência da rede, vale a pena experimentar o plano de alterar a velocidade de aprendizado conforme eu a descrevi. Um trabalho científico bastante fácil de ler de 2010 demonstra as vantagens de velocidades variáveis ​​de aprendizado ao atacar o MNIST.

Exercício

• Modifique network2.py para que ele implemente o seguinte plano para alterar a velocidade de aprendizado: reduza pela metade o CR sempre que a precisão da confirmação satisfizer a regra "nenhuma alteração em 10 épocas" e pare de aprender quando a velocidade de aprendizado cair para 1/128 em relação à inicial.

O parâmetro de regularização λ

Eu recomendo começar sem nenhuma regularização (λ = 0,0) e determinar o valor de η, como indicado acima. Usando o valor selecionado de η, podemos usar os dados de suporte para selecionar um bom valor de λ. Comece com λ = 1,0 (não tenho um bom argumento a favor dessa escolha) e aumente ou diminua em 10 vezes para aumentar a eficiência no trabalho com dados de confirmação. Tendo encontrado a ordem correta de magnitude, podemos ajustar o valor de λ com mais precisão. Depois disso, é necessário retornar à otimização η novamente.

Exercício

• , , λ η. , λ? , η?

Se você usar as recomendações desta seção, verá que os valores selecionados de η e λ nem sempre correspondem exatamente aos que usei anteriormente. Só que o livro tem limitações de texto, o que às vezes tornava impraticável otimizar os hiperparâmetros. Lembre-se de todas as comparações das diferentes abordagens de treinamento em que estamos trabalhando - comparando a função de custo quadrático e entropia cruzada, métodos antigos e novos de inicialização de pesos, iniciando com e sem regularização e assim por diante. Para tornar essas comparações significativas, tentei não alterar os hiperparâmetros entre as abordagens comparadas (ou escalá-las corretamente). Obviamente, não há razão para que os mesmos hiperparâmetros sejam ótimos para todas as abordagens diferentes de aprendizado; portanto, os hiperparâmetros que utilizo foram o resultado de um compromisso.

Como alternativa, eu poderia tentar otimizar todos os hiper parâmetros para cada abordagem de aprendizado ao máximo. Seria uma abordagem melhor e mais honesta, já que tiraríamos o melhor de cada uma das abordagens da aprendizagem. No entanto, fizemos dezenas de comparações e, na prática, isso seria muito caro computacionalmente. Portanto, decidi comprometer-me a usar opções de hiperparâmetro boas o suficiente (mas não necessariamente ótimas).

Mini tamanho da embalagem

Como escolher o tamanho da minipacote? Para responder a essa pergunta, primeiro vamos assumir que estamos envolvidos em treinamento on-line, ou seja, usamos um mini-pacote de tamanho 1.

O problema óbvio do aprendizado on-line é que o uso de mini-pacotes que consistem em um único exemplo de treinamento levará a erros graves na estimativa do gradiente. Mas, de fato, esses erros não apresentarão um problema tão sério. A razão é que as estimativas individuais de gradiente não precisam ser altamente precisas. Só precisamos obter uma estimativa suficientemente precisa para que nossa função de custo diminua. É como se você estivesse tentando chegar ao pólo magnético norte, mas teria uma bússola não confiável, com cada medição confundida em 10 a 20 graus. Se você verificar a bússola com bastante frequência e, em média, indicar a direção certa, você poderá chegar ao pólo magnético norte.

Diante desse argumento, parece que devemos usar o aprendizado on-line. Mas, na realidade, a situação é um pouco mais complicada. Na tarefa do capítulo anterior, apontei que, para calcular a atualização de gradiente para todos os exemplos no mini-pacote, você pode usar técnicas de matriz ao mesmo tempo, em vez de um loop. Dependendo dos detalhes do seu hardware e da biblioteca de álgebra linear, pode ser muito mais rápido calcular a estimativa para o minipacote de, digamos, 100 do que calcular a estimativa de gradiente para o minipacote em um ciclo para 100 exemplos de treinamento. Pode ser, por exemplo, apenas 50 vezes mais lento, e não 100.

A princípio, parece que isso não ajuda muito. Com um tamanho de minipacote de 100, a regra de treinamento para pesos se parece com:

$$

$$w \rightarrow w' = w-\eta \frac{1}{100} \sum_x \nabla C_x \tag{100}$$

onde a soma vai sobre os exemplos de treinamento no minipacote. Compare com

$$

$$w \rightarrow w' = w-\eta \nabla C_x \tag{101}$$

para aprendizado online. Mesmo que demore 50 vezes mais tempo para atualizar o mini-pacote, o treinamento on-line ainda parece ser a melhor opção, pois seremos atualizados com mais frequência. Mas suponha, no entanto, que, no caso do mini-pacote, aumentemos a velocidade de aprendizado em 100 vezes, a regra de atualização se transformará em:

$$

$$w \rightarrow w' = w-\eta \sum_x \nabla C_x \tag{102}$$

É semelhante a 100 estágios separados de aprendizado on-line com uma velocidade de aprendizado de η. No entanto, um passo no aprendizado on-line leva apenas 50 vezes mais tempo. Obviamente, na realidade, esses não são exatamente 100 níveis de aprendizado on-line, pois no minipacote todos os ∇C _x são avaliados para o mesmo conjunto de pesos, em contraste com o aprendizado acumulado que ocorre no caso on-line. E, no entanto, parece que o uso de mini-pacotes maiores acelerará o processo.

Dados todos esses fatores, a escolha do melhor tamanho de minipacote é um compromisso. Escolha muito pequeno e não obtenha todos os benefícios de boas bibliotecas matriciais otimizadas para hardware rápido. Escolha muito grande e não atualizará o peso com frequência suficiente. Você precisa escolher um valor de compromisso que maximize a velocidade de aprendizado. Felizmente, a escolha do tamanho do minipacote na qual a velocidade é maximizada é relativamente independente de outros hiperparâmetros (exceto para a arquitetura geral); portanto, para encontrar um bom tamanho de minipacote, não é necessário otimizá-los. Portanto, será suficiente usar valores aceitáveis ​​(não necessariamente ótimos) para outros hiperparâmetros e tentar vários tamanhos diferentes de minipacotes, escalando η, conforme indicado acima.Crie um gráfico da precisão da confirmação versus o tempo (tempo real decorrido, não as apagadas!) E escolha um tamanho de minipacote que ofereça a melhoria mais rápida do desempenho. Com o tamanho de minipacote selecionado, você pode otimizar outros hiperparâmetros.

Obviamente, como você já entendeu, sem dúvida, em nosso trabalho não realizei essa otimização. Em nossa implementação da Assembléia Nacional, uma abordagem rápida para atualizar mini-pacotes não é usada. Simplesmente usei o tamanho do minipacote 10 sem comentar ou explicar, em quase todos os exemplos. Em geral, podemos acelerar o aprendizado reduzindo o tamanho do minipacote. Eu não fiz isso, em particular, porque meus experimentos preliminares sugeriram que a aceleração seria bastante modesta. Mas em implementações práticas, definitivamente gostaríamos de implementar a abordagem mais rápida para atualizar mini-pacotes e tentar otimizar seu tamanho para maximizar a velocidade geral.

Técnicas automatizadas

Descrevi essas abordagens heurísticas como algo que precisa ser ajustado manualmente. A otimização manual é uma boa maneira de ter uma idéia de como o NS funciona. No entanto, e, aliás, não surpreende que muito trabalho já tenha sido feito na automação deste projeto. Uma técnica comum é uma pesquisa de grade que peneira sistematicamente uma grade no espaço dos hiperparâmetros. Uma visão geral das realizações e limitações dessa técnica (bem como recomendações sobre alternativas facilmente implementáveis) pode ser encontrada em 2012 . Muitas técnicas sofisticadas foram propostas. Não vou revisar todos eles, mas quero observar o trabalho promissor de 2012, usando a otimização bayesiana de hiperparâmetros. O código do trabalho está aberto a todos , e com algum sucesso foi usado por outros pesquisadores.

Resumir

Usando as regras de prática que descrevi, você não obterá os melhores resultados do seu PS de todos os possíveis. Mas é provável que eles forneçam um bom ponto de partida e base para novas melhorias. Em particular, descrevi basicamente os hiperparâmetros de forma independente. Na prática, há uma conexão entre eles. Você pode experimentar com η, decidir que encontrou o valor correto, começar a otimizar λ e descobrir que ele viola sua otimização η. Na prática, é útil avançar em diferentes direções, aproximando-se gradualmente de bons valores. Acima de tudo, lembre-se de que as abordagens heurísticas que descrevi são regras simples de prática, mas não algo esculpido em pedra. Você precisa procurar sinais de que algo não está funcionando e deseja experimentar. Em particularmonitore cuidadosamente o comportamento da sua rede neural, especialmente a precisão da confirmação.

A complexidade da escolha dos hiperparâmetros é agravada pelo fato de que o conhecimento prático de sua escolha está espalhado por muitos trabalhos e programas de pesquisa, e geralmente está apenas na cabeça de cada profissional. Há uma enorme quantidade de trabalho com descrições do que fazer (geralmente conflitando entre si). No entanto, existem vários trabalhos particularmente úteis que sintetizam e destacam grande parte desse conhecimento. No Joshua Benji a partir de 2012 dá conselhos práticos sobre o uso de back-propagação gradiente descendente e treinamento para a Assembleia Nacional, incluindo a Assembleia Nacional e profundo. Benjio descreve muitos dos detalhes com muito mais detalhes. Do que eu, incluindo uma busca sistemática por hiperparâmetros. Outro bom trabalho é o trabalho.Yanna Lekuna e outros, 1998. Ambos os trabalhos aparecem no livro extremamente útil de 2012, que contém muitos truques frequentemente usados ​​na Assembléia Nacional: " Redes neurais: truques de artesanato ". O livro é caro, mas muitos de seus artigos foram publicados na Internet por seus autores e podem ser encontrados nos motores de busca.

A partir desses artigos, e especialmente de nossos próprios experimentos, uma coisa fica clara: o problema de otimizar hiperparâmetros não pode ser chamado de completamente resolvido. Sempre há outro truque que você pode tentar melhorar a eficiência. Os escritores dizem que um livro não pode ser finalizado, mas que pode ser descartado. O mesmo vale para a otimização do NS: o espaço dos hiperparâmetros é tão grande que a otimização não pode ser concluída, mas só pode ser interrompida, deixando o NS para os descendentes. Portanto, seu objetivo será desenvolver um fluxo de trabalho que permita executar rapidamente uma boa otimização, deixando a oportunidade de experimentar opções de otimização mais detalhadas, se necessário.

As dificuldades na seleção dos hiperparâmetros fazem com que algumas pessoas se queixem de que os SNs exigem muito esforço em comparação com outras técnicas de MO. Ouvi muitas variantes de reclamações como: “Sim, um NS bem ajustado pode oferecer a melhor eficiência na solução de um problema. Mas, por outro lado, eu posso tentar uma floresta aleatória [ou SVM, ou qualquer outra tecnologia favorita], e simplesmente funciona. Não tenho tempo para descobrir qual NA é a certa para mim. " Obviamente, do ponto de vista prático, é bom ter técnicas fáceis de usar com um amigo. Isso é especialmente bom quando você está apenas começando a trabalhar com uma tarefa e ainda não está claro se o MO pode ajudar a resolvê-la. Por outro lado, se é importante que você obtenha os melhores resultados, pode ser necessário experimentar várias abordagens que requerem conhecimento mais especializado. Seria ótimose MO sempre foi fácil, mas não há razões para que isso seja trivial a priori.

Outras técnicas

Cada uma das técnicas desenvolvidas neste capítulo é valiosa por si só, mas essa não é a única razão pela qual as descrevi. É mais importante se familiarizar com alguns dos problemas que podem surgir no campo de NA e com um estilo de análise que pode ajudar a superá-los. De certa forma, estamos aprendendo a pensar sobre o NS. No restante deste capítulo, descreverei brevemente um conjunto de outras técnicas. Suas descrições não serão tão profundas quanto as anteriores, mas devem transmitir algumas sensações sobre a variedade de técnicas encontradas no campo de NA.

Variações da descida do gradiente estocástico

A descida do gradiente estocástico por meio da retropropagação nos serviu bem durante o ataque ao problema de classificação de números manuscritos do MNIST. No entanto, existem muitas outras abordagens para otimizar a função de custo e, às vezes, mostram uma eficiência superior à da descida estocástica do gradiente com minipacotes. Nesta seção, descrevo brevemente duas dessas abordagens, Hessian e momentum.

Hessian

Para começar, vamos deixar de lado a Assembléia Nacional. Em vez disso, simplesmente consideramos o problema abstrato de minimizar a função de custo C de muitas variáveis, w = w1, w2, ..., ou seja, C = C (w). Pelo teorema de Taylor, a função de custo no ponto w pode ser aproximada:

$$

$$C(w+\Delta w) = C(w) + \sum_j \frac{\partial C}{\partial w_j} \Delta w_j \nonumber \\ + \frac{1}{2} \sum_{jk} \Delta w_j \frac{\partial^2 C}{\partial w_j \partial w_k} \Delta w_k + \ldots \tag{103}$$

Podemos reescrevê-lo de forma mais compacta como

$$

$$C(w+\Delta w) = C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w + \ldots \tag{104}$$

onde ∇C é o vetor gradiente comum e H é a matriz conhecida como matriz de Hessian , onde jk contém ∂ ² C / ∂w _j ∂w _k . Suponhamos que aproximamos C abandonando termos de ordem superior escondidos atrás das reticências na fórmula:

$$

$$C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w \tag{105}$$

Usando álgebra, pode ser mostrado que a expressão no lado direito pode ser minimizada selecionando:

$$

$$\Delta w = -H^{-1} \nabla C \tag{106}$$

Estritamente falando, para que isso seja apenas um mínimo, e não apenas um extremo, devemos assumir que a matriz hessiana é um positivo mais definido. Intuitivamente, isso significa que a função C é como um vale, não uma montanha ou uma sela.

Se (105) for uma boa aproximação à função de custo, espera-se que a transição do ponto w para o ponto w + Δw = w - H - 1 −C reduza significativamente a função de custo. Isso oferece um possível algoritmo de minimização de custos:

• Selecione o ponto inicial w.
• Atualize w para um novo ponto, w ′ = w - H ⁻¹ ∇C, onde o Hessian H e ∇C são calculados em w.
• w' , w′′=w′−H′ ⁻¹ ∇′C, H ∇C w'.
• ...

Na prática, (105) é apenas uma aproximação, e é melhor dar passos menores. Faremos isso atualizando constantemente w por Δw = −ηH - 1∇C, onde η é a velocidade de aprendizado.

Essa abordagem para minimizar a função de custo é conhecida como otimização de Hessian. Há resultados teóricos e empíricos mostrando que os métodos de Hessian convergem para o mínimo em menos etapas do que uma descida de gradiente padrão. Em particular, ao incluir informações sobre alterações de segunda ordem na função de custo, é possível evitar muitas patologias encontradas na descida do gradiente na abordagem de Hessian. Além disso, existem versões do algoritmo de retropropagação que podem ser usadas para calcular o Hessian.

Se a otimização do Hessian é tão legal, por que não a usamos em nosso NS? Infelizmente, embora tenha muitas propriedades desejáveis, há uma muito indesejável: é muito difícil colocar em prática. Parte do problema é o enorme tamanho da matriz hessiana. Suponha que tenhamos um NS com 10 ⁷ pesos e compensações. Então, na matriz hessiana correspondente, haverá 10 ⁷ × 10 ⁷ = 10 ¹⁴ elementos. Demais! Como resultado , acaba sendo muito difícil calcular H- ¹ ∇C na prática. Mas isso não significa que é inútil saber sobre ela. Muitas opções de descida de gradiente são inspiradas na otimização de Hessian, elas simplesmente evitam o problema de matrizes excessivamente grandes. Vamos dar uma olhada em uma dessas técnicas, a descida do gradiente de impulso.

Descida de gradiente baseada em impulso

Intuitivamente, a vantagem da otimização de Hessian é que ela inclui não apenas informações sobre o gradiente, mas também informações sobre suas alterações. A descida do gradiente baseada em impulso é baseada em uma intuição semelhante, mas evita matrizes grandes de segundas derivadas. Para entender a técnica de impulso, vamos relembrar nossa primeira imagem de descida gradiente, na qual examinamos uma bola rolando por um vale. Então vimos que a descida do gradiente, ao contrário do nome, se assemelha apenas ligeiramente a uma bola caindo no fundo. A técnica de pulso altera a descida do gradiente em dois lugares, o que a torna mais parecida com uma imagem física. Primeiro, ela introduz o conceito de "velocidade" para os parâmetros que estamos tentando otimizar. O gradiente está tentando alterar a velocidade, não o "local" diretamente, semelhante à forma como as forças físicas alteram a velocidade,e afetam apenas indiretamente o local. Em segundo lugar, o método de impulso é um tipo de termo de atrito que reduz gradualmente a velocidade.

Vamos dar uma definição mais matematicamente precisa. Introduzimos as variáveis ​​de velocidade v = v1, v2, ..., uma para cada variável correspondente w _j (na rede neural, essas variáveis ​​incluem naturalmente todos os pesos e deslocamentos). Em seguida, alteramos a regra de atualização da descida do gradiente w → w ′ = w - η∇C para

$$

$$v \rightarrow v' = \mu v - \eta \nabla C \tag{107}$$

$$

$$w \rightarrow w' = w+v' \tag{108}$$

Nas equações, μ é um hiperparâmetro que controla a quantidade de frenagem ou atrito do sistema. Para entender o significado das equações, primeiro é útil considerar o caso em que μ = 1, ou seja, quando não há atrito. Nesse caso, o estudo das equações mostra que agora a “força” ∇C altera a velocidade v, e a velocidade controla a taxa de variação w. Intuitivamente, é possível ganhar velocidade adicionando constantemente membros gradientes a ela. Isso significa que, se o gradiente se mover em aproximadamente uma direção durante várias etapas do treinamento, podemos obter uma velocidade de movimento suficientemente alta nessa direção. Imagine, por exemplo, o que acontece quando se move ladeira abaixo:



A cada passo da encosta, a velocidade aumenta e nos movemos cada vez mais rápido para o fundo do vale. Isso permite que a técnica de velocidade corra muito mais rápido que a descida de gradiente padrão. Obviamente, o problema é que, tendo atingido o fundo do vale, vamos passar por ele. Ou, se o gradiente mudar muito rapidamente, pode acontecer que estamos nos movendo na direção oposta. Este é o ponto de introduzir o hiperparâmetro μ em (107). Eu disse anteriormente que µ controla a quantidade de atrito no sistema; mais precisamente, a quantidade de atrito deve ser imaginada como 1 μ. Quando µ = 1, como vimos, não há atrito, e a velocidade é completamente determinada pelo gradiente ∇C. E vice-versa, quando μ = 0, há muito atrito, nenhuma velocidade é obtida e as equações (107) e (108) são reduzidas às equações usuais de descida do gradiente, w → w ′ = w - η∇C. Na prática,usar o valor de μ no intervalo entre 0 e 1 pode nos dar a vantagem da capacidade de ganhar velocidade sem o risco de escorregar no mínimo. Podemos escolher esse valor para μ usando os dados de confirmação pendentes da mesma maneira que escolhemos os valores para η e λ.

Até agora, evitei nomear o hiperparâmetro μ. O fato é que o nome padrão para μ foi mal escolhido: é chamado de coeficiente de momento. Isso pode ser confuso, porque µ não é nada parecido com o conceito de momento da física. Está muito mais fortemente associado ao atrito. No entanto, o termo “coeficiente de momentum” é amplamente usado, portanto continuaremos a usá-lo também.

Uma característica interessante da técnica de impulso é que quase nada precisa ser feito para alterar a implementação da descida do gradiente para incluir essa técnica nela. Ainda podemos usar a propagação reversa para calcular gradientes, como antes, e usar idéias como verificar minipacks estocásticos selecionados. Nesse caso, podemos obter alguns dos benefícios da otimização do Hessian usando informações sobre alterações de gradiente. No entanto, tudo isso acontece sem falhas e com apenas pequenas alterações no código. Na prática, a técnica de impulso é amplamente usada e geralmente ajuda a acelerar o aprendizado.

Exercícios

• O que vai dar errado se usarmos μ> 1 na técnica de pulso?
• O que vai dar errado se usarmos <0 na técnica de pulso?

Desafio

• Adicione a descida do gradiente estocástico com base no momento ao network2.py.

Outras abordagens para minimizar a função de custo

Muitas outras abordagens foram desenvolvidas para minimizar a função de custo e nenhum acordo foi alcançado sobre a melhor abordagem. Aprofundando o assunto das redes neurais, é útil se aprofundar em outras tecnologias, entender como elas funcionam, quais são seus pontos fortes e fracos e como colocá-las em prática. No trabalho que mencionei anteriormente , várias dessas técnicas são introduzidas e comparadas, incluindo a descida gradiente emparelhada e o método BFGS (e também estudamos o método BFGS estreitamente relacionado com limite de memória, ou L-BFGS ). Outra tecnologia que recentemente mostrou resultados promissores., esse é o gradiente acelerado de Nesterov, melhorando a técnica de pulso. No entanto, a descida simples do gradiente funciona bem para muitas tarefas, especialmente ao usar o momento, portanto, permaneceremos na descida estocástica do gradiente até o final do livro.

Outros modelos de neurônio artificial

Até agora, criamos nosso NS usando neurônios sigmóides. Em princípio, o NS construído em neurônios sigmóides pode calcular qualquer função. Mas, na prática, as redes construídas em outros modelos de neurônios às vezes estão à frente dos modelos sigmóides. Dependendo do aplicativo, as redes baseadas nesses modelos alternativos podem aprender mais rapidamente, generalizar melhor os dados de verificação ou fazer as duas coisas. Deixe-me mencionar alguns modelos alternativos de neurônios para ter uma idéia de algumas opções usadas com frequência.

Talvez a variação mais simples seja um neurônio tang que substitui uma função sigmóide por uma tangente hiperbólica. A saída de um neurônio tangente com a entrada x, um vetor de pesos w e um deslocamento b é especificada como

$$

$$\tanh(w \cdot x+b) \tag{109}$$

onde tanh é naturalmente tangente hiperbólica . Acontece que ele está intimamente ligado ao neurônio sigmóide. Para ver isso, lembre-se que tanh é definido como

$$

$$\tanh(z) \equiv \frac{e^z-e^{-z}}{e^z+e^{-z}} \tag{110}$$

Usando um pouco de álgebra, é fácil ver que

$$

$$\sigma(z) = \frac{1+\tanh(z/2)}{2} \tag{111}$$

isto é, tanh está apenas escalando o sigmóide. Graficamente, você também pode ver que a função tanh tem a mesma forma que o sigmóide: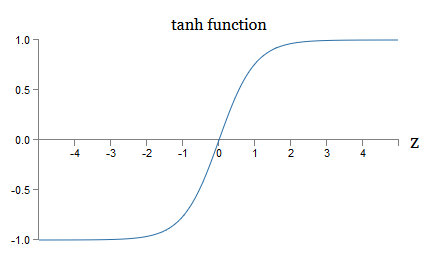



Uma diferença entre os neurônios tang e os neurônios sigmóides é que a saída do primeiro se estende de -1 a 1, e não de 0 a 1. Isso significa que, ao criar uma rede baseada em neurônios tangentes, talvez seja necessário normalizar suas saídas (e, dependendo dos detalhes do aplicativo, talvez as entradas) um pouco diferente das redes sigmóides.

Como os sigmóides, os neurônios tang, em princípio, podem calcular qualquer função (embora existam alguns truques), marcando entradas de -1 a 1. Além disso, as idéias de propagação traseira e descida de gradiente estocástico são igualmente fáceis de aplicar ao tang -neurônios, bem como sigmóides.

Exercício

• Prove a equação (111).

Que tipo de neurônio deve ser usado em redes, tang ou sigmóide? A resposta, para dizer o mínimo, não é óbvia! No entanto, existem argumentos teóricos e algumas evidências empíricas de que os neurônios tangores às vezes funcionam melhor. Vamos analisar brevemente um dos argumentos teóricos a favor dos neurônios tang. Suponha que usemos neurônios sigmóides, e todas as ativações na rede serão positivas. Considere os pesos w ^{l + 1} _jk incluídos para o neurônio n. J na camada n. L + 1. regras Back-Propagation (Bp4) dizem-nos que o gradiente associado é um ^l _{a k} delta ^{l + 1,} _j . Como as ativações são positivas, o sinal desse gradiente será o mesmo de δ ^{l + 1} _j. Isso significa que se δ ^{l + 1} _{j for} positivo, todos os pesos w ^{l + 1} _jk diminuirão durante a descida do gradiente e se δ ^{l + 1} _{j for} negativo, todos os pesos w ^{l + 1} _jkaumentará durante a descida do gradiente. Em outras palavras, todos os pesos associados ao mesmo neurônio aumentam ou diminuem juntos. E isso é um problema, porque você pode precisar aumentar alguns pesos enquanto reduz outros. Mas isso pode acontecer apenas se algumas ativações de entrada tiverem sinais diferentes. Isso sugere a necessidade de substituir o sigmóide por outra função de ativação, por exemplo, tangente hiperbólica, que permite que as ativações sejam positivas e negativas. De fato, como tanh é simétrico em relação a zero, tanh (−z) = −tanh (z), pode-se esperar que, grosso modo, as ativações em camadas ocultas sejam igualmente distribuídas entre positivo e negativo. Isso ajudará a garantir que não haja viés sistemático nas atualizações das escalas em uma direção ou outra.

Quão seriamente esse argumento deve ser considerado? Afinal, é heurístico, não fornece evidências estritas de que os neurônios tang são superiores aos sigmóides. Talvez os neurônios sigmóides possuam algumas propriedades que compensem esse problema? De fato, em muitos casos, a função tanh mostrou vantagens mínimas a inexistentes em comparação com o sigmóide. Infelizmente, não temos métodos simples e implementados rapidamente para verificar qual tipo de neurônio aprenderá mais rapidamente ou se mostrará mais eficaz na generalização de um caso específico.

Outra variante de um neurônio sigmóide é um neurônio linear retificado, ou unidade linear retificada, ReLU. A saída ReLU com entrada x, o vetor de pesos we deslocamento b é especificado da seguinte forma:

$$

$$\max(0, w \cdot x+b) \tag{112}$$

A função de correção gráfica max (0, z) é assim:



Esses neurônios, obviamente, são muito diferentes dos neurônios sigmoides e tang. No entanto, eles são semelhantes, pois também podem ser usados ​​para calcular qualquer função e podem ser treinados usando propagação de retorno e descida de gradiente estocástico.

Quando devo usar ReLU em vez de neurônios sigmóides ou tang? Em trabalhos recentes sobre reconhecimento de imagem ( 1 , 2 , 3 , 4) Foram encontradas sérias vantagens de usar o ReLU em quase toda a rede. No entanto, como nos neurônios tang, ainda não temos uma compreensão realmente profunda de quando exatamente quais ReLUs serão preferíveis e por quê. Para ter uma idéia de alguns problemas, lembre-se de que os neurônios sigmóides param de aprender quando saturados, ou seja, quando a saída é próxima de 0 ou 1. Como vimos muitas vezes neste capítulo, o problema é que os membros de σ reduzem o gradiente isso atrasa o aprendizado. Os neurônios Tang sofrem de dificuldades semelhantes na saturação. Ao mesmo tempo, um aumento na entrada ponderada na ReLU nunca a saturará, portanto, uma desaceleração correspondente no treinamento não ocorrerá. Por outro lado, quando a entrada ponderada na ReLU é negativa, o gradiente desaparece e o neurônio deixa de aprender.Este é apenas um dos muitos problemas que tornam pouco trivial entender quando e como as ReLUs se comportam melhor do que os neurônios sigmóides ou tang.

Eu pintei um quadro de incerteza, enfatizando que ainda não temos uma teoria sólida da escolha das funções de ativação. De fato, esse problema é ainda mais complicado do que eu descrevi, uma vez que existem infinitas funções de ativação possíveis. Qual deles nos dará a rede de aprendizado mais rápido? Qual dará a maior precisão nos testes? Estou surpreso com o número de estudos realmente aprofundados e sistemáticos sobre essas questões. Idealmente, devemos ter uma teoria que nos diga em detalhes como escolher (e possivelmente mudar rapidamente) nossas funções de ativação. Por outro lado, não devemos ser impedidos pela falta de uma teoria completa! Já temos ferramentas poderosas e, com a ajuda deles, podemos alcançar um progresso significativo. Até o final do livro, usarei os neurônios sigmóides como os principais,pois eles funcionam bem e dão ilustrações concretas de idéias-chave relacionadas à Assembléia Nacional. Mas lembre-se de que as mesmas idéias podem ser aplicadas a outros neurônios, e essas opções têm suas vantagens.

: , , ? ?

: , . , . . : , , ?

—

Uma vez em uma conferência sobre o básico da mecânica quântica, notei o que parecia ser um hábito engraçado da fala: no final do relatório, as perguntas da platéia geralmente começavam com a frase: "Eu realmente gosto do seu ponto de vista, mas ..." Os fundamentos quânticos não são exatamente o meu campo usual, e chamei a atenção para esse estilo de fazer perguntas, porque em outras conferências científicas eu praticamente não encontrei para que o questionador demonstrasse simpatia pelo ponto de vista do orador. Naquela época, decidi que a prevalência de tais questões indicava que o progresso nos fundamentos quânticos era bastante alcançado e que as pessoas estavam apenas começando a ganhar impulso. Mais tarde, percebi que essa avaliação era muito dura. Os oradores lutaram com alguns dos problemas mais difíceis que as mentes humanas já encontraram. Naturalmente, o progresso foi lento!No entanto, ainda havia valor em ouvir notícias do pensamento das pessoas sobre essa área, mesmo que elas tivessem pouco ou nada.

Neste livro, você deve ter notado um "tique nervoso" semelhante à frase "Estou muito impressionado". Para explicar o que temos, recorri frequentemente a palavras como "heuristicamente" ou "grosso modo", seguidas de uma explicação de um fenômeno em particular. Essas histórias são críveis, mas as evidências empíricas eram muitas vezes bastante superficiais. Se você estudar a literatura de pesquisa, verá que histórias desse tipo aparecem em muitos trabalhos de pesquisa em redes neurais, geralmente na companhia de uma pequena quantidade de evidências que as apóiam. Como nos relacionamos com essas histórias?

Em muitos campos da ciência - especialmente onde fenômenos simples são considerados - é possível encontrar evidências muito rigorosas e confiáveis ​​de hipóteses muito gerais. Mas na Assembléia Nacional há um grande número de parâmetros e hiperparâmetros, e há relações extremamente complexas entre eles. Em sistemas incrivelmente complexos, é incrivelmente difícil fazer declarações gerais confiáveis. A compreensão do NS em toda a sua plenitude, como fundamentos quânticos, testa os limites da mente humana. Freqüentemente, temos que dispensar evidências a favor ou contra vários casos específicos específicos de uma declaração geral. Como resultado, algumas vezes essas declarações precisam ser alteradas ou abandonadas, à medida que novas evidências surgem.

Uma das abordagens para essa situação é considerar que qualquer história heurística sobre o SN implica em um certo desafio. Por exemplo, considere a explicação que citei sobre por que uma exceção (abandono) do trabalho em 2012 funciona.: “Essa técnica reduz a complexa adaptação articular dos neurônios, já que um neurônio não pode contar com a presença de certos vizinhos. No final, ele precisa aprender características mais confiáveis ​​que possam ser úteis no trabalho em conjunto com muitos subconjuntos aleatórios diferentes de neurônios. ” Uma declaração rica e provocativa, com base na qual você pode construir um programa de pesquisa completo, no qual precisará descobrir o que é verdadeiro, onde está errado e o que precisa ser esclarecido e alterado. E agora realmente existe uma indústria inteira de pesquisadores estudando a exceção (e suas muitas variações), tentando entender como ela funciona e quais limitações ela possui. Assim é com muitas outras abordagens heurísticas que discutimos. Cada um deles não é apenas uma explicação potencial,mas também um desafio para a pesquisa e um entendimento mais detalhado.

Obviamente, nenhuma pessoa terá tempo suficiente para investigar todas essas explicações heurísticas profundamente. Toda a comunidade de pesquisadores de NS levará décadas para desenvolver uma teoria realmente poderosa do treinamento em NS com base em evidências. Isso significa que vale a pena rejeitar as explicações heurísticas como frouxas e sem evidências? Não! Precisamos de uma heurística que inspire nosso pensamento. Isso é semelhante à era das grandes descobertas geográficas: os primeiros estudiosos frequentemente agiam (e faziam descobertas) com base em crenças que eram equivocadas de maneira séria. Mais tarde, corrigimos esses erros, reabastecendo nosso conhecimento geográfico. Quando você entende algo mal - como os pesquisadores entendem a geografia e como hoje entendemos o NS - é mais importante estudar corajosamente o desconhecido,do que estar escrupulosamente certo a cada passo do seu raciocínio. Portanto, você deve considerar essas histórias como instruções úteis sobre como refletir sobre os NSs, mantendo uma consciência saudável de suas limitações e monitorando cuidadosamente a confiabilidade das evidências em cada caso. Em outras palavras, precisamos de boas histórias para motivação e inspiração e investigações minuciosas e escrupulosas para revelar fatos reais.