Eu vim para o mundo da TI pela física teórica. Ele estava envolvido principalmente em tarefas econômicas. Envolvido - isto: análise, TK, declaração, design, programação. Naturalmente, comparei o tempo todo as abordagens físicas e econômicas para entender as leis da natureza e da economia, respectivamente. Um certo ponto de vista amadureceu sobre esse assunto. Sobre ela e será discutido.
1. Sobre a cognição em geral
Existem duas abordagens para a cognição:
A abordagem de Aristóteles . Essa é uma abordagem holística e trata o objeto como uma caixa preta. O fenômeno, o objeto é estudado em toda a realidade como um todo. E a realidade diz, por exemplo, que corpos pesados caem no chão mais rápido que os leves; que deixou para si um corpo em movimento para gradualmente. A abordagem de Aristóteles lida com o fenômeno como uma realidade integral, portanto, pode ser chamado de fenomenológico.
Abordagem de Galileu . Esta é uma abordagem analítica de sistemas. Essa é a abordagem de dividir e conquistar. O fenômeno, o objeto é decomposto em suas partes constituintes e cada uma delas é estudada separadamente, abstraindo do resto (análise). Em seguida, as imagens resultantes podem ser combinadas em uma, levando em consideração a interação dos componentes (síntese). Por exemplo, a queda de corpos é considerada como a queda de corpos no vazio. E aí eles acabam caindo com a mesma aceleração. Mas, na realidade, o atrito contra o ar os impede de cair igualmente. Tendo estudado essa força separadamente, podemos explicar o resultado de Aristóteles. Da mesma forma, se nos libertarmos das forças de atrito, o corpo em movimento se moverá sem parar. E se levarmos em conta a força de atrito, obtemos o resultado de Aristóteles. A abordagem de Galileu leva imediatamente à necessidade de estudar forças. No final, isso se traduz em um sistema coerente da física clássica.
Mais uma vez, para maior clareza.
A abordagem de Aristóteles . Há um fenômeno em estudo: “A queda de um corpo no ar no chão” - o fenômeno F. Nós pegamos corpos diferentes e descobrimos que corpos mais pesados caem no chão mais rápido que os leves.
Abordagem de Galileu . Ao estudar o fenômeno de F, deve-se levar em conta não apenas o peso. Estudamos a queda no ar. E vamos mudar não apenas o peso, mas também o ar. Vamos tentar reduzir sua densidade, para que, no final, não exista ar. Então descobrimos que todos os corpos caem no vazio com a mesma aceleração. Encontramos os parâmetros de influência sobre o fenômeno e tentamos criar condições sob as quais apenas um parâmetro é significativo. Isso não está na natureza. Portanto, um físico precisa de um laboratório onde ele possa variar os parâmetros. Tendo estudado a influência de um parâmetro, podemos continuar estudando a influência de outro parâmetro. Estamos tentando reduzir a complexidade de toda a abordagem à composição de abordagens mais simples. Variando a forma do corpo em queda, podemos estudar a dependência da força de atrito no ar, dependendo da forma do corpo. Variando a taxa de queda, podemos detectar a dependência da força de atrito na velocidade. Variando a altura da queda, podemos detectar a dependência da aceleração na altura. Ao variar a localização geográfica da Terra, encontramos a dependência da aceleração da queda na geografia.
Grosso modo, na abordagem de Aristóteles eles estudam a realidade, e na abordagem de Galileu estudam abstrações e, a partir delas, através da síntese, vão para a realidade.
2. O modelo do conhecimento físico
A física é uma teoria ideal para muitas ciências, incluindo a economia. Em experimentos físicos, séries discretas de valores são obtidas. Mas eles são considerados uma aproximação a funções contínuas, que na realidade são indicadores físicos. E os físicos estão tentando adivinhar essas funções. Então Galileu adivinhou a parábola para a trajetória de uma pedra lançada em ângulo com o horizonte; Kepler adivinhou as trajetórias dos planetas - elipses, etc. Depois de adivinhar a trajetória, obtemos um aparato preditivo - a capacidade de calcular o valor para coordenadas inexploradas da trajetória. Para testar, eles colocaram um experimento - crie as condições para a obtenção experimental do valor do interesse. Depois de verificar o valor previsto e o experimental, obtemos confirmação ou refutação da teoria. Aqui, às vezes, o erro do erro experimental desempenha um papel importante. O conhecimento físico se resume à identificação do determinismo - a lei de obter um estado de um estado inicial:
S(0) - D – – , S(t) S(0) Q – . , , .
Então, para uma pedra jogada de um ponto (0,0) com uma velocidade em um ângulo para o horizonte que temos
$$ display $$ x (t) = v_0 t cos (α), y (t) = v_0 t sin (α) - (gt ^ 2) / 2 $$ display $$
O estado inicial S (0) é definido por três parâmetros: ponto de partida (0,0), velocidade inicial ângulo .
O impacto do ambiente Q é dado pela aceleração da gravidade g. Ao expandir o escopo do problema (alta velocidade inicial) g não é mais constante.
O determinismo D é dado pela fórmula acima.
Para uma tarefa mais realista, o atrito contra o ar deve ser levado em consideração. Isso complica a matemática do problema, mas o princípio permanece o mesmo. Em vez de pedra, você pode considerar um avião. Em seguida, a força de impulso da aeronave entra em jogo e sua regulamentação pelo piloto. Um fator não físico também aparece - a vontade do piloto. Não podemos levar isso em conta. Mas sabemos que não é ilimitado: a tração não pode ser infinita, a aceleração não pode ser infinita. Isso introduz um elemento de certeza no movimento. Eles usam, por exemplo, para construir a trajetória de um míssil de defesa aérea.
Vamos voltar para a pedra voadora. É caracterizada por um número infinito de parâmetros físicos. Por exemplo, apenas sua forma pode ser arbitrariamente complexa. Mas temos certeza de que em alguma área útil podemos considerar a pedra como um ponto material. Esta é a principal abstração da mecânica clássica. Todos os sistemas são representados como conjuntos de pontos de material em interação. Isso faz a principal redução cognitiva - reduzindo o comportamento de um sistema complexo ao comportamento de seus componentes elementares.
Em conexão com a redução cognitiva mencionada, duas abordagens epistemológicas podem ser distinguidas - reducionismo e holismo.
3. Reducionismo e holismo
O reducionismo é o princípio de reduzir as características de um sistema das características dos subsistemas e das características da interação dos subsistemas. Trabalha com sucesso em física.
Considere, por exemplo, gás. Sem decompô-lo em subsistemas, podemos operar com conceitos fenomenológicos experimentais: pressão P, temperatura T, volume V. Empiricamente, encontramos a relação que liga esses parâmetros - a equação de estado do gás:
Este é o chamado nível fenomenológico - trabalhe com fenômenos (fenômenos) sem entrar em sua estrutura. Essa é a abordagem de Aristóteles.
Agora aplique a abordagem do Galileo. Decompomos o sistema "gás": imagine-o como uma coleção de moléculas em colisão. Em seguida, definimos P e T através dos parâmetros mecânicos da molécula. Isso é feito na física molecular. Assim, reduzimos o sistema de gás a subsistemas de moléculas. Isso esclarecerá a equação de estado ou a deduzirá para novos sistemas.
Assim, nos negócios, temos uma analogia: a macroeconomia é decomposta em empresas e residências. Mas aqui a redução ainda não é perfeita. Infelizmente, não há Newton econômico. O problema é a complexidade e a disponibilidade de um fator subjetivo que não está na física (embora exista um debate sobre o papel do sujeito na mecânica quântica).
E agora sobre holismo.
Holismo é o princípio de que pode haver propriedades não redutíveis em um sistema. Assim, na biologia, a doutrina do vitalismo é baseada no conceito de enteléquia, a força da vida inerente ao corpo como um todo e irredutível.
Até agora, a física dispensa o conceito de holismo.
Um modelo de fórmula é um modelo definido por uma fórmula. O conceito de "fórmula" será considerado conhecido.
Exemplos em física: equações de Newton, equações de Lagrange, equações de Maxwell, equações de Navier-Stokes, equações de Heisenberg-Schrödinger, equações de Einstein.
Exemplos da economia: fórmula de Black-Scholes para o preço da opção, fórmula de oferta de moeda, modelo de programação linear para otimizar o portfólio financeiro, fórmulas de cálculo de juros, fórmulas de cálculo de risco.
Com um modelo de fórmula, uma pessoa pode trabalhar sem um computador. Tal é quase toda matemática pura. Mas aqui, o algoritmo desempenha um papel cada vez mais importante. Portanto, a solução para o problema de quatro cores não foi reduzida a alguma fórmula, mas exigiu uma solução de força bruta para muitos casos especiais. Esse busto foi feito por computadores.
Modelo algorítmico - um modelo definido por um algoritmo, possivelmente não redutível a uma fórmula. Obviamente, é possível classificar o algoritmo como fórmulas, mas essas não são as mesmas fórmulas clássicas. O modelo algorítmico é inicialmente realista apenas usando um computador
Um modelo formal sempre pode ser reduzido a um algoritmo.
Um exemplo do primeiro modelo algorítmico é o problema de Fermi-Pasta-Ulam. Aqui está uma citação do livro de Ulam, The Adventures of Mathematics.
CitaçãoAssim que as máquinas foram concluídas, Fermi, com sua intuição e grande senso comum, percebeu imediatamente toda a sua importância no estudo de problemas da física teórica, astrofísica e física clássica. Discutimos essa questão da maneira mais detalhada e decidimos tentar formular algum problema que seria simples em sua formulação, mas teria uma solução que exigia cálculos muito longos, impossíveis com a ajuda de caneta e papel ou dispositivos de computação mecânica existentes. Depois de discutir uma série de possíveis problemas, resolvemos um problema típico relacionado ao comportamento de longo prazo de um sistema dinâmico e exigindo uma previsão de longo prazo. Considerou uma corda elástica com duas extremidades fixas, afetada não apenas pela força de deformação elástica usual proporcional à deformação, mas também por uma pequena força física não linear. Foi necessário descobrir como, após um número muito grande de períodos de oscilação, essa não linearidade afetará gradualmente o comportamento periódico conhecido das oscilações em uma chave, como outras chaves adquirirão suas amplitudes e como, argumentamos, o movimento será termizado, imitando, talvez, o comportamento líquidos, que, sendo inicialmente laminares, tornam-se cada vez mais turbulentos, até que, finalmente, seu movimento macroscópico é convertido em calor.
John Pasta, um físico que chegou recentemente a Los Alamos, nos ajudou a criar fluxogramas, programação e tarefas de processamento no MANIAC. Fermi decidiu aprender a programar uma máquina. Naquela época, era mais difícil do que agora, quando já existem programas prontos e regras estabelecidas, e esse procedimento em si é automatizado. Então foi necessário aprender vários truques. Fermi os dominou muito rapidamente e me ensinou algo, embora eu já soubesse o suficiente para avaliar que tipo de tarefas podem ser resolvidas dessa maneira, determinar sua duração no número de etapas de cálculo e entender os princípios de sua implementação.
Como se viu, selecionamos a tarefa com muito sucesso. Os resultados obtidos em termos qualitativos diferiam completamente mesmo daqueles que Fermi esperava com seu conhecimento mais profundo dos movimentos das ondas. O objetivo inicial era ver a que velocidade a energia da corda, originalmente incorporada em uma onda sinusoidal simples (uma nota era tomada como um tom), criaria gradualmente harmônicos mais altos e como o sistema chegaria a um estado caótico final, descrevendo como o formato da corda , portanto, a natureza da distribuição de energia entre chaves cada vez mais altas. Mas nada disso aconteceu. Para nossa surpresa, a corda começou a tocar apenas em algumas notas surdas e, o que é provavelmente ainda mais surpreendente, depois de várias centenas de vibrações alternativas comuns, novamente assumiu quase a mesma forma sinusoidal do início.
Eu sei que Fermi considerou isso uma "pequena descoberta", como ele mesmo disse. Mas ele iria contar sobre ele um ano depois, quando foi convidado para dar uma palestra por Gibbs (um evento muito honroso na reunião anual da American Mathematics Society). Ele ficou doente antes da reunião, e essa palestra nunca ocorreu. No entanto, um relatório sobre este trabalho, escrito por Fermi, Pasta e eu, foi, no entanto, publicado - como um relatório sobre o trabalho em Los Alamos.
Devo explicar que o movimento de um meio contínuo, como uma corda, por exemplo, pode ser estudado usando um computador, se imaginarmos que uma corda consiste em um número finito de partículas - no nosso caso, sessenta e quatro ou cento e vinte e oito. (O número de elementos é melhor representado como uma potência de dois, pois facilita o processamento em um computador.) Essas partículas são ligadas por forças que, além de termos lineares de distância, também contêm pequenos termos quadráticos não lineares. Em seguida, a máquina calcula rapidamente o movimento de cada um desses pontos em etapas curtas. Tendo calculado uma posição, ela vai para outro estágio de tempo e calcula uma nova posição, e assim se repete muitas vezes. Não há absolutamente nenhuma maneira de fazer esse cálculo manualmente, isso levaria literalmente milhares de anos. A solução em uma forma analítica usando métodos matemáticos da análise clássica dos séculos XIX e XX é completamente inaceitável aqui.
Os resultados foram realmente surpreendentes. Muitas tentativas foram feitas para elucidar as causas desse comportamento periódico e regular, que se tornou uma fonte para a literatura volumosa sobre oscilações não lineares existentes hoje. O trabalho neles foi escrito por Martin Kruskal, físico de Princeton, e Norman Zabuski, matemático que trabalhava no Bell Telephone Laboratory. Mais tarde, Peter Lake fez sua brilhante contribuição a essa teoria. Todos eles fizeram uma análise interessante de problemas desse tipo. O matemático sabe que o chamado sistema dinâmico de retorno de Poincaré, que inclui tantas partículas, tem um comprimento gigantesco - de fato, em escala astronômica - e que ele retorna rapidamente à sua posição original é mais surpreendente.
Outro físico de Los Alamos, James So, decidiu ver se o período que se segue a esse retorno muito próximo à posição inicial recomeça do mesmo estado e o que acontecerá após esse segundo "período". Juntamente com Pasta e Metropolis, ele repetiu todo o procedimento e, surpreendentemente, o retorno ocorreu novamente, mas com uma precisão inferior a cerca de um por cento. Essa imagem foi repetida ainda mais, mas após seis ou doze desses períodos, a precisão começou a aumentar novamente, o que indicava o aparecimento de um certo "super período". Então, uma estranheza foi seguida por outra, nada menos.
E aqui está um artigo sobre Habré que fala sobre o estado atual do problema Fermi-Pasta-Ulam:
Matemáticos resolveram o problema de Fermi-Pasta-Ulam
5. Coordenação
Por coordenação do sistema, quero dizer a definição de parâmetros básicos que, em princípio, determinam a evolução do sistema. Por exemplo, na mecânica de um ponto material, as coordenadas são definidas:
- Força externa F
- Massa m ponto de material
- Coordenadas espaciais (x, y, z) = r do ponto do material
- Tempo t
A evolução do sistema é dada pela equação de Newton
Qual é a coordenação da entidade econômica? Uma vez trabalhei em um sistema de inteligência de negócios. Seu principal termo é indicador. A base do sistema é um scorecard. Centenas de indicadores. Mas procurei em vão na Internet uma descrição da base dos indicadores - um conjunto de indicadores que não podem ser reduzidos a outros e que, em princípio, determinam completamente a evolução de uma entidade econômica. Ou seja, pelo que entendi, nenhuma coordenação foi feita na economia. E, portanto, falar sobre alguma lei dinâmica básica ainda não é possível. Só é possível, com base na conexão de indicadores, conduzir uma análise de cenário - responder à pergunta "O que acontecerá com os indicadores derivados se os indicadores subjacentes mudarem de acordo com o cenário fornecido?"
6. Exemplo abstrato. Previsão de séries temporais como física
Você pode perguntar o problema de previsão com base na série temporal real: com vários valores reais, é necessário obter o valor previsto do indicador - o valor no futuro. Isso implica um tipo de determinismo oculto da série temporal. Havia muitas especulações científicas e pseudocientíficas sobre esse assunto. Eu próprio lidei com médicos de ciências que alegavam que sua metodologia lhes permitiria obter uma previsão da taxa de câmbio e mostravam as dissertações correspondentes com todos os tipos de intervalos de confiança e outros atributos das leis de distribuição. Mas, quando confrontadas com a realidade, as técnicas foram destruídas.
Às vezes, para obter uma previsão, faça o seguinte:
- Veja a série temporal real {V (ti)}. Agenda - passo quebrado.
- Tome uma função contínua W (t) tal que W (ti) = V (ti). O gráfico é uma curva contínua.
- Um polinômio P (t) é selecionado que se aproxima de W (t) com um grau de precisão suficiente. Um polinômio pode ser considerado para todos os t.
- Então temos uma previsão para o tempo futuro T: V (T) = P (T)
Tudo isso dá a impressão de ciência, mas apenas à primeira vista. Sim, a existência de um polinômio aproximado para W (t) é garantida pelo teorema de Weierstrass da análise analítica. Podemos polinomizar arbitrariamente precisamente W (t). Mas não pode ser usado para previsões.
O valor aproximado para a série real é 100% e o valor preditivo é zero. Os polinômios podem ser inventados arbitrariamente, mas todos fornecerão previsões diferentes.
Quando o dia T chega e descobrimos o V (T) real, então para as séries {{V (ti)}, V (T)} podemos construir um novo polinômio Q (t) que se aproxima arbitrariamente dessa série com precisão, mas o tempo T não está mais em o futuro e Q (T) não são mais uma previsão, mas uma realidade. Os polinômios P (t) e Q (t) absolutamente não precisam coincidir e, para o novo tempo de previsão T '> T, eles mostrarão resultados diferentes. Ou seja, não há previsão. Parece haver ciência, mas nenhuma previsão. É como uma teoria medieval dos anjos. Ela pode explicar tudo, mas não pode prever nada.
A diferença entre interpolação física e extrapolação de econômica:
- A precisão dos dados empíricos : aproximada em física, exata em economia
- Funções de domínio : contínuo em física, descontínuo, gradual em economia
- Dados empíricos : em física, discretos, em economia contínua, com descontinuidades discretas
- Leis básicas : lá na física. F = ma, por exemplo; na economia ainda
7. Economia e física
Na economia, trajetórias reais - essencialmente descontínuas - são funções constantes por partes. Por exemplo, o indicador "Taxa de câmbio" pode dar um salto a qualquer momento. Funções econômicas contínuas - aproximações para fins de análise (se você tiver um martelo em suas mãos, deverá considerar qualquer objeto como um prego ...). Cada transação contábil causa saltos nos valores dos indicadores de derivativos de contas. E eles são a maioria dos indicadores. Além disso, cada mudança no número de trabalhadores é discreta, etc. A continuidade das trajetórias econômicas contrasta com a continuidade da maioria das trajetórias físicas. Portanto, o aparato da análise analítica não é diretamente aplicável às trajetórias econômicas.
Imagem para cognição física. A trajetória de uma pedra lançada em ângulo com o horizonte 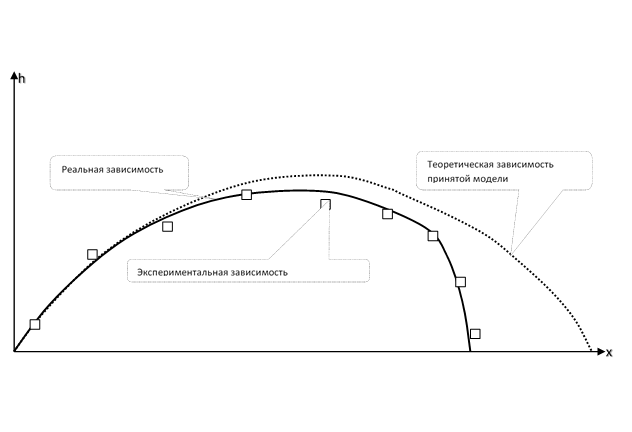
Imagem para conhecimento econômico. Taxa de câmbio no banco central.

Esta é uma função exata experimental real. É descontínuo nos momentos em que a taxa de câmbio muda.
Em física:
- Valores físicos experimentais são quase sempre aproximados
- Valores físicos experimentais formam uma série discreta.
- Uma série experimental discreta é considerada um polígono para aproximação contínua porque a realidade é contínua. A noção de continuidade pode vir a ser uma mentira em pequenas escalas espaciais e temporais. Então a física mudará de cara.
- Indicadores de linha de base bem definidos
- Trajetórias teóricas e reais são quase sempre contínuas e quase sempre diferenciáveis (a trajetória de um ponto material é sempre duas vezes diferenciável no tempo)
- Devido à continuidade da dinâmica real e à trajetória real, sua boa aproximação contínua tem poder preditivo: em uma vizinhança suficientemente pequena, a função não vai muito longe de seu último valor real.
Na economia:
- Valores econômicos experimentais podem ser considerados precisos. Somente na macroeconomia há um problema de precisão devido ao grande número de entidades comerciais.
- Valores econômicos experimentais consistem em intervalos de constância, interrompidos em determinados momentos no tempo em que o valor muda abruptamente
- Dados experimentais não podem ser considerados um campo de teste para aproximação contínua, porque a realidade é descontínua.
- Indicadores de linha de base não totalmente definidos. Não está claro por que dançar.
- Devido à descontinuidade da trajetória real, qualquer aproximação contínua arbitrariamente boa não garante previsões em nenhum bairro arbitrariamente pequeno.
- As trajetórias reais são quase sempre descontínuas. Isso significa que a determinação econômica requer uma abordagem diferente da mecânica clássica.
- Na economia, existe inicialmente um fator de livre arbítrio de uma entidade econômica. Seu alcance é regulado pelo estado. Os limites extremos dessa liberdade:
- Liberdade total em um mercado não estatal
- Liberdade parcial num mercado parcialmente regulamentado pelo Estado
- Completa falta de liberdade em um estado totalmente centralizado, onde não há mercado livre
O conhecimento econômico não atingiu um nível semelhante à mecânica clássica:
- Os componentes elementares do tipo de ponto de material não estão definidos
- Não definido Q (parâmetros ambientais), não está claro o que é importante, o que não é importante,
- ,
- ; .
. – . – . ? , . . . . , – .
, . , , - .
8. IT
8.1.
. . . . , . . . . . . . , , . . … , . . , . . . , . . . . . . . . . . . – " . - "!? , . -1840( , ). . . , . , . , . , . . , , . (). . , , , : ", . ". ! . , , - .
8.2. -
. — . , , .. . . , . . – . , . , . – . . …
. . , . , , , . , . . . . . , - . . . . , : , . . . , , . . ? . . , .
. - , .
, , . , . . , .
. . . , . , . , : , . , . . .
, – Jump Processing. , . .
, . “ ”. , – . , , . – , . . , – .
8.3.
( ). . “”. . , . , . . – . . , . . . . , . . – . . , . … . ? , . , - . . . , . , , . . .
. , . , . , – . , . , – ( – ?).
8.4.
“ ”
. () . . . , , . . , . . , , . . . – . , , . , . . , . Nice. . – . , . – . . , (, ). , . . , . . , , , . . . – . . . . . . . . . : , , , , , , , , … . 100 . ( , , ) . , ( , (SQL-) ). , . I.e. . . . , . . , : ”, . . . ”.
. , . , . : . , , .
. . . , , . . . . -.
() . , , ( ), . , . , – . , , , , , . . . , , . , “” “”. , “” “”. ? , .
: . . . , . . . . — . . : . : , …
. . , . . .
, . . - . . — . Por que isso? .
: IT. .