Prosseguimos com o cálculo das funções lógicas de acordo com o gráfico para uma classe mais ampla de comportamentos. Consideramos comportamentos autônomos cíclicos que não contêm múltiplos sinais (ou de outra maneira: não contêm eventos indexados). Outra limitação: por conveniência, não consideraremos a conexão de ramificações paralelas em OR. Consideramos apenas uma conexão por AND, ou seja, um evento é acionado apenas quando todos os seus eventos predecessores são acionados.
Usaremos o STG para descrever o comportamento, mas com restrições adicionais. Para cada local, o número de arcos entrando e saindo é estritamente igual a um cada. Assim, um local com arcos de entrada e saída pode ser considerado como um arco conectando dois eventos (transições). Consequentemente, a marcação se move ao longo dos arcos. Como comportamentos com vários sinais não são considerados agora, os índices de eventos são proibidos e não são necessários. Eventos vazios são proibidos. A situação também é proibida quando dois arcos incluídos em um evento saem de eventos que não são paralelos entre si (um caso especial é do mesmo evento). O objetivo disso é livrar-se de arcos que não carregam uma carga semântica. O restante é considerado correto (normal, ativo, seguro) do ponto de vista do comportamento do STG, levando em consideração as limitações acima. O comportamento não contém conflitos de CSC.
Definição 1. O evento no qual o arco entra é uma consequência do evento do qual esse arco sai. Por outro lado, o evento do qual o arco sai é a causa do evento no qual esse arco entra.
Definição 2. Um caminho - uma sequência interminável de eventos - resultado de alterações na rotulagem de um gráfico, começando com um específico. Cada evento entra na sequência um número infinito de vezes. Cada entrada é única.
Definição 3. O rastreio do evento A é o caminho no qual todos os eventos são conseqüência direta do evento A ou o resultado do fechamento transitivo do relacionamento da conseqüência dos eventos em relação ao evento A. A marcação inicial para o rastreio do evento A é estabelecida da seguinte forma. Se a marcação for alterada arbitrariamente, depois que o evento A for acionado, os marcadores nos arcos de saída do evento A serão corrigidos. Em seguida, o restante dos marcadores se move até que o movimento dos marcadores se torne impossível sem liberar os marcadores nos arcos de saída do evento A. A marcação resultante é a marcação inicial para o rastreamento do evento A.
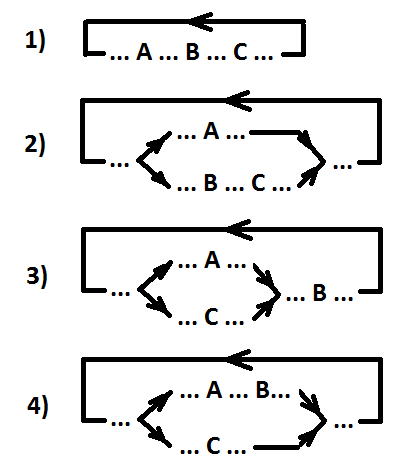
Definição 4. Introduzimos a relação de ordenação para três eventos (A, B, C). Três eventos são ordenados (escritos A> B> C) se e somente se, para qualquer rastreio do evento A, a primeira ocorrência do evento B na sequência sempre ocorrerá antes da primeira ocorrência do evento C.
Observação. O evento A pode ser paralelo aos eventos B e C (ou apenas C), ou ambos os eventos A e B podem ser paralelos ao evento C.
Opções de localização para eventos ordenados A, B e C (A> B> C).
Definição 5. O sinal b (comutação B1 e B2) capta o sinal a (comutação A1 e A2) em relação aos eventos X e Y (os eventos X e Y são paralelos ou coincidem) se as seguintes condições forem atendidas:
1) X> A1> A2;
2) se o evento A2 for paralelo ao evento X e não paralelo ao evento Y, então X> A2> Y;
3) Y> B1> B2;
4) se o evento B2 for paralelo ao evento Y e não paralelo ao evento X, então Y> B2> X;
5) Y> B1> A2;
6) se o evento A2 for paralelo ao evento Y e não paralelo ao evento X, Y> A2> X.
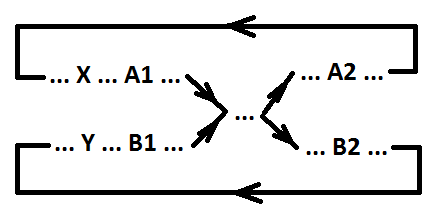
Observação 1. As condições 1, 2 e 3, 4 determinam a ordem de comutação dos sinais aeb, respectivamente. As condições 5, 6 especificam a ordem do evento catch B1 e do evento catch A2.
Observação 2. O evento X pode ser o evento A1. Nesse caso, as condições 1 e 2 degeneram.
Observação 3. O evento Y pode ser o evento B1. Nesse caso, as condições 3, 4 e 5 degeneram.
Observação 4. O evento X pode ser o evento A1 e também o evento B1 pode ser o evento Y. Nesse caso, as condições 1, 2, 3, 4 e 5 degeneram.
Agora começamos a considerar o que é um implante. O implicante é caracterizado por eventos, como resultado do qual o implicante muda seu significado.
Definição 6. Um evento, como resultado do qual o implicante AND (OR) altera seu valor de 1 (0) para 0 (1), chamaremos o limite direito do implicante. O sinal correspondente a este evento será chamado de ativação. O implicante é ativado.
Definição 7. Um evento, como resultado do qual o implicante AND (OR) altera seu valor de 0 (1) para 1 (0), chamaremos a borda esquerda do implicante. O sinal correspondente a este evento será cancelado. O implicante se desliga.
Definição 8. Um implicante no qual dois limites à direita (ou dois à esquerda) não são paralelos um ao outro será chamado descontínuo.
Por enquanto, não consideraremos implantes interrompidos. Voltaremos à consideração deles abaixo.
Então temos: todas as bordas direitas dos implicantes são paralelas em pares, também as bordas esquerdas dos implicantes são paralelas em pares.
Uma propriedade importante. O implicante é ativado quando pelo menos um evento ocorre, que é a borda direita do implicante. O implicante é desativado apenas quando todos os eventos que são os limites esquerdos do implicante ocorrem.
Agora resta identificar as propriedades dos sinais que formam o implante.
Definição 9. O sinal incluído no implante será chamado de variável.
A primeira propriedade das variáveis. Ligar e desligar os sinais são variáveis.
A segunda propriedade das variáveis. Para qualquer variável de comutação (uma das quais é a borda esquerda do L implicante, a outra é algum evento X), deve haver um evento - alguma borda direita R do mesmo implicante é tal que X e R são o mesmo evento ou R > X> L.
A terceira propriedade das variáveis. Para qualquer variável inclusiva (uma de cujas opções é a borda direita do R implicante, a outra é algum evento X), deve haver um evento - alguma borda esquerda L do mesmo implicante é tal que X e L são o mesmo evento ou R > X> L.
A quarta propriedade das variáveis. Para qualquer variável (comutação X1 e X2) que não está ativada ou desativada, deve haver dois eventos: alguma borda esquerda do L implicante e alguma borda direita do R implicante, de modo que R> X1> L e R> X2> L . Caso contrário, o implicante não poderia manter um valor constante na posição desligada.
A quinta propriedade das variáveis. Para qualquer par: alguma variável de comutação e outra variável de comutação, deve haver uma sequência de variáveis que se selecionem em relação a alguns limites direitos do implicante (para diferentes captadores, as bordas à direita podem variar), começando com essa variável de comutação e terminando com essa variável de comutação . Caso contrário, o implicante não poderia manter um valor constante na posição ligado.
Sexta propriedade de variáveis. Para qualquer variável inclusiva a, se o limite direito do implicante é o evento a + (a-), essa variável é incluída no registro do implicante AND (OR) com inversão e no registro do implicante OR (AND) sem inversão. Para qualquer variável de comutação a, se a borda esquerda do implicante for o evento a- (a +), essa variável a será incluída no registro do implicante AND (OR) com inversão e no registro do implicante OR (AND) sem inversão.
A sétima propriedade das variáveis. Em virtude da quarta propriedade das variáveis, para cada variável a que não está ativando ou desativando, existe um limite direito para os implicantes R e uma borda esquerda para os implicantes L, de modo que R> a +> L e R> a-> L. Se R> a +> a-, essa variável entra no implicante de E com inversão e no implicante de OR sem inversão. Se R> a-> a +, essa variável entra no AND implicante sem inversão e no OR implicante com inversão.
As sete propriedades listadas das variáveis são propriedades necessárias do implicante. Além disso, essas propriedades são suficientes para descrever os implantes.
Observação. A descrição acima do implante não proíbe a situação em que alguma borda esquerda do implante pode ser paralela a alguma borda direita do mesmo implicante. O significado desse fenômeno é que, dependendo da velocidade dos processos paralelos, um implante em tempo real pode não ser necessário para a implementação do sinal correspondente e em tempo real ele pode não se desligar (se o limite direito funcionar mais cedo do que o limite esquerdo).
Agora vamos considerar como a forma normal de uma função lógica é construída a partir do implicante.
Definição 10. Se para algum estado o implicante estiver na posição desligado (o valor do implante AND (OR) é 1 (0)), dizemos que o implicante cobre esse estado.
Considere um certo sinal x, para o qual precisamos calcular uma função lógica. Para construir um DNF (CNF), é necessário que os implantes AND (OR) abranjam todos os estados nos quais a função x é 1 (0). Nesse caso, é necessário que nenhum desses implicantes de AND (OR) cubra estados nos quais a função x é 0 (1). Além disso, ao calcular funções lógicas, é necessário levar em consideração as especificidades dos circuitos: os implicantes devem “se sobrepor”. Ou seja, se em algum estado o implicante puder ser ativado (ou seja, um evento puder ser acionado que seja o limite correto desse implicante) e o valor da função de sinal x não mudar durante essa alternância, deverá haver outro implicante que cubra esse estado e não liga quando esse evento é acionado.
Agora precisamos esclarecer três perguntas. O que é um estado em termos de gráfico? Como determinar os estados nos quais a função de sinal x é 1 (0)? Como determinar as condições que o implante cobre?
Vamos começar com os estados. Qualquer rotulagem possível é uma condição. Como não há conflitos no CSC, cada etiqueta alcançável corresponde a um estado único (alcançável). Em estados inatingíveis, o valor da função é arbitrário e não há necessidade de considerá-los. Assim, cada estado que consideramos é descrito exclusivamente pela rotulagem correspondente. A posição de cada marcador é determinada exclusivamente pelo arco que ele marca. Cada arco é associado exclusivamente a um par de eventos (ordenados): o evento do qual o arco sai e o evento no qual o arco entra. Assim, qualquer estado atingível é descrito exclusivamente por um conjunto que consiste em pares de eventos ordenados.
Definição 11. Um par de eventos que denotam um arco marcado será gravado {P, S}, onde P é o evento de causa e S é o evento de conseqüência.
Definição 12. MM será chamado de conjunto de pares ordenados {P, S}, que descreve algum estado atingível.
Agora vamos determinar para quais estados o valor da função x é 1 e para o qual é 0. Deixe os eventos x + serem causados por n eventos A1, A2, ..., An e os eventos x causados por m eventos B1, B2, ..., Bm.
O valor da função x é 1 se:
ou 1) para cada i de 1 a n, o par {Ai, x +} pertence ao conjunto MM;
ou 2) um par {x +, S} tal que x +> S> x- pertence ao conjunto MM;
ou 3) um par {P, S} tal que x +> P> x-> x> S> x- pertence ao conjunto MM;
ou 4) um par {P, x-} tal que x +> P> x- pertence ao conjunto MM e existe i de 1 a m de modo que o par {Bi, x-} não pertença ao conjunto MM.
O valor da função x é 0 se:
ou 1) para cada i de 1 a m, o par {Bi, x-} pertence ao conjunto MM;
ou 2) um par {x-, S} tal que x-> S> x + pertence ao conjunto MM;
ou 3) um par {P, S} tal que x-> P> x + e x-> S> x + pertençam ao conjunto MM;
ou 4) um par {P, x +} tal que x-> P> x + pertence ao conjunto MM e existe i de 1 a n de modo que o par {Ai, x +} não pertença ao conjunto MM.
Agora descobrimos quais condições o implante cobre. Seja o implicante n limites esquerdo L1, L2, ..., Ln e m limites direito R1, R2, ..., Rm.
O implicante não cobre o estado descrito pelo conjunto MM se pelo menos um dos pares {P, S} pertencentes ao conjunto MM satisfizer a seguinte condição: existem i de 1 a ne j de 1 a m de modo que
1) Li e S são o mesmo evento e Rj> P> Li,
ou 2) Rj e P são o mesmo evento e Rj> S> Li,
ou 3) Rj> P> Li e Rj> S> Li.
Esta afirmação é verdadeira em virtude da quinta propriedade das variáveis.
O implicante cobre o estado descrito pelo conjunto MM se, para nenhum dos pares {P, S} pertencentes ao conjunto MM, a seguinte condição for satisfeita: existem i de 1 a ne j de 1 a m de modo que
1) Li e S são o mesmo evento e Rj> P> Li,
ou 2) Rj e P são o mesmo evento e Rj> S> Li,
ou 3) Rj> P> Li e Rj> S> Li.
Essa afirmação é verdadeira em virtude da segunda, terceira e quarta propriedades das variáveis.
Figurativamente falando, um implicante cobre o estado se todos os marcadores estiverem entre os limites esquerdo e direito do implicante. Se pelo menos um marcador estiver localizado fora desses limites, o implante não cobre esse estado.
Agora temos uma ferramenta para calcular formas normais (ainda não está claro, no entanto, ainda há uma pergunta com implantes intermitentes). Mas estamos interessados em formas normais mínimas (levando em consideração as especificidades dos circuitos). Antes de prosseguir, voltemos à consideração de implicantes intermitentes. Considere o implicante I para o sinal DNF x (o caso com o implicante OR para CNF é semelhante). Suponha que os dois limites esquerdos dos mesmos implicantes L1 e L2 não sejam paralelos um ao outro e L1> L2> x- (o caso dos dois limites direitos é considerado da mesma forma). Então deve haver dois limites corretos dos implicantes R1 e R2, de modo que, para pares de L1 e R2 e L2 e R1, as segunda, terceira, quarta e quinta propriedades das variáveis sejam satisfeitas. Se houver um limite esquerdo L3 paralelo a L1, para o par L3 e R2 as propriedades acima também deverão ser cumpridas (da mesma forma, no caso da existência de limites correspondentes, implicantes paralelos aos limites L2, R1 e R2). Mas, como vários sinais não são usados, deve haver um implicante não descontínuo com os limites L1 e R2 (e com limites correspondentes paralelos, se algum dos implicantes interrompidos os tiver). Além disso, o implicante não descontínuo consiste em menos variáveis e cobre todos os estados cobertos pelo implicante descontínuo, nos quais a função de sinal x tem um valor de 1. Daí a conclusão: os implicantes descontínuos não são extremos e não podem ser usados para calcular funções mínimas.
Mais sobre o cálculo de funções mínimas na próxima parte.