Cidade sem engarrafamentos

Capítulo Dois
( link para o primeiro capítulo )

A arte de projetar redes rodoviárias

Problemas de transporte da cidade através dos olhos de uma pessoa da Ciência da Computação

Se me recomendassem um artigo intitulado “A arte de projetar redes de estradas”, perguntaria imediatamente quantas redes de estradas foram construídas com a participação de seu autor. Devo admitir que minha atividade profissional estava longe da construção de estradas e foi recentemente associada ao projeto de microprocessadores, onde eu, entre outras coisas, estava envolvido no consumo de recursos da troca de dados. Aconteceu que minha mesa ficou em frente à janela panorâmica, que dava uma bela vista da longa seção da Rodovia Volgograd e parte do Terceiro Anel de Transporte, com seus intermináveis ​​engarrafamentos de manhã à noite, de horizonte a horizonte. E então, um dia, de repente me dei conta: “Droga, porque as complexidades do processo de troca de dados com as quais luto em um chip devem ser exatamente semelhantes às dificuldades que o fluxo de carros encontra dentro da rede de estradas”.
Provavelmente, foi apenas uma visão externa e a aplicação de métodos não tradicionais na área estudada que me deram a chance de entender a causa dos engarrafamentos e fazer recomendações sobre como superar na prática o problema.

Então, qual é a novidade da abordagem?

Historicamente, o principal objetivo das estradas é considerado a oportunidade que elas oferecem para viajar rapidamente longas distâncias (entre Roma e as províncias). Tal julgamento é justificado quando se trata da rede de rodovias interurbanas no nível federal: as cidades que eles conectam parecem pequenos pontos raros no atlas, e a maioria dos carros que viajam entre essas cidades passa pelo seu caminho sem virar para lugar nenhum.

No entanto, é necessário virar várias páginas e abrir um mapa detalhado de alguma cidade grande, pois a imagem muda imediatamente: os endereços, onde a jornada pode ser iniciada ou concluída, já são cerca de dez mil, todos bastante densos e relativamente pequeno em tamanho. Ao mesmo tempo, centenas de milhares de carros podem estar em movimento nas ruas de uma cidade ao mesmo tempo. Além disso, o objetivo de cada um deles não é apenas encher estradas já vazias, mas mover uma pessoa ou carga de um ponto com um endereço específico " X " para um ponto com um endereço específico " Y ". Em conjunto, isso significa que o sistema de transporte urbano deve ser adaptado para resolver efetivamente o problema de múltiplos endereços paralelos . Assim, as funções do sistema de transporte urbano tornam-se ainda mais semelhantes à rede telefônica ou de computadores do que à rede rodoviária entre cidades.

Considerar a rede rodoviária como um circuito de comutação para um desenvolvedor ou engenheiro de hardware no campo das tecnologias de transferência de informações é uma maneira completamente natural de falar sobre um problema, mas entre as pessoas envolvidas na pesquisa sobre problemas de transporte, essa visão é, até onde eu sei, nova.

A teoria da troca de sinal é uma ciência de engenharia estreita e, por si só, não será suficiente para planejar uma rua, entroncamento ou prever o comportamento de um fluxo de tráfego em uma seção reta e isolada de uma rodovia. Felizmente, os problemas listados acima são bem pesquisados ​​hoje e os métodos desenvolvidos para resolvê-los já foram utilizados com sucesso. A teoria da troca, por sua vez, permite que o arquiteto se livre do risco quando todos os elementos da rede rodoviária estiverem perfeitamente executados, e a cidade ainda entra em colapso no estado de transporte. Esse risco existe porque a execução de vários endereços simultâneos consome muitos recursos.
tarefa demorada, cuja chave para uma solução eficaz não é tanto a largura das ruas e a conveniência das trocas de transporte, mas a escolha competente de qual esquema de comutação específico a rede viária proposta implementará.

A partir deste trabalho, por exemplo, você descobrirá por que o tipo “arterial” de redes de transporte, que ainda são frequentemente usadas nas cidades modernas, é “ruim” e com o crescimento da população levará necessariamente a engarrafamentos. Outro resultado interessante, que está de acordo com as observações, explica por que apenas a expansão das estradas, se antes de todos os congestionamentos ocorrerem exclusivamente nas proximidades das trocas, dificilmente melhorará a situação, mesmo que o número de carros na cidade permaneça o mesmo.

Quando escrevi este artigo, era importante para mim que fosse compreensível para o arquiteto mais comum, pudesse ser útil através de seu trabalho. Tentei introduzir o leitor em questões de mudança em uma linguagem simples, para desenvolver critérios para avaliar como uma rede viária específica lidaria com a tarefa de endereçamento paralelo, usando exemplos de modelos que mostrei como usar esse conhecimento na prática.

O artigo é destinado a um amplo círculo de leitores que estão um pouco familiarizados com o curso universitário de matemática, a teoria dos algoritmos e estão prontos para dedicar de 1 a 5 dias a ele.

Separação e fusão de fluxos de automóveis

Obviamente, para muitos motoristas, a observação é que as dificuldades de trânsito surgem principalmente nos locais onde os carros, por algum motivo, são forçados a mudar de faixa. Os exemplos incluem garfos, estreitamentos, áreas de entroncamento e estradas de acesso às rodovias, seções de uma rodovia onde algumas faixas são bloqueadas por um acidente ou reparo de estradas.
Nesta seção, será feita uma tentativa de fornecer uma descrição quantitativa dos processos que ocorrem nesses casos, e começaremos entendendo como os carros são reconstruídos de uma pista para outra.

Duas estratégias para reconstruir em uma linha adjacente

O movimento do tráfego ao longo da rodovia tem uma irregularidade natural: alguém prefere dirigir um pouco mais rápido, alguém um pouco mais devagar, entre alguns carros a distância diminui e fica pouco confortável para dirigir, enquanto entre os outros aumenta tanto que permite que os carros se encaixem lá de faixas adjacentes. O aparecimento de tais lacunas no fluxo da faixa adjacente diretamente no lado do motorista aleatório pode ser frequente ou não muito. Se, no momento em que ele precisar fazer uma manobra, não houver lacuna, o motorista poderá recorrer a pelo menos duas estratégias comportamentais:

Estratégia No. 1
Várias lacunas adequadas podem simplesmente ser localizadas próximas à sua localização. Se o movimento for denso o suficiente, é improvável que o motorista possa aumentar a velocidade e captar a folga necessária, mas diminua um pouco o movimento e deixe o fluxo vizinho se ultrapassar para igualar a lacuna que estava originalmente atrás - não haverá grandes problemas. Os custos dessa estratégia são óbvios: o próprio motorista e os carros que estão atrás na pista perdem algum tempo devido à necessidade de reduzir a velocidade.

Estratégia No. 2
Para esperar, você precisa ter paciência e ter o tempo necessário para isso. Uma alternativa pode ser uma tentativa de realizar a manobra necessária "aqui" e "agora". De acordo com essa idéia, o motorista dá um sinal para os carros atrás da faixa na qual ele vai se mover. Aqueles, por sua vez, em resposta ao seu sinal, deviam desacelerar um pouco e "soltar" para a frente, os carros se movendo na frente deles, dando à lacuna o tamanho necessário, formarão seu fluxo. Os custos de tempo, neste caso, são distribuídos entre os carros da pista onde o motorista acabou reconstruindo.

Na vida real, as duas estratégias estão envolvidas ao mesmo tempo: primeiro, o motorista diminui a velocidade, aguardando uma lacuna relativamente grande no fluxo da pista vizinha e só então dá um sinal aos carros que se deslocam nela sobre sua intenção de realizar uma manobra de reconstrução.

Obviamente, entradas, rampas e passagens estreitas não são a única razão para a faixa de faixa mudar, o que vale a pena lembrar ao projetar estradas. A capacidade dos carros com velocidades mais altas de ultrapassar o tráfego sem pressa é necessária para que a situação na rodovia não se degrade a uma grande fila que se arrasta à velocidade do trator mais lento. No entanto, o problema da coexistência de veículos em movimento em diferentes velocidades na estrada tem uma natureza um pouco diferente e pode ser separado das questões consideradas neste artigo, uma vez que o processo de ultrapassagem e os rearranjos associados não são para as ações forçadas do motorista que exigem que ele se apresse . Se houver tempo de espera, então, de acordo com a teoria das probabilidades, é uma oportunidade conveniente para executar uma manobra que o motorista deve deixar sozinho e, para isso, não interfere necessariamente no movimento de outros motoristas.

Custo de um movimento
O comportamento dos motoristas na realidade pode ser muito difícil, mas é importante para nós, antes de tudo, que o resultado obtido nas condições do modelo permaneça plausível: cada movimento forçado de um carro de uma faixa para outra impõe uma penalidade temporária aos participantes do trânsito.

Vamos agora avaliar como a quantidade de tempo perdido depende da densidade de carros na estrada.

Vamos considerar o movimento ao longo de cada pista como um fluxo separado. Tentando permanecer a uma distância confortável de carros que estão na mesma faixa, os motoristas reservam, assim, uma parte de um determinado comprimento característico d no fluxo. Deixe os carros caírem em um fluxo por unidade de comprimento. Concordamos em chamar a densidade de fluxo pequena ou, da mesma forma, dizer que ρ é pequeno se o produto ρ × d for muito menor que a unidade.

No momento em que o motorista perceber a necessidade de passar para a próxima linha, a probabilidade de que a seção da quantidade d que ele iria ocupar não seja livre, em ρ pequeno será aproximadamente proporcional ao ρ em si. Se o evento descrito realmente ocorrer, no total, dois carros competindo por um lugar sofrerão como resultado de manobras algum atraso no valor constante médio δ .

Supondo que ρ seja pequeno, a probabilidade de que suas ações neste momento afetem o movimento de outros carros pode ser negligenciada. Assim, na primeira ordem de pequenez em relação a ρ , a perda de tempo de um movimento será α ⋅ ρ , onde o coeficiente α é uma quantidade empiricamente mensurável, dependendo da cultura, clima, limites de velocidade (e assim por diante), mas permanecendo aproximadamente constante localmente no tempo e por nesta cidade como um todo.

A intensidade das perdas no local antes da saída
Os carros que partem para o congresso, antes de chegarem à rampa (Fig. 2), precisam, às vezes até várias vezes, ser reconstruídos na fila adjacente à direita. Cada uma dessas manobras dificulta a movimentação e, como resultado, a velocidade média na seção antes da saída é visivelmente mais baixa do que nas seções "trânsito" (privadas de saídas, "entradas" e bifurcações) da rodovia.


fig. 2

Para passar uma parte do caminho em uma velocidade mais baixa - vire para os motoristas (e seus passageiros) uma quantidade adicional de tempo gasto na viagem. Em outras palavras, a área da rodovia diretamente adjacente à rampa é um gerador constante de perdas temporárias.

Suponha que a velocidade média da máquina ν e a densidade do fluxo ρ no limite frontal desta região sejam as mesmas para todas as bandas.

Suponha, além disso, que a densidade ρ e a vazão q saindo da saída (o número médio de carros subindo a rampa por unidade de tempo) sejam simultaneamente pequenas e s é o número de faixas na rodovia. Para chegar à saída, o motorista fará 1 a s de manobras de reconstrução. Se a densidade do fluxo na rampa for muito menor que ρ , somente a última manobra lhe custará praticamente "de graça", enquanto o restante causará, em qualquer caso, perdas de α ⋅ ρ . Em média, você terá que realizar (0 + 1 + 2 + ... + s - 1) / s = ( s - 1) / 2 manobras "caras".

Dadas as dificuldades causadas por todos os carros que partem para o congresso, podemos escrever a fórmula para a intensidade de perdas temporárias:

I _out = q ⋅ α ρ ⋅ ( s - 1) / 2 = ( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 - 1 / s )

O valor p = ( sρν ) nada mais é do que a vazão de todos os carros que se deslocam pela estrada na direção em questão (o número médio de carros que passam pela coluna por unidade de tempo). A última observação nos dá a oportunidade de reescrever a fórmula para I de uma forma mais simétrica:

I _out = ( α / 2 ν ) ⋅ pq ⋅ ( 1-1 / s )

Taxa de perda na seção adjacente da via de acesso
A situação que surge na estrada atrás do local onde a estrada de acesso se conecta a ela repete amplamente a situação no local em frente ao congresso, embora haja algumas diferenças.
Deixe um pequeno fluxo de carros de força q pela rampa lateral derramar no tráfego principal da rodovia (Fig. 3).


fig. 3

A rampa tem apenas um comprimento finito; portanto, todos os carros recém-chegados, quer ou não, devem ser construídos na faixa da extrema direita da rodovia. Como resultado, a densidade de tráfego na faixa mais à direita é localmente mais alta que a média na estrada, portanto alguns motoristas decidem mudar de faixa para uma linha adjacente menos movimentada à esquerda, o que, por sua vez, leva a um aumento local de densidade já na segunda tira. Esse processo de migração entre bandas continuará até que a densidade do fluxo seja nivelada em toda a largura da rodovia. Supondo que a velocidade média ν seja a mesma para todas as n bandas, podemos esperar que, após a conclusão dos processos de migração, a potência de fluxo em cada uma delas aumente exatamente (1 / s ) ⋅ q .

Para ver quanto custa esse “castling” para os motoristas, primeiro calculamos a potência de todos os fluxos de migração. O fluxo da rampa para a primeira faixa da rodovia já sabemos: é igual a q . Para obter um equilíbrio na forma de um aumento de (1 / s ) ⋅ q , o fluxo para a segunda faixa do lado da primeira já deve ser (1 - 1 / s ) ⋅ q , da segunda para a terceira - (1 - 2 / s ), q , do késimo lado ao ( k + 1) th - (1 - k / s ) ⋅ q . De acordo com a última fórmula, a capacidade do fluxo de migração para a faixa mais à esquerda será (1 - ( s - 1) / s ) ⋅ q = (1 / s ) ⋅ q , conforme ordenado pelo senso comum.

Como sabemos a penalidade de tempo de uma única reconstrução e o poder de todos os fluxos migratórios, agora podemos calcular a intensidade total das perdas geradas por eles:

I _in = α ρ ⋅ q + α ρ ⋅ (1 - 1 / s ) ⋅ q + α ρ ⋅ (1-2 / s ) ⋅ q + ... + α ρ ⋅ (1 / s ) ⋅ q =

α ρ q (1 + 2 + ... + s ) / s =

α ρ q ( s + 1) / 2 =

( α / 2 ν ) ⋅ q ⋅ ( sρν ) ⋅ (1 + 1 / s ).

Lembrando novamente que sρν é a potência p do fluxo de todos os carros ao longo da estrada, obtemos a fórmula de custo em sua forma final:

I _em = ( α / 2 ν ) ⋅ pq ⋅ (1 + 1 / s ).

Taxa de perda simétrica do garfo
Nos parágrafos anteriores, encontramos perdas com a interação dos fluxos, um dos quais era necessariamente grande e o outro era necessariamente pequeno. Para demonstrar a abordagem para resolver problemas quando as capacidades de ambos os fluxos são comparáveis ​​em magnitude, vamos considerar outro extremo: um garfo no qual as duas direções da "filha" são igualmente populares para os motoristas (Fig. 4).


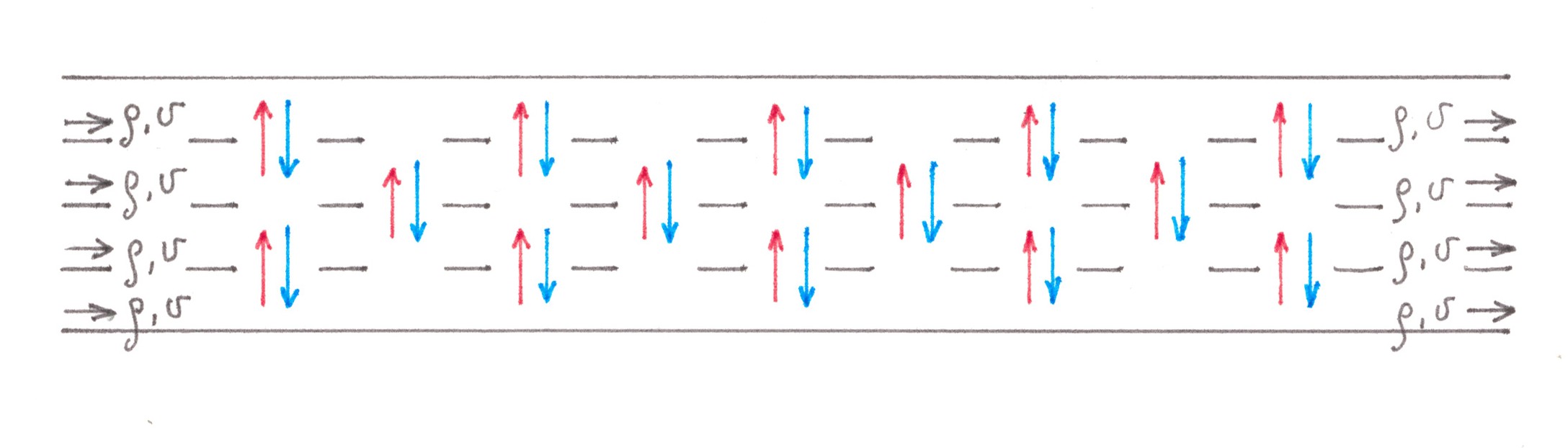
fig. 4

Por conveniência, os carros que vão para a direita na bifurcação serão chamados de "azul" e os carros que sairão para a esquerda - "vermelho". Inicialmente, carros de ambas as "cores" se movem misturadas, dispersas entre as duas faixas da rodovia. À medida que se aproximam do cruzamento, os carros vermelhos começam a vagar lentamente na direção das n faixas da esquerda e os azuis na direita, nas faixas da direita: a migração flui nas duas direções entre as faixas adjacentes. Ao contrário do exemplo da via de acesso, esses fluxos não são mais "relativamente pequenos". A propósito, apenas entre as duas faixas centrais há uma troca de tráfego forçado, cuja intensidade em qualquer uma das direções (da esquerda para a direita ou da direita para a esquerda) é igual a um quarto da potência de todo o fluxo que se move ao longo da rodovia de carros. Felizmente, nessa situação, existe uma maneira boa o suficiente para estimar os custos gerados. Primeiro, observamos que o processo de dividir os carros em “vermelho” e “azul” provavelmente começa muito antes da bifurcação e prossegue lentamente; portanto, por um lado, deve ter pouco efeito na densidade do tráfego em uma linha separada e, por outro, fazer a migração os fluxos se estendem por longas distâncias, dando a oportunidade de representar cada um deles como uma combinação de um grande número de fluxos de baixa potência (Fig. 5).


fig. 5

Como agora estamos falando de pequenos fluxos, embora em números maiores, nada nos impede de reduzir o problema em consideração para os já resolvidos. Divida mentalmente a estrada no centro em duas partes iguais e conecte-as a um grande número de estradas de ponte de pista única, permitindo que carros vermelhos cheguem ao lado esquerdo e carros azuis à direita (Fig. 6). Devido à simetria óbvia, ao calcular as perdas geradas, podemos nos concentrar em máquinas de qualquer cor, por exemplo, azul, e no final apenas o dobro do resultado.


fig. 6

Portanto, deixe velocidade ν e densidade ρ sejam as mesmas para todas as faixas e permaneça constante em toda a área em que os carros são separados por cores.Nesse caso, a vazão de todos os carros que circulam pela estrada será:

p = 2 sρv .

Seja q ₁ , q ₂ , ... q _m denota o fluxo de carros azuis que se deslocam ao longo de jumpers imaginários para a metade direita da rodovia. Suponha que, pouco antes da seção de separação em cada rodovia, as duas cores sejam representadas com proporções iguais de 50%, o que implica que no total
q ₁ + q ₂ + ... + q _m sejam iguais a sρv / 2, que é p / 4.

Perdas geradas pelo fluxo q_i , devido à sua pequenez, podemos calcular pela fórmula:

I _i =I _out +I _in = (α/ 2ν)⋅(p/ 2)⋅ q _i (1-1/s) + (α/ 2ν)⋅(p/ 2)⋅ q _i (1 + 1 /s) = (α/2ν)p q _i

Somando a última expressão sobre todos osi, Localizar a perda gerada carros só azul:

I _azul = ( α / 2 ν ) ⋅ p ⋅ ( q ₁ + q ₂ + ... + q _m ) = ( α / 2 ν ) p ² /4.

perda completa, como já foi mencionado, irá ser dobrada e a quantidade duas vezes como:

I _div = ( α / 2 ν ) p ² /2.

Análise das fórmulas obtidas
Se separarmos a intensidade Iisto é, a quantidade de tempo que o total de participantes perdidos por segundo pela quantidade de fluxo lateral q , que por definição é igual ao número de carros que conectam ou saem da rodovia em um segundo, obtemos as perdas médias geradas por um desses carros:

i _in = I _in / q = ( α / 2 ν ) ⋅ p ⋅ (1 + 1 / s )

i _out = I _out / q = ( α / 2 ν ) ⋅ p ⋅ (1 - 1 /s )

Talvez o mais importante nessas fórmulas seja a proporcionalidade direta entre o fluxo de potência dos carros na rodovia pe os custos unitários i . Tudo parece que um carro está tentando entrar, ou vice-versa - para deixar o fluxo do movimento principal, causando danos constantes a todos os motoristas próximos.

A segunda observação interessante e muito inesperada diz respeito ao efeito extremamente fraco sobre a intensidade das perdas geradas do número de faixas próximas à rodovia diretamente ao lado do entroncamento. Como você pode ver, olhando para a fórmula de I _out , o congresso é geralmente o mais barato para uma estrada de pista única ( s = 1, i _out = 0), e as dificuldades causadas pela estrada de acesso adjacente para uma via de três e seis vias diferem em apenas

100% ⋅ [(1 + 1/3) - (1 + 1/6)] / (1 + 1/3) = 12,5%.

Se levarmos em conta que todo carro que já entrou no trânsito na rodovia acabará por abandoná-lo, parece bastante legalusar o valor unificado i _av = ( i _in + i _{in em} vez de i _in e i _out ) / 2 = ( α / 2 ν ) ⋅ p .



Apesar da falta na fórmula para i _av uma dependência explícita sobre o número de bandas, devemos lembrar que a sua saída (ver sugestões para I de _em e eu de _fora ) é essencialmente baseada no pressuposto de uma densidade pequena máquina na estrada, por isso é improvável que dão resultados satisfatórios, sendo aplicada a uma estrada muito estreita com muito tráfego.

Conclusões preliminares
Em áreas próximas a cruzamentos, o tráfego ocorre inevitavelmente, afastando os motoristas, reduzindo a velocidade média, o que leva a um aumento na densidade de carros e, consequentemente, à possível ocorrência de engarrafamentos. Os custos de tempo associados à separação e fusão dos fluxos de automóveis serão chamados de comutação.

Perdas de um tipo semelhante estão presentes de uma maneira ou de outra em qualquer esquema de comutação: seja uma rede telefônica ou de computador, um microprocessador multinúcleo ou um serviço de entrega de correio.

Quando um motorista entra ou, inversamente, deixa o tráfego na rodovia, os custos de troca incorridos por suas ações são proporcionais à potência do fluxo de carros observado naquele momento na rodovia.

Para reduzir as perdas de comutação em toda a cidade, é necessário considerar cuidadosamente a rede de estradas implementada na fase de projeto. Um pouco mais tarde, analisaremos essa tarefa em detalhes, mas algumas recomendações óbvias podem ser listadas agora:

1. as perdas de comutação são proporcionais à capacidade de fluxo na rodovia - não é necessário ampliar as estradas sem a necessidade, duas pequenas rodovias são duas vezes melhores que uma grande;
2. as perdas de comutação são proporcionais à potência dos fluxos laterais - vale a pena projetar a rede para que o motorista tenha que se afastar o mínimo de vezes possível durante sua jornada;
3. a interferência mútua causada pelos motoristas dos fluxos principal e lateral deve diminuir em escala em toda a cidade se você tentar evitar rotas que se sobreponham apenas em uma seção curta da pista em um fluxo.

Pré-requisitos econômicos para a existência de cidades.
Modelo de cidade de acesso uniforme

Talvez a primeira coisa a iniciar qualquer projeto de planejamento (ou re-planejamento) do sistema de transporte da cidade seja tentar determinar que tipo de migração a cidade realmente precisa agora e como suas necessidades mudarão no futuro.

Essa análise pode ser realizada se você primeiro dividir a cidade em zonas territoriais não muito grandes, mas não muito pequenas, e depois para cada par dessas zonas indicar qual número aproximado de viagens para um lado ou outro é necessário por seus habitantes uma ou outra vez. do dia. Ao colocar as previsões feitas em uma mesa quadrada, você receberá uma matriz das necessidades de migração dos moradores da cidade.

É para essa matriz que vale a pena procurar uma rede que permita que motoristas e passageiros passem o mínimo de tempo possível em uma viagem separada e exigindo das autoridades da cidade o mínimo de recursos possível para sua construção.

Quando se trata de cidades existentes, aqui é importante não cometer um erro e não substituir o número de viagens que as pessoas realmente precisam pelo número de viagens que historicamente foram estabelecidas sob a influência de alguns obstáculos ou dificuldades no momento do trabalho de design. Provavelmente, a rede de transporte de Berlim "antes" e "depois" da queda do muro de separação pode servir como a ilustração mais impressionante do que foi dito.

Esta seção tratará principalmente de questões humanitárias nas quais eu não sou especialista, mas acho que discuti-las como amador é, no entanto, mais correto do que simplesmente evitar o problema.

Para melhor representar as necessidades migratórias da população, vale a pena começar com a pergunta fundamental: "Por que as cidades realmente precisam e que função útil elas desempenham?" .

Vamos tentar responder não como moradores comuns de cidades (e vilarejos), mas da perspectiva da pessoa responsável pelo processo de urbanização em algum estado grande e desenvolvido. Deste ponto de vista, não é mais importante quais motivos históricos fizeram tantas pessoas amontoadas em um pequeno pedaço de terra, ou as razões pelas quais continuam a fazê-lo agora, é importante - que efeito econômico cria cidades de um tamanho ou outro e para devido a quais mecanismos esse efeito é alcançado.

Na minha opinião, a principal razão para a existência de grandes cidades é, por um lado, a oportunidade para as empresas de tecnologia encontrarem funcionários de profissões raras e, por outro lado, a oportunidade para as pessoas que dominam profissões raras venderem seus serviços para empresas interessadas em termos competitivos. Em uma cidade pequena (não especializada), a produção de muitos bens e serviços é simplesmente impossível ou coloca as empresas de tecnologia e seus funcionários que a implementam na posição de reféns mútuos, sem dar alternativas a uma ou a outra.

Por exemplo, considere a profissão não tão rara de um professor de literatura da escola. Segundo as estatísticas, a necessidade deles é: aproximadamente 1 professor por 1000 habitantes. Em uma escola regular, 3-4 pessoas ensinam literatura. A escolha de um emprego para professor de literatura pode ser considerada competitiva se houver pelo menos 4-5 escolas secundárias em sua cidade, que, em termos de população, é de cerca de 15 mil pessoas.

Aparentemente, pessoas com especialidade em engenharia se sentem à vontade no mercado de trabalho em cidades com uma população de pelo menos 100 mil. É claro que existem também essas profissões, cuja demanda aparece apenas em cidades com um milhão de pessoas, mas o senso econômico de milhões de cidades permanece um mistério para mim.

Depois de tudo o que foi exposto, duas hipóteses parecem bastante motivadas (cuja validade, no entanto, não afeta a verdade do conteúdo principal do artigo):

1. as viagens mais freqüentes que o adulto médio precisa percorrer distâncias que capturam 4-5 dos trabalhos mais promissores para ele;
2. para uma parte significativa da população que possui as profissões raras e economicamente mais valiosas, a distância das viagens mais frequentes pode ser comparável ao raio da cidade.

Como uma reflexão aprimorada das hipóteses 1) e 2), em meus exemplos usarei frequentemente o modelo de uma cidade com “acesso uniforme”, que pressupõe que o poder dos fluxos de viagens populares seja o mesmo entre dois quartos dela ou, em outras palavras, em todas as células da matriz as necessidades de migração valem o mesmo número positivo. Se você olhar aleatoriamente para os registros de viagens feitas em uma cidade durante o dia, para a próxima viagem marcada, todos os trimestres terão as mesmas chances de ser o início dessa viagem e servi-la como final, e não há relação entre a posição de "inicial" e "final" »Quartos não devem ser observados.

Redes simples de topologia de rede

Vamos tentar aplicar as idéias descritas nos parágrafos anteriores a alguns tipos de planos urbanos retirados da vida.

Cidade linear
Os primeiros grandes assentamentos originaram-se predominantemente ao longo da costa, em áreas de uma faixa fina de terra entre o mar e as falésias, ou ao longo dos caminhos de estradas movimentadas; assim, no processo de crescimento, eles adquiriram estreitas fronteiras alongadas. Muitos desses assentamentos sobreviveram até hoje, mantendo sua forma alongada e se transformando em cidades modernas (ilustração abaixo).


(área isolada do Rio de Janeiro, autor desconhecido)

Muitas vezes, em uma cidade assim, existe apenas uma estrada larga em torno da qual ela é construída. Suponha que cada trimestre (zona de divisão territorial) gere um fluxo de viagens de uma única capacidade, de todos esses bairros - n , e a própria cidade obedeça ao modelo de migração de “acesso uniforme”.


fig. 7

Vamos tentar encontrar, para as condições listadas acima, como o tempo médio de viagem e a área necessária da estrada mudam com o aumento de n .

Portanto, deixe todos os quartos terem a mesma forma e tamanho, e seu número aumenta em λ (lambda) vezes. Obviamente,

• o comprimento da estrada principal aumenta em um fator de λ .

Em virtude do modelo adotado de “acesso uniforme”, 50% das viagens iniciadas na metade direita da cidade terminam na metade esquerda (exatamente o oposto), portanto, com um aumento no número de quartos por um fator de λ, a potência do fluxo que passa pelo meio da cidade também aumentará em λ vezes Um raciocínio semelhante com a mesma conclusão será verdadeiro se, em vez do meio, considerarmos qualquer ponto da cidade em uma determinada proporção (1: 3, 2: 5), o que implica que

• o fluxo de potência dos carros na estrada principal aumenta em um fator de λ .
• o número de faixas da estrada principal requeridas em cada trecho aumenta em um fator de λ .

Mais ou menos óbvio que a duração média da viagem e com ela

• o tempo líquido de viagem gasto na cobertura da distância aumenta em um fator de λ .

Tudo o que resta para nós é calcular quantas vezes o tempo perdido devido aos custos de troca em uma viagem aumentará. Em cada trimestre, um fluxo lateral de unidade de energia entra e sai, que juntos geram perdas temporárias de intensidade:

I = I _in + I _out = ( α / 2 ν ) p ⋅ 2,

onde p é a vazão na estrada principal. Já sabemos que o número de quartos e a vazão na estrada principal aumentam à medida que λ ; portanto, o tempo total de perdas geradas pela rede aumenta em um fator de ² . Por outro lado, o número de viagens geradas pela rede, entre as quais, como resultado, todas essas perdas são distribuídas, aumenta em um fator de λ , de onde obtemos isso.

• o tempo líquido de viagem perdido devido aos custos de troca aumenta em um fator de λ .

Vamos coletar todos os resultados em um prato:

Topologia linear
O número de pontos de endereço (quartos) da capacidade da unidade ........................... n
A área total das estradas ............................................... ........................................ O ( n ² )
Tempo de viagem puro
gasto em cobrir a distância .............................................. ..... O ( n )
Tempo de viagem puro
perdido devido a custos de troca ............................................ ......... O ( n )
O número de nós de comutação ............................................... .................................... O ( n )
O número de nós de comutação, levando em consideração a potência dos fluxos laterais ..................... O ( n )

A notação usada: " y = O ( x )" significa que as quantidades x e y são funcionalmente dependentes e, quando x cresce sem limites, a razão x / y tende a um número finito diferente de zero.

Cidade celular
O segundo método de planejamento bastante comum é organizar os blocos na forma de uma matriz retangular, semelhante à maneira como as porções são colocadas em uma barra de chocolate.

Concordamos em chamar essas cidades de "Celular".


(Los Angeles, foto: Stepanov Glory)

A Figura 8 mostra um diagrama da Cidade Celular, composta por n (considerando as "metades") dos bairros, formando um quadrado regular. Os quartos são separados um do outro por um total de √ n estradas, correndo condicionalmente de oeste para leste, e outras √ n estradas, estendendo-se do sul para o norte. No total, essas estradas formam cruzamentos √ n × √ n , cada um dos quais pode ser feito como um cruzamento de semáforo ou implementado através de uma ponte e viadutos.


fig. 8

Independentemente de o tráfego nas ruas ser unidirecional ou bidirecional, qualquer viagem do ponto "A" ao ponto "B" em uma cidade quadriculada pode ser realizada ao longo de uma rota que passa por não mais que duas ruas e não requer mais que uma curva no cruzamento. querido

Suponha que, como no exemplo anterior, cada trimestre gere um fluxo de viagens de capacidade unitária, e as necessidades de migração da população sejam descritas pelo modelo de “acesso uniforme”. Vamos calcular, agora para a cidade celular, as leis pelas quais o tempo médio de viagem e o consumo de recursos da construção de uma rede viária aumentam o número de trimestres.

Se o número de quartos aumentar por um fator de λ , então:

• a área da cidade aumenta em λ vezes e suas dimensões lineares, mantendo as proporções -
  em √ λ ,
• a duração média do percurso e o tempo líquido para percorrer a distância, sendo proporcional às dimensões lineares, aumentam √ λ vezes,
• o número de ruas e o número de bairros adjacentes a uma rua aumentam √ λ vezes,
• a potência do fluxo de tráfego, sendo proporcional ao número de trimestres com os quais o fluxo está "em contato" (uma explicação desse fato será dada posteriormente), aumenta em √ λ vezes,
• a área requerida de todas as estradas cresce à medida que (número de ruas) × (comprimento de uma rua) × (potência do fluxo da rua) = √ λ ⋅ √ λ ⋅ √ λ = λ √ λ

Os fluxos laterais são divididos naqueles que vão de ou para os bairros e os fluxos de tráfego que passam de uma rua para outra em seus cruzamentos. O primeiro, de acordo com as condições, sempre permanece igual à unidade; depois do segundo, se levarmos em conta que há muito mais bairros na cidade do que bairros em uma única rua, quase todo o tráfego que se move por ela chega ou sai da rodovia. Como resultado, a mudança na magnitude dos fluxos laterais do segundo pode ser estimada pela fórmula (mudança na potência do fluxo da rua) / (aumento no número de cruzamentos em uma rua específica) = √ λ / √ λ = 1. A igualdade da última razão com a constante sugere que esses fluxos não mudam especialmente um aumento no número de quartos, portanto, o aumento nos custos de comutação gerados pela rede como um todo será: (aumento no número total de quartos + cruzamentos) × (alteração no valor do fluxo em uma única rua) = λ √ λ . Como o poder do fluxo de viagens gerado por todos os trimestres aumentou em λ , então

• o tempo líquido de viagem perdido devido aos custos de troca aumenta em √ λ

Imagine o resultado na forma de um tablet:

"Topologia celular"
O número de pontos de endereço (quartos) da capacidade da unidade ........................... n
A área total das estradas ............................................... .................................... O ( n √ n )
Tempo de viagem puro
gasto em cobrir a distância .............................................. ... O (√ n )
Tempo de viagem puro
perdido devido a custos de troca ............................................ ....... O (√ n )
O número de nós de comutação ............................................... .................................... O ( n )
O número de nós de comutação, levando em consideração a potência dos fluxos laterais ..................... O ( n )

Comparando as redes linear e celular, é difícil não notar que o aumento dos recursos necessários para a construção e o tempo gasto em uma viagem com o crescimento da cidade para a primeira rede são muito mais rápidos do que para a segunda. Por exemplo, uma cidade celular de 100 quartos requer 10 vezes menos asfalto, e uma viagem por ela requer uma média de 10 vezes menos tempo do que o necessário em uma cidade linear do mesmo tamanho. Portanto, faz sentido usar redes de estradas com topologia linear apenas em cidades muito pequenas.

Se, por algum tempo, você esquecer a existência de custos de mudança, a topologia celular pode ser considerada uma maneira ideal de projetar redes de estradas, pois fornece uma estimativa O assintoticamente ideal para a duração média da viagem e a área de estrada necessária. De fato, para qualquer localização mais ou menos “compacta” da cidade (com acesso uniforme), a duração da viagem não será mais lenta que a raiz quadrada de sua área, que geralmente é diretamente proporcional à população. Como resultado, obtemos o mesmo O (√ n ).

O fato de uma rota típica na cidade celular ser uma “esquina” e não uma linha reta, em princípio, dá o direito de procurar maneiras melhores de planejar cidades, mas é improvável uma economia de 20% (que é o quanto você pode ganhar no limite se os carros aprenderem a atravessar paredes) é improvável um dia eles forçarão os arquitetos a abandonar o arranjo retangular de ruas e estradas.

O limite mais baixo possível do custo de construção (e manutenção) da rede pode ser obtido lembrando que cada carro reserva parte da faixa para o seu movimento, como resultado, a área total de estradas é proporcional ao produto do tempo médio de viagem (duração média da viagem) pelo número de carros na cidade : O (√ n ) × O ( n ) = O ( n √ n ) (compare com a tabela da cidade celular).

Se falamos sobre a quantidade de tempo perdido em viagens devido a custos de mudança, surpreendentemente, sua relação com a quantidade de tempo necessária para cobrir a distância não depende assintoticamente do número de quartos individuais na cidade celular ou linear (O (√ n ) / O (√ n ) = O (1), O ( n ) / O ( n ) = O (1)). Em outras palavras, a porcentagem de tempo perdido em viagens devido à troca de eventos na cidade grande e na pequena será a mesma. A partir disso, podemos concluir que, se não houvesse problemas sérios com os custos de troca em uma cidade pequena (digamos, eles chegassem a 10-20%), então em uma cidade grande eles ainda não deveriam ser observados, e se fossem, sozinhos eles eles não vão a lugar algum, não importa como a cidade tenha crescido e ampliado.

Como não sabemos qual das alternativas é verdadeira (ou melhor, sabemos que existem problemas com o tráfego de automóveis nas grandes cidades), vale a pena tentar melhorar a topologia da Cidade Celular, para que os custos de troca nela diminuam pelo menos por um tempo constante.

Exemplos úteis de redes irrealistas

Vamos ver se a topologia celular segue as recomendações que desenvolvemos analisando a alternância de fluxos na estrada.

1) Não amplie estradas sem a necessidade.
Sim. O tráfego é distribuído por muitas estradas (compare com a Cidade Linear).

2) Evite criar condições quando precisar fazer um grande número de voltas em uma viagem.
Sim. Qualquer viagem provavelmente será realizada ao longo de uma rota que exige apenas uma curva nas ruas da cidade.

3) Evite situações ao viajar em um trecho da estrada, cujas rotas possuem apenas um trecho pequeno do caminho comum.
- Aqui, talvez, haja algo para trabalhar. Apesar do número mínimo de voltas por viagem, sua rota como parte do fluxo da rodovia principal passa por um grande número de nós de comutação (O ( n )), em cada um dos quais é desperdiçado um tempo valioso.

A última observação motiva a investigar a seguinte pergunta: “Qual é o valor mínimo do número médio de nós de comutação através dos quais uma jornada deve passar dentro de uma rede de estradas conectando n blocos?”

A tarefa de procurar por uma rede desse tipo faz sentido, é claro, apenas com a condição de que o número de fluxos combinados ou compartilhados por qualquer nó de comutação seja preliminarmente limitado de cima por um determinado valor fixo. Caso contrário, você sempre poderá apresentar uma rede viária com n pontos de endereço e um único mega-entroncamento.


(autor desconhecido)

É muito mais fácil investigar o problema real se anteriormente era possível revelar pelo menos parte dos padrões usando alguns exemplos simples, mesmo que nem todos realistas. Seguindo essa lógica, esqueceremos temporariamente as limitações geométricas de construir uma estrada para os viajantes percorrer distâncias, concentrando toda a atenção em como as redes abstratas resolvem o problema do endereçamento paralelo. Em relação aos nós de comutação, assumiremos por enquanto que cada um deles divide o fluxo em duas partes (o nó de divisão) ou combina dois fluxos em um.


fig. 9

Árvore de endereços
Deve haver um ponto de endereço inicial onde todas as viagens começam sem exceção, e outro n ponto de endereço final nos quais eles terminam com igual probabilidade (Fig. 9).

É necessário construir uma rede de transporte que permita que a viagem passe pelo menor número possível de nós de comutação.

A solução óbvia (para programadores), que se propõe aqui, é usar uma árvore binária balanceada, ao mesmo tempo em que você precisa colocar um único ponto de partida no topo da árvore e colocar os n pontos de acabamento restantes um em cada uma das suas folhas (Fig. 10). A rede construída da maneira descrita será chamada de árvore de endereços direta.


fig. 10

Mudando as direções de todos os fluxos para o oposto na árvore de endereços direta, obtemos assim a árvore de endereços reversa, cujo objetivo é conectar n pontos de partida com um único acabamento.

Nos casos em que n é uma potência de dois, qualquer rota dentro da árvore Address passa exatamente pelo log ₂ n nós de comutação, que é indubitavelmente (assintoticamente) menor que o mesmo indicador para uma rede com Cellular (O (√ n )) ou Linear ( O ( n )) topologia.

Os dois tipos mais simples de redes logarítmicas
Usando redes "em forma de árvore" como blocos de construção, não é difícil generalizar a solução anterior para o caso quando há mais de um ponto de partida, mas -k . Existem duas maneiras fáceis de fazer isso.

A primeira maneira é usar a árvore de endereços reversa para coletar primeiro as rotas de todas as viagens em um fluxo comum e, em seguida, usando a árvore de endereços direta, divida esse fluxo em subfluxos, cada um endereçado ao seu destino (rede na parte superior na Fig. 11 )


fig. 11

Se k e n são potências de dois, no final, qualquer rota passa exatamente pelos nós de comutação log ₂ k + log ₂ n . Redes construídas de acordo com o algoritmo descrito acima, concordamos em chamar Logarítmica (unidirecional) com mesclagem preliminar .

A segunda maneira de resolver o mesmo problema pode ser obtida revertendo na primeira solução a ordem das operações de fusão e separação. Sua implementação é a seguinte: para cada ponto de partida, crie um conjunto exclusivo de duplicatas imaginárias de todos os pontos de endereço final e conecte-o a essas duplicatas (nem um pouco imaginárias) com uma árvore de endereços direta.

Para concluir a construção da rede, resta apenas conectar agora cada ponto de chegada a uma árvore de endereços reversa com k duplicatas imaginárias (a rede da parte inferior na Fig. 11).

Sempre que n e k são potências de dois, o número de nós de comutação no caminho de qualquer rota dentro da rede recém-construída será novamente igual ao log ₂ k + log ₂ n . Concordamos em chamar redes deste tipo (unidirecionais) de logarítmicas com separação preliminar .

Transformação de redes unidirecionais em simétricas
Em geral, redes unidirecionaisligaremos para qualquer rede se os pontos de endereço conectados por ela forem estritamente divididos em início e término. Por padrão, para redes unidirecionais, será assumido que ele fornece pelo menos uma rota de movimento possível de qualquer ponto inicial para qualquer ponto final.

Além de uma jornada ao longo da vida, é difícil citar exemplos em que quando alguns pontos de endereço serviriam como rotas apenas no começo e outros - só poderiam ser o seu fim. Aproximaremos nosso raciocínio da realidade se incluirmos redes nas quais dois pontos de endereço estão conectados por rotas em ambas as direções. Concordamos em chamar essas redes de simétricas .

De fato, não existe um hiato ideológico entre redes unidirecionais e simétricas: cada rede simétrica também pode ser usada como uma rede unidirecional, e cada rede unidirecional, conectando inicialmente um número igual de pontos de partida e chegada, pode ser transformada em uma simétrica (Fig. 12).


fig. 12

As figuras 13a e 13b mostram as formas "simétricas" da rede logarítmica com fusão preliminar e da rede logarítmica com separação preliminar. Seus exemplos mostram a possibilidade fundamental de conectar n blocos com esse tipo de rede, dentro dos quais o número de nós de comutação visitados durante qualquer viagem será proporcional ao logaritmo do número de blocos na cidade.


fig. 13 a


fig. 13 b

Estimativa exata precisa
Até o momento, uma rica coleção de redes já foi acumulada com várias funções, dependendo do número médio de nós visitados durante a viagem e do número de pontos de endereço na cidade. No entanto, ainda não sabemos quão pequeno esse número pode ser, em princípio, para um determinado número de quartos. O limite inferior para seu valor pode ser obtido usando a abordagem de informações.

Na verdade, mesmo que uma determinada rede viária conecte n pontos de endereço e as necessidades de migração da população sejam de tal ordem que qualquer jornada, não importa onde tenha começado, tenha a mesma chance de terminar em qualquer lugar da cidade.

Para resolver o problema pretendido, geraremos uma mensagem informativa auxiliar, seguindo esta receita: por um longo período, coletaremos registros de todas as viagens que possuem um ponto fixo no início e, em ordem aleatória, escreveremos os endereços nos quais essas viagens terminaram. A mensagem resultante será uma sequência aleatória composta pelos nomes de n pontos de endereço da cidade.

Uma maneira de transmitir essa mensagem a Marte é primeiro codificar todos os nomes com palavras binárias do mesmo tamanho, transformando a mensagem original em uma sequência de zeros e uns e, somente então, enviar a sequência resultante através de um canal de comunicação digital. Como para codificação distinguível, o conjunto nSe os nomes binários do log de comprimento ₂ n forem necessários , o comprimento da mensagem digital será:

(número de registros) × log ₂ n caracteres.

O mais interessante é que, de acordo com a teoria da informação, independentemente do algoritmo de codificação usado, é simplesmente impossível transmitir a mesma mensagem em média com um número menor de caracteres binários.

Uma alternativa para transmitir diretamente os nomes codificados dos pontos de extremidade pode ser um método no qual, para cada viagem, é indicado em qual das possíveis direções virou sua rota na próxima bifurcação da estrada. De acordo com nossas suposições, todos os garfos da rede podem ser apenas o dobro, portanto, para indicar a direção em cada caso, é necessário exatamente 1 bit. Qualquer pessoa que tenha um mapa da cidade e saiba o ponto de partida, a cadeia de bits adotada será suficiente para rastrear cada rota e restaurar a sequência original de seus destinos. Se o número médio de garfos (nós de divisão) visitados durante uma viagem for x , o comprimento da mensagem binária com o novo método de codificação será: (número de registros) × x.

Como foi dito anteriormente, um novo método de codificação não pode ser mais eficiente que o método de transferência direta de endereço binário, portanto: (número de registros) × x ≥ (número de registros) × log ₂ n , de onde:

x ≥ log ₂ n .

Embora a última desigualdade tenha sido deduzida inicialmente para um grupo de viagens com um ponto de partida fixo comum, sua aparência se mostrou independente da escolha específica desse ponto, por isso temos o direito de estender o resultado imediatamente a todas as viagens na cidade, obtendo assim a primeira parte da estimativa desejada:

P1 ) Desde que cada nova jornada tenha a mesma chance de terminar em qualquer um de nNos pontos de endereço da cidade, o número médio de nós de divisão por rota não pode ser menor que log ₂ n .

Retrocedendo mentalmente o relógio, você tornará cada ponto final de viagem o ponto inicial e cada nó de divisão de rede binária será um nó de mesclagem binário. Esse pequeno truque permite que você obtenha automaticamente a segunda parte que falta da estimativa em P1:

P2 ) Desde que cada jornada concluída tenha chances iguais de começar em qualquer um dos n pontos de endereço da cidade, o número médio de nós de fusão por rota não poderá ser menor que o log ₂ n .

Se recordarmos a existência de uma rede logarítmica com mesclagem preliminar e de uma rede logarítmica com separação preliminar, obteremos imediatamente dois exemplos de redes ideais em termos do número de nós de comutação, que, em média, são visitados dentro deles durante uma viagem. Vamos ver se essa qualidade os ajuda a reduzir a intensidade das perdas de comutação geradas.

Custos de comutação em redes logarítmicas

Se compararmos as redes com a fusão e a separação preliminares, a primeira parecerá muito mais atraente devido à sua simplicidade. Infelizmente, essa simplicidade também tem um lado oposto da moeda: combinar todas as rotas em um fluxo contradiz a recomendação i1 , tornando-se assim uma causa potencial de grandes perdas de tempo. Uma rede com separação preliminar parece seguir as recomendações i1 - i3 , no entanto, a julgar pela Figura 13b, tende a aumentar rapidamente o número de arestas e nós de comutação usados. A última qualidade pode tornar as redes desse tipo muito caras para uso prático.

Analisaremos esses problemas com mais detalhes. Para começar, concordamos que a cidade está sujeita ao modelo de migração de acesso uniforme e que o fluxo de viagens gerado por qualquer um de seus pontos de endereço tem capacidade unitária.

Perdas em uma rede com fusão preliminar
Na Figura 14 você pode ver um diagrama de fluxos decorrentes dos arranjos indicados na rede com fusão preliminar.


fig. 14

Pareceu-me conveniente descrever a rede em sua forma unidirecional, implicando que cada ponto inicial e final, não assinado com os mesmos números, na verdade significa o mesmo ponto de endereço na cidade.

Com base no diagrama, calculamos a intensidade dos custos de comutação gerados na rede. Vamos começar com a metade esquerda, onde, através da árvore de endereços reversa, todas as rotas são coletadas em um fluxo. Cada nó de comutação nesta parte da rede representa o local onde duas rodovias unidirecionais se fundem em uma (Fig. 15).


fig. 15

Se, inicialmente, cada uma das estradas for carregada com eficiência, depois da unificação, não será necessário reduzir o número de faixas, como resultado, não haverá redução associada nos custos de troca.

Suponha que um fluxo de energia da unidade já seja suficiente para encher efetivamente a estrada em pelo menos duas faixas. Nesse caso, chegamos a uma conclusão bastante inesperada: a união de carros flui dentro da rede logarítmica com a mesclagem preliminar ocorre absolutamente "de graça", sem causar perdas temporárias.

Calcular os custos que surgem na metade direita certa não é muito mais difícil. Essa parte da rede é uma árvore de endereços direta, cada nó sendo uma bifurcação simétrica nas estradas que já estudamos. Quando a energia do fluxo incidente p intensidade emergindo na perda igual a forquilha ( α / 2 ν ) ⋅ p ² /2. A potência do fluxo que entra no garfo raiz é: n , portanto, a intensidade das perdas no nó raiz é: ( α / 2 ν ) ⋅ n ²/ 2 Em cada próxima geração da árvore de endereços, o número de garfos dobra e a potência do fluxo em execução neles é reduzida pela metade. Como resultado, a fórmula de perda dentro da árvore inteira terá a forma:

I _{t_div1} = ( α / 2 ν ) ⋅ (1/2) ⋅ [ n ² + 2 ( n / 2) ² + 4 ( n / 4) ² + ... + ( n / 2) ⋅ 2 ² ] =

( α / 2 ν ) ⋅ ( n / 2) ² [1 + 1/2 + 1/4 + ... + 2 /n ] ≈ ( α / 2 ν ) ⋅ n ²

Como a potência do fluxo de percurso gerado em conjunto por todos os pontos de endereço é n , os custos de tempo por viagem são em média ( α / 2 ν ) ⋅ n , mostrando assim uma linear dependência do tamanho da cidade.

Quando se trata de redes abstratas, é difícil fazer uma estimativa significativa da área das estradas que elas usam. Como uma medida alternativa da complexidade estrutural, a potência total de todos os fluxos laterais pode ser calculada. Conforme planejado, o valor resultante deve refletir o custo de recursos para a montagem de todas as trocas exigidas pela rede. Não posso dizer que, na prática, esse método sempre tenha uma boa interpretação, mas provavelmente poderei ter uma idéia aproximada da quantidade de trabalho que temos pela frente.

Dentro da rede logarítmica com mesclagem preliminar, os fluxos laterais estão presentes apenas na árvore de endereços direta e sua potência total para cada geração de nós é a mesma: n / 2. Log de árvore total ₂ ngerações de nós, portanto, uma nova maneira de avaliar a complexidade fornece uma estimativa da complexidade: O ( n log ₂ n ).

Rede logarítmica com mesclagem preliminar
Número de pontos de endereço de energia da unidade ........................................ ............ n
Tempo médio de viagem
perdido devido a custos de mudança:
comportamento assintótico ........................ .................................................. ............................ O ( n )
valor exato ................ .................................................. ........................... ( α / 2 ν ) ⋅ n
O número de nós de comutação ............................................... .................................. O ( n )
O número de nós de comutação, levando em consideração a potência dos fluxos laterais .... ............... O ( n log ₂ n )

Perdas na rede com separação preliminar
Vamos agora prosseguir com a análise da rede logarítmica com separação preliminar, assumindo novamente que a rede é usada para conectar pontos de endereço de unidade de energia na cidade de “acesso uniforme”.

A Figura 16 mostra um fragmento dele, consistindo em um ponto de endereço junto com as árvores de Endereço direta e reversa adjacentes a este ponto.


fig. 16

Primeiro, estimamos a intensidade das perdas de comutação geradas pelo fragmento.
A magnitude dos custos gerados pela separação de fluxo pode ser encontrado através da substituição na fórmula I _{t_div1} = ( α / 2 ν ) ⋅ n ² deduzida para árvore de endereço directa no exemplo anterior, em vez da N - unidade. De fato, as árvores de Endereço direto nas Figuras 16 e 14 têm a mesma profundidade e conduzem fluxos semelhantes em espessura ao longo de si ( _{aprox.similaridade significa a capacidade de obter um conjunto de valores multiplicando os valores de outro conjunto por um número fixo, para ilustrar, a similaridade entre triângulos em seus lados pode ser usada} ). Devido à dependência quadrática entre o valor dos custos de comutação decorrentes de um garfo separado e a potência do fluxo fornecido a ele, uma diminuição simultânea de todos os fluxos em n vezes reduzirá as perdas na árvore inteira em n ² vezes, portanto, em vez do antigo ( α / 2 ν ) ⋅ n ² nós obtemos um valor igual a:

I _{t_div2} = ( α / 2 ν ).

Agora calculamos o valor dos custos na metade esquerda do fragmento.
Devido à pequenez dos fluxos combinados da estrada dentro da árvore de endereços reversa, desta vez não seria razoável construir mais do que duas faixas. As fusões nessas condições não custam mais: em contraste com o exemplo anterior, há pontos estreitos na rodovia (Fig. 17), onde os custos de troca serão necessários.


fig. 17

Supondo que o motorista esteja ciente do estreitamento próximo, podemos assumir que o processo de movimentação de carros da pista sem saída é lento, sendo esticado centenas de metros ao longo da rodovia. Nesse caso, temos o direito de recorrer ao truque que usamos anteriormente para calcular as perdas no garfo simétrico - dividir o fluxo total de migração q em muitas pequenas partes q _i e interpretar cada uma delas como uma corrente lateral do lado da rampa. As perdas geradas por cada sub- fluxo são calculadas pela fórmula:
I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s), no entanto, existem duas sutilezas.

A primeira delas é que os carros não migrarão além da próxima linha.
De fato: os fluxos nas duas faixas centrais, devido à simetria óbvia, devem sempre ter aproximadamente a mesma densidade, para que os motoristas não tenham muitos motivos para cruzar a linha do meio. A partir da observação feita que em perdas fórmula causadas por fluxo lateral parcial, s é igual a 1.

Assim que o carro deixando a banda extremo reconstruído nas duas filas centrais, taxa de fluxo no interior das tiras centrais está a aumentar gradualmente, em cada caso, variando a partir de P / 2 a P . Assim, a segunda sutileza é uma dependência significativa de pdo número do sub-fluxo i , o que nos obriga a não escrever:

I _i = ( α / 2 ν ) ⋅ p q _i ⋅ (1 + 1 / s ),
mas:
I _i = ( α / 2 ν ) p ( i ) ⋅ q _i ⋅ (1 + 1 / s ).
No caso em que muitas pequenas partes nas quais o fluxo de migração foi dividido tinham tamanho igual, a dependência p ( i ) é expressa por um gráfico linear (Fig. 18)


fig. 18

Para calcular a intensidade das perdas totais, é preciso recorrer à integração ou (isso torna possível uma forma particularmente simples de uma função integrável), pois p ( i ) assume o valor médio no gráfico igual a 3 P / 4. Como o fluxo total de migração do lado de cada faixa extrema é P / 2, a intensidade das perdas em uma fusão separada será:

Eu _mesclar = 2 ⋅ ( α / 2 ν ) ⋅ (3 P / 4) ⋅ ( P / 2)

= ( α / 2 ν ) 3 P ²/ 4

Para encontrar uma perda temporária gerado em uma faixa em inverter a árvore de endereços aplica-se a fórmula I _{de intercalação} para cada nó é a seguinte:

I _{t_merge} = (3/4) ⋅ ( α / 2 ν ) [1 ⋅ (1/2) ² + 2 ⋅ (1/4) ² + 4 ⋅ (1/8) ² + ... + ( n / 2) ⋅ (1 / n ) ² ] ≈

≈ (3/4) ⋅ ( α / 2 ν ) [1/4 + 1/8 + 1/16 + ...] =

= (3/8)⋅ ( α / 2 ν ) [1/2 + 1/4 + 1/8 + ...] =

= (3/8) ⋅ ( α / 2 ν ).

Os custos totais incorridos no fragmento devido à mesclagem e separação dos fluxos serão:

I _{t_merge} + I _{t_div2} = ( α / 2 ν ) [1 + 3/8] = 11/8 ( α / 2 ν ).

Uma rede logarítmica dividida preliminar contém apenas n tais fragmentos e exatamente nOs fluxos unitários são gerados por seus pontos de endereço; portanto, o valor que acabamos de encontrar é igual às perdas de comutação que ocorrem em média por viagem.

De fato, é mais importante para nós nem mesmo um número específico, que é igual aos custos específicos de troca, mas o fato de que esses custos permanecem constantes com o aumento de n . A última circunstância torna a rede logarítmica com separação preliminar assintoticamente a mais econômica em relação às perdas de comutação, entre todos os tipos de redes que estudamos anteriormente.

Infelizmente, a liderança não custa "de graça". Apesar do tamanho extremamente pequeno do grande número de fluxos, cada árvore de endereços incluída na rede contém cerca de 2 nnervuras de estrada de duas faixas e aproximadamente n nós de comutação em tamanho normal. Existem 2 n árvores na rede , o que significa O ( n ² ) bordas e nós, o que o torna não apenas o mais econômico no tempo, mas também a rede mais cara para construir, entre todos os exemplos considerados.

Quanto à soma dos fluxos laterais, seu valor, como é fácil de calcular, cresce com a velocidade O ( n log2 n ) e, nesse caso, não tem muito significado.

Rede logarítmica com separação preliminar
Número de pontos de endereço de energia da unidade ........................................ ............ n
Tempo médio de viagem,
Perda devido a custos de troca:
assintóticos .......................................... .................................................. .......... O (1)
valor exato .................................. .................................................. ........... 11/8 ( a / 2 v ).
O número de nós de comutação ............................................... .................................. O ( n ² )
O número de nós de comutação, levando em consideração a potência dos fluxos laterais ... ................ O ( n log ₂ n )

Rede logarítmica balanceada

Perdas de comutação excepcionalmente pequenas, com o possível uso da rede logarítmica com separação preliminar, mas ao mesmo tempo muito intensivas em recursos para sua construção, causam o desejo de encontrar uma maneira de mudar seu design para que o consumo de recursos seja reduzido significativamente e os custos de comutação não aumentem significativamente.

Obviamente, o principal culpado por um número excessivamente grande de estradas na rede é a eficiência extremamente baixa de seu uso. O último pode ser visto claramente na Figura 19, que mostra um diagrama detalhado dos fluxos dentro de uma árvore de endereços direta adjacente ao i- ésimo ponto de endereço.


fig. 19

No diagrama, o número acima da borda da árvore indica a potência do fluxo de percurso que passa ao longo da borda e o intervalo abaixo é o conjunto de pontos de endereço entre os quais esse fluxo será finalmente distribuído. Acredita-se que todas as arestas presentes no diagrama sejam rodovias de duas faixas; o número de arestas em cada geração da árvore é indicado na parte inferior da figura.

Após uma análise cuidadosa, você pode observar que a regra pela qual o fluxo de percurso é dividido em um nó específico é determinada exclusivamente pela posição desse nó na Árvore de Endereços e não depende do número do ponto de endereço que deu origem a esses disparos.

Se houver vários fluxos endereçados ao mesmo conjunto de pontos, e cada um deles não for poderoso o suficiente para preencher seu caminho alocado, por que não combiná-los em uma rodovia? De fato, essa idéia essencialmente simples permite construir uma boa rede abstrata, gerando perdas de comutação relativamente pequenas e econômica no número de estradas utilizadas.

Voltando à árvore de endereços do i- ésimo ponto, vemos que o fluxo que entra no nó raiz é dividido em dois fluxos-filhos com capacidade de 1/2 cada. O primeiro fluxo de enteado consiste em viagens endereçadas a pontos do intervalo [1; n / 2], o segundo - viaja endereçado a pontos do intervalo [( n / 2) + 1;n ]
Seguindo a idéia descrita acima, combinamos o mesmo tipo de fluxo de enteado em cada ponto ímpar e o próximo ponto de endereço com um número par seguindo-o em ordem. Essa técnica permite que cada par de pontos selecionado tenha, em vez de quatro fluxos, com uma potência de 1/2, apenas dois fluxos de magnitude unitária (Fig. 20). Daremos a abreviação BN ₂ [i; eu +1].


fig. 20

Se os fluxos dos enteados não fossem combinados, mas ainda estivessem dentro da árvore Address, na próxima geração de nós alcançados, cada um deles seria novamente dividido em duas partes, iguais em potência e tamanho dos conjuntos de pontos aos quais componentes de suas viagens.

Por que quebrar a tradição estabelecida, porque após a unificação, ainda temos o mesmo conjunto de tipos de fluxo de antes, mas com apenas menos representantes de cada tipo? - aplicável a cada um dos fluxos de saída BN ₂ [i; i +1] exatamente a mesma regra de separação que se aplicaria a um fluxo de seu tipo dentro da árvore de endereços.

Não há razão para que a construção lógica descrita acima para combinar e dividir os mesmos fluxos não possa ser repetida indutivamente. A Figura 21 mostra um diagrama da combinação de dois fragmentos de
BN ₂ em um fragmento de BN ₄ e a figura 22 mostra como o algoritmo se parece no caso geral.


fig. 21


fig. 22

No final, o processo de ampliação da fragmentação será concluído e nos levará ao único elemento BN _n [1; n ], chamaremos de rede balanceada do tipo logarítmico (Fig. 23).


fig. 23

Vamos examinar esta rede quanto à complexidade e magnitude das perdas de comutação geradas.
Com base na natureza indutiva do procedimento de construção da Rede Balanceada, o número de nós de comutação incluídos em sua estrutura pode ser descrito pela equação de retorno:

nós (BN _k ) = 2 nós (BN _{k / 2} ) + 2 k ,

com a condição de contorno:

nós (BN ₁ ) = 0. A

solução para este sistema de equações é a função:

nós (BN _n ) = 2 n log ₂ n .

Desde a construção do BN _nSe as etapas do log ₂ n de indução forem necessárias , cada jornada passará pelos nós de separação do log ₂ n e pelo mesmo número de nós mesclados, alternando-os em seu caminho (Fig. 24).


fig. 24

As perdas gerado no interior de cada montagem de separação:
( α / 2 ν ) ⋅ (1) ² /2.

As perdas gerados dentro de cada nó de fusão:
( α / 2 ν ) ⋅ 3 ⋅ (1/2) ² /4 3/16 = ( α / 2 ν ).

Dado que ambos na Rede Balanceada são n log ₂ n , obtemos o valor exato das perdas totais de comutação:
11/16 ( α / 2 ν ) n log ₂ n ,

que por uma viagem é:
11/16 ( α / 2 ν ) log ₂ n

Rede balanceada do tipo logarítmico
Número de pontos de endereço de energia da unidade ................... ................................. n
Tempo médio de viagem
perdido devido a custos de mudança:
comportamento assintótico ... .................................................. ................................................. O (log ₂ n )
valor exato ........................................... .................................................. ..11 / 16 ( α / 2 ν ) log₂ n
Número de nós de comutação ............................................. .................................... O ( n log ₂ n )
O número de nós de comutação, levando em consideração a potência do lado threads ................... O ( n log ₂ n )

Os números encontrados acima permitem que a Rede Balanceada seja considerada um bom compromisso entre a quantidade de perda de tempo introduzida e a complexidade estrutural geral. Seu uso como rede viária de uma cidade real é, em princípio, possível, mas dificilmente economicamente viável. Parece-me que a área em que o uso da Rede Balanceada pode realmente ser de grande benefício são os sistemas de informação em larga escala com requisitos rigorosos para a quantidade de atraso do sinal, como comunicações celulares, Internet, computação distribuída, computadores multiprocessadores. Para nós, o principal valor da Rede Balanceada é o método pelo qual ela foi construída. Um pouco mais tarde, usando uma modificação desse método, poderemos melhorar as redes de Centros Lineares e Celulares que são realmente importantes em termos práticos.

Por que cidades históricas estão condenadas a engarrafamentos

Minha afirmação pode parecer inesperada, mas a resposta para o motivo de cidades em desenvolvimento natural, geralmente sofrerem congestionamentos, já foi encontrada por nós nos parágrafos anteriores. Então, em que consiste?

O fato é que muitas cidades históricas que sobreviveram à era das fortalezas medievais (por exemplo, quase todas as capitais do “Velho Mundo”) herdaram dessa época a estrutura radial das ruas. Infelizmente (para os residentes modernos), uma rede de estradas com topologia semelhante não escala bem: a localização densa de estradas radiais perto do centro está se tornando muito rara na periferia. Como resultado, no processo de crescimento populacional, as ruas inicialmente localizadas à margem das poucas estradas que levavam à fortaleza se tornaram maiores e as ruas que apareceram na periferia eram curtas e não adquiriram significado de trânsito suficiente para crescer em largura. Como resultado, a rede de estradas que vemos agora nas grandes cidades históricas agora se refere mais frequentemente a sistemas de transporte do tipo arterial,e em nossa terminologia, ao tipo de redes logarítmicas com fusão preliminar (incompleta).


(Estradas de Moscou, foto: Stepanov Slava)

Se falarmos sobre a extensão do caminho que um motorista deve percorrer nas estradas, a implementação desse tipo de rede não é ruim: a distância percorrida geralmente difere pouco da distância em linha reta e seu valor médio na cidade, como deveria ser para sistemas de transporte "decentes", cresce à velocidade de O (√ n ). O problema é que, com a ampliação da cidade na rede logarítmica com uma fusão preliminar, os custos de troca gerados por ela aumentam muito rapidamente: a quantidade de tempo em que a viagem é prolongada, em média, devido a eles depende do número de pessoas que vivem na cidade como O ( n ) É claro que a partir de alguns n, esse tempo prevalecerá sobre o tempo puro para superar a distância; em outras palavras, os engarrafamentos aparecerão na cidade.

Sem dúvida, a reorganização do sistema de transporte nas grandes cidades históricas é uma tarefa que pode ser resolvida. No entanto, é importante entender aqui que a construção de outras duas, ou cinco grandes artérias de transporte, embora melhore ligeiramente a situação na cidade, mas a causa raiz dos engarrafamentos não será eliminada. Aparentemente, a única maneira de superar as deficiências da rede logarítmica com a fusão preliminar é usar outra rede. Um bom candidato aqui pode ser uma rede com topologias celulares, para a qual a taxa de crescimento do tempo para cobrir a distância, pelo menos, coincida com a taxa de crescimento das perdas de comutação.


(noite Berlim, foto: Vincent Laforet)

Talvez seja por isso que Berlim moderna, embora tenha grandes rodovias arteriais, já se distingue por uma estrutura de malha claramente visível.

Existem muitas soluções interessantes no mundo sobre como tornar os moradores das cidades históricas mais móveis, mas o principal prêmio na luta pela acessibilidade ao transporte provavelmente deve ser dado aos engenheiros de Barcelona.


(Rede rodoviária atualizada de Barcelona, ​​foto: Vincent Laforet)

Uma visão detalhada das redes de cidades lineares e celulares

Depois que os métodos de análise foram encontrados e refinados em redes abstratas, chegou a hora de aplicá-los a casos mais realistas de cidades com topologia Linear e Celular. Nesta seção, tentaremos analisar em detalhes os recursos de suas ligações de transporte, estabelecer o valor numérico da intensidade da perda de comutação, descobrir como seu valor depende do tamanho dos trimestres e discutir possíveis variações e melhorias.

Cidade linear
Desta vez, considere um exemplo de cidade na qual existem duas ruas de mão única: oeste com movimento norte e leste com movimento sul (Figura 25).


fig. 25

Deixe cada trimestre gerar um fluxo de curso da unidade de energia. Nesse caso, uma rota de viagem que leva de um bloco para outro representa 1 / n fluxo de tráfego .

Definimos para iniciantes o poder dos fluxos laterais nas rodovias. A oeste
da rua é a única maneira que você pode obter para o trimestre com índice i dos
( n - i ) blocos deitado sobre ela para o sul, e a única maneira pela qual a partir trimestre i pode alcançar os ( i - 1) quarteirões ao norte localizado dele . Daqui resulta que a capacidade dos fluxos de troca de tráfego entre a Rua Zapadnaya e o i- trimestre é igual a:

q _{W_out} = ( n - i ) / n - para o fluxo lateral que sai da West Street,
q _{W_in} = ( i - 1) / n - para o fluxo lateral adjacente ao tráfego nele. É claro que os fluxos laterais de alimentação em East Street depender de i maneira simétrica:
q _{E_out} = ( i - 1) / N - poder sair,
q _{E_in} = ( n - i ) / n - poder adjacente ao movimento em East Street lateral .

Obviamente, a soma dos fluxos que saem do i - ésimo quarto:

q _{E_in} + q _{W_in} = ( n - 1) / n ,
coincide com a soma dos fluxos que entram nele:
q _{E_out} + q _{E_out} = ( n - 1) / n ,
e ambos os valores não dependem de i de forma alguma (cada trimestre tem um fluxo de viagem de 1 / n de magnitude , que começa e termina dentro de si).

Para descobrir a potência dos fluxos principais, desenhe uma linha imaginária através da Western Highway no mesmo nível que euquarto trimestre. No total, essa linha será cruzada por:
(o número de quartos a partir de baixo) × (o número de quartos a partir de cima) = ( n - i ) ( i - 1) das rotas criando juntos um fluxo de magnitude:

P _W ( i ) = ( n - i ) ( i - 1 ) / n .

A mesma fórmula:
(número de quartos abaixo) × (número de quartos acima) / n , a
potência P _E do fluxo de tráfego na rua Vostochnaya deve ser expressa , em outras palavras:

P _E ( i ) = P _W( i ) = P ( i ).

Conhecendo o poder dos principais e secundários correntes, pode-se calcular a perda de intensidade que ocorrem na rede na área próxima ao i bloqueio -ésimo:

I ( i ) = ( α / 2 ν ) ⋅ P ( i ) ⋅ [( q _{E_in} + q _{W_in} ) ⋅ (1 + 1 / s ) + ( q _{E_out} + q _{E_out} ) ⋅ ( _1-1 / s )] =
= ( α / 2 ν ) ⋅ P ( i ) ⋅ [( 1-1 / n ) ⋅ (1 + 1 / s ) + ( 1-1 / n ) ⋅ ( 1-1 / s )] =
= ( α / 2 ν ) ⋅ 2 P ( i ) ⋅ ( 1-1 / n ) =
= 2 ( α / 2 ν ) ⋅ ( 1-1 / n ) ⋅ ( n - i) ( i - 1) / n =
= 2 ( α / 2 ν ) ⋅ (1 - 1 / n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ).

Se somarmos a última expressão sobre i , obteremos a intensidade das perdas geradas por toda a rede como um todo.

I = I _i I ( i )
= 2 _i 2 ( α / 2 ν ) ⋅ ( 1-1 /n ) ⋅ ( n - i ) ⋅ ( i - 1) ⋅ (1 / n ) =
= 2 ( α / 2 ν ) ⋅ ( 1-1 / n ) ⋅ n ² ⋅ ∑ _i (1 - i / n ) ⋅ ( i / n - 1 / n ) ⋅ (1 / n )
≈ 2 ( α / 2 ν ) ⋅ n ² ⋅ Σ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ).

A soma ∑ _i ( i / n ) ⋅ (1 - i / n ) ⋅ (1 / n ) para qualquer n grandepode ser substituída com boa precisão pela integral:

∫ t (1 - t ) d t ( t ∈ [0; 1]) = 1/2 - 1/3 = 1/6.

O que implica que a intensidade das perdas de comutação na distância linear de n blocos de capacidade da unidade de:

I = ( α / 2 ν ) n ² /3.

Até esse momento, consideramos apenas exemplos nos quais trimestres sempre geravam fluxos de unidade de energia. Vamos ver se a fórmula para as perdas de comutação da cidade linear muda se não houver uma única fonte de energia unitária para cada trimestre, mas - λ (os trimestres se tornarão λ vezes maiores).

Pegue uma cidade com m quarteirões. Se os quartos gerados fluírem 1, as perdas de comutação seriam ( α/ 2 ν ) m ² /3. Aumentar cada curso de produção de energia trimestre em X vezes leva a um aumento na λ e o principal e lateral fluxos simultaneamente, assim que o custo em cada junção, e meios dentro da rede como um todo aumenta em X ² vezes, e a perda de fórmula assume a forma:

I = ( α / 2 ν ) m ² ⋅ X ² /3.

Em geral, não importa como as perdas de comutação dependem do número de quartos na cidade, o principal para nós é como elas dependem do fluxo de energia de todas as viagens geradas dentro dela, ou seja, do número n de fontes de energia unitárias. Neste caso, n é igual a m ⋅ X , por conseguinte,:

I = ( α / 2 ν ) m ² ⋅ X ² /3 =
= ( α / 2 ν ) ( m ⋅ X ) ² /3 =
= ( α / 2 ν) N ² /3.

Em outras palavras, as perdas de comutação na cidade linear não dependem da pequenez de sua divisão em quartos.

Cidade celular
Imagine uma cidade celular na qual as estradas perpendiculares entre si estão espaçadas em diferentes alturas. Isso é possível, por exemplo, se todas as ruas que conduzem de norte a sul forem erguidas em pontes e as estradas que se estendem de oeste a leste forem construídas na superfície da Terra. Se, além disso, todas as ruas tiverem tráfego de mão dupla, o mapa de estradas dessa cidade será encaminhado para a Topologia Celular Padrão (Fig. 26).

O objetivo aqui, é claro, não é colocar em prática a rede descrita acima: ela não pareceria muito esteticamente agradável no contexto da paisagem da cidade e, além disso, devido à necessidade de intercâmbios em vários níveis, consumiria boa metade do espaço da rua. No entanto, essa rede puramente hipotética é uma boa maneira de obter as estimativas necessárias, que mais tarde podem ser facilmente estendidas a redes de estradas realmente interessantes do ponto de vista de sua aplicabilidade em cidades reais.

Como sempre, presumiremos que as necessidades de migração dos residentes sejam descritas pelo modelo de “acesso uniforme” e iniciaremos nossa consideração com o caso em que a capacidade de todos os fluxos de viagens gerados por um trimestre separado seja 1.

No exemplo da Cidade Celular Padrão, é conveniente se afastar da tradição estabelecida e considerar o ponto de endereço não como um bairro separado, mas como uma zona territorial de forma quadrada, que captura a interseção das rodovias e um quarto de todos os bairros adjacentes a ela. A Figura 27 mostra o posicionamento relativo de várias dessas zonas e mostra um padrão de tráfego dentro de uma delas. Este diagrama mostra claramente que qualquer motorista, saindo do trimestre, tem a oportunidade de entrar na estrada, seguindo na direção de qualquer uma das quatro partes do mundo.


fig. 26

Para descobrir o valor dos custos de troca gerados pela cidade, calculamos a potência de todos os fluxos principais e laterais em cada uma de suas zonas territoriais. A forma e a disposição mútua das zonas nos permitem recorrer a uma analogia do xadrez para resolver o último problema, considerando as zonas como células do campo e o movimento de carros entre elas - os movimentos do barco (Fig. 27). De uma célula para outra, desde que estejam em uma “posição geral” uma para a outra, a torre pode ser movida em dois movimentos e, se as duas células estiverem na mesma horizontal ou em uma vertical, em uma.


fig. 27

Para evitar muitas reservas inconvenientes, assumimos que o movimento em que a torre não se move para lugar algum também é permitido de acordo com nossas regras. A rota de movimento da torre, composta por dois movimentos, um dos quais é necessariamente realizado verticalmente e o outro horizontalmente, é chamado de mais simples. É razoável considerar a mudança "no lugar", tanto vertical como horizontal ao mesmo tempo. Nesse caso, a afirmação é verdadeira de que duas células no painel são conectadas uma à outra por exatamente duas rotas mais simples.

Para os motoristas, a rota "mais simples" é a maneira mais fácil de obter interferência mínima de uma zona territorial para outra, portanto, é razoável supor que viagens reais ocorrerão ao longo de linhas de rota elementares. De acordo com o modelo de “acesso uniforme” gerado pelo ponto de endereço (zona territorial), o fluxo de energia da unidade deve ser igualmente distribuído entre todos os n = d ² pontos de endereço da cidade, portanto, a capacidade do fluxo de viagem que passa ao longo de uma rota é 1 / (2 n ).

Calculamos o fluxo de qual magnitude passa através da célula ( i , j ) na direção do sul para o norte. A rota mais simples atravessa a célula (i , j ) de sul a norte em apenas duas situações. O primeiro deles (Fig. 28 à esquerda):

1a) a célula inicial da rota está localizada em uma das últimas ( d - i ) linhas de contorno (linhas);
2a) o ponto final da rota é uma das primeiras ( i - 1) células da j- ésima vertical (coluna);
3a) a rota começa com uma seção horizontal ou fica inteiramente dentro da j- ésima coluna.


fig. 28.

As condições que descrevem a segunda situação parecem simétricas (Fig. 28 à direita):

1b) o ponto de partida da rota é uma das últimas ( d - i ) células da j - ésima vertical;
2b) a célula final da rota está em uma das primeiras ( i - 1) linhas de contorno
3b) a rota começa com uma seção vertical ou fica inteiramente dentro da j- ésima coluna.

Há apenas 2 × [ d ⋅ ( i - 1) + 1 ⋅ ( i - 1)] × ( d - i no campo de xadrez) adequado para os requisitos das rotas mais simples, que juntos criam um fluxo com capacidade:

P _SN ( i , j ) = ( d + 1) ⋅ ( i - 1) ⋅ ( d - i ) / n (= P _SN ( i )).

Fixando j , obtemos a função

( P _SN ) _j ( i ) = P _SN ( i , j = Const),

descrevendo a dependência do poder do córrego que se move para o norte ao longo da j- ésima estrada vertical, na distância até o limite superior da cidade, medido em células.
Existem várias observações mais ou menos óbvias sobre as funções ( P _SN ) _j ( i ), vamos discuti-las.

Vamos começar com as circunstâncias, o que seria difícil para ignorar: P _SN ( i , j ) é praticamente independente do segundo argumento. Como resultado, as funções ( P _SN ) _j ( i ) = P _SN ( i) têm a mesma forma para todos os valores de j , ou seja, a posição específica da rua dentro da cidade celular não afeta sua carga de forma alguma. Formalmente, a última afirmação é comprovada apenas para a rodovia que leva ao norte, mas devido às simetrias da cidade, ela também se aplica automaticamente à rodovia de outras direções.

Agora, vejamos a fórmula em si para P _SN ( i ):

( d + 1) ⋅ ( i - 1) ⋅ ( d - i ) / (2 n ).

Como vemos, toda a dependência de P _SN em iestá na expressão ( i - 1) ⋅ ( d - i ). Essa expressão pode ser interpretada como o produto dos comprimentos dos intervalos direito e esquerdo nos quais o segmento inteiro de comprimento d se divide depois que o i- ésimo elemento é eliminado (Fig. 29a).


fig. 29a


fig. 29b

É claro que se você alterar “direita” para “esquerda” e “esquerda” para “direita” (Fig. 29b), o resultado do trabalho permanecerá o mesmo. De uma observação tão simples, em essência, existem duas conclusões que são muito úteis para nós:

1. P _SN ( i ) i = ( d + 1)/2, , Δ , Δ .
2. - , ( P _NS ) _j ( i ), j - , , - ( P _SN ) _j ( i ) i = ( d + 1)/2. ( P _SN ) _j ( i ) = P _SN ( i ), P _SN ( i ) i = ( d + 1)/2 , ( P _NS ) _j ( i ) = P _SN ( i ) = P _vert ( i ), , . P _SN ( i ) 30 (, d >> 1, i >> 1, d − i >> 1).

fig. 30

As potências dos fluxos principais ao longo das rodovias horizontais são facilmente encontradas usando simetrias rotacionais; formalmente, esse processo se resume a uma simples substituição de i por j em P _SN ( i ) e uma versão pequena do índice mais baixo.

A próxima coisa a fazer é encontrar o poder dos fluxos laterais. As viagens que fluem para dentro ou para fora do tráfego em uma estrada vertical dentro da célula ( i , j ) podem ser convenientemente divididas em quatro categorias:

1. fluir q _{in_transit} : inicial - qualquer célula i -simo horizontal finito - qualquer célula j -ésimo verticalmente, excepto para o ( i , j ) (Figura 31a);
2. q _{out_transit} : — j - , ( i , j ), — i - ( 31b);
3. q _in : — ( i , j ), — i - ( 31c);
4. q _out : — i - . — ( i , j ) ( 31d).

fig. 32: abcd Tendo

recontado o número de linhas de rota pertencentes a cada categoria separada, concluímos que as potências de todos os quatro fluxos são iguais e iguais:

q ₀ = d ⋅ ( d - 1) / (2 n )

Tendo os valores das potências dos fluxos principal e lateral em uma rodovia vertical, não é difícil calcular a quantidade de custos decorrentes da mudança. Dentro de uma única célula ( i , j ), os custos serão iguais a:

I _vert ( i , j ) = ( α / 2 ν ) ⋅ P _vert( i ) ⋅ [( q _in + q _{in_transit} ) ⋅ (1 + 1 / s ) + ( q _out + q _{out_transit} ) ⋅ ( _1-1 / s )]
= 4 ( α / 2 ν ) ⋅ ( d + 1) ( i - 1) ( d - i ) ⋅ d ( d - 1) / 2 n ² ≈
≈ 2 ( α / 2 ν) ⋅ d ⁵ ⋅ ( i / d ) (1 - i / d ) ⋅ (1 / d ) ⁴ =
= 2 ( α / 2 ν ) ⋅ d ² ⋅ ( i / d ) (1 - i / d ) ⋅ (1 / d ).

Para encontrar os custos incorridos nas ruas verticais de toda a cidade, precisamos somar I _vert ( i , j) Para ambos os índices:

Eu _vert = Σ _ij I _vert ( i , j ) =
= 2 ( α / 2 ν ) ⋅ d ² ⋅ Σ _ij ( i / d ) (1 - i / d ) ⋅ (1 / d ) .

Como a magnitude dos termos não depende de j de forma alguma , a soma do segundo índice é equivalente à multiplicação por d :

∑ _ij ( i / d) (1 - i / d ) ⋅ (1 / d ) = d ⋅ ∑ _i ( i / d ) (1 - i / d ) ⋅ (1 / d ).

A última soma pode ser aproximado pela integral familiar:

Σ _i ( i / d ) (1 - i / d ) ⋅ (1 / d ) ≈ ∫ t (1 - t ) d t ( t∈ [0; 1]) = 1/2 - 1/3 = 1/6.

O que implica que

eu _vert = ( α / 2 v ) ⋅ d ³ /3 = ( α / 2 v ) ⋅ n √ n / 3.

Para a questão de qual é o valor dos custos que eu _surgi em rodovias horizontais, usando a simetria da cidade, a resposta é:

I _horiz = eu _vert = ( α / 2 ν ) ⋅ n √ n / 3.

Assim, a intensidade de interrupção, as perdas no interior da célula padrão ao longo das cidades de rede é a seguinte:

I = I _vert + Eu _horiz = 2/3 ⋅ ( α 2 / ν ) ⋅ n √ n ,

e por viagem média custos cair valor

2/3 ⋅ ( α / 2 ν ) ⋅ √ n

Influência do tamanho da célula pela quantidade de perdas de comutação
Quartos que geram fluxos de energia unitária são uma limitação bastante artificial das condições do problema. Estendemos os resultados obtidos acima aos casos em que a potência do fluxo de percurso gerado por uma célula territorial é igual a λ .
Deixe a cidade consistir em m tais células. Se todas as células tivessem apenas uma unidade de potência, a intensidade das perdas totais de comutação seria I ₁ = 2/3 ⋅ ( α / 2 ν ) ⋅ m √ m . Um aumento no número de viagens feitas por λ vezes em λo tempo aumentará a potência de todos os fluxos principais e laterais das rodovias, o que por sua vez fará com que λ ² vezes aumente todos os custos de troca gerados na cidade. A nova fórmula para a intensidade das perdas assumirá a seguinte forma:

I = 2/3 ⋅ ( α / 2 ν ) λ ² ⋅ m √ m

Se assumirmos que a célula consiste em λ pontos de endereço da unidade de potência, o número total de tais pontos será: n = λ m . Vamos expressar I em função de n e λ :

I2/3 = ⋅ ( α / 2 ν ) λ ² ⋅ m √ m =
= 2/3 ⋅ ( α / 2 ν ) ⋅ √ λ ⋅ ( λ √ λ ) ⋅ ( m √ m ) =
= 03/02 ⋅ √ λ ( α / 2 ν ) ⋅ ( λ m ) √ ( λ m )
= 2/3 ⋅√ λ ( α / 2 ν ) ⋅ n √ n .

Os custos médios atribuível à viagem para as novas condições constituem 2/3 ⋅ √ X ( α 2 / ν ) ⋅ √ n , sendo no √ X vezes maior em comparação com o valor na sua compilado a partir de blocos individuais de energia.

A última fórmula nos diz que, para a mesma população, densidade populacional e área total de todas as estradas, o custo dos custos de troca é maior, quanto maiores os bairros na hora de projetar a cidade foram escolhidos por seu arquiteto. Caso a população da cidade esteja desigualmente distribuída em seu território, é claro que você deve prestar atenção não às dimensões geométricas, mas antes de tudo ao número médio de pessoas no trimestre e à atividade de migração.


(Foto do centro de Nova York: Vincent Laforet)

A observação acima é especialmente importante ao projetar áreas com edifícios arranha-céus. Devido à combinação de uma alta densidade populacional e de sua alta mobilidade, é desejável criar alojamentos em áreas de altitude várias vezes menores em tamanho do que o habitual para a construção de andares padrão. Nas civilizações, onde a construção de arranha-céus tem uma longa história, a prática de isolar até grandes edifícios separados como um bloco é generalizada.

Cidade celular de semáforo
Em cada caso, quando as linhas de duas ruas movimentadas se cruzam no mapa, o arquiteto deve fazer uma escolha: ou levante uma dessas estradas para a ponte, permitindo que o fluxo da outra passe livremente por baixo ou realize a interseção na forma de uma interseção regular e resolva o conflito de fluxo resultando em tráfego regulamento. A segunda opção atrai com sua simplicidade, a falta da necessidade de construir estruturas de engenharia em larga escala e, além disso, fornece uma maneira fácil de atravessar a rua para pedestres, por esses motivos nas cidades que costumam preferir.


(tarde do centro de Los Angeles, foto: Boris Shein)

O uso de semáforos em redes com topologia de célula possui características próprias. No capítulo 1, foi mostrado que, com a sincronização adequada dos semáforos, os carros, enquanto se deslocam pela mesma rua, nem precisam parar nos cruzamentos: um sinal verde sempre acenderá em sua direção. Esse tipo de fenômeno é geralmente chamado de regime de onda verde . Para criá-lo, os fluxos de tráfego precisam ser divididos em duas zonas alternadas de dois tipos: cheias de carros e livres delas. A seguir, é selecionado um modo de operação dos semáforos que, no período em que a próxima "porção" passa pelo cruzamento por uma das ruas, a porção anterior de carros que se deslocam pela rua perpendicular já passou por ela e o próximo ainda não chegou (Fig. 33).


fig. 33

A capacidade de direcionar tráfego no modo verde acarreta seus próprios custos e impõe certas restrições ao layout das ruas da cidade.

Olhando novamente para a Figura 33, é fácil ver que, a qualquer momento, exatamente metade da área de todas as estradas não é realmente usada. Para compensar o simples, na metade da estrada usada, a potência local dos fluxos de automóveis e o número de faixas necessárias para eles deve ser o dobro do que em uma cidade com viadutos.

A segunda circunstância mais importante associada ao uso de ondas verdes é a regulamentação estrita do tamanho permitido de quartos: seu comprimento (para ruas de mão dupla) deve ser múltiplo do comprimento da onda verde cheia (uma seção do córrego no qual é possível um movimento sem obstáculos), totalizando cerca de 500 metros. Conforme observado no parágrafo anterior, as áreas com alta densidade populacional exigem um aumento da frequência da localização das estradas, portanto, a restrição de baixo na distância entre as rodovias pode causar dificuldades no trânsito.

É interessante notar que, no modo de ondas verdes, as regras mudam levemente de acordo com as rotas de viagem que são trocadas dentro da rede. Por exemplo, a conexão de outro carro ao fluxo de tráfego principal em uma rodovia de rua pode ser realizada entre as zonas cheias, não causando assim sérios custos de troca (ponto “1”, Fig. 34a).


fig. 34

Obviamente, esse carro em si terá que perder algum tempo aguardando a zona vazia mais próxima antes de entrar na estrada e, depois disso, permanecer no sinal de trânsito até que a próxima zona cheia acerte (ponto "2" Fig. 34a). a magnitude dessas perdas não depende do tamanho da cidade ou da ocupação do tráfego nas ruas, para que possam ser negligenciadas em larga escala.

A situação é completamente diferente se um carro tenta deixar o tráfego na estrada (Fig. 34b). Aqui, com toda a probabilidade, já não há maneiras complicadas de reduzir as perdas de comutação criadas por ele. Além disso, devido à duplicação da potência local do fluxo dentro das zonas cheias, a remoção de um carro selecionado arbitrariamente custa um tempo que custa duas vezes mais do que em uma cidade com viadutos. No total, a “entrada” barata e a “saída” mais cara dos riachos compensam-se, fazendo com que a Cidade das Células de Semáforo nesse aspecto quase não seja melhor, mas não seja pior que a Standard.

Cidade celular unidirecional
Além de usar semáforos, há pelo menos mais uma oportunidade de fugir das trocas monstruosas da cidade padrão. Consiste em dividir espacialmente (Fig. 35) estradas com a direção oposta do movimento.


fig. 35

Como resultado dessas mudanças, o número de ruas dobrará, todas se tornarão unilaterais, mas o mais importante é que as trocas serão bastante simplificadas (Fig. 36).


fig. 36.
Como o número de rodovias que levam a cada uma das partes do mundo e o número de viagens que passam por elas permanecem os mesmos, as capacidades de todos os fluxos e, com elas, os custos de mudança na cidade de mão única e na cidade padrão com dois grandes quartos (lineares), devem combinar. Se compararmos as cidades Standard e Unilaterais com os mesmos tamanhos de trimestre, a segunda terá o dobro das perdas de troca.

Rua "linear".

Como as perdas de comutação podem ser reduzidas em uma rede celular? A resposta a esta pergunta nos permitirá selecionar com êxito a analogia e um pouco mais experiente.

Considere uma modificação um tanto incomum da Rede Celular, que implica que todas as rodovias que se estendem de oeste a leste são de mão dupla, enquanto que na perpendicular a elas as estradas são permitidas apenas de uma maneira: norte ou sul, e essas direções se alternam de rua em rua.

Como sempre, assumiremos que a cidade obedece ao modelo de acesso uniforme, e cada quarto dela gera um fluxo de viagens de energia condicionalmente unitária.

Nesse caso, parece plausível que o núcleo dentro do trimestre ( i , j) o fluxo de viagens, deixando-o, é distribuído entre as ruas mais próximas da seguinte maneira: 1/4 dela chega à estrada horizontal por cima, 1/4 mais à estrada horizontal por baixo, 1/4 ⋅ i / d flui para o norte ao longo da estrada vertical e
1/4 ⋅ (1 - i / d ) - ao longo da segunda estrada vertical para o sul (Fig. 37).

fig. 37.

De fato, de acordo com os algoritmos de construção de rotas discutidos anteriormente, de acordo com as estatísticas, metade das viagens começa em uma seção horizontal e, para os motoristas que preferem essa metade, em geral não importa se o caminho fica ao norte do trimestre ( i , j ) ou sul dele. A metade restante das viagens começará com uma seção vertical de tráfego e será dividida entre as rodovias sul e norte em relação ao número de quartos situados ( i , j ) ao sul até o número de quartos situados ao norte.

Quanto ao fluxo de viagem direcionado para dentro ( i , j), a regra de sua divisão em relação à rodovia que circunda o bairro será simétrica (Fig. 38).


fig. 38.

Entre os quatro cruzamentos adjacentes ao trimestre ( i , j ), consideramos separadamente os fluxos laterais no cruzamento da rodovia horizontal inferior e da rua vertical com tráfego para o norte (Fig. 38). Fluxo máquina inserindo uma horizontal para uma pré-visualização vertical é:
1/2 ⋅ (o número de blocos na horizontal) x (o número de blocos na vertical não inferior a ( i , j )) ⋅ 1 / d ² =
= 1/2 ⋅ d ⋅ i / d ² =
= 1/2 ⋅ i / d .
A magnitude do fluxo lateral na direcção oposta é:
1/2 ⋅ (o número de blocos na vertical, estritamente inferior a ( i , j )) x (o número de blocos na vertical) ⋅ 1 / d ² =
= 1/2 ⋅ ( d - i ) ⋅ d / d ² =
= 1/2 ⋅ (1 - i / d ).

Vamos agora voltar nossa atenção da Cidade Celular como um todo para qualquer uma de suas ruas verticais, vamos chamá-la de My_street. Devido a simetrias, não limitaremos nosso raciocínio se assumirmos que o movimento ao longo de My_street é direcionado de sul para norte (Fig. 39).


fig. 39.

A Figura 40 mostra os gráficos da potência dos fluxos principal e lateral na rodovia ao longo de My_street, que, como o leitor pode notar, são incrivelmente semelhantes a gráficos semelhantes para a rodovia de mão única de Linear City (Figura 26).



fig. 40.

Nesses exemplos, os diagramas de fluxo coincidem completamente se dentro de My_street os fluxos laterais relacionados a cada par de quartos opostos e a estrada horizontal abaixo deles são formalmente designados a uma célula territorial imaginária. Como pode ser visto nas tabelas anteriores, a rede rodoviária da cidade linear causa uma das maiores perdas de comutação entre as redes das arquiteturas que já estudamos. Deste ponto de vista, o padrão de tráfego em uma única rua da cidade celular parece extremamente ineficiente e é um elemento que deve ser tentado melhorar em primeiro lugar.

Rede avançada para cidade linear
E assim, somos confrontados com a tarefa de melhorar a Rede Linear para que ela não se torne uma "quadrada". A circunstância que apresenta a maior ineficiência na operação da Rede Linear é a unificação de todas as rotas em apenas dois fluxos de tráfego muito grandes. Nesta situação, um passo razoável seria dividir os fluxos ao longo de suas duas rodovias em Q partes iguais. Como os custos de tempo causados ​​por cada carro entrando ou saindo do tráfego são proporcionais à intensidade do tráfego, como resultado da divisão das linhas das ruas em Q partes isoladas (Fig. 41a), as perdas de comutação dentro da cidade Linear devem ter diminuído os tempos Q.


fig. 41

Apenas construir dez estradas próximas e esperar que os próprios motoristas estejam igualmente distribuídos entre eles - infelizmente, não parece ter nenhuma chance de sucesso. Uma decisão muito mais ponderada é projetar a rede para que cada estrada não conduza a todos os quadrantes, mas apenas a um pequeno “segmento” da cidade, onde seria difícil contorná-la (Fig. 41b).

Você pode ver uma idéia semelhante no esquema de movimentação de elevadores dentro de edifícios de vários andares. Lá, cada elevador permite entrar e sair não em todos os andares, mas apenas dentro de um certo intervalo de alturas. Tomando esse conceito, vamos olhar mais de perto a estrada r _k , que abre o acesso ao segmento Δ _k = ( x _k, x _{k +1} ] para viagens que começaram (de forma constante) ao sul de x _k (acredita-se que a numeração dos blocos seja feita de baixo para cima). No lado de cada trimestre, cujo número (estritamente) menos de x _k , a estrada r _{o k} entra no fluxo q _no poder | Δ _k | / n (1 / n cada endereço de cada quarto dentro de Δ _k ), ao mesmo tempo, assume-se que a capacidade de colapsar com r _kem direção a qualquer um dos trimestres mencionados, seja devido a regras de tráfego estabelecidas ou devido ao design especial da rede rodoviária.

Acumulado no intervalo [1, x _k ] carros, eventualmente, foram igualmente distribuídos entre os trimestres do delta _{do k} , por isso, se você não iria viajar para lá, o início eo fim dos quais se encontram dentro do delta _{do k} , o fluxo lateral q _{para fora} na direção de cada um dos blocos nesta área teria uma potência x _k / n (Fig. 42).


fig. 42.

De fato, a contribuição de "interno" viaja para a potência dos fluxos laterais também ocorre, no entanto, o valor dessa contribuição nunca excede | Δ _k | / n ; portanto, no caso em que x _k >> | Δ _k |, pode ser simplesmente negligenciado. A potência p _{k da} corrente principal ao longo de r _k com as simplificações feitas será representada por um gráfico de duas seções retas com um P _k máximo igual a x _k ⋅ | Δ _k | / n . O valor aproximado das perdas de comutação em r _k pode ser encontrado pela fórmula:

I _k = ( α / 2 ν ) ∑ _x [ q _in ( x ) ⋅ p _k ( x ) ⋅ (1 + 1 / s )] + ( α / 2 ν ) ⋅ _x [ q _out ( x ) ⋅ p _k ( x ) ⋅ ( 1-1 / s )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ∑ _x [| Δ _k | / n ⋅ p _k ( x )] + ( α / 2 ν ) ⋅ ( 1-1 / s ) ∑ _x [ x _k / n ⋅ p _k ( x )] =

= ( α / 2 ν ) ⋅ (1 + 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / x _k + ( α / 2 ν ) ⋅ (1 - 1 / s ) ⋅ ( x _k ⋅ | Δ _k | / n ) ⋅ ( ∑ _x p _k ( x )) / | Δ _k |,

onde a primeira soma é tomada sobre a área x ∈ [1, x _k ] e a segunda sobre x ∈ Δ _k . Expressões:

( P _x p _k ( x )) / x _k , x ∈ [1, x _k ] e

( P _x p _k ( x )) / | Δ _k |, x ∈ Δ _k

não há nada além da potência média do fluxo ao longo de _rk dentro dos intervalos indicados. Como o gráfico de potência dentro desses intervalos tem a forma de uma linha reta, a potência média em ambos os casos é P _k / 2. Substituindo
x _k ⋅ | Δ _k | / n ligado
P _k
finalmente damos a fórmula para a intensidade da perda à sua forma mais simples:

I _k = 2 ( α / 2 ν ) ⋅ P _k ⋅ P _k / 2 = ( α / 2 ν ) ⋅ P _k ²

Vamos agora tentar calcular a sequência x _{k dos} números daqueles trimestres pelos quais a cidade linear deve ser dividida em segmentos. Como critério para a seleção de segmentos, assumimos o requisito de que a potência máxima dos fluxos de tráfego P _k em estradas adequadas tenha o mesmo valor, independente de k , ou seja, a igualdade

x _k ⋅ | Δ _k = Const.

Lembrando que | Δ _k = x _{k + 1} - x _k , chegamos à equação da diferença:

x _{k + 1} - x _k = Const / x _k .

Assumindo x e k como variáveis ​​contínuas e substituindo

Dê sua _nota ! Dê sua nota !

em d x / d k ⋅ 1,

podemos aproximar a equação da diferença pelo diferencial:

d x / d k = Const / x <=> x d x = Const ⋅ d k .

De onde obtemos para x _{k uma} solução na forma geral:

x _k = C ₁ √ ( k + C ₂ ).

Resta determinar o valor das constantes C1 e C2 a partir das condições de contorno; no entanto, há uma sutileza importante nesse assunto. Diferentemente da situação nos demais segmentos, todos os carros que chegavam da rodovia oeste aos quartos do segmento no número 1, dentro do mesmo segmento, iniciaram sua jornada. Como resultado, o gráfico da potência de fluxo na primeira rodovia ao norte terá a forma de uma parábola invertida regular.

Ao mesmo tempo, as condições a priori das quais a fórmula para x _k foi obtida sugerem essencialmente que os gráficos da potência dos fluxos em todas as rodovias devem estar próximos de uma vista triangular, e as próprias jornadas devem começar principalmente fora do segmento para onde são direcionadas. Esses requisitos podem ser cumpridos com razoável precisão se dividirmos formalmente o primeiro segmento em duas partes iguais (a parábola é abordada por um triângulo isósceles e a maioria das viagens pela primeira estrada é de fato direcionada da metade sul do segmento número 1 para a metade norte), sem aumentar o número de estradas ( fig 43).


fig. 43

É o meio do primeiro segmento que deve ser considerado o ponto x ₁ na fórmula para x _k . A partir daqui, obtemos a primeira condição de contorno:

x ₂ = 2 x ₁ ou

√ (2 + C ₂ ) = 2 ⋅ √ (1 + C ₂ ) =>

C ₂ = - 2/3.

A segunda condição de contorno é obtida com a exigência de que as estradas e os segmentos sejam exatamente Q , o que significa que x _{Q + 1} deve ser igual ao próximo trimestre com o maior número na cidade:

C ₁ √ ( Q + 1 - 2/3) = n + 1, de onde

C ₁ ≈ ( n + 1) / √ Q.

Desta forma:

x _k ≈ ( n + 1) ⋅ √ ( k - 2/3) / √ Q ,

| Δ _k ≈ d x / d k = ( n + 1) / 2√ ( k - 2/3) ⋅ √ Q

P _k = x _k ⋅ | Δ _k | / n =

= ( n + 1) 2/2 n ⋅ Q ≈ n / 2 Q

I _k = ( α / 2 ν ) ⋅ P _k ² =

= ( α / 2 ν ) ⋅ ( n / 2 Q ) ² .

Como todas as rodovias de rua em 2 Q geram perdas da mesma intensidade, o valor dos custos de comutação em toda a rede como um todo será:

I = 2 Q ⋅ ( α / 2 ν ) ⋅ ( n / 2 Q ) ² = ( α / 2 ν ) ⋅ n 2/2 Q.

Como você pode ver, o desejado é alcançado: depois de dividir as principais rodovias em partes Q , as perdas realmente diminuíram por um fator de Q (exceto pelo coeficiente constante de 1/3 a 1/2 que aumentou em comparação com a fórmula da cidade linear usual). Bem, metade do trabalho está feito, resta aplicar o resultado para melhorar a cidade com a arquitetura Celular.

Elevador de arranha-céu na cidade de celular
Por simplicidade, nos contentaremos com um exemplo de cidade em que todas as ruas são de mão única. Usando a analogia entre a Cidade Linear e as ruas individuais da Cidade Celular, dividimos a estrada ao longo da última em partes Q. Por padrão, acredita-se que, saindo do trimestre, você pode pegar qualquer estrada que passa perto dele. Ao mesmo tempo, entre todas as rodovias ao longo de uma rua, há uma curva em direção a um bairro específico com exatamente uma delas. No processo de estabelecimento de regras, sua uniformidade e simplicidade são extremamente importantes. Veja a Figura 44:


fig. 44

todas as ruas têm a mesma aparência e as mesmas regras, qual de suas estradas em que bloco de contas abre acesso. A Figura 45 mostra um diagrama de curvas permitidas entre rodovias. Olhar para esta foto é difícil de não ficar confuso. O mesmo é dito frequentemente sobre o sistema de metrô em alguma cidade grande. No entanto, em ambos os casos, tudo se torna claro e simples se você souber a lógica da ideia. A regra lógica das curvas permitidas parece bastante simples: se você estiver dirigindo por uma estrada, você atravessa estradas perpendiculares ao seu movimento e pode entrar no quarteirão diretamente atrás delas, então pode entrar em qualquer uma dessas estradas.


fig. 45

A topologia do elevador de arranha-céu é compatível com semáforos e viadutos. É difícil, mas pode ser generalizado para redes não necessariamente de estrutura celular ou linear. Este último é realmente importante para cidades históricas, onde é improvável demolir metade dos monumentos históricos para estabelecer muitas pequenas ruas retas, mas nas quais já existem ruas bastante grandes que podem acomodar várias estradas de duas ou três faixas.

Sobre os problemas do transporte e o trabalho da matemática

É agradável concluir o minucioso trabalho semestral. O trabalho que escrevi, é claro, não resolve todos os problemas e dificuldades do projeto de estradas - esse negócio exige um grande número de pessoas muito diversas. No entanto, seus resultados oferecem uma oportunidade de ver erros importantes em cidades já construídas e fornecem métodos para evitar esses erros no futuro. Este artigo não foi concebido como um livro de referência, cobrindo todos os casos possíveis que um engenheiro pode encontrar na prática - considerei minha tarefa principal dar um novo ponto de vista, desenvolver uma nova maneira de raciocinar e falar sobre um problema, fornecer o mínimo necessário de exemplos de modelos simples, preparados pelo leitor já podia me expandir.

Fica triste quando você percebe quanto tempo foi perdido pelos moradores da cidade em engarrafamentos, apenas porque na hora certa não havia matemático que pudesse passar a noite em um problema completamente solucionável. Quantos desses problemas ainda cercam nossa vida ou ocultam sua profissão? Existe uma pessoa sentada perto de você no trabalho cujas ferramentas têm um lápis e uma folha de papel?

Espero que tudo mude para melhor.

Obrigado pela atenção e boa sorte!
Sergey Kovalenko.

2019 ano
magnolia@bk.ru


(Foto: Vincent Laforet)