Abordagem gananciosa e máquinas caça-níqueis. Análise das tarefas da pista ML do campeonato de programação

Continuamos a publicar análises das tarefas propostas no campeonato recente. Em seguida, são realizadas tarefas da rodada de qualificação para especialistas em aprendizado de máquina. Esta é a terceira faixa de quatro (back-end, front-end, ML, análises). Os participantes precisavam criar um modelo para corrigir erros de digitação nos textos, propor uma estratégia para jogar em máquinas caça-níqueis, lembrar um sistema de recomendações de conteúdo e compor vários outros programas.

A. Erros de digitação

Condição

(epígrafe) (de um fórum)
- Quem compôs esse absurdo?
Astrofísicos. Eles também são pessoas.
- Você cometeu 10 erros na palavra "jornalistas".

Muitos usuários cometem erros de digitação, alguns por pressionar teclas e outros por causa de analfabetismo. Queremos verificar se o usuário realmente pode ter em mente alguma outra palavra além da que ele digitou.

Mais formalmente, suponha que ocorra o seguinte modelo de erro: o usuário começa com uma palavra que deseja escrever e, posteriormente, comete vários erros. Cada erro é uma substituição de alguma substring da palavra por outra substring. Um erro corresponde à substituição apenas em uma posição (ou seja, se o usuário deseja cometer um único erro pela regra “abc” → “cba”, a partir da cadeia “abcabc” ele pode obter “cbaabc” ou “abccba”). Após cada erro, o processo se repete. A mesma regra pode ser usada várias vezes em etapas diferentes (por exemplo, no exemplo acima, “cbacba” pode ser obtido em duas etapas).

É necessário determinar o número mínimo de erros que um usuário poderia cometer se tivesse em mente uma determinada palavra e escrevesse outra.

Solução

Vamos tentar gerar a partir da ortografia correta todas as palavras possíveis, com no máximo 4 erros. No pior dos casos, pode haver O ((L﹒N) ⁴ ). Nas limitações do problema, esse é um número bastante grande, portanto, você precisa descobrir como reduzir a complexidade. Em vez disso, você pode usar o algoritmo meet-in-the-middle: gere palavras com não mais que 2 erros, bem como palavras com as quais você pode obter uma palavra escrita pelo usuário com não mais que 2 erros. Observe que o tamanho de cada um desses conjuntos não excederá 10 ⁶ . Se o número de erros cometidos pelo usuário não exceder 4, esses conjuntos se cruzarão. Da mesma forma, podemos verificar se o número de erros não excede 3, 2 e 1.

 struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; } 

B. Bandido de muitas armas

Condição

Esta é uma tarefa interativa.

Você mesmo não sabe como aconteceu, mas se viu em um salão com máquinas caça-níqueis com um saco inteiro de fichas. Infelizmente, nas bilheterias, eles se recusam a aceitar os tokens de volta e você decidiu tentar a sorte. Existem muitas máquinas caça-níqueis no salão que você pode jogar. Para um jogo com uma slot machine, você usa um token. Em caso de vitória, a máquina oferece um dólar, em caso de perda - nada. Cada máquina tem uma probabilidade fixa de ganhar (que você não conhece), mas é diferente para máquinas diferentes. Tendo estudado o site do fabricante dessas máquinas, você descobriu que a probabilidade de ganhar para cada máquina é selecionada aleatoriamente no estágio de fabricação a partir da distribuição beta com determinados parâmetros.

Você deseja maximizar seus ganhos esperados.

Solução

Este problema é bem conhecido, poderia ser resolvido de diferentes maneiras. A principal decisão do júri implementou a estratégia de amostragem Thompson , mas como o número de etapas era conhecido no início do programa, existem estratégias mais ótimas (por exemplo, UCB1). Além disso, pode-se conviver com a estratégia epsilon-gananciosa: com uma certa probabilidade ε toca uma máquina aleatória e com uma probabilidade (1 - ε) toca uma máquina com as melhores estatísticas de vitória.

 class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self._bs = [init_b] * self.n # [random.betavariate(self.alpha, self.beta) for _ in range(self.n)] self.last_move = -1 random.seed(int(time.time())) def move(self): samples = [random.betavariate(self._as[x], self._bs[x]) for x in range(self.n)] self.last_move = max(range(self.n), key=lambda x: samples[x]) self.moves.append(self.last_move) return self.last_move def set_reward(self, reward): i = self.last_move r = reward self._as[i] += r self._bs[i] += (1 - r) return i, r while True: n, m = map(int, sys.stdin.readline().split()) if n == 0 and m == 0: break alpha, beta = map(float, sys.stdin.readline().split()) solver = ThompsonSampling(m) for _ in range(n): print >> sys.stdout, solver.move() + 1 sys.stdout.flush() reward = int(sys.stdin.readline()) solver.set_reward(reward) 

C. Alinhamento das frases

Condição

Uma das tarefas mais importantes para o treinamento de um bom modelo de tradução automática é um bom caso de frases paralelas. Normalmente, a fonte de ofertas paralelas são documentos paralelos. Acontece que, muitas vezes, para construir um certo corpus de frases paralelas, você não precisa saber nada além de seus comprimentos. Em particular, você pode notar que, quanto mais longa a frase no idioma de origem, mais provavelmente será traduzida. Alguma dificuldade reside no fato de que, durante a tradução, o número de frases no texto pode mudar: algumas vezes duas frases adjacentes na tradução podem ser combinadas em uma ou vice-versa - uma frase pode ser dividida em duas. Em alguns casos raros, as frases podem ser omitidas inteiramente em uma tradução ou uma tradução pode aparecer em uma tradução que não estava no original.

Mais formalmente, suponha que o seguinte modelo generativo para gabinetes paralelos seja verdadeiro. Em cada etapa, fazemos um dos seguintes:

1. Pare

Com probabilidade p _{h, a} geração dos cascos termina.

2. [1-0] Ignorando ofertas

Com probabilidade p _d, atribuímos uma frase ao texto original. Não atribuímos nada à tradução. O comprimento da frase no idioma original L ≥ 1 é selecionado a partir da distribuição discreta:

.

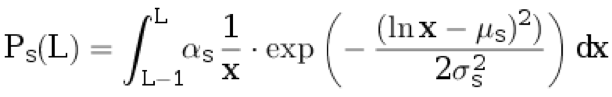
Aqui μ _s , σ _s são os parâmetros de distribuição e α _s é o coeficiente de normalização escolhido para que .

3. [0-1] Inserir proposta

Com probabilidade p _i, atribuímos uma frase à tradução. Não atribuímos nada ao original. O comprimento de uma frase em um idioma de tradução L ≥ 1 é selecionado a partir de uma distribuição discreta:

.

Aqui μ _t , σ _t são os parâmetros de distribuição e α _t é o coeficiente de normalização escolhido para que .

4. Tradução

Com probabilidade (1 - p _d - p _i - p _h ), tomamos o comprimento da sentença no idioma original L _s ≥ 1 da distribuição p _s (com arredondamento para cima). Em seguida, geramos o comprimento da sentença no idioma de tradução L _t ≥ 1 a partir da distribuição discreta condicional:

.

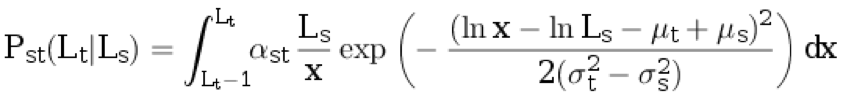
Aqui, α _st é o coeficiente de normalização, e os demais parâmetros são descritos nos parágrafos anteriores.

O próximo passo é outro:

1. [2-1] Com probabilidade p _{dividida s, a} sentença gerada no idioma original se divide em duas não vazias, de modo que o número total de palavras aumenta exatamente uma . A probabilidade de uma sentença de comprimento L _s se dividir em partes do comprimento L ₁ e L ₂ (isto é, L ₁ + L ₂ = L _s + 1) é proporcional a P _s (L ₁ ) ⋅ P _s (L ₂ ).

2. [1-2] Com probabilidade p _{dividida t, a} sentença gerada no idioma de destino se divide em duas sentenças não vazias, de modo que o número total de palavras aumenta exatamente uma. A probabilidade de uma sentença de comprimento L _t se dividir em partes do comprimento L1 e L2 (ou seja, L ₁ + L ₂ = L _t + 1) é proporcional a P _t (L ₁ ) ⋅ P _t (L ₂ ).

3. 3. [1-1] Com uma probabilidade de (1 - p _{dividir s} - p _{dividir t} ), nenhum dos pares de sentenças geradas decairá.

Solução

A tarefa é um caso especial de alinhamento usando modelos de Markov ocultos (alinhamento HMM). A idéia principal é que você possa calcular a probabilidade de gerar um par específico de documentos usando esse modelo e o algoritmo forward : nesse caso, o estado é um par de prefixos de documentos. Consequentemente, a probabilidade requerida de alinhamento de um par específico de sentenças paralelas pode ser calculada pelo algoritmo de avanço para trás .

D. Fita de recomendações

Condição

Considere um feed de recomendações para conteúdo heterogêneo. Ele mistura objetos de vários tipos (fotos, vídeos, notícias etc.). Esses objetos geralmente são ordenados por relevância para o usuário: quanto mais relevante (interessante) o objeto para o usuário, mais próximo ao topo da lista de recomendações. No entanto, com essa ordem, surgem frequentemente situações em que vários objetos do mesmo tipo aparecem na lista de recomendações. Isso piora bastante a variedade externa de nossas recomendações e, portanto, os usuários não gostam. É necessário implementar um algoritmo que, de acordo com a lista de recomendações, constitua uma nova lista que estará livre desse problema e será mais relevante.

Seja dada uma lista inicial de recomendações a = [a ₀ , a ₁ , ..., a _{n - 1} ] de comprimento n> 0. Um objeto com o número i possui um tipo com o número b _i ∈ {0, ..., m - 1}. Além disso, um objeto sob o número i tem relevância r (a _i ) = 2 _−i . Considere a lista que é obtida a partir da inicial escolhendo um subconjunto de objetos e reorganizando-os: x = [a _{i 0} , a _{i 1} , ..., a _{i k - 1} ] de comprimento k (0 ≤ k ≤ n). Uma lista é chamada admissível se não houver dois objetos consecutivos coincidentes no tipo, ou seja, b _{i j} ≠ b _{i j + 1} para todos os j = 0, ..., k - 2. A relevância da lista é calculada pela fórmula $$$\ sum_ {j = 0} ^ {k-1} 2 _ {- j} r (a_ {i_j})$. Você precisa encontrar a lista de relevância máxima entre todas as válidas.

Solução

Usando cálculos matemáticos simples, pode ser demonstrado que o problema pode ser resolvido por uma abordagem “gananciosa”, ou seja, na lista ideal de recomendações, cada item tem o objeto mais relevante de todos os que são válidos no mesmo início da lista. A implementação dessa abordagem é simples: pegamos objetos em uma linha e os adicionamos à resposta, se possível. Quando um objeto inválido é encontrado (cujo tipo coincide com o tipo do anterior), o colocamos de lado em uma fila separada, da qual o inserimos na resposta o mais rápido possível. Observe que, a todo momento, todos os objetos nessa fila terão um tipo correspondente. No final, vários objetos podem permanecer na fila, eles não serão mais incluídos na resposta.

  std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; } 

D. Clusterização de seqüências de caracteres

Existe um alfabeto finito A = {a ₁ , a ₂ , ..., a _{K - 1} , a _K = S}, a _i ∈ {a, b, ..., z}, S é o fim da linha.

Considere o seguinte método para gerar seqüências aleatórias sobre o alfabeto A:

1. O primeiro caractere x ₁ é uma variável aleatória com a distribuição P (x ₁ = a _i ) = q _i (sabe-se que q _K = 0).
2. Cada caractere seguinte é gerado com base no anterior, de acordo com a distribuição condicional P (x _i = a _j || x _{i - 1} = a _l ) = p _jl .
3. Se x _i = S, a geração para e o resultado é x ₁ x ₂ ... x _{i - 1} .

O conjunto de linhas geradas a partir de uma mistura de dois modelos descritos com diferentes parâmetros é dado. É necessário que cada linha forneça o índice da cadeia da qual foi gerada.

Solução

O problema é resolvido usando o algoritmo EM : supõe-se que a amostra apresentada seja gerada a partir de uma mistura de duas cadeias de Markov cujos parâmetros são restaurados durante as iterações. Uma restrição de 80% das respostas corretas é feita para que a correção da solução não seja afetada por exemplos com alta probabilidade nas duas cadeias. Esses exemplos, portanto, quando restaurados adequadamente, podem ser atribuídos a uma cadeia incorreta em termos da resposta gerada.

 import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs] # probs fixed p0, A = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) q0, B = empty_row(n_tokens), empty_matrix(n_tokens, n_tokens) for prob, sample in zip(probs, samples): p0[sample[0]] += prob q0[sample[0]] += 1 - prob for t1, t2 in zip(sample[:-1], sample[1:]): A[t1][t2] += prob B[t1][t2] += 1 - prob A, p0 = normalized_matrix(A), normalized_row(p0) B, q0 = normalized_matrix(B), normalized_row(q0) trans_log_diff = [ [math.log(b + EPS) - math.log(a + EPS) for b, a in zip(B_r, A_r)] for B_r, A_r in zip(B, A) ] # A, p0, B, q0 fixed probs = empty_row(n_samples) for i, sample in enumerate(samples): value = math.log(q0[sample[0]] + EPS) - math.log(p0[sample[0]] + EPS) for t1, t2 in zip(sample[:-1], sample[1:]): value += trans_log_diff[t1][t2] probs[i] = 1.0 / (1.0 + math.exp(value)) if max(abs(x - y) for x, y in zip(probs, old_probs)) < 1e-9: break return [int(x > 0.5) for x in probs] def main(): N, K = list(map(int, input().split())) string_samples = [] alphabet = list(input().strip()) + [''] for _ in range(N): string_samples.append(input().rstrip()) result = restore_params(alphabet, string_samples) for r in result: print(r) if __name__ == '__main__': main() 

---

.