O algoritmo de colapso da função de onda ensina um computador a improvisar. Na entrada, ele recebe dados arquetípicos e cria dados gerados proceduralmente semelhantes ao original.
( Fonte )Geralmente é usado para criar imagens, mas também pode construir
cidades ,
parques de skate e escrever
poemas terríveis .
( Fonte )O colapso da função de onda é um algoritmo de mente muito independente que praticamente não requer ajuda ou instruções externas. Você só precisa de um exemplo do estilo que deseja alcançar, e ele fará o resto. Apesar de sua auto-suficiência, ele é surpreendentemente simples. Ele não usa redes neurais, florestas aleatórias ou qualquer outra coisa que se assemelhe ao aprendizado de máquina. Se você lidar com a ideia, ela se tornará muito compreensível e intuitiva para você.
A maioria das implementações e explicações sobre o colapso da função de onda é uma versão completa e com otimização de velocidade do algoritmo. Obviamente, todos eles são importantes e necessários, mas é difícil entendê-los do zero. Neste post, explicarei tudo em uma linguagem simples que eu entendo, com foco na versão limitada do Wavefunction, que chamei de modelo
ainda mais simples . Além disso, publiquei
um exemplo de implementação do ESTM no Github . O código é ineficiente e lento, mas muito legível e comentado em detalhes. Assim que você entender a tecnologia subjacente ao ESTM, ficará mais perto de entender as versões mais complexas do algoritmo. Se você deseja entender o algoritmo de recolhimento da função de onda, este artigo será um bom começo.
Vamos começar com a história.
O casamento
Imagine que você está planejando seu casamento. Além da seleção de jóias e música, você precisa criar um plano de assentos para os convidados para o jantar. Sua família gosta de discutir e ser travessa, por isso pode ser difícil. Um pai não pode sentar-se a menos de duas mesas da mãe. Um primo fica solitário se não se senta com outro primo. E é melhor não plantar o tio Roy ao lado dos membros que respeitam o meio ambiente da família de seu parceiro. Restam apenas 5 horas antes da chegada dos alimentos, então você decide atacar essa tarefa teimosa usando o algoritmo de colapso da função de onda.
Você começa com uma longa lista de regras e um plano de assentos vazio.
Você cria a
função de onda original
do plano. Ela amarra cada cadeira a uma lista de pessoas que podem se sentar nela. Enquanto qualquer pessoa pode sentar em qualquer cadeira. A função de onda dos convidados começa com uma
superposição completa (o conceito é emprestado da física quântica) de cada esquema possível.
O gato de Schrödinger estava morto e vivo ao mesmo tempo até que alguém abriu a caixa e verificou; seu plano é ao mesmo tempo todo esquema possível até você colocar as coisas em ordem. Uma superposição completa é uma construção teórica útil, mas não ajudará sua avó a descobrir onde ela precisa se sentar. Você precisa trazer a função de onda da localização dos convidados para um determinado estado, que pode ser transformado em cartões de nome comuns, não quânticos.
Começamos a fazer isso executando o
colapso da função de onda para uma cadeira. Selecionamos uma cadeira, examinamos a lista de pessoas que podem sentar nela e a designamos aleatoriamente a uma delas. Nesse caso, a função de onda das fezes diminui.
Essa escolha tem consequências que se estendem às funções de onda das cadeiras restantes. Se o tio Roy estiver sentado na mesa 2, então a prima Frank e Michelle Obama (uma amiga da família do seu parceiro) definitivamente não estarão com ele. E se Michelle não se sentar na mesa 2, Barack também não estará atrás dele. Estamos atualizando a função de onda do plano de localização, excluindo pessoas das listas de possíveis candidatos.
Assim que as vibrações são estabilizadas, repetimos esse processo. Selecionamos outra cadeira com vários possíveis candidatos e reduzimos sua função de onda, escolhendo aleatoriamente uma das pessoas aceitáveis por ela. Novamente, estendemos as vibrações causadas por essa escolha para o restante do plano, removendo as pessoas da função de onda da cadeira, se elas não puderem mais se sentar nela.
Repetimos esse processo até a função de onda entrar em colapso (ou seja, exatamente uma pessoa sentada permanece nela) ou até chegarmos a uma
contradição . Contradição é uma cadeira em que ninguém pode sentar, porque todos foram expulsos devido a eleições anteriores. A contradição torna impossível o colapso de toda a função de onda.
Se você chegou a uma contradição, a maneira mais fácil é recomeçar. Descarte todo o trabalho anterior, encontre um novo plano vazio e inicie o algoritmo novamente, concluindo o colapso da função de onda para outra cadeira aleatória. Você também pode implementar um sistema de retorno que permita cancelar uma opção específica, em vez de abandonar tudo imediatamente ("e se Sheila for transferida para a cadeira 54?").
Depois de algumas falsas partidas, você finalmente alcançará um estado completamente colapsado no qual cada cadeira é designada para exatamente uma pessoa e todas as regras são seguidas. Feito!
Do casamento aos bitmaps
Este não é um exemplo teórico. Você pode realmente perceber uma variante do colapso da função de onda, que criará um plano de assentos para os convidados do casamento. No entanto, no colapso da função de onda mais tradicional, geralmente tentamos não acomodar as pessoas no casamento, mas organizar os pixels na imagem de saída. No entanto, o processo será muito semelhante. Ensinamos ao algoritmo um conjunto de regras que a saída deve satisfazer. Inicializamos a função de onda. Realizamos o colapso de um elemento e estendemos as conseqüências para o restante da função de onda. E continuamos a fazê-lo, até a função de onda entrar em colapso completamente ou até chegarmos a uma contradição.
O colapso tradicional da função de onda difere do colapso do casamento na maneira como ensinamos ao algoritmo as regras que ele deve seguir. Na versão do casamento, tivemos que escrever as regras. Mas na versão tradicional, apenas damos ao algoritmo uma imagem de exemplo e, com base nela, o algoritmo cria o restante. Ele analisa um exemplo, analisa seus padrões e descobre como pixels ou
blocos devem se alinhar.
Vamos começar a pesquisar o colapso real de uma função de onda observando um caso especial simples, que
ExUtumno (o criador do algoritmo) chama de
Modelo Simples em ExUtumno .
Modelo simples de azulejos
No Modelo de ladrilho simples, as imagens de entrada e saída são construídas a partir de um pequeno número de ladrilhos predefinidos, e cada quadrado na imagem de saída é limitado a apenas seus quatro vizinhos mais próximos. Por exemplo, suponha que geremos mundos aleatórios para um jogo bidimensional com uma vista superior. Podemos ter ladrilhos para terra, costa e mar, além de um conjunto de regras como "a costa pode estar perto do mar", "a terra pode estar perto da costa" e "o mar pode estar próximo a outro mar".
O modelo simples de ladrilhos leva em consideração a simetria e a rotação de seus ladrilhos. Por exemplo, as terras podem estar próximas à costa, mas apenas na orientação correta.
Esse processamento de simetria fornece melhores imagens de saída, mas complica o código. Para simplificar, vejamos uma visão ainda mais simples do colapso da função de onda, que eu chamei de
Modelo em mosaico ainda mais simples .
Modelo em mosaico ainda mais simples
Mesmo o modelo de ladrilhos mais simples ("um modelo de ladrilhos ainda mais simples") é semelhante ao modelo de ladrilhos simples, mas seus ladrilhos não têm propriedades de simetria. Cada bloco é um pixel da mesma cor, ou seja, não poderemos confundir suas arestas de forma alguma.
Regras de modelo em mosaico ainda mais simples determinam quais blocos podem ser colocados próximos um do outro e em qual orientação. Cada regra é uma tupla de três elementos (três tuplas): dois blocos e uma direção. Por exemplo,
(SEA, COAST, LEFT) significa que o ladrilho
SEA (mar) pode ser
partir do ladrilho
COAST (costa). Esta regra deve ser acompanhada por outra regra que descreva a situação em termos de
COAST -
(COAST, SEA, RIGHT) .
Se você deseja que os ladrilhos
SEA estejam localizados não apenas à
, mas também à
dos ladrilhos
COAST . então eles precisam de regras adicionais:
(SEA, COAST, RIGHT) e
(COAST, SEA, LEFT) .
Como eu disse acima, não precisamos criar uma lista de todas essas regras. O recolhimento da função de onda pode criar um conjunto de regras para o Modelo de mosaico ainda mais simples, analisando uma imagem de exemplo e coletando uma lista de todas as três tuplas que ela contém.
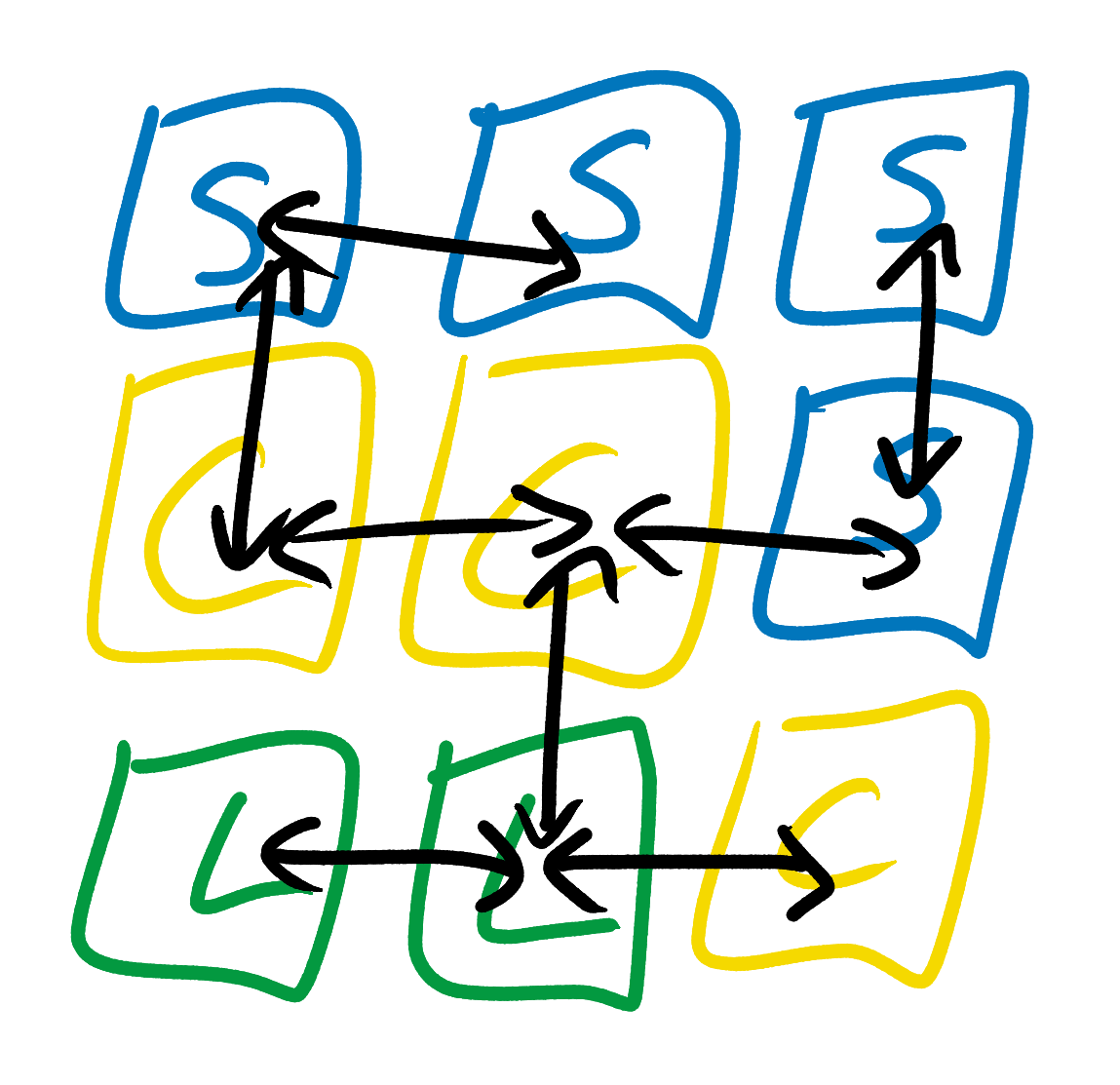
Tendo examinado a imagem de exemplo mostrada acima, o Modelo de mosaico ainda mais simples percebe que os ladrilhos do mar só podem estar embaixo ou ao lado dos ladrilhos da costa ou em qualquer lugar próximo a outros ladrilhos do mar. Ela também observa que os ladrilhos costeiros podem ser localizados ao lado de terra, mar ou outros ladrilhos costeiros, mas apenas acima dos ladrilhos marítimos e sob os ladrilhos terrestres. Ela não tenta derivar regras mais complexas, por exemplo, "azulejos do mar devem estar perto de pelo menos um azulejo do mar" ou "cada ilha deve conter pelo menos um azulejo do mar". Nenhum dos blocos pode afetar o fato de que alguns tipos de blocos podem ou não podem ser localizados a dois ou mais quadrados deles. É semelhante a um modelo de plano de casamento no qual a única regra é: "X pode sentar-se ao lado de Y".
Ao analisar a imagem recebida, também precisamos registrar a frequência com que cada uma das peças se encontra. Posteriormente, usamos esses números como pesos ao escolher a função de onda do quadrado, cujo recolhimento deve ser executado e também ao escolher o bloco atribuído ao quadrado quando ele é recolhido.
Tendo aprendido as regras às quais a imagem de saída deve aderir, estamos prontos para criar o colapso da função de onda da imagem de saída.
Reduzir
Como no exemplo do casamento, começamos o processo de recolhimento com uma função de onda na qual cada quadrado da imagem de saída está em uma superposição de cada tipo de bloco.
Começamos escolhendo um quadrado cuja função de onda entrará em colapso. No exemplo do casamento, essa escolha foi feita por acaso. No entanto, como
ExUtumno observou, as pessoas geralmente abordam essas tarefas de maneira diferente. Em vez disso, eles procuram quadrados com a menor
entropia . Entropia é uma medida de incerteza e desordem. Em geral, um quadrado com alta entropia é um quadrado com muitas peças possíveis restantes em sua função de onda. Ainda não está claro para qual peça ele finalmente desmorona. Um quadrado de baixa entropia é um quadrado com o menor número possível de peças na função de onda. O conjunto de peças, para um dos quais ele desmorona como resultado, já é muito limitado.
Por exemplo, no Modelo de mosaico ainda mais simples, um quadrado sem informações sobre os quadrados circundantes é ilimitado e pode se tornar qualquer mosaico. Portanto, tem uma entropia muito alta. Mas um quadrado em torno do qual vários quadrados já desabaram pode ter apenas 2 peças.
A função de onda do quadrado central na figura acima não entrou em colapso completamente, mas já sabemos que não pode ser um bloco de terra. No entanto, ele já é limitado, o que significa que tem uma
entropia inferior à do quadrado superior direito, que ainda pode ser terrestre, marítimo ou costeiro.
São peças tão limitadas e com baixa entropia que as pessoas geralmente prestam atenção quando resolvem esses problemas manualmente. Mesmo se você não usar o colapso da função de onda para criar um plano para colocar convidados no casamento e elaborá-lo por conta própria, concentre-se nas áreas do plano que já possuem o maior número de restrições. Você não colocará Dwayne na tabela 1 e depois saltará aleatoriamente para obter Katie na tabela 7 (que ainda está vazia). Primeiro você coloca Dwayne, depois descobre quem pode sentar ao lado dele, quem pode sentar ao lado dessa pessoa e assim por diante. Ainda não vi justificativa para isso, mas minha intuição diz que o uso dessa
heurística de entropia mínima provavelmente produzirá menos
contradições do que se você selecionar aleatoriamente quadrados para colapso.
A
fórmula de Shannon é usada como fórmula de entropia no algoritmo de colapso da função de onda. Ele usa os pesos dos blocos que analisamos da imagem recebida na etapa anterior:
# Sums are over the weights of each remaining # allowed tile type for the square whose # entropy we are calculating. shannon_entropy_for_square = log(sum(weight)) - (sum(weight * log(weight)) / sum(weight))
Tendo calculado o quadrado da função de onda com a menor entropia, reduzimos sua função de onda. Fazemos isso escolhendo aleatoriamente um dos ladrilhos que ainda estão disponíveis para o quadrado, ponderado pelo peso dos ladrilhos que analisamos da imagem recebida. Os pesos são usados porque fornecem uma imagem de saída mais realista. Suponha que a função de onda de um quadrado relate que pode ser terra ou costa. Nem sempre temos que escolher uma das opções com probabilidade de 50%. Se a imagem de entrada tiver mais blocos de terra do que a costa, devemos refletir essa vantagem na imagem de saída. Isso é realizado usando pesos globais simples. Se na imagem de exemplo houver
20 mosaicos terrestres e
10 costeiros, o quadrado entrará em colapso com uma probabilidade de
2/3 e no litoral com uma probabilidade restante de
1/3 .
Em seguida, estendemos as conseqüências da escolha para o restante da função de onda da saída ("se esse ladrilho acabou sendo o mar, esse ladrilho não pode ser terra, ou seja, não pode ser a costa"). Quando todos esses tremores se estabilizarem, repetimos o processo usando a heurística de entropia mínima para selecionar o próximo bloco em colapso. Repetimos esse ciclo de colapso-propagação, até que toda a função de onda da imagem de saída colapse completamente e possamos retornar o resultado, ou até chegarmos a uma contradição e retornarmos um erro.
Como resultado, criamos um mundo (ou erro).
Para onde ir a seguir
Depois de lidar com o modelo de mosaico ainda mais simples, você está pronto para subir a escada de poder e complexidade do algoritmo. Comece com o Modelo lado a lado simples que mencionamos no início deste post e depois vá para o Modelo de sobreposição completo. No modelo sobreposto, blocos ou pixels afetam-se à distância. Se você entender essas coisas, o
ExUtumno perceberá que o Simple Tiled Model é semelhante à cadeia de Markov da ordem 1, e os modelos mais complexos se assemelham a cadeias de uma ordem maior.
O colapso da função de onda pode até levar em conta restrições adicionais, por exemplo, "esse bloco deve ser marítimo" ou "este pixel deve ser vermelho" ou "pode haver apenas um monstro na saída". Tudo isso é descrito no
README do projeto principal . Você também pode estudar as otimizações de velocidade feitas para a implementação completa. Não é necessário recalcular a entropia de cada quadrado em cada iteração, e a disseminação de informações pela função de onda pode ser feita muito mais rapidamente. Esses aspectos se tornam mais importantes à medida que o tamanho das imagens de saída aumenta.
O colapso da função de onda é uma ferramenta bonita e poderosa que vale a pena dominar. Pense nisso na próxima vez que planejar um casamento ou gerar um mundo processual.