A segmentação manual do pulmão leva cerca de 10 minutos e requer uma certa habilidade para obter o mesmo resultado de alta qualidade que a segmentação automática. A segmentação automática leva cerca de 15 segundos.
Supus que, sem uma rede neural, seria possível obter uma precisão de não mais que 70%. Eu também assumi que operações morfológicas são apenas a preparação de uma imagem para algoritmos mais complexos. Mas, como resultado do processamento dessas, embora poucas, 40 amostras de dados tomográficos disponíveis, o algoritmo segmentou os pulmões sem erros. Além disso, após o teste nos cinco primeiros casos, o algoritmo não mudou significativamente e funcionou corretamente nos outros 35 estudos sem alterar as configurações.
Além disso, as redes neurais têm uma desvantagem - para seu treinamento, precisamos de centenas de amostras de pulmão, que precisam ser marcadas manualmente.
Conteúdo
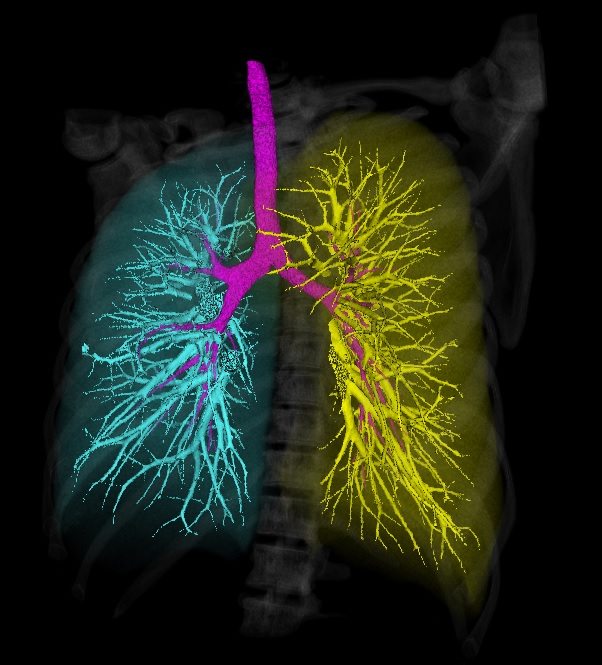
Estrutura do sistema respiratório
O sistema respiratório inclui as vias aéreas e os pulmões. As vias aéreas são divididas nas vias aéreas superior e inferior. O ponto de separação entre o trato respiratório inferior e superior é o ponto de intersecção do esôfago com as vias aéreas. Todos os órgãos que estão acima da laringe são o trato superior e a laringe e os órgãos abaixo são o trato inferior.
Lista dos órgãos respiratórios:
A cavidade nasal é uma cavidade cheia de ar entre o nariz e a faringe.
A faringe é um canal através do qual a comida e o ar viajam.
A traquéia é um tubo conectado à laringe e brônquios.
A laringe é responsável pela formação da voz. Está no nível das vértebras cervicais C4-C6.
Os brônquios são os canais respiratórios, cuja parte principal está localizada dentro dos pulmões.
Os pulmões são o principal órgão respiratório.

Escala de Haunsfield
Godfrey Hounsfield era um engenheiro elétrico inglês que, juntamente com o teórico americano Allan Cormack, desenvolveu tomografia computadorizada, pela qual compartilhou o Prêmio Nobel em 1979.

A escala de Hounsfield - é uma escala quantitativa para descrever a radiodensidade, medida em unidades de Hounsfield, denominada HU.
A radiodensidade é calculada com base no coeficiente de atenuação da radiação. O coeficiente de atenuação caracteriza a facilidade com que um volume de material pode ser penetrado pela radiação.
A radiodensidade é calculada pela fórmula:
$$ display $$ {μ_ {X} -μ_ {water} \ over μ_ {water} -μ_ {air}} \ times 1000 $$ display $$
onde são coeficientes de atenuação linear para o material medido, água e ar.
A radiodensidade pode ser negativa porque a radiodensidade zero corresponde à água. Isso significa que todos os materiais com um coeficiente de atenuação menor que o coeficiente de atenuação da água (por exemplo, tecido pulmonar, ar) terão uma radiodensidade negativa.
As radiodensidades aproximadas para vários tecidos estão listadas abaixo:
- Ar: -1000 HU.
- Órgãos respiratórios: de -950 a -300 HU.
- Sangue (sem contrastar os vasos): de 0 a 100 HU.
- Ossos: 100 a 1000 HU.

Links para a Wikipedia: escala de Hounsfield , Godfrey Hounsfield , coeficiente de atenuação .
Morfologia matemática
As operações morfológicas são as principais ferramentas utilizadas no algoritmo.
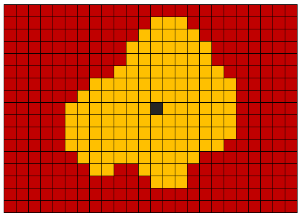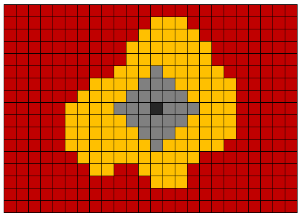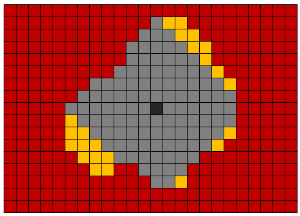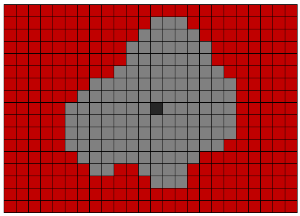
No campo da visão computacional, as operações morfológicas são chamadas de grupo de algoritmos para a transformação da forma dos objetos. Na maioria das vezes, operações morfológicas são aplicadas a imagens binarizadas, onde as unidades correspondem a voxels de objetos e os zeros a vazios.
As principais operações morfológicas incluem:
Dilatação morfológica é a adição de novos voxels a todos os voxels de borda dos objetos. Em outras palavras, o algoritmo verifica todos os voxels correspondentes à borda do objeto e os amplia usando um kernel com uma determinada forma (esfera, cubo, cruz etc). O núcleo tem seu próprio raio (para a esfera) ou a largura do lado (para o cubo). Essa operação é frequentemente usada para mesclar vários objetos próximos em um único objeto.
A erosão morfológica é o corte de todos os voxels situados na borda (limite) dos objetos. Esta operação é inversa à dilatação. Esta operação é útil para remover ruídos que têm a forma de muitos pequenos objetos interconectados. No entanto, esse método de remoção de ruído deve ser usado apenas se o objeto de interesse tiver uma espessura muito maior que o raio de erosão. Caso contrário, as informações úteis serão perdidas.
O fechamento morfológico é uma dilatação seguida por uma erosão. É usado para fechar furos dentro de objetos e mesclar objetos próximos.
A abertura morfológica é uma erosão seguida de uma dilatação. É usado para remover pequenos objetos com ruído e separá-los em vários objetos.

Algoritmo de Lee e compactação RLE
Para selecionar objetos no volume binário de voxel, o algoritmo de Lie é usado. Originalmente, esse algoritmo foi inventado para encontrar a saída mais curta do labirinto. Nós o usamos para selecionar o objeto e movê-lo de uma matriz tridimensional de voxels para outra. A idéia básica do algoritmo consiste em movimento paralelo em todas as direções possíveis a partir do ponto de partida. Para um caso tridimensional, é possível mover-se em 26 ou 6 direções a partir de um voxel.
Para otimizar o desempenho, o algoritmo de codificação de execução foi aplicado. A idéia principal do algoritmo é que a sequência de uns e zeros seja substituída por um dígito igual ao número de elementos na sequência. Por exemplo, a cadeia "00110111" pode ser substituída por: "2; 2; 1; 3 ". Isso reduz o número de acessos à memória.

Links da Wikipedia: algoritmo de Lee , algoritmo RLE .
Transformação de limiar do volume base
Utilizando o tomógrafo, foram obtidos os dados sobre uma radiodensidade em cada ponto do espaço digitalizado. Os voxels do ar têm uma radiodensidade na faixa de -1100 a -900 HU, e os voxels dos órgãos respiratórios têm uma radiodensidade de -900 a -300 HU. Portanto, podemos remover todos os voxels desnecessários com radiodensidade maior que -300 HU. Como resultado, obtemos um volume de voxel binarizado contendo apenas os órgãos respiratórios e o ar.
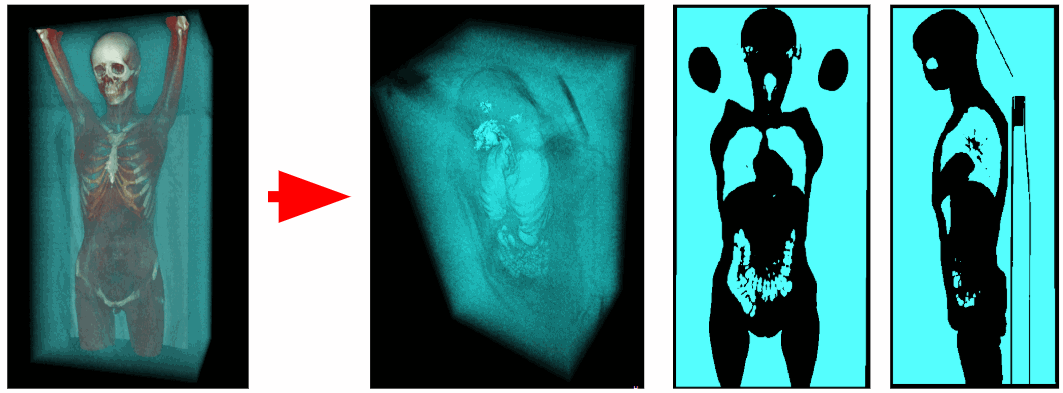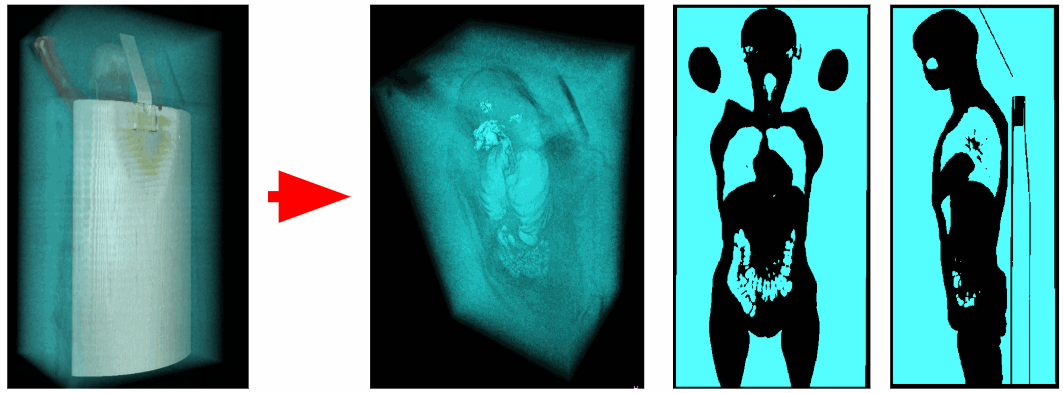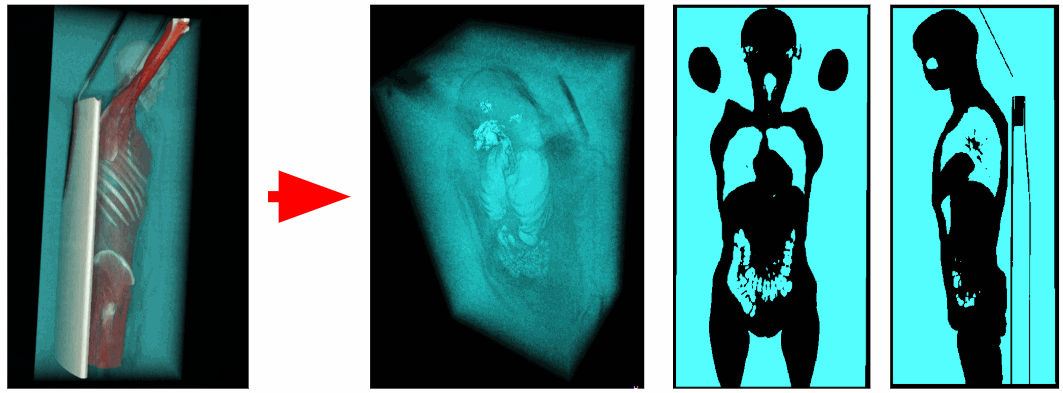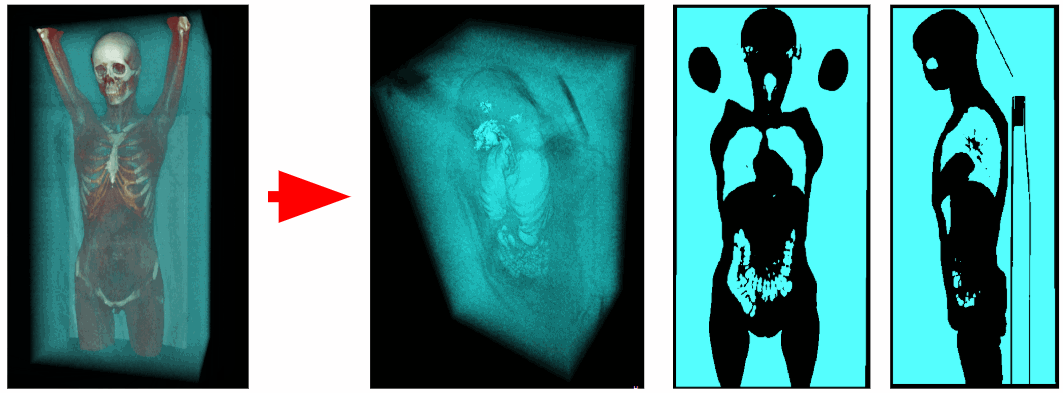
Remoção de ar externo
Para segmentar o ar interno do corpo, excluímos todos os objetos adjacentes aos cantos do volume 3D. Assim, removemos o ar externo.

No entanto, nem em todos os casos o ar dentro da mesa do tomógrafo será removido, pois pode não haver conexão com os cantos do volume 3D.

Portanto, analisaremos não apenas os cantos, mas também todos os voxels localizados em qualquer um dos planos de arestas do f. Mas, como podemos ver na imagem abaixo, os pulmões também foram removidos. Acontece que a traquéia também teve uma conexão com o plano superior do volume 3D.
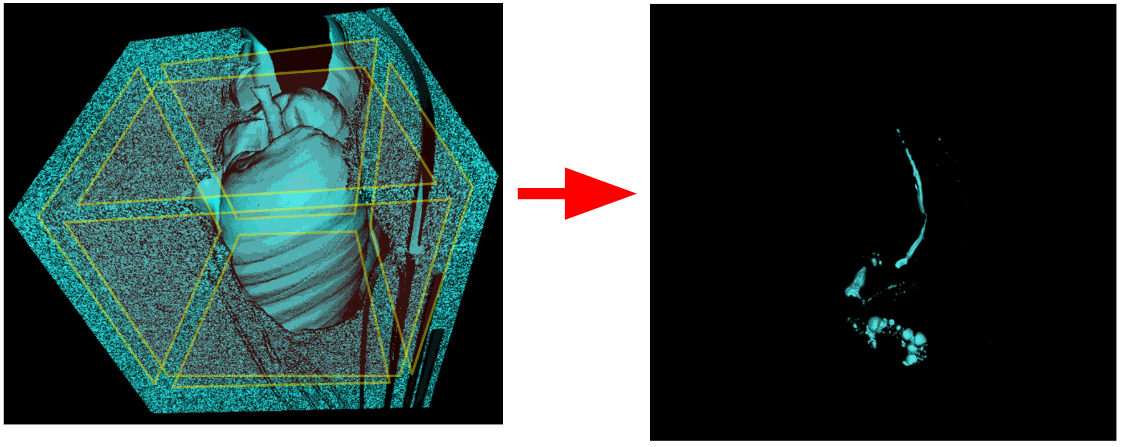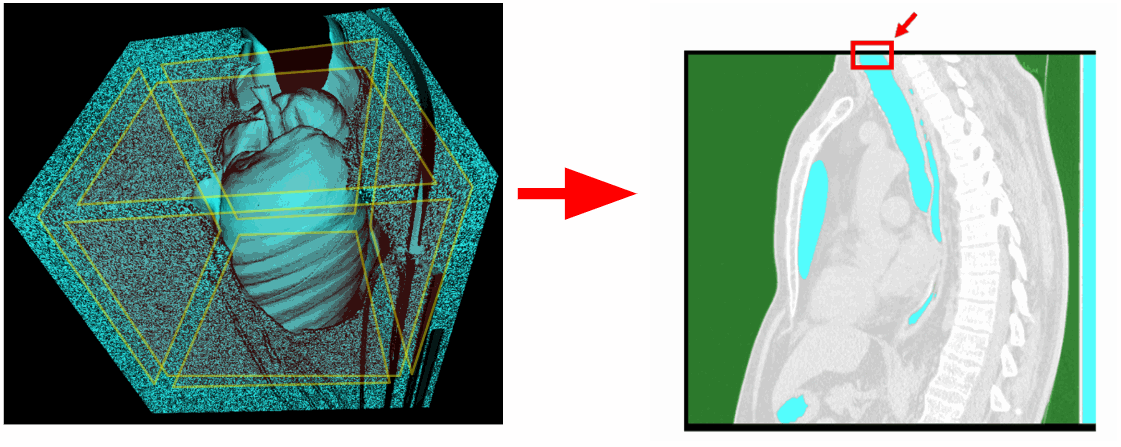
Teremos que excluir o plano superior da área de digitalização. Também existem estudos em que os pulmões não foram totalmente capturados e o plano inferior está conectado aos pulmões.
Portanto, se desejar, você também pode excluir o plano inferior.

Mas esse método afeta apenas estudos no peito. No caso da captura de todo o volume do corpo, a conexão do ar interno e externo através da cavidade nasal aparecerá. Portanto, é necessário aplicar erosão morfológica para separar o ar interno e externo.
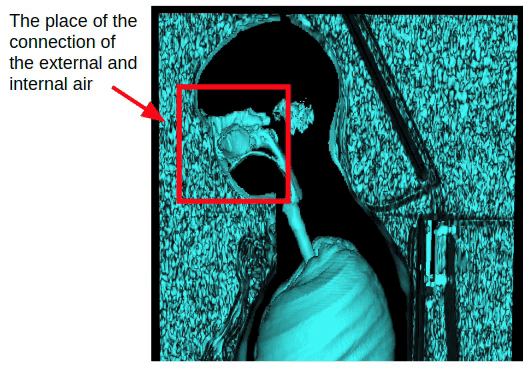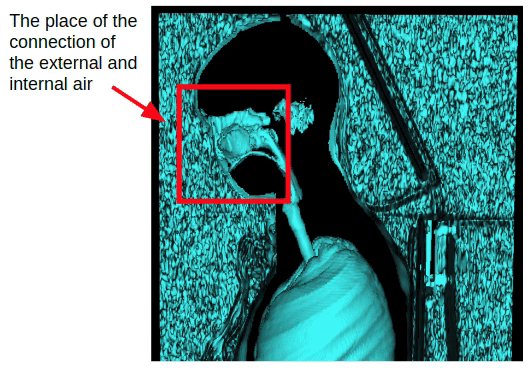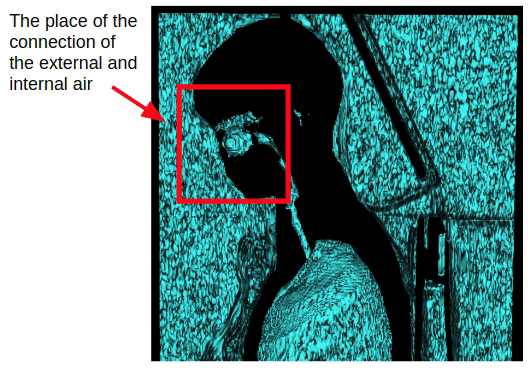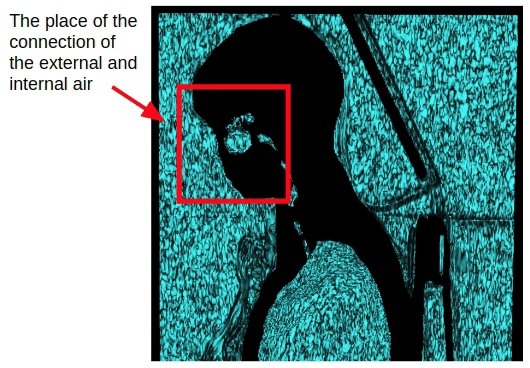
Após a aplicação da erosão, podemos retornar ao método de segmentação do ar externo obtido anteriormente, que se baseia na conectividade do ar externo com planos laterais do volume 3D.

Após a segmentação do ar externo, poderíamos subtrair imediatamente o ar externo de todo o volume do ar e dos pulmões e obter o ar interno do corpo e dos pulmões. Mas há um problema. Após a erosão, algumas informações sobre o ar externo foram perdidas. Para restaurá-lo, aplicamos dilatação do ar externo.

Em seguida, subtraímos o ar externo de todo o ar e órgãos respiratórios e obtemos o ar interno e os órgãos respiratórios.


Segmentação do objeto de volume máximo
A seguir, segmentamos os órgãos respiratórios como o objeto máximo em volume. Os órgãos respiratórios não têm conexão com o ar no interior do trato gastrointestinal.


Vale ressaltar que a escolha correta do limiar de radiodensidade na etapa inicial é importante. Caso contrário, em alguns casos, pode não haver conexão entre os dois pulmões como resultado de baixa resolução. Por exemplo, se assumirmos que os voxels dos órgãos respiratórios têm radiodensidade de -500 HU e menos, no caso abaixo, a segmentação dos órgãos respiratórios como o maior objeto em volume levará a um erro, porque não há conexão entre os dois pulmões. Portanto, o limite deve ser aumentado para -300 HU.

Fechando os vasos dentro dos pulmões
Para capturar os vasos dentro dos pulmões, usaremos fechamento morfológico, ou seja, dilatação seguida de erosão com o mesmo raio. A radiodensidade dos vasos (sem contraste) é de cerca de 0..100 HU.

Na imagem, podemos ver que grandes canais sanguíneos não estão fechados. Mas isso não é necessário. O objetivo desta operação era destruir os muitos pequenos orifícios dentro dos pulmões para simplificar o processo de segmentação pulmonar nas próximas etapas.
Algoritmo de segmentação de órgãos respiratórios
Como resultado, obtemos o seguinte algoritmo de segmentação de órgãos respiratórios:
- Transformação de limite do volume base com o limite "<-300 HU".
- Erosão morfológica com raio de 3 mm para a separação do ar externo e interno.
- Segmentação do ar externo com base na conectividade do ar externo com os planos laterais de limite do volume 3D.
- Dilatação morfológica do ar externo para restaurar as informações perdidas após a erosão.
- Subtração do ar externo de todo o ar e órgãos respiratórios para obter o ar interno e os órgãos respiratórios.
- Segmentação do objeto de volume máximo.
- Fechamento morfológico dos vasos dentro dos pulmões.

Implementação de algoritmos no MATLAB
Função "getRespiratoryOrgans"
Função "getExternalAir"
Função "getMaxObject"
O código fonte pode ser baixado pela referência .
Conclusão
Os seguintes artigos serão:
- segmentação de traquéia e brônquios;
- segmentação pulmonar;
- segmentação dos lobos pulmonares.
Os seguintes algoritmos serão considerados:
- transformação à distância;
- transformação de vizinho mais próximo, também conhecida como transformação de recurso;
- cálculo dos autovalores da matriz de Hessian para segmentação de objetos 3D planos;
- segmentação de bacias hidrográficas.