Redes neurais e aprendizado profundo, capítulo 4: Prova visual de que as redes neurais podem calcular qualquer função

Neste capítulo, dou uma explicação simples e principalmente visual do teorema da universalidade. Para seguir o material deste capítulo, você não precisa ler os anteriores. Está estruturado como um ensaio independente. Se você possui o entendimento mais básico do NS, deve poder entender as explicações.


Um dos fatos mais surpreendentes sobre as redes neurais é que elas podem calcular qualquer função. Ou seja, digamos que alguém lhe dê algum tipo de função complexa e sinuosa f (x):



E, independentemente dessa função, é garantida uma rede neural que, para qualquer entrada x, o valor f (x) (ou alguma aproximação próxima a ela) será a saída dessa rede, ou seja:



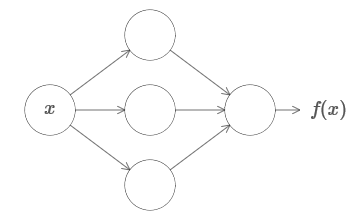
Isso funciona mesmo que seja uma função de muitas variáveis ​​f = f (x ₁ , ..., x _m ) e com muitos valores. Por exemplo, aqui está uma rede que calcula uma função com m = 3 entradas en = 2 saídas:



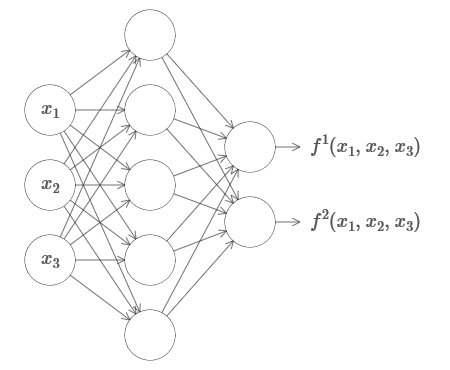
Esse resultado sugere que as redes neurais têm uma certa universalidade. Independentemente da função que queremos calcular, sabemos que existe uma rede neural que pode fazer isso.

Além disso, o teorema da universalidade se mantém mesmo se restringirmos a rede a uma única camada entre os neurônios de entrada e saída - os chamados em uma camada oculta. Assim, mesmo redes com uma arquitetura muito simples podem ser extremamente poderosas.

O teorema da universalidade é bem conhecido pelas pessoas que usam redes neurais. Mas, embora seja assim, uma compreensão desse fato não é tão difundida. E a maioria das explicações para isso é tecnicamente complexa demais. Por exemplo, um dos primeiros trabalhos que comprova esse resultado usou o teorema de Hahn - Banach , o teorema de representação de Riesz e algumas análises de Fourier. Se você é matemático, é fácil entender essas evidências, mas para a maioria das pessoas não é tão fácil. É uma pena, porque as razões básicas da universalidade são simples e bonitas.

Neste capítulo, dou uma explicação simples e principalmente visual do teorema da universalidade. Vamos seguir passo a passo as idéias subjacentes. Você entenderá por que as redes neurais podem realmente calcular qualquer função. Você entenderá algumas das limitações deste resultado. E você entenderá como o resultado está associado ao NS profundo.

Para seguir o material deste capítulo, você não precisa ler os anteriores. Está estruturado como um ensaio independente. Se você possui o entendimento mais básico do NS, deve poder entender as explicações. Às vezes, porém, fornecerei links para material anterior para ajudar a preencher as lacunas de conhecimento.

Os teoremas da universalidade são freqüentemente encontrados na ciência da computação, então às vezes até esquecemos o quão incrível eles são. Mas vale lembrar: a capacidade de calcular qualquer função arbitrária é realmente incrível. Quase todo processo que você pode imaginar pode ser reduzido ao cálculo de uma função. Considere a tarefa de encontrar o nome de uma composição musical com base em uma breve passagem. Isso pode ser considerado um cálculo de função. Ou considere a tarefa de traduzir um texto chinês para o inglês. E isso pode ser considerado um cálculo de função (de fato, muitas funções, pois existem muitas opções aceitáveis ​​para traduzir um único texto). Ou considere a tarefa de gerar uma descrição do enredo do filme e a qualidade da atuação com base no arquivo mp4. Isso também pode ser considerado como o cálculo de uma determinada função (a observação feita sobre as opções de tradução de texto também está correta aqui). Universalidade significa que, em princípio, os NSs podem executar todas essas tarefas e muitas outras.

Obviamente, apenas pelo fato de sabermos que existem NSs capazes de, por exemplo, traduzir do chinês para o inglês, não se segue que temos boas técnicas para criar ou mesmo reconhecer uma rede desse tipo. Essa restrição também se aplica aos teoremas tradicionais da universalidade para modelos como esquemas booleanos. Mas, como já vimos neste livro, o NS possui algoritmos poderosos para funções de aprendizado. A combinação de algoritmos de aprendizagem e versatilidade é uma mistura atraente. Até agora, no livro, nos concentramos em algoritmos de treinamento. Neste capítulo, focaremos na versatilidade e no que isso significa.

Dois truques

Antes de explicar por que o teorema da universalidade é verdadeiro, quero mencionar dois truques contidos na declaração informal "uma rede neural pode calcular qualquer função".

Primeiro, isso não significa que a rede possa ser usada para calcular com precisão qualquer função. Só podemos obter uma aproximação tão boa quanto precisamos. Ao aumentar o número de neurônios ocultos, melhoramos a aproximação. Por exemplo, eu ilustrei anteriormente uma rede que computa uma determinada função f (x) usando três neurônios ocultos. Para a maioria das funções, usando três neurônios, apenas uma aproximação de baixa qualidade pode ser obtida. Ao aumentar o número de neurônios ocultos (digamos, até cinco), geralmente podemos obter uma aproximação melhorada:



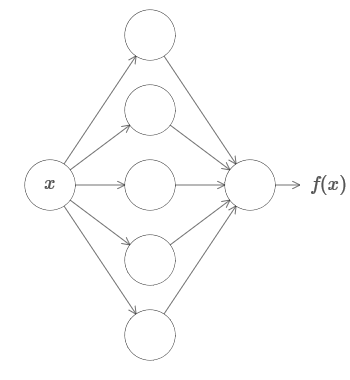
E para melhorar a situação aumentando ainda mais o número de neurônios ocultos.

Para esclarecer esta afirmação, digamos que recebemos uma função f (x), que queremos calcular com a precisão necessária ε> 0. Há uma garantia de que, ao usar um número suficiente de neurônios ocultos, sempre podemos encontrar um NS cuja saída g (x) satisfaça a equação | g (x) −f (x) | <ε para qualquer x. Em outras palavras, a aproximação será alcançada com a precisão desejada para qualquer valor de entrada possível.

O segundo problema é que as funções que podem ser aproximadas pelo método descrito pertencem a uma classe contínua. Se a função for interrompida, ou seja, ocorrer saltos bruscos repentinos, no caso geral, será impossível aproximar com a ajuda do NS. E isso não é surpreendente, já que nossos NSs calculam funções contínuas de dados de entrada. No entanto, mesmo que a função que realmente precisamos calcular seja descontínua, a aproximação geralmente é bastante contínua. Se sim, então podemos usar o NS. Na prática, essa limitação geralmente não é importante.

Como resultado, uma declaração mais precisa do teorema da universalidade será que NS com uma camada oculta pode ser usado para aproximar qualquer função contínua com a precisão desejada. Neste capítulo, provamos uma versão um pouco menos rigorosa desse teorema, usando duas camadas ocultas em vez de uma. Nas tarefas, descreverei brevemente como essa explicação pode ser adaptada, com pequenas alterações, a uma prova que usa apenas uma camada oculta.

Versatilidade com uma entrada e um valor de saída

Para entender por que o teorema da universalidade é verdadeiro, começamos entendendo como criar uma função de aproximação NS com apenas uma entrada e um valor de saída:



Acontece que essa é a essência da tarefa da universalidade. Depois que entendermos esse caso especial, será bastante fácil estendê-lo para funções com muitos valores de entrada e saída.

Para criar um entendimento de como construir uma rede para contar f, começamos com uma rede contendo uma única camada oculta com dois neurônios ocultos e com uma camada de saída contendo um neurônio de saída:



Para imaginar como os componentes de rede funcionam, nos concentramos no neurônio oculto superior. No diagrama do artigo original, você pode alterar interativamente o peso com o mouse, clicando em "w" e ver imediatamente como a função calculada pelo neurônio oculto superior muda:



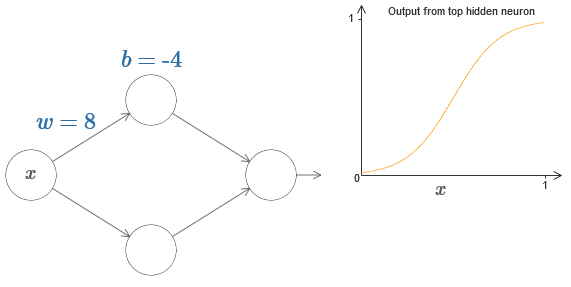
Como aprendemos anteriormente no livro, um neurônio oculto conta σ (wx + b), onde σ (z) ≡ 1 / (1 + e ^-z ) é um sigmóide . Até agora, usamos essa forma algébrica com bastante frequência. No entanto, para provar a universalidade, seria melhor ignorarmos completamente essa álgebra e, em vez disso, manipularmos e observarmos a forma no gráfico. Isso não apenas o ajudará a sentir melhor o que está acontecendo, mas também nos fornecerá uma prova de universalidade aplicável a outras funções de ativação além do sigmóide.

A rigor, a abordagem visual que escolhi não é tradicionalmente considerada evidência. Mas acredito que a abordagem visual fornece mais informações sobre a verdade do resultado final do que as provas tradicionais. E, é claro, esse entendimento é o real objetivo da prova. Nas evidências que proponho, as lacunas ocasionalmente aparecerão; Darei evidências visuais razoáveis, mas nem sempre rigorosas. Se isso o incomoda, considere sua tarefa preencher essas lacunas. No entanto, não perca de vista o objetivo principal: entender por que o teorema da universalidade é verdadeiro.

Para começar com essa prova, clique no deslocamento b no diagrama original e arraste para a direita para aumentá-lo. Você verá que, com um aumento no deslocamento, o gráfico se move para a esquerda, mas não muda de forma.

Em seguida, arraste-o para a esquerda para reduzir o deslocamento. Você verá que o gráfico está se movendo para a direita sem alterar a forma.

Reduza o peso para 2-3. Você verá que, à medida que o peso diminui, a curva se endireita. Para que a curva não fuja do gráfico, talvez seja necessário corrigir o deslocamento.

Por fim, aumente o peso para valores maiores que 100. A curva se tornará mais íngreme e, eventualmente, se aproximará da etapa. Tente ajustar o deslocamento para que seu ângulo fique na região do ponto x = 0,3. O vídeo abaixo mostra o que deve acontecer:



Podemos simplificar bastante nossa análise aumentando o peso, para que o resultado seja realmente uma boa aproximação da função step. Abaixo, construí a saída do neurônio oculto superior para o peso w = 999. Esta é uma imagem estática:



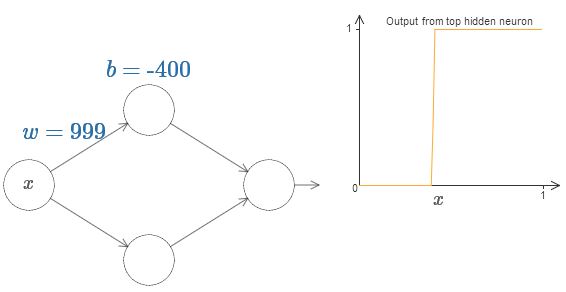
Usar funções de passo é um pouco mais fácil do que com o sigmóide típico. A razão é que as contribuições de todos os neurônios ocultos são adicionadas na camada de saída. A soma de várias funções de etapa é fácil de analisar, mas é mais difícil falar sobre o que acontece quando várias curvas são adicionadas na forma de um sigmóide. Portanto, será muito mais simples supor que nossos neurônios ocultos produzam funções graduais. Mais precisamente, fazemos isso fixando o peso w em um valor muito grande e atribuindo a posição da etapa através do deslocamento. Obviamente, trabalhar com uma saída como uma função step é uma aproximação, mas é muito bom, e até agora trataremos a função como uma verdadeira função step. Mais tarde, voltarei a discutir o efeito dos desvios dessa aproximação.

Qual o valor de x é o passo? Em outras palavras, como a posição do degrau depende do peso e do deslocamento?

Para responder à pergunta, tente alterar o peso e o deslocamento no gráfico interativo. Você consegue entender como a posição do passo depende de eb? Ao praticar um pouco, você pode se convencer de que sua posição é proporcional a be inversamente proporcional a w.

De fato, o passo é s = −b / w, como será visto se ajustarmos o peso e o deslocamento com os seguintes valores:



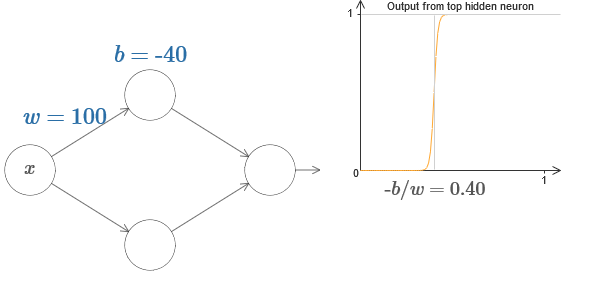
Nossas vidas serão bastante simplificadas se descrevermos os neurônios ocultos com um único parâmetro, s, isto é, pela posição do passo, s = −b / w. No diagrama interativo a seguir, você pode simplesmente alterar s:



Como observado acima, atribuímos um peso w na entrada a um valor muito grande - suficientemente grande para que a função step se torne uma boa aproximação. E podemos facilmente transformar o neurônio parametrizado dessa maneira de volta à sua forma usual, escolhendo o viés b = -ws.

Até agora, concentramo-nos apenas na produção do neurônio oculto superior. Vejamos o comportamento de toda a rede. Suponha que os neurônios ocultos calculem as funções do passo definidas pelos parâmetros dos passos s ₁ (neurônio superior) es ₂ (neurônio inferior). Seus respectivos pesos de saída são w ₁ e w ₂ . Aqui está a nossa rede:



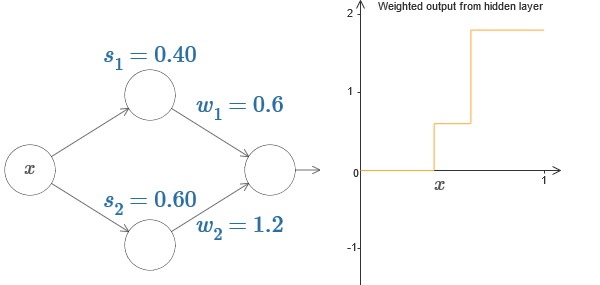
À direita, está um gráfico da saída ponderada w ₁ a ₁ + w ₂ a _{2 da} camada oculta. Aqui ₁ e ₂ são as saídas dos neurônios ocultos superior e inferior, respectivamente. Eles são indicados por "a", como costumam ser chamados de ativações neuronais.

A propósito, notamos que a saída de toda a rede é σ (w ₁ a ₁ + w ₂ a ₂ + b), onde b é o viés do neurônio de saída. Obviamente, isso não é o mesmo que a saída ponderada da camada oculta, cujo gráfico estamos construindo. Mas, por enquanto, vamos nos concentrar na saída equilibrada da camada oculta e só mais tarde pensar em como ela se relaciona com a saída de toda a rede.

Tente aumentar e diminuir a etapa _{1 do} neurônio oculto superior no diagrama interativo no artigo original . Veja como isso altera a saída ponderada da camada oculta. É especialmente útil entender o que acontece quando s ₁ excede s ₂ . Você verá que o gráfico nesses casos muda de forma, à medida que passamos de uma situação na qual o neurônio oculto superior é ativado primeiro para uma situação na qual o neurônio oculto inferior é ativado primeiro.

Da mesma forma, tente manipular a etapa s _{2 do} neurônio oculto inferior e veja como isso altera a produção geral dos neurônios ocultos.

Tente reduzir e aumentar os pesos de saída. Observe como isso aumenta a contribuição dos neurônios ocultos correspondentes. O que acontece se um dos pesos for igual a 0?

Por fim, tente definir w ₁ a 0,8 e w ₂ a -0,8. O resultado é uma função de “protrusão”, com início em s ₁ , final em s ₂ e altura de 0,8. Por exemplo, uma saída ponderada pode ser assim:



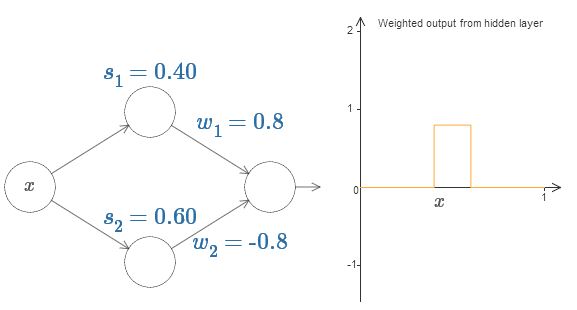
Obviamente, a protrusão pode ser dimensionada para qualquer altura. Vamos usar um parâmetro, h, denotando altura. Além disso, por simplicidade, vou me livrar da notação "s ₁ = ..." e "w ₁ = ...".



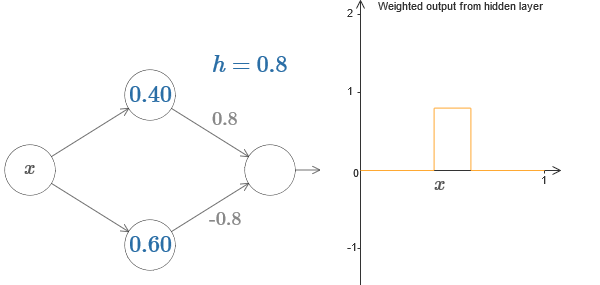
Tente aumentar e diminuir o valor h para ver como a altura da saliência muda. Tente fazer h negativo. Tente alterar os pontos das etapas para observar como isso muda a forma da saliência.

Você verá que usamos nossos neurônios não apenas como primitivas gráficas, mas também como unidades mais familiares aos programadores - algo como uma instrução if-then-else na programação:

se input> = início da etapa:
adicione 1 à saída ponderada
mais:
adicione 0 à saída ponderada

Na maior parte, vou me ater à notação gráfica. No entanto, às vezes será útil mudar para a exibição "se-então-outro" e refletir sobre o que está acontecendo nesses termos.

Podemos usar nosso truque de protrusão colando duas partes de neurônios ocultos na mesma rede:



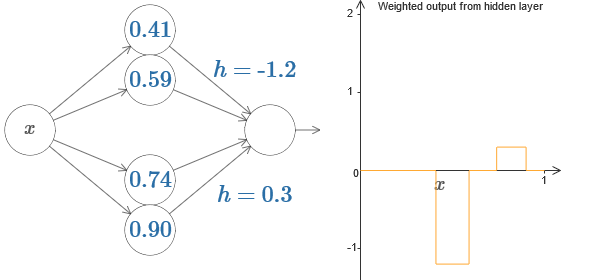
Aqui eu larguei os pesos simplesmente anotando os valores de h para cada par de neurônios ocultos. Tente jogar com ambos os valores de h e veja como isso muda o gráfico. Mova as guias, alterando os pontos das etapas.

Em um caso mais geral, essa ideia pode ser usada para obter qualquer número desejado de picos de qualquer altura. Em particular, podemos dividir o intervalo [0,1] em um grande número de (N) subintervalos e usar N pares de neurônios ocultos para obter picos de qualquer altura desejada. Vamos ver como isso funciona para N = 5. Isso já é um monte de neurônios, então eu sou uma apresentação um pouco mais restrita. Desculpe pelo diagrama complexo - eu poderia esconder a complexidade por trás de abstrações adicionais, mas parece-me que vale um pouco de tormento com complexidade, a fim de sentir melhor como as redes neurais funcionam.



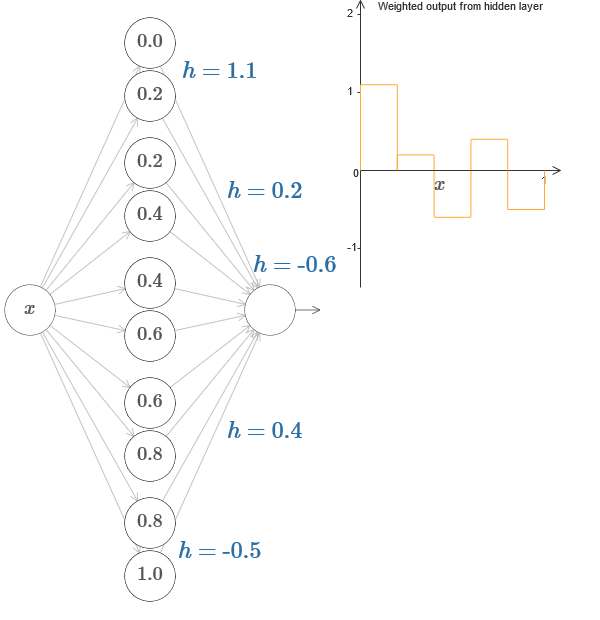
Veja bem, temos cinco pares de neurônios ocultos. Os pontos das etapas dos pares correspondentes estão localizados em 0,1 / 5, depois em 1 / 5,2 / 5 e assim por diante, até 4 / 5,5 / 5. Esses valores são fixos - obtemos cinco saliências de igual largura no gráfico.

Cada par de neurônios tem um valor h associado a ele. Lembre-se de que as conexões dos neurônios de saída têm pesos heh. No artigo original no gráfico, você pode clicar nos valores de h e movê-los para a esquerda-direita. Com uma mudança de altura, a programação também muda. Alterando os pesos de saída, construímos a função final!

No diagrama, você ainda pode clicar no gráfico e arrastar a altura das etapas para cima ou para baixo. Quando você altera sua altura, vê como a altura do h correspondente é alterada. Os pesos de saída + he –h mudam de acordo. Em outras palavras, manipulamos diretamente uma função cujo gráfico é mostrado à direita e vemos essas alterações nos valores de h à esquerda. Você também pode manter pressionado o botão do mouse em uma das saliências e arrastar o mouse para a esquerda ou direita, e as saliências serão ajustadas à altura atual.

É hora de fazer o trabalho.

Lembre-se da função que eu desenhei no início do capítulo:



Então eu não mencionei isso, mas na verdade é assim:

$$

$$f (x) = 0,2 + 0,4 x ^ 2 + 0,3x \ sin (15 x) + 0,05 \ cos (50 x) \ tag {113}$$

Ele é construído para valores x de 0 a 1, e os valores ao longo do eixo y variam de 0 a 1.

Obviamente, essa função não é trivial. E você precisa descobrir como calculá-lo usando redes neurais.

Nas redes neurais acima, analisamos uma combinação ponderada - _j w _j a _j da produção de neurônios ocultos. Sabemos como obter controle significativo sobre esse valor. Mas, como observei anteriormente, esse valor não é igual à saída da rede. A saída da rede é σ (w _j w _j a _j + b), onde b é o deslocamento do neurônio de saída. Podemos obter controle diretamente sobre a saída da rede?

A solução é desenvolver uma rede neural na qual a saída ponderada da camada oculta seja dada pela equação σ ⁻¹ ⋅ f (x), onde σ ⁻¹ é a função inversa de σ. Ou seja, queremos que a saída ponderada da camada oculta seja assim:



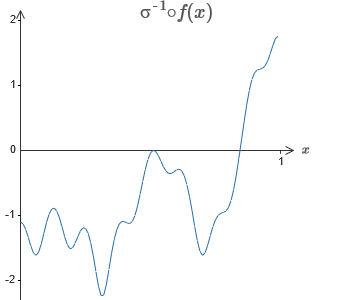Se isso der certo, a saída de toda a rede será uma boa aproximação de f (x) (defino o deslocamento do neurônio de saída como 0).

Então sua tarefa é desenvolver um NS que se aproxime da função objetivo mostrada acima. Para entender melhor o que está acontecendo, recomendo que você solucione esse problema duas vezes. Pela primeira vez no artigo original, clique no gráfico e ajuste diretamente as alturas das diferentes saliências. Será bastante fácil você obter uma boa aproximação à função objetivo. O grau de aproximação é estimado pelo desvio médio, a diferença entre a função objetivo e a função que a rede calcula. Sua tarefa é trazer o desvio médio para um valor mínimo. A tarefa é considerada concluída quando o desvio médio não excede 0,40.



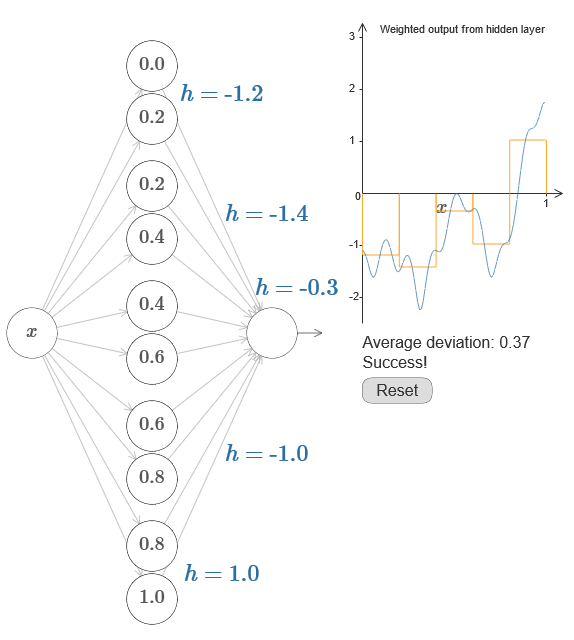Depois de obter sucesso, pressione o botão Redefinir, que altera as guias aleatoriamente. Na segunda vez, não toque no gráfico, mas altere os valores h no lado esquerdo do diagrama, tentando elevar o desvio médio para um valor de 0,40 ou menos.

E assim, você encontrou todos os elementos necessários para a rede calcular aproximadamente a função f (x)! A aproximação acabou sendo difícil, mas podemos melhorar facilmente o resultado simplesmente aumentando o número de pares de neurônios ocultos, o que aumentará o número de saliências.

Em particular, é fácil transformar todos os dados encontrados de volta na visualização padrão com a parametrização usada para o NS. Deixe-me lembrá-lo rapidamente de como isso funciona.

Na primeira camada, todos os pesos têm um grande valor constante, por exemplo, w = 1000.

Os deslocamentos dos neurônios ocultos são calculados através de b = −s. Assim, por exemplo, para o segundo neurônio oculto, s = 0,2 se transforma em b = -1000 × 0,2 = −200.

A última camada da escala é determinada pelos valores de h. Assim, por exemplo, o valor escolhido para o primeiro h, h = -0,2, significa que os pesos de saída dos dois neurônios ocultos superiores são -0,2 e 0,2, respectivamente. E assim por diante, para toda a camada de pesos de saída.

Finalmente, o deslocamento do neurônio de saída é 0.

E é isso: temos uma descrição completa do NS, que calcula bem a função objetivo inicial. E entendemos como melhorar a qualidade da aproximação, melhorando o número de neurônios ocultos.

Além disso, em nossa função objetivo original f (x) = 0,2 + 0,4x ²+ 0,3sin (15x) + 0,05cos (50x) não é nada de especial. Um procedimento semelhante pode ser usado para qualquer função contínua nos intervalos de [0,1] a [0,1]. De fato, usamos nosso NS de camada única para criar uma tabela de pesquisa para uma função. E podemos tomar essa idéia como base para obter uma prova generalizada da universalidade.

Função de muitos parâmetros

Estendemos nossos resultados ao caso de um conjunto de variáveis ​​de entrada. Parece complicado, mas todas as idéias que precisamos já podem ser entendidas para o caso com apenas duas variáveis ​​recebidas. Portanto, consideramos o caso com duas variáveis ​​recebidas.

Vamos começar examinando o que acontece quando um neurônio tem duas entradas: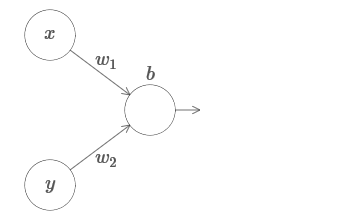



Temos entradas x e y, com os pesos correspondentes w ₁ e w ₂ e deslocamento b do neurônio. Definimos o peso de w ₂ como 0 e brincamos com o primeiro, w ₁ , e deslocamos b para ver como eles afetam a saída do neurônio:



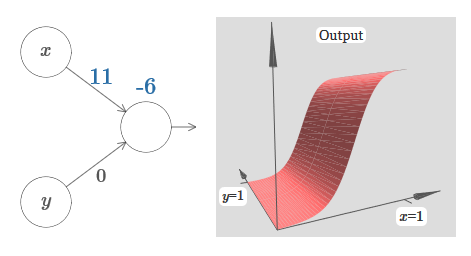Como você pode ver, com w ₂ = 0, a entrada y não afeta a saída do neurônio. Tudo acontece como se x fosse a única entrada.

Diante disso, o que você acha que acontecerá quando aumentarmos o peso de w ₁ a w ₁ = 100 e w ₂ deixar 0? Se isso não estiver claro imediatamente, pense um pouco sobre esse problema. Assista ao vídeo a seguir, que mostra o que vai acontecer:



Como antes, com um aumento no peso de entrada, a saída se aproxima da forma da etapa. A diferença é que nossa função de etapa agora está localizada em três dimensões. Como antes, podemos mover a localização das etapas alterando o deslocamento. O ângulo estará no ponto s _x ≡ - b / w1.

Vamos refazer o diagrama para que o parâmetro seja o local da etapa:



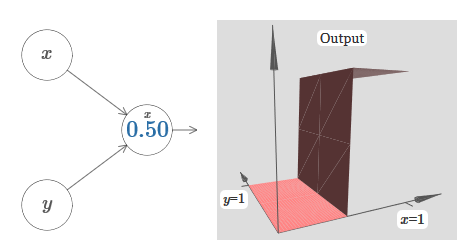Assumimos que o peso de entrada de x seja de grande importância - usei w ₁ = 1000 - e o peso w ₂ = 0. O número no neurônio é a posição do passo, e o x acima nos lembra que movemos o passo ao longo do eixo x. Naturalmente, é bem possível obter uma função de passo ao longo do eixo y, aumentando o peso recebido por y (por exemplo, w ₂= 1000), e o peso de x é 0, w ₁ = 0:



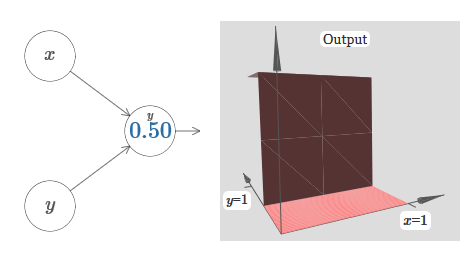O número no neurônio indica novamente a posição do passo, e y acima dele nos lembra que movemos o passo ao longo do eixo y. Eu poderia designar diretamente os pesos para x e y, mas não o fiz, porque isso iria desarrumar o gráfico. Mas lembre-se de que o marcador y indica que o peso de y é grande e de x é 0.

Podemos usar as funções de etapa que acabamos de projetar para calcular a função de protrusão tridimensional. Para fazer isso, usamos dois neurônios, cada um dos quais calculará uma função de etapa ao longo do eixo x. Em seguida, combinamos essas funções de etapa com os pesos heh, onde h é a altura de protrusão desejada. Tudo isso pode ser visto no diagrama a seguir:



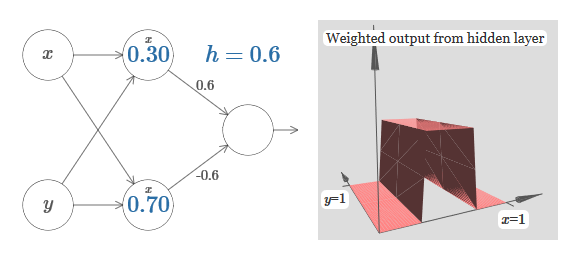Tente alterar o valor de h. Veja como isso se relaciona com os pesos da rede. E como ela altera a altura da função de protrusão à direita.

Tente também alterar o ponto da etapa, cujo valor é definido como 0,30 no neurônio oculto superior. Veja como ele muda a forma da saliência. O que acontece se você o mover além do ponto 0,70 associado ao neurônio oculto inferior?

Aprendemos como construir a função de protrusão ao longo do eixo x. Naturalmente, podemos facilmente fazer a função de protrusão ao longo do eixo y, usando duas funções de passo ao longo do eixo y. Lembre-se de que podemos fazer isso fazendo grandes pesos na entrada ye definindo o peso 0 na entrada x. E então, o que acontece:



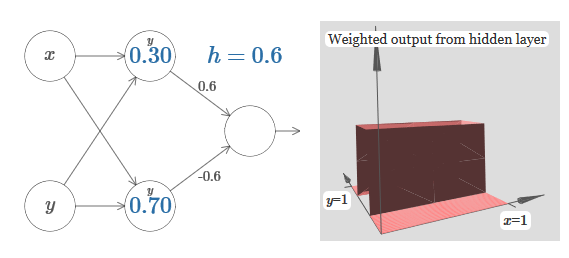Parece quase idêntico à rede anterior! A única mudança visível são pequenos marcadores nos neurônios ocultos. Eles nos lembram que produzem funções de passo para y, e não para x, portanto, o peso na entrada y é muito grande, e na entrada x é zero, e não vice-versa. Como antes, decidi não mostrá-lo diretamente, para não confundir a imagem.

Vamos ver o que acontece se adicionarmos duas funções de protrusão, uma ao longo do eixo x, a outra ao longo do eixo y, ambas de altura h:



Para simplificar o diagrama de conexão com peso zero, eu o omiti. Até agora, deixei pequenos marcadores x e y em neurônios ocultos para lembrar em quais direções as funções de protrusão são calculadas. Mais tarde, nós os recusaremos, pois eles estão implícitos na variável de entrada.

Tente alterar o parâmetro h. Como você pode ver, por causa disso, os pesos de saída mudam, assim como os pesos de ambas as funções de protrusão, xey.

Nossa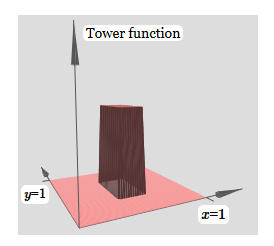



criação é um pouco como uma "função de torre": se podemos criar essas funções de torre, podemos usá-las para aproximar funções arbitrárias simplesmente adicionando torres de várias alturas em lugares diferentes:



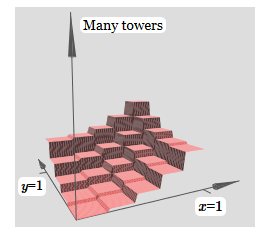é claro, ainda não alcançamos a criação de uma função de torre arbitrária. Até agora, construímos algo como uma torre central de altura 2h, com um platô de altura h ao seu redor.

Mas podemos fazer uma torre funcionar. Lembre-se de que mostramos anteriormente como os neurônios podem ser usados ​​para implementar a instrução if-then-else:

if  >= :  1 else:  0 

Era um neurônio de uma entrada. E precisamos aplicar uma idéia semelhante à produção combinada de neurônios ocultos:

  if     >= :  1 else:  0 

Se escolhermos o limiar certo - por exemplo, 3h / 2, espremido entre a altura do platô e a altura da torre central - podemos esmagar o platô até zero e deixar apenas uma torre.

Imagine como fazer isso? Tente experimentar a seguinte rede. Agora, estamos plotando a saída de toda a rede, e não apenas a saída ponderada da camada oculta. Isso significa que adicionamos o termo de deslocamento à saída ponderada da camada oculta e aplicamos o sigmóide. Você pode encontrar os valores de he para os quais você obtém uma torre? Se você ficar preso nesse momento, aqui estão duas dicas: (1) para o neurônio de saída mostrar um comportamento se-então-outro, precisamos que os pesos recebidos (todos h ou –h) sejam grandes; (2) o valor de b determina a escala do limiar se-então-outro.



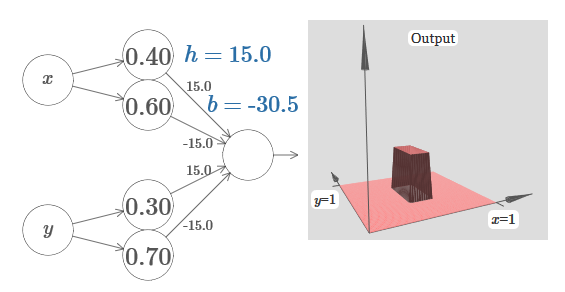
Com parâmetros padrão, a saída é semelhante a uma versão nivelada do diagrama anterior, com uma torre e um platô. Para obter o comportamento desejado, você precisa aumentar o valor de h. Isso nos dará o comportamento do limite do if-then-else. Em segundo lugar, para definir corretamente o limite, é necessário escolher b −3h / 2.

Aqui está o que parece para h = 10:


Mesmo para valores relativamente modestos de h, obtemos uma boa função de torre. E, é claro, podemos obter um resultado arbitrariamente bonito aumentando h ainda mais e mantendo o viés no nível b = −3h / 2.

Vamos tentar colar duas redes para contar duas funções diferentes da torre. Para esclarecer os respectivos papéis das duas sub-redes, coloquei-os em retângulos separados: cada um deles calcula a função da torre usando a técnica descrita acima. O gráfico à direita mostra a saída ponderada da segunda camada oculta, ou seja, a combinação ponderada das funções da torre.



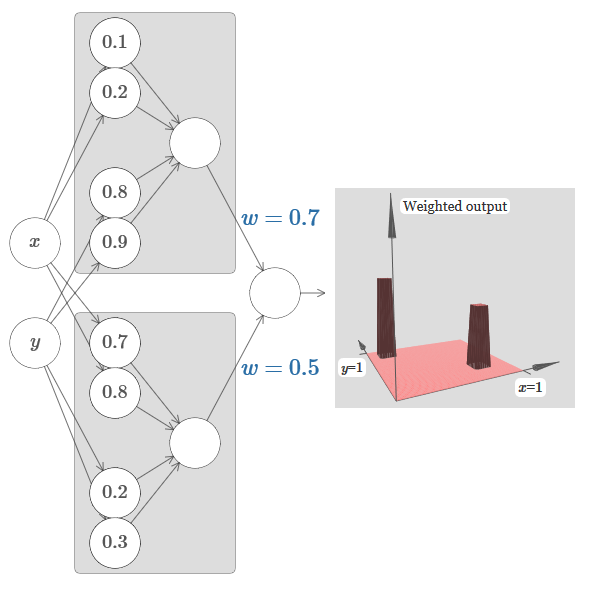
Em particular, pode-se observar que, alterando o peso na última camada, é possível alterar a altura das torres de saída.

A mesma idéia permite que você calcule quantas torres quiser. Podemos torná-los arbitrariamente magros e altos. Como resultado, garantimos que a saída ponderada da segunda camada oculta se aproxime de qualquer função desejada de duas variáveis:



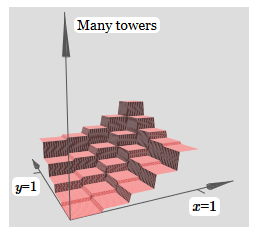
Em particular, fazendo com que a saída ponderada da segunda camada oculta se aproxime σ ⁻¹ ⋅ de poço, garantimos que a saída da nossa rede seja uma boa aproximação da função desejada f.

E as funções de muitas variáveis?

Vamos tentar pegar três variáveis, x ₁ , x ₂ , x ₃ . A rede a seguir pode ser usada para calcular a função da torre em quatro dimensões?



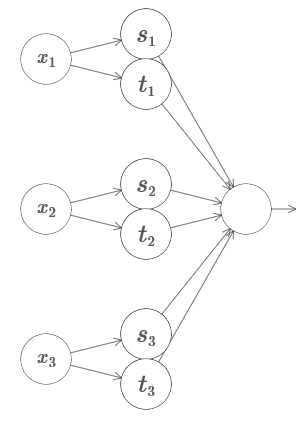
Aqui x ₁ , x ₂ , x ₃ denotam a entrada de rede. s ₁ , t ₁ e assim por diante - os pontos de referência para os neurônios - ou seja, todos os pesos na primeira camada são grandes e as compensações são atribuídas para que os pontos de referência sejam s ₁ , t ₁ , s ₂ , ... Os pesos na segunda camada se alternam, + h, −h, onde h é um número muito grande. O deslocamento da saída é de -5h / 2.

A rede calcula uma função igual a 1 em três condições: x ₁ está entre s ₁ e t ₁ ; x2 está entre s2 e t2; x ₃ está entre s ₃ e t ₃ . A rede é 0 em todos os outros lugares. Esta é uma torre na qual 1 é uma pequena porção do espaço de entrada e 0 é todo o resto.

Ao colar muitas dessas redes, podemos obter quantas torres quisermos e aproximar uma função arbitrária de três variáveis. A mesma idéia funciona em m dimensões. Somente o deslocamento da saída (−m + 1/2) h é alterado para comprimir adequadamente os valores desejados e remover o platô.

Bem, agora sabemos como usar o NS para aproximar a função real de muitas variáveis. E as funções vetoriais f (x ₁ , ..., x _m ) ∈ R ⁿ ? Obviamente, essa função pode ser considerada simplesmente como n funções reais separadas f1 (x ₁ , ..., x _m ), f2 (x ₁ , ..., x _m ) e assim por diante. E então apenas colamos todas as redes juntas. Portanto, é fácil descobrir isso.

Desafio

• Vimos como usar redes neurais com duas camadas ocultas para aproximar uma função arbitrária. Você pode provar que isso é possível com uma camada oculta? Dica - tente trabalhar com apenas duas variáveis ​​de saída e mostre que: (a) é possível obter as funções das etapas não apenas ao longo dos eixos x ou y, mas também em uma direção arbitrária; (b) somando muitas construções da etapa (a), é possível aproximar a função de uma torre redonda e não retangular; © usando torres redondas, é possível aproximar uma função arbitrária. A etapa © será mais fácil de usar usando o material apresentado neste capítulo, um pouco abaixo.

Indo além dos neurônios sigmóides

Provamos que uma rede de neurônios sigmóides pode calcular qualquer função. Lembre-se de que em um neurônio sigmóide, as entradas x ₁ , x ₂ , ... se transformam na saída em σ (w _j w _j x _{j j} + b), onde w _j são os pesos, b é o viés e σ é o sigmóide.



E se olharmos para outro tipo de neurônio usando uma função de ativação diferente, s (z):



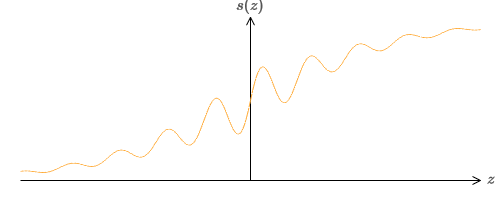
Ou seja, assumimos que se um neurônio tem x ₁ , x ₂ , ... pesos w ₁ , w ₂ , ... e viés b, então s (∑ _j w _j x _j + b) será emitido.

Nós podemos usar esta função de ativação para sermos pisados, assim como no caso do sigmóide. Tente (no artigo original ) no diagrama elevar o peso para, digamos, w = 100:





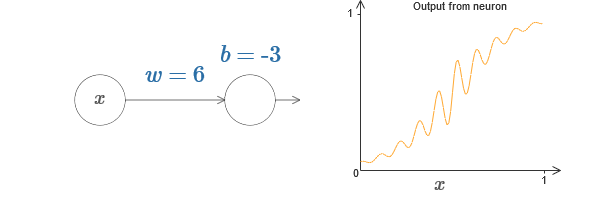
Como no caso do sigmóide, por causa disso, a função de ativação é compactada e, como resultado, se transforma em uma aproximação muito boa da função de passo. Tente alterar o deslocamento, e você verá que podemos alterar a localização da etapa para qualquer. Portanto, podemos usar todos os mesmos truques de antes para calcular qualquer função desejada.

Quais propriedades s (z) devem ter para que isso funcione? Precisamos assumir que s (z) está bem definido como z → − e z → ∞. Esses limites são dois valores aceitos pela nossa função step. Também precisamos assumir que esses limites são diferentes. Se eles não diferissem, as etapas não funcionariam; simplesmente haveria um horário fixo! Mas se a função de ativação s (z) satisfaz essas propriedades, os neurônios baseados nela são universalmente adequados para cálculos.

As tarefas

• No início do livro, encontramos um tipo diferente de neurônio - um neurônio linear endireitado ou uma unidade linear retificada, ReLU. Explique por que esses neurônios não satisfazem as condições necessárias para a universalidade. Encontre evidências de versatilidade, mostrando que as ReLUs são universalmente adequadas para computação.
• Suponha que estamos considerando neurônios lineares, com a função de ativação s (z) = z. Explique por que os neurônios lineares não satisfazem as condições da universalidade. Mostre que esses neurônios não podem ser usados ​​para computação universal.

Função de correção de etapa

Por enquanto, assumimos que nossos neurônios produzem funções precisas de passos. Esta é uma boa aproximação, mas apenas uma aproximação. De fato, há uma lacuna estreita de falha, mostrada no gráfico a seguir, onde as funções não se comportam como uma função de etapa:



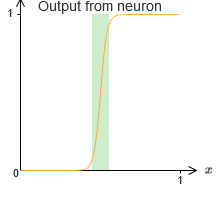
Nesse período de fracasso, minha explicação da universalidade não funciona.

O fracasso não é tão assustador. Ao definir pesos de entrada suficientemente grandes, podemos reduzir esses espaços arbitrariamente pequenos. Podemos torná-los muito menores do que no gráfico, invisíveis aos olhos. Talvez não tenhamos que nos preocupar com esse problema.

No entanto, eu gostaria de ter uma maneira de resolvê-lo.

Acontece que é fácil de resolver. Vamos analisar esta solução para calcular as funções do NS com apenas uma entrada e saída. As mesmas idéias trabalharão para resolver o problema com um grande número de entradas e saídas.

Em particular, suponha que queremos que nossa rede calcule alguma função f. Como antes, tentamos fazer isso projetando a rede para que a saída ponderada da camada oculta de neurônios seja σ ⁻¹ ⋅ f (x):



Se fizermos isso usando a técnica descrita acima, forçaremos os neurônios ocultos a produzir uma sequência de funções de protrusão:



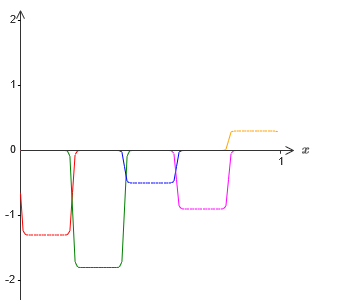
É claro que exagerei o tamanho dos intervalos de falha, para que fosse mais fácil ver. Deve ficar claro que, se somarmos todas essas funções das saliências, obteremos uma aproximação bastante boa de σ ⁻¹ ⋅ f (x) em todos os lugares, exceto nos intervalos de falha.

Mas suponha que, em vez de usar a aproximação descrita, usamos um conjunto de neurônios ocultos para calcular a aproximação de metade da nossa função objetivo original, ou seja, σ ⁻¹ ⋅ f (x) / 2. Obviamente, será parecido com uma versão em escala do gráfico mais recente:



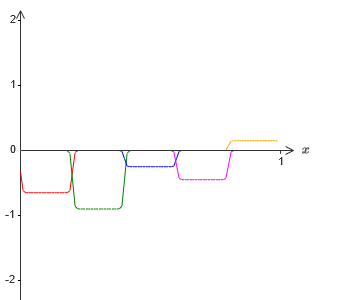
E suponha que façamos mais um conjunto de neurônios ocultos calcular a aproximação de σ ⁻¹ ⋅ f (x) / 2, no entanto, em sua base, as saliências serão deslocadas pela metade de sua largura:



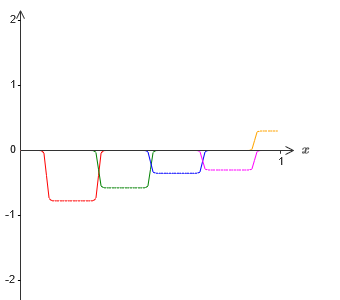
Agora temos duas aproximações diferentes para σ - 1⋅f (x) / 2. Se somarmos essas duas aproximações, obteremos uma aproximação geral para σ - 1⋅f (x). Essa aproximação geral ainda terá imprecisões em pequenos intervalos. Mas o problema será menor do que antes - porque os pontos que caem nos intervalos da falha da primeira aproximação não caem nos intervalos da falha da segunda aproximação. Portanto, a aproximação nesses intervalos será aproximadamente duas vezes melhor.

Podemos melhorar a situação adicionando um número grande, M, de aproximações sobrepostas da função σ - 1⋅f (x) / M. Se todos os intervalos de falha forem estreitos o suficiente, qualquer corrente estará em apenas um deles. Se você usar um número suficientemente grande de aproximações sobrepostas de M, o resultado será uma excelente aproximação geral.

Conclusão

A explicação da universalidade discutida aqui definitivamente não pode ser chamada de uma descrição prática de como contar funções usando redes neurais! Nesse sentido, é mais uma prova da versatilidade dos portões lógicos da NAND e muito mais. Portanto, eu basicamente tentei tornar esse design claro e fácil de seguir, sem otimizar seus detalhes. No entanto, tentar otimizar esse design pode ser um exercício interessante e instrutivo para você.

Embora o resultado obtido não possa ser usado diretamente para criar o NS, é importante porque remove a questão da computabilidade de qualquer função específica usando o NS. A resposta para essa pergunta sempre será positiva. Portanto, é correto perguntar se alguma função é computável, mas qual é a maneira correta de calculá-la.

Nosso design universal usa apenas duas camadas ocultas para calcular uma função arbitrária. Como discutimos, é possível obter o mesmo resultado com uma única camada oculta. Diante disso, você pode se perguntar por que precisamos de redes profundas, ou seja, redes com um grande número de camadas ocultas. Não podemos simplesmente substituir essas redes por redes rasas que possuem uma camada oculta?

Embora, em princípio, seja possível, existem boas razões práticas para o uso de redes neurais profundas. Conforme descrito no Capítulo 1, os NSs profundos têm uma estrutura hierárquica que lhes permite adaptar-se bem ao estudo do conhecimento hierárquico, que é útil para resolver problemas reais. Mais especificamente, ao resolver problemas como o reconhecimento de padrões, é útil usar um sistema que compreenda não apenas pixels individuais, mas também conceitos cada vez mais complexos: de bordas a formas geométricas simples e além, a cenas complexas envolvendo vários objetos. Em capítulos posteriores, veremos evidências a favor do fato de que NSs profundas serão mais capazes de lidar com o estudo de tais hierarquias de conhecimento do que as rasas. Resumindo: a universalidade nos diz que o NS pode calcular qualquer função; evidências empíricas sugerem que NSs profundas são melhor adaptadas ao estudo de funções úteis para resolver muitos problemas do mundo real.