Um novo método de análise de cluster é proposto. Sua vantagem está em um algoritmo menos complexo computacionalmente. O método é baseado no cálculo de votos para o fato de um par de objetos estar na mesma classe a partir de informações sobre o valor de coordenadas individuais.
1. Introdução
Uma grande necessidade de análise de dados é o desenvolvimento de métodos eficazes de classificação. Em tais métodos, é necessário dividir todo o conjunto de objetos no número ideal de classes, com base apenas em informações sobre o valor de indicadores individuais [Zagoruyko 1999].
A análise de cluster é um dos métodos mais populares de análise de dados e estatística matemática. A análise de cluster permite que você encontre automaticamente classes de objetos, usando apenas informações sobre os indicadores quantitativos de objetos (treinamento sem professor). Cada classe pode ser definida por um de seus objetos mais característicos, por exemplo, média em termos de indicadores. Há um grande número de métodos e abordagens para classificar dados.
Pesquisas modernas no campo da análise de cluster são realizadas para aprimorar métodos para determinar classes de topologia complexa [Furaoa 2007, Zagoruiko 2013], bem como para melhorar a velocidade dos algoritmos no caso de big data.
Neste artigo, propomos um método de classificação baseado na obtenção de votos para um par de objetos da mesma classe, com base em informações sobre o valor de indicadores individuais. Propõe-se considerar que um par de objetos está na mesma classe se os valores de seus indicadores individuais estiverem no intervalo com um comprimento que não exceda um determinado valor.
Método K-means
O método k-means é um dos métodos de cluster mais populares. Seu objetivo é obter esses datacenters que corresponderiam à hipótese de compactação de classes de dados com sua distribuição radial simétrica. Uma maneira de determinar as posições de tais centros, dado seu número \ textit {k}, é a abordagem EM.
Neste método, dois procedimentos são executados sequencialmente.
- Definição para cada objeto de dados $ inline $ X_ {i} $ inline $ o centro mais próximo $ inline $ C_ {j} $ inline $ e atribuindo um rótulo de classe a este objeto $ inline $ X_ {i} ^ {j} $ inline $ . Além disso, para todos os objetos, sua pertença a diferentes classes torna-se determinada.
- Cálculo da nova posição dos centros de todas as classes.
Repetindo iterativamente esses dois procedimentos a partir da posição aleatória inicial dos centros das classes \ textit {k}, podemos conseguir a separação de objetos em classes que corresponderiam mais de perto à hipótese de compactação radial das classes.
O algoritmo de classificação de um novo autor será comparado com o método k-means.
Novo método
O novo algoritmo de análise de cluster é construído com base em votos por pertencer a diferentes clusters a partir de informações sobre os valores das coordenadas individuais dos pontos de dados.
- Um valor d é especificado que caracteriza a duração do intervalo de indicadores dentro do qual dois objetos são considerados pertencentes à mesma classe.
- Métrica selecionada $ inline $ x_ {i} $ inline $ e todos os pares de objetos são considerados $ inline $ \ left \ {O_ {l}, O_ {k} \ right \} $ inline $ onde $ inline $ l, k = 1 \ ldots N $ inline $ .
- Se $ inline $ \ left | x_ {i} ^ {l} -x_ {i} ^ {k} \ right | \ le d $ inline $ então a magnitude $ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (voz adicionada).
- As ações 2) e 3) são repetidas para todos os indicadores $ inline $ i = 1 \ ldots M $ inline $ .
- É definido o valor p que caracteriza o número mínimo de votos por pertencer às mesmas classes.
- Usando o método-chave de pares de valores, todas as classes de objetos são determinadas, de modo que dentro de uma classe de voz para pares de objetos dessas classes > = p .
- Repete todos os valores de d e repete os itens 1) - 6) para obter o número de classes mais próximo do número determinado de classes g .
Para reduzir a complexidade do algoritmo para
N , você pode usar intervalos
T para indicadores individuais e substituir a cláusula 2) e 3) no algoritmo pelo seguinte:
1. O indicador está selecionado
$ inline $ x_ {i} $ inline $ e todos os intervalos são considerados
$ inline $ \ left [u_ {l}, w_ {l} \ right] $ inline $ onde
$ inline $ l = 1 \ ldots T $ inline $ :
$$ exibição $$ u_ {0} = \ min (x_ {i}); u_ {0} = \ min (x_ {i}); $$ exibição $$
$$ display $$ w_ {T} = \ max (x_ {i}); $$ display $$
$$ display $$ s_ {i} = w_ {T} -u_ {0}; $$ display $$
$$ display $$ u_ {l} = u_ {0} + l \ cdot s_ {i}; $$ display $$
$$ display $$ w_ {l} = u_ {l} + d; $$ display $$
2. Se
$ inline $ x_ {i} ^ {k} \ in \ left [u_ {j}, w_ {j} \ right] $ inline $ e
$ inline $ x_ {i} ^ {l} \ in \ left [u_ {j}, w_ {j} \ right] $ inline $ onde
$ inline $ j = 1 \ ldots T $ inline $ então a magnitude
$ inline $ r_ {lk}: = r_ {lk} + 1 $ inline $ (a voz é adicionada com uma tecla única
l ,
k para o
i- ésimo indicador).
Experiência numérica
Os dados com a classificação intuitiva para humanos foram tomados como dados iniciais.
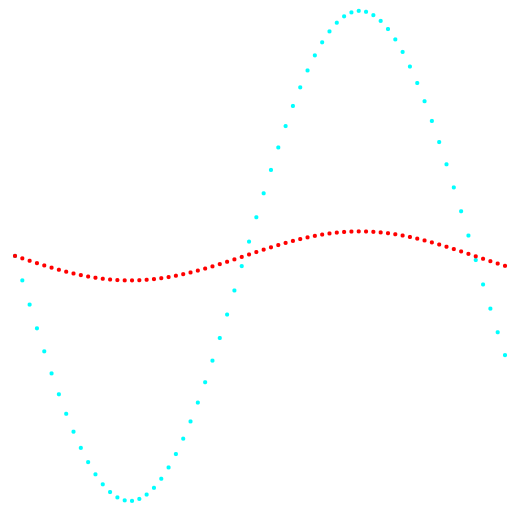
As figuras 1 e 2 mostram os resultados da classificação do método das médias k e do novo método de classificação.
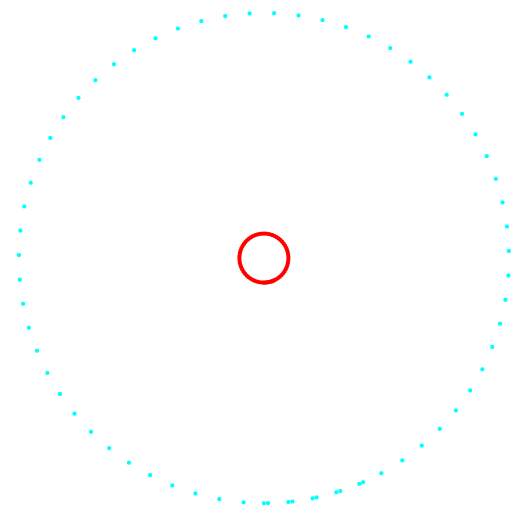Fig. 1. Projeção 1-2 e classificação dos dados.À esquerda está o método k-means, à direita está o método do autor.
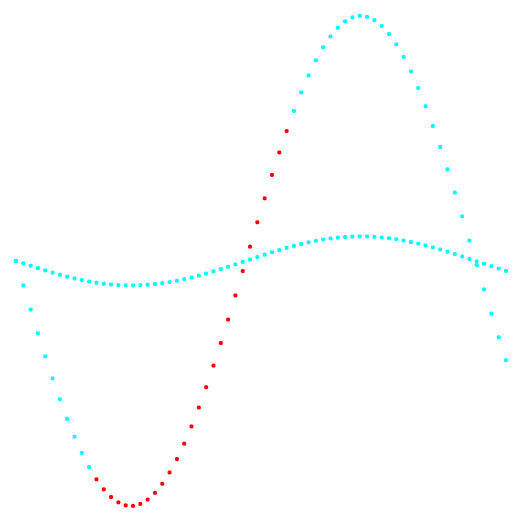
Fig. 2. Projeção 2-3 e classificação dos dados.À esquerda está o método k-means, à direita está o método do autor.
O resultado da comparação dos dois métodos mostra a vantagem óbvia do método do autor em sua capacidade de detectar clusters de topologia complexa.
Implementação de software
O método de agrupamento k-means foi implementado programaticamente como um aplicativo da web. A parte de computação do aplicativo é enviada para um servidor escrito em PHP usando a estrutura Zend. A interface do aplicativo é escrita usando HTML, CSS, JavaScript, jQuery. O aplicativo está disponível em
http://svlaboratory.org/application/klaster2 após registrar um novo usuário. O aplicativo permite visualizar a pertença de objetos a diferentes agrupamentos em um determinado plano de coordenadas.
Conclusão
Um novo método de classificação é proposto. As vantagens desse método são o reconhecimento de classes de topologia complexa, distribuição não radial, bem como menor complexidade do algoritmo e menos ações, o que é especialmente benéfico no caso de grandes matrizes de dados.
Referências- Zagoruyko N.G. Métodos aplicados de análise de dados e conhecimento. Novosibirsk: Editora do Instituto de Matemática, 1999.270 p.
- Zagoruyko N.G., Borisova I.A., Kutnenko O.A., Levanov D.A. Detecção de padrões em matrizes de dados experimentais // Tecnologias computacionais. - 2013. Vol. 18. Não. S1. S. 12-20.
- Shen Furaoa, Tomotaka Ogurab, Osamu Hasegawab Uma rede neural incremental auto-organizada aprimorada para aprendizado on-line não supervisionado. Hasegawa Lab, 2007.