A tradução foi preparada para os alunos do curso "Applied Analytics on R" .
Esta foi minha primeira tentativa de agrupar clientes com base em dados reais e me proporcionou uma experiência valiosa. Existem muitos artigos na Internet sobre clustering usando variáveis numéricas, mas encontrar soluções para dados categóricos, o que é um pouco mais difícil, não era tão simples. Os métodos de clustering para dados categóricos ainda estão em desenvolvimento e, em outro post, tentarei outro.
Por outro lado, muitas pessoas pensam que o agrupamento de dados categóricos pode não produzir resultados significativos - e isso é parcialmente verdade (consulte a
excelente discussão sobre CrossValidated ). A certa altura, pensei: “O que estou fazendo? Eles podem simplesmente ser divididos em coortes. ” No entanto, a análise de coorte também nem sempre é aconselhável, especialmente com um número significativo de variáveis categóricas com um grande número de níveis: você pode lidar facilmente com 5-7 coortes, mas se você tiver 22 variáveis e cada uma tiver 5 níveis (por exemplo, uma pesquisa de cliente com estimativas discretas 1 , 2, 3, 4 e 5), e você precisa entender quais grupos característicos de clientes você está lidando - você obterá coortes 22x5. Ninguém quer se preocupar com essa tarefa. E aqui o agrupamento pode ajudar. Portanto, nesta postagem, falarei sobre o que eu gostaria de saber assim que comecei a agrupar.
O próprio processo de armazenamento em cluster consiste em três etapas:
- Construir uma matriz de dissimilaridade é sem dúvida a decisão mais importante no agrupamento. Todas as etapas subsequentes serão baseadas na matriz de dissimilaridade que você criou.
- A escolha do método de agrupamento.
- Avaliação de cluster.
Este post será um tipo de introdução que descreve os princípios básicos do clustering e sua implementação no ambiente R.
Matriz de dissimilaridade
A base para o agrupamento será a matriz de dissimilaridade, que em termos matemáticos descreve quão diferentes os pontos no conjunto de dados são (removidos) um do outro. Permite combinar ainda mais nos grupos os pontos mais próximos um do outro ou separar os mais distantes entre si - essa é a principal idéia do agrupamento.
Nesse estágio, as diferenças entre os tipos de dados são importantes, uma vez que a matriz de dissimilaridade é baseada nas distâncias entre os pontos de dados individuais. É fácil imaginar as distâncias entre os pontos dos dados numéricos (um exemplo bem conhecido são as
distâncias euclidianas ), mas no caso de dados categóricos (fatores em R), tudo não é tão óbvio.
Para construir uma matriz de dissimilaridade nesse caso, deve-se usar a chamada distância de Gover. Não vou me aprofundar na parte matemática desse conceito, simplesmente fornecerei links:
aqui e
ali . Para isso, prefiro usar
daisy() com a
metric = c("gower") do pacote de
cluster .
A matriz de dissimilaridade está pronta. Para 200 observações, ele é construído rapidamente, mas pode exigir uma quantidade muito grande de computação se você estiver lidando com um grande conjunto de dados.
Na prática, é muito provável que você primeiro precise limpar o conjunto de dados, executar as transformações necessárias das linhas em fatores e rastrear os valores ausentes. No meu caso, o conjunto de dados também continha linhas de valores ausentes que foram agrupados maravilhosamente a cada vez, por isso parecia um tesouro - até que eu olhei para os valores (infelizmente!).
Algoritmos de cluster
Você já deve saber que o clustering é
k-means e hierárquico . Neste post, focalizo o segundo método, já que é mais flexível e permite várias abordagens: você pode escolher o algoritmo de agrupamento
aglomerativo (de baixo para cima) ou
divisional (de cima para baixo).
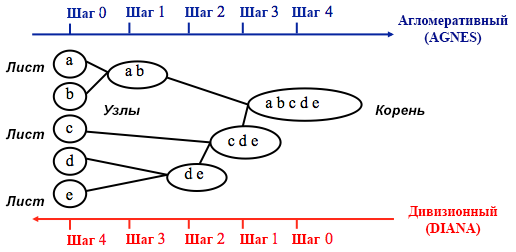Fonte: Guia de programação do UC Business Analytics RO agrupamento aglomerativo começa com
n agrupamentos, em que
n é o número de observações: assume-se que cada um deles é um agrupamento separado. Em seguida, o algoritmo tenta encontrar e agrupar os pontos de dados mais semelhantes entre si - é assim que a formação de cluster começa.
O agrupamento por divisão é realizado da maneira oposta - assume-se inicialmente que todos os n pontos de dados que temos são um cluster grande e, em seguida, os menos semelhantes são divididos em grupos separados.
Ao decidir qual desses métodos escolher, sempre faz sentido tentar todas as opções, no entanto, em geral, o
clustering aglomerativo é melhor para identificar pequenos agrupamentos e é usado pela maioria dos programas de computador, e o agrupamento por divisão é mais apropriado para identificar agrupamentos grandes .
Pessoalmente, antes de decidir qual método usar, prefiro olhar para os dendrogramas - uma representação gráfica do agrupamento. Como você verá mais adiante, alguns dendrogramas são bem equilibrados, enquanto outros são muito caóticos.
# A entrada principal para o código abaixo é a diferença (matriz de distância)
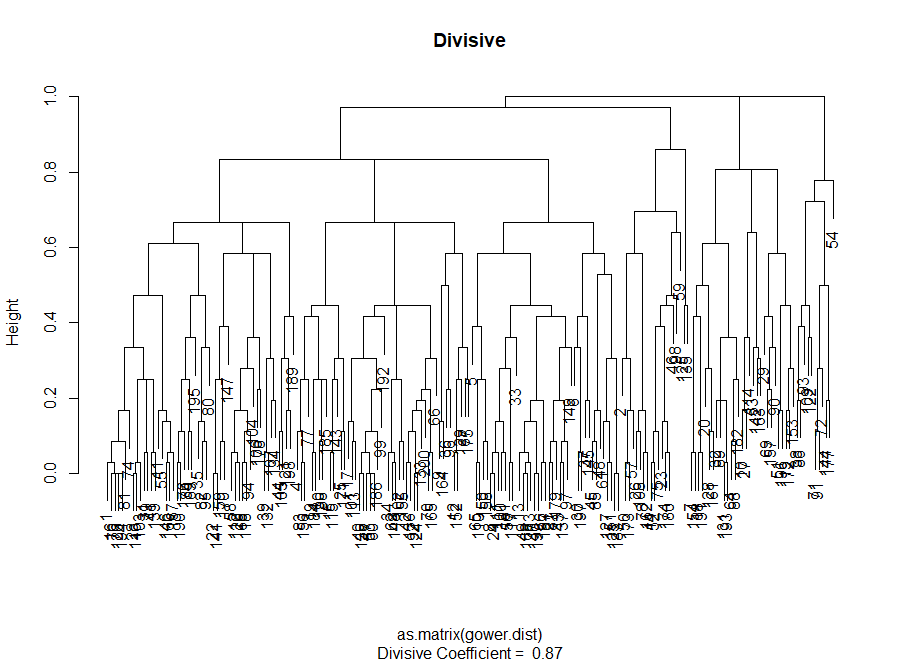
Avaliação de qualidade de cluster
Nesse estágio, é necessário escolher entre diferentes algoritmos de armazenamento em cluster e um número diferente de clusters. Você pode usar diferentes métodos de avaliação, sem esquecer de ser guiado pelo
senso comum . Eu destaquei essas palavras em negrito e itálico, porque a
importância da escolha é
muito importante - o número de clusters e o método de dividir os dados em grupos devem ser práticos do ponto de vista prático. O número de combinações de valores de variáveis categóricas é finito (uma vez que são discretos), mas nenhum detalhamento baseado nelas será significativo. Você também pode não querer ter muito poucos clusters - nesse caso, eles serão muito generalizados. No final, tudo depende do seu objetivo e das tarefas da análise.
Em geral, ao criar clusters, você está interessado em obter grupos de pontos de dados claramente definidos, para que a distância entre esses pontos dentro do cluster (
ou compactação ) seja mínima e a distância entre grupos (
separabilidade ) seja a máxima possível. Isso é fácil de entender intuitivamente: a distância entre os pontos é uma medida de sua dissimilaridade, obtida com base na matriz de dissimilaridade. Assim, a avaliação da qualidade do agrupamento é baseada na avaliação da compactação e separabilidade.
A seguir, demonstrarei duas abordagens e mostrarei que uma delas pode fornecer resultados sem sentido.
- Método do cotovelo : comece com ele se o fator mais importante para sua análise for a compactação dos clusters, ou seja, a semelhança entre os grupos.
- Método de avaliação de silhuetas : O gráfico de silhueta usado como uma medida da consistência dos dados mostra o quão perto cada ponto de um cluster está dos pontos nos clusters vizinhos.
Na prática, esses dois métodos geralmente oferecem resultados diferentes, o que pode levar a alguma confusão - a compactação máxima e a separação mais clara serão alcançadas com um número diferente de clusters, de modo que o bom senso e a compreensão do que seus dados realmente significam desempenharão um papel importante ao tomar uma decisão final.
Há também várias métricas que você pode analisar. Vou adicioná-los diretamente ao código.
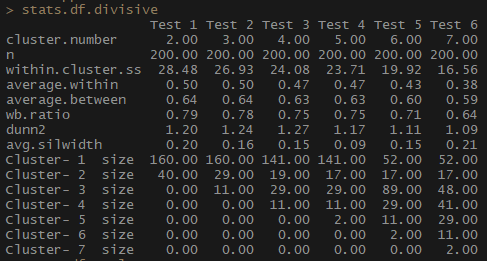
Portanto, o indicador average.within, que representa a distância média entre as observações nos clusters, diminui, assim como within.cluster.ss (a soma dos quadrados das distâncias entre as observações em um cluster). A largura média da silhueta (avg.silwidth) não muda de maneira tão inequívoca; no entanto, um relacionamento inverso ainda pode ser percebido.
Observe como os tamanhos de cluster são desproporcionais. Eu não me apressaria a trabalhar com um número incomparável de observações dentro de clusters. Uma das razões é que o conjunto de dados pode estar desequilibrado e um grupo de observações supera todos os outros na análise - isso não é bom e provavelmente levará a erros.
stats.df.aggl <-cstats.table(gower.dist, aggl.clust.c, 7) #stats.df.aggl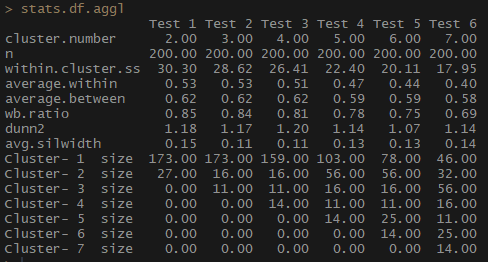
Observe quão melhor o número de observações por grupo é balanceado por cluster hierárquico aglomerativo com base no método de comunicação completo.
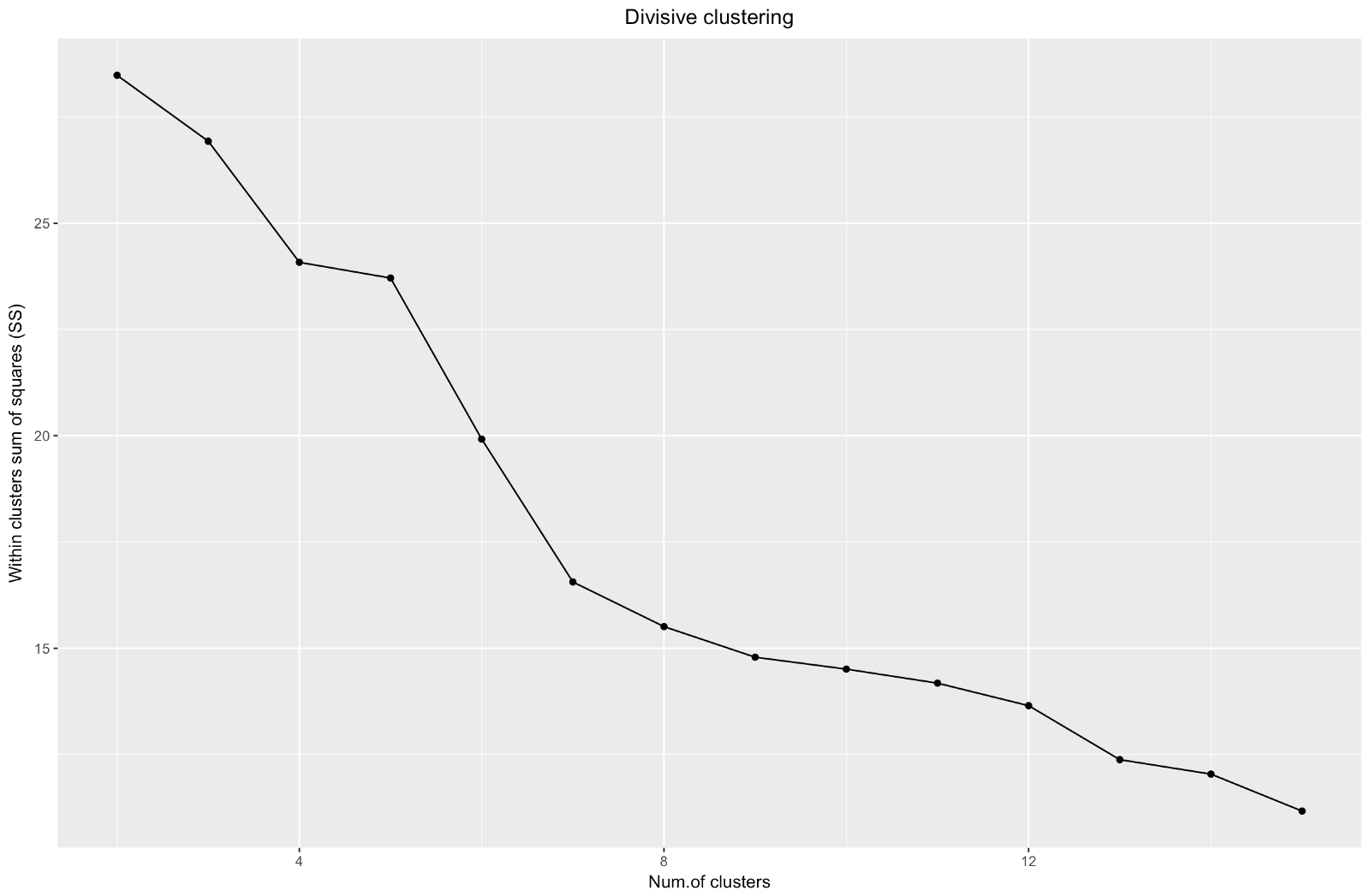
Então, criamos um gráfico do "cotovelo". Ele mostra como a soma das distâncias quadradas entre as observações (nós a usamos como uma medida da proximidade das observações - quanto menor, mais próximas são as medidas dentro do cluster) para um número diferente de clusters. Idealmente, devemos ver uma distinta “curva do cotovelo” no ponto em que aglomerados adicionais dão apenas uma ligeira diminuição na soma dos quadrados (SS). Para o gráfico abaixo, eu pararia em cerca de 7. Embora neste caso, um dos clusters seja composto por apenas duas observações. Vamos ver o que acontece durante o agrupamento aglomerado.
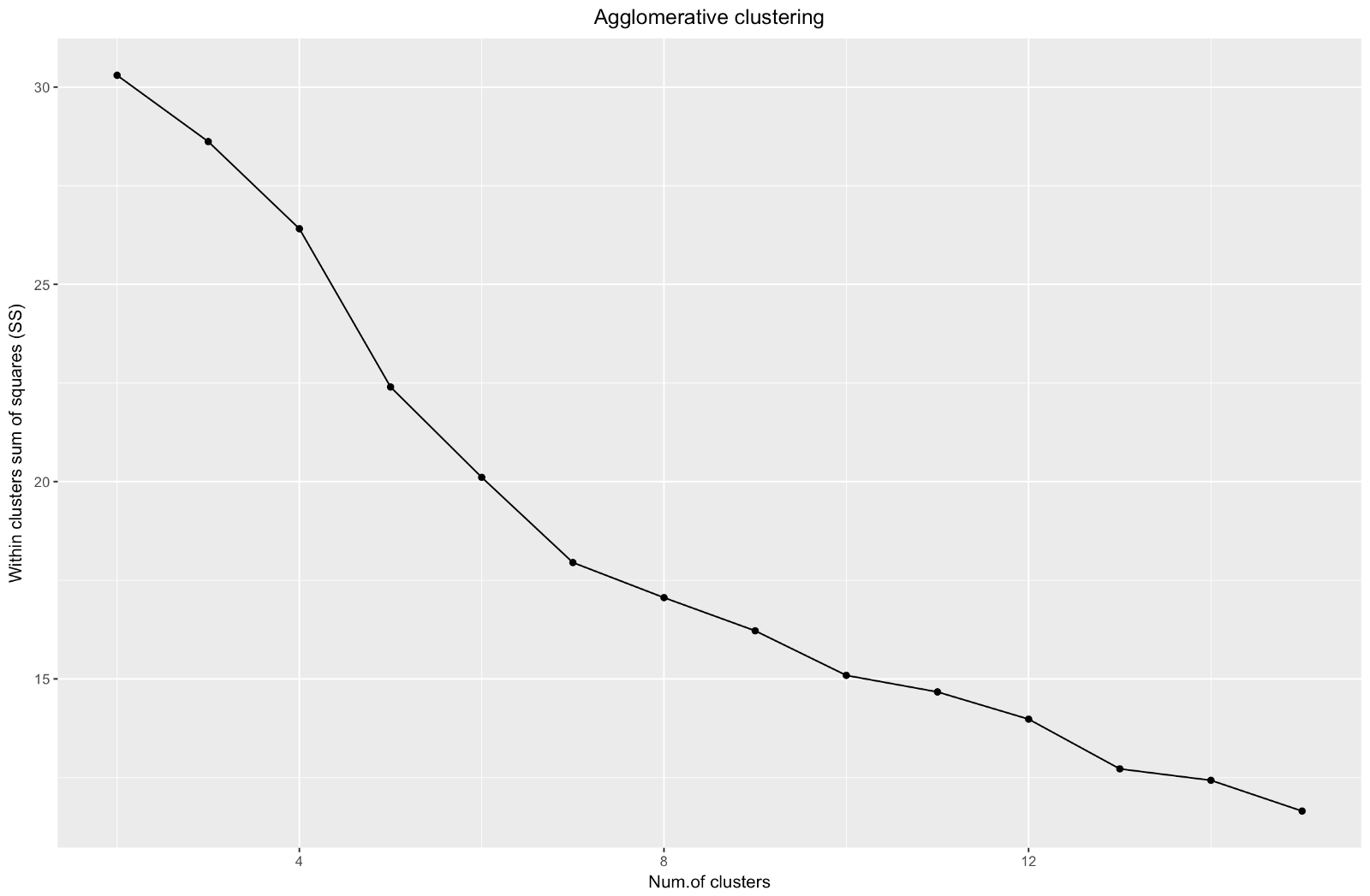
O “cotovelo” aglomerativo é semelhante ao da divisão, mas o gráfico parece mais suave - as curvas não são tão pronunciadas. Assim como no agrupamento por divisão, eu focaria em 7 agrupamentos, no entanto, ao escolher entre esses dois métodos, gosto mais dos tamanhos de agrupamento que são obtidos pelo método aglomerativo - é melhor que sejam comparáveis entre si.
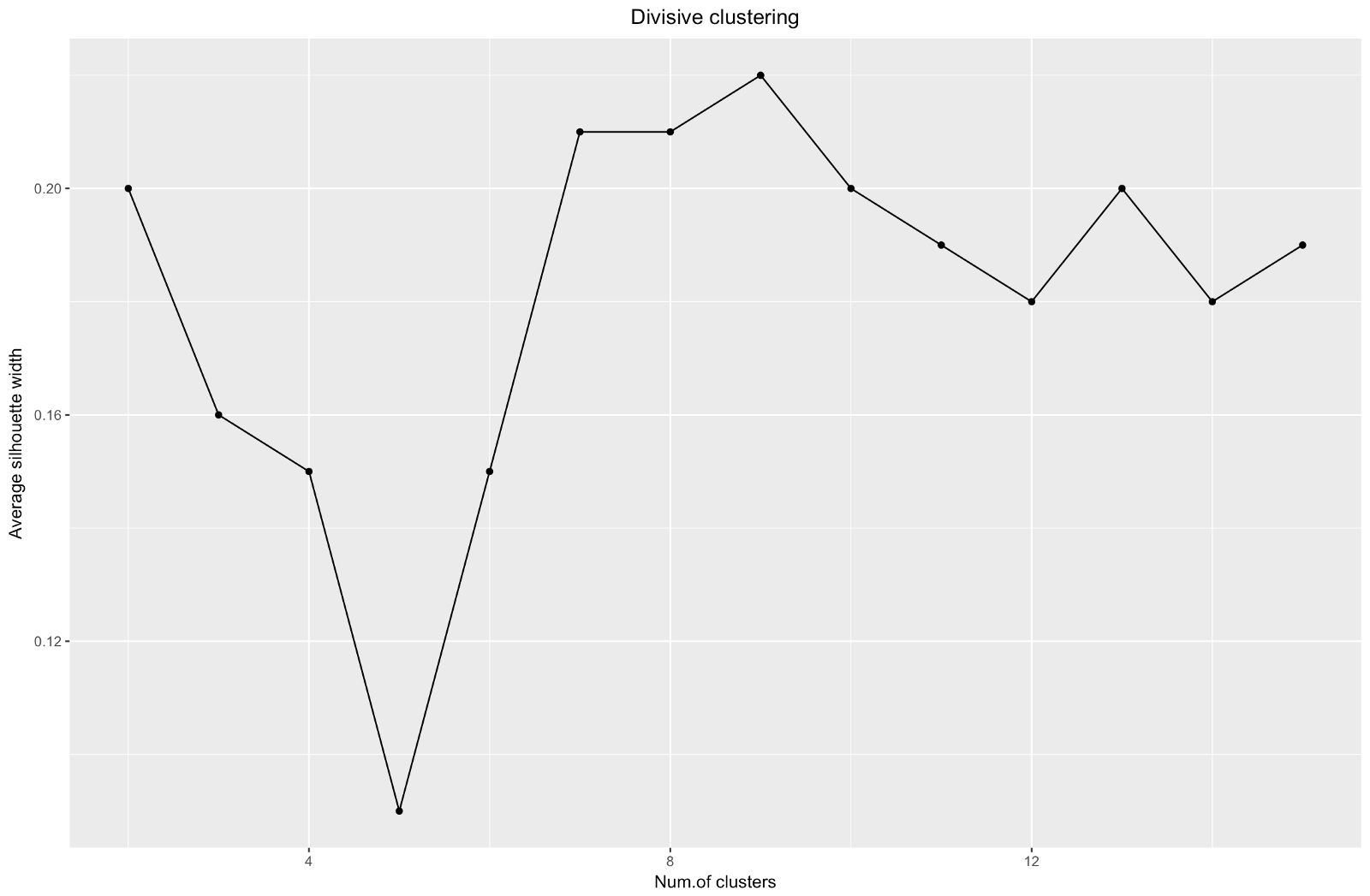
Ao usar o método de estimativa de silhueta, você deve escolher a quantidade que fornecer o coeficiente máximo de silhueta, porque você precisa de clusters suficientemente afastados para serem considerados separados.
O coeficiente da silhueta pode variar de –1 a 1, com 1 correspondendo a boa consistência dentro dos clusters e –1 não muito bom.
No caso do gráfico acima, você escolheria 9 em vez de 5 clusters.
Para comparação: no caso “simples”, o gráfico da silhueta é semelhante ao gráfico abaixo. Não é como o nosso, mas quase.
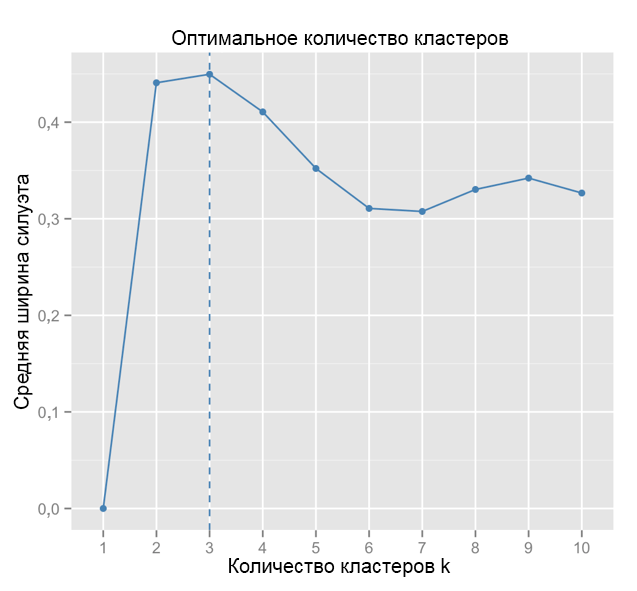Fonte: Marinheiros de Dados ggplot(data = data.frame(t(cstats.table(gower.dist, aggl.clust.c, 15))), aes(x=cluster.number, y=avg.silwidth)) + geom_point()+ geom_line()+ ggtitle("Agglomerative clustering") + labs(x = "Num.of clusters", y = "Average silhouette width") + theme(plot.title = element_text(hjust = 0.5))
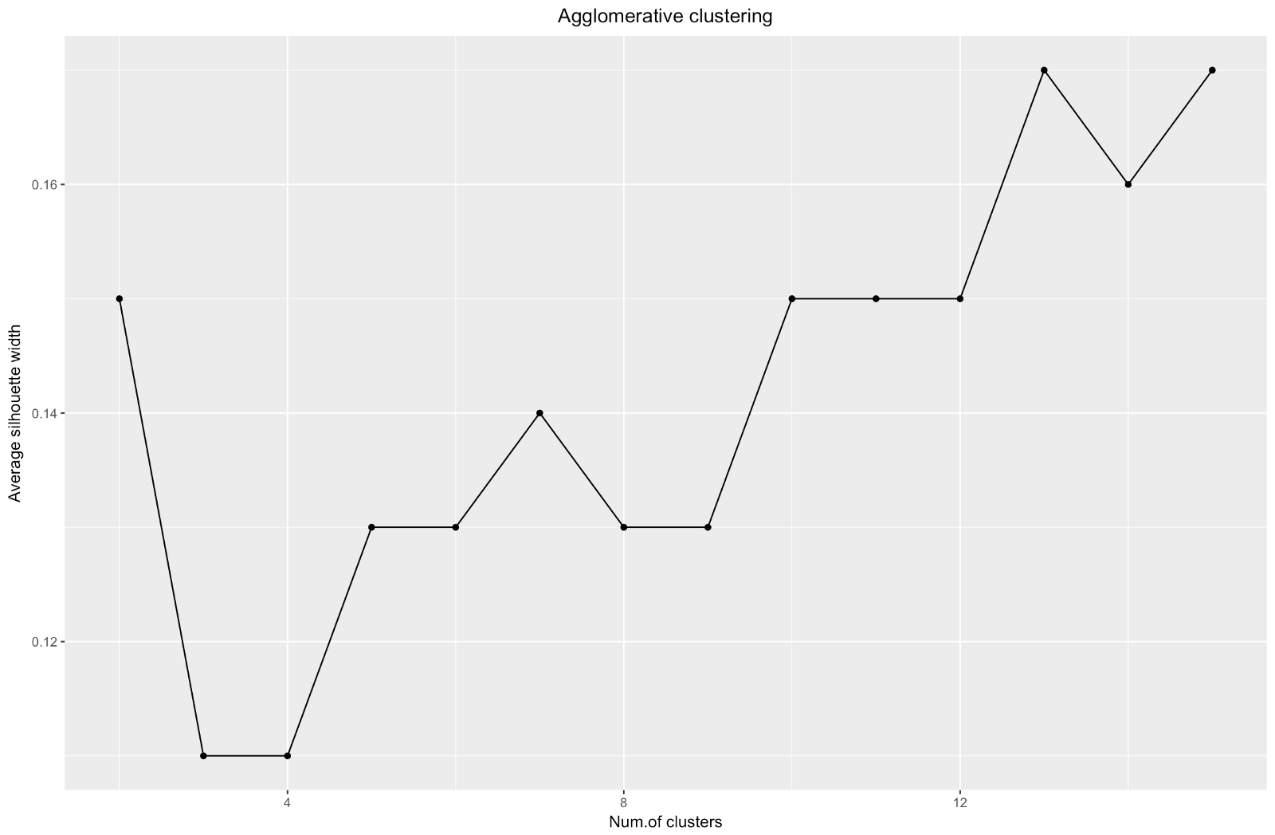
O gráfico de largura da silhueta nos diz: quanto mais você divide o conjunto de dados, mais claros os clusters se tornam. No entanto, no final, você alcançará pontos individuais e não precisará disso. No entanto, é exatamente isso que você verá se começar a aumentar o número de clusters
k . Por exemplo, para
k=30 obtive o seguinte gráfico:
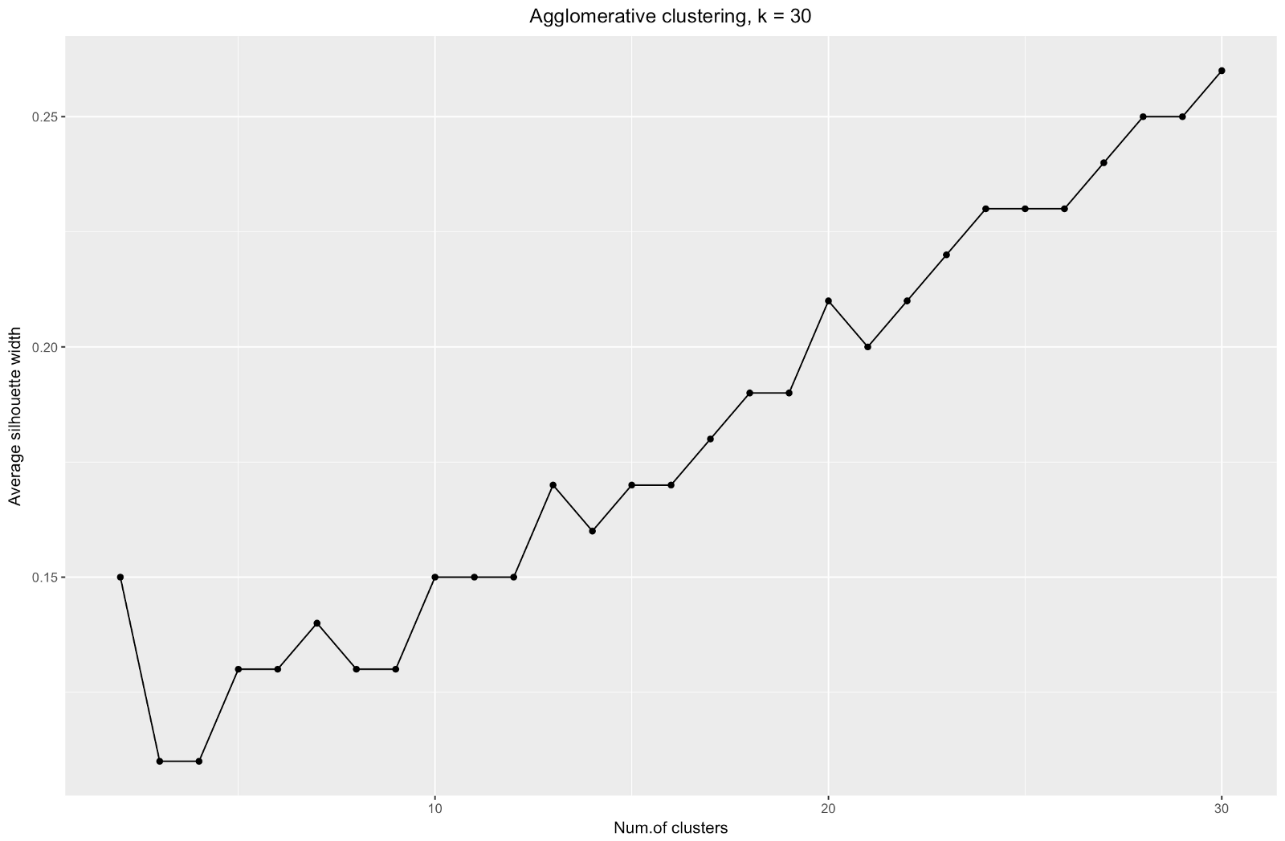
Para resumir: quanto mais você divide o conjunto de dados, melhores são os clusters, mas não podemos alcançar pontos individuais (por exemplo, no gráfico acima, selecionamos 30 clusters e temos apenas 200 pontos de dados).
Portanto, o agrupamento aglomerativo no nosso caso me parece muito mais equilibrado: os tamanhos dos agrupamentos são mais ou menos comparáveis (basta olhar para um agrupamento de apenas duas observações ao dividir pelo método de divisão!), E eu pararia em 7 agrupamentos obtidos por esse método. Vamos ver como eles se parecem e do que são feitos.
O conjunto de dados consiste em 6 variáveis que precisam ser visualizadas em 2D ou 3D, para que você tenha que trabalhar duro! A natureza dos dados categóricos também impõe algumas limitações, portanto, soluções prontas podem não funcionar. Eu preciso: a) ver como as observações são divididas em grupos; b) entender como as observações são categorizadas. Portanto, criei a) um dendograma de cores, b) um mapa de calor do número de observações por variável dentro de cada cluster.
library("ggplot2") library("reshape2") library("purrr") library("dplyr")
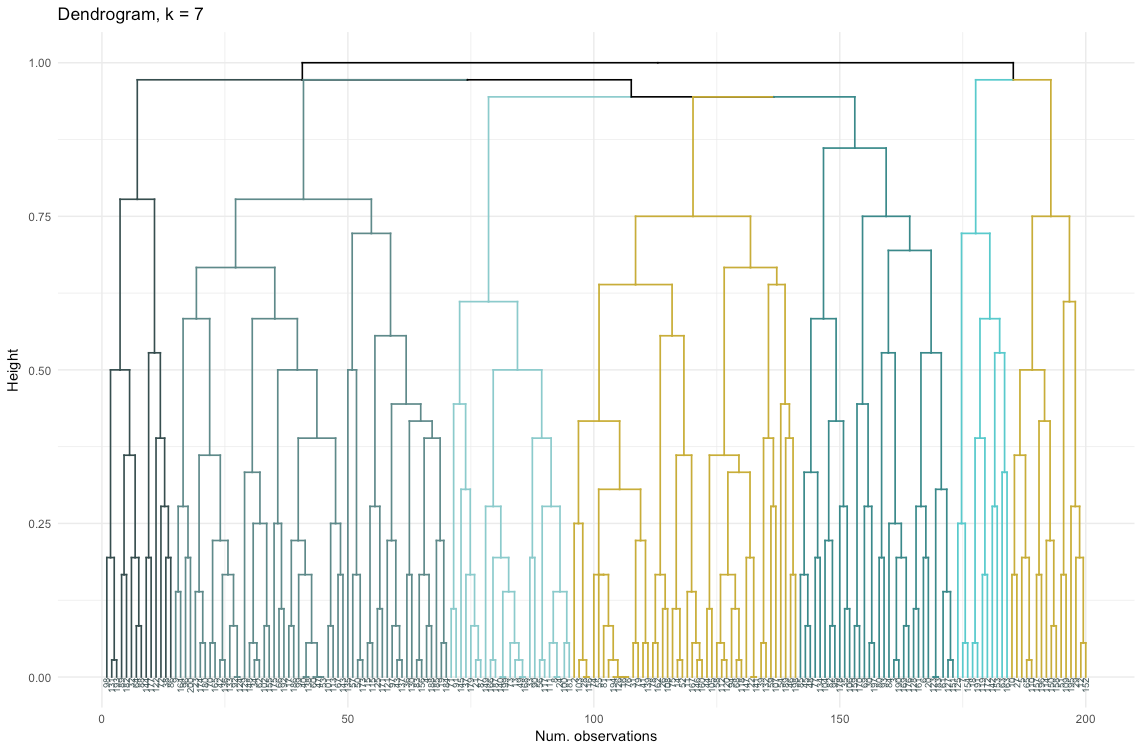
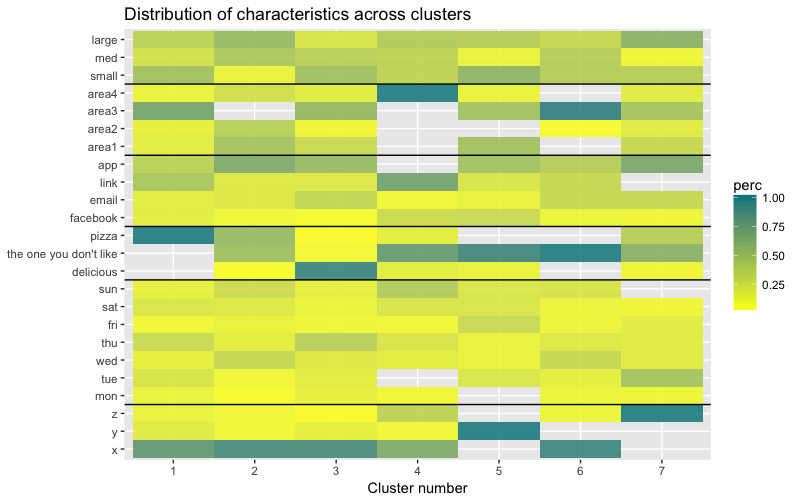
O mapa de calor mostra graficamente quantas observações são feitas para cada nível de fator para os fatores iniciais (as variáveis com as quais começamos). A cor azul escuro corresponde a um número relativamente grande de observações dentro do cluster. Esse mapa de calor também mostra que, para o dia da semana (dom, sáb ... seg) e o tamanho da cesta (grande, médio e pequeno), o número de clientes em cada célula é quase o mesmo - isso pode significar que essas categorias não são determinantes para a análise Talvez eles não precisem ser levados em consideração.
Conclusão
Neste artigo, calculamos a matriz de dissimilaridade, testamos os métodos aglomerativos e de divisão de agrupamento hierárquico e nos familiarizamos com os métodos de cotovelo e silhueta para avaliar a qualidade dos clusters.
O cluster hierárquico de divisão e aglomeração é um bom começo para estudar o tópico, mas não pare por aí se você realmente deseja dominar a análise de cluster. Existem muitos outros métodos e técnicas. A principal diferença dos dados numéricos em cluster é o cálculo da matriz de dissimilaridade. Ao avaliar a qualidade do agrupamento, nem todos os métodos padrão fornecerão resultados confiáveis e significativos - o método da silhueta provavelmente não é adequado.
E, finalmente, já que já passou algum tempo desde que eu fiz esse exemplo, agora vejo várias deficiências em minha abordagem e ficarei feliz em receber algum feedback. Um dos problemas significativos da minha análise não estava relacionado ao agrupamento como tal -
meu conjunto de dados estava desequilibrado de várias maneiras e esse momento permaneceu inexplicado. Isso teve um efeito notável no agrupamento: 70% dos clientes pertenciam a um nível do fator “cidadania”, e esse grupo dominou a maioria dos clusters obtidos, por isso era difícil calcular as diferenças em outros níveis do fator. Na próxima vez, tentarei equilibrar o conjunto de dados e comparar os resultados do cluster. Mas mais sobre isso em outro post.
Por fim, se você deseja clonar meu código, aqui está o link para o github:
https://github.com/khunreus/cluster-categoricalEspero que você tenha gostado deste artigo!
Fontes que me ajudaram:
Guia hierárquico de armazenamento em cluster (preparação de dados, armazenamento em cluster, visualização) - este blog será interessante para quem estiver interessado em análise de negócios no ambiente R:
http://uc-r.imtqy.com/hc_clustering e
https: // uc-r. imtqy.com/kmeans_clusteringValidação de cluster:
http://www.sthda.com/english/articles/29-cluster-validation-essentials/97-cluster-validation-statistics-must-know-methods/( k-):
https://eight2late.wordpress.com/2015/07/22/a-gentle-introduction-to-cluster-analysis-using-r/denextend, :
https://cran.r-project.org/web/packages/dendextend/vignettes/introduction.html#the-set-function, :
https://www.r-statistics.com/2010/06/clustergram-visualization-and-diagnostics-for-cluster-analysis-r-code/:
https://jcoliver.imtqy.com/learn-r/008-ggplot-dendrograms-and-heatmaps.html,
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5025633/ ( GitHub:
https://github.com/khunreus/EnsCat ).