Redes neurais e aprendizado profundo, capítulo 5: por que as redes neurais profundas são tão difíceis de treinar?

Imagine que você é um engenheiro e foi solicitado a desenvolver um computador do zero. Quando você está sentado no escritório, está lutando para projetar circuitos lógicos, distribuir as válvulas AND, OR e assim por diante - e de repente seu chefe entra e conta as más notícias. O cliente acabou de adicionar um requisito inesperado ao projeto: o esquema de todo o computador deve ter no máximo duas camadas:



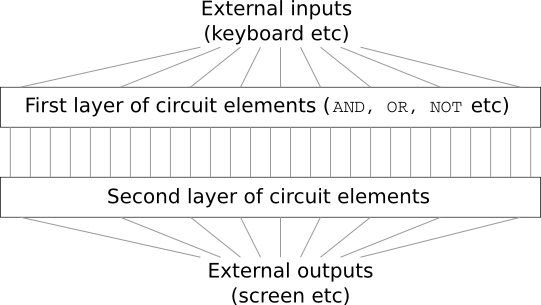
Você fica impressionado e diz ao chefe: "Sim, o cliente é louco!"

O chefe responde: “Eu também acho. Mas o cliente deve conseguir o que quer. "

De fato, em um sentido restrito, o cliente não é completamente louco. Suponha que você tenha permissão para usar um portão lógico especial que permita conectar qualquer número de entradas através de AND. E você tem permissão para usar a porta NAND com qualquer número de entradas, ou seja, uma porta que adicione muitas entradas através de AND e depois inverta o resultado. Acontece que, com essas válvulas especiais, você pode calcular qualquer função com apenas um circuito de duas camadas.

No entanto, apenas porque algo pode ser feito não significa que vale a pena fazer. Na prática, ao resolver problemas associados ao design de circuitos lógicos (e quase todos os problemas algorítmicos), geralmente começamos resolvendo subtarefas e, em seguida, montamos gradualmente uma solução completa. Em outras palavras, criamos uma solução através de muitos níveis de abstração.

Por exemplo, suponha que projetemos um circuito lógico para multiplicar dois números. É provável que desejemos construí-lo a partir de subcircuitos que implementam operações como a adição de dois números. Os subcircuitos de adição, por sua vez, consistirão em subcircuitos adicionando dois bits. Grosso modo, nosso esquema será semelhante a este:



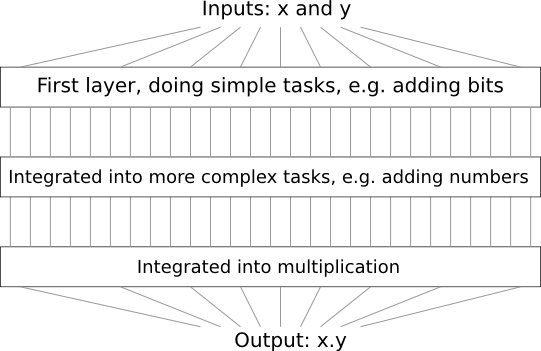
Ou seja, o último circuito contém pelo menos três camadas de elementos do circuito. De fato, provavelmente terá mais de três camadas quando dividirmos as subtarefas em menores do que aquelas que descrevi. Mas você entendeu o princípio.

Portanto, esquemas profundos facilitam o processo de design. Mas eles ajudam não apenas no design. Existem evidências matemáticas de que, para calcular algumas funções em circuitos muito rasos, é necessário o uso de um número exponencialmente maior de elementos do que nos profundos. Por exemplo, há uma famosa série de trabalhos científicos da década de 1980, nos quais foi demonstrado que o cálculo da paridade de um conjunto de bits requer um número exponencialmente maior de portas com um circuito raso. Por outro lado, ao usar esquemas profundos, é mais fácil calcular a paridade usando um esquema pequeno: você simplesmente calcula a paridade dos pares de bits e, em seguida, usa o resultado para calcular a paridade dos pares de bits e assim por diante, atingindo rapidamente a paridade geral. Portanto, esquemas profundos podem ser muito mais poderosos que os superficiais.

Até agora, este livro usou uma abordagem para redes neurais (NS), semelhante às solicitações de um cliente louco. Quase todas as redes com as quais trabalhamos tinham uma única camada oculta de neurônios (mais as camadas de entrada e saída):



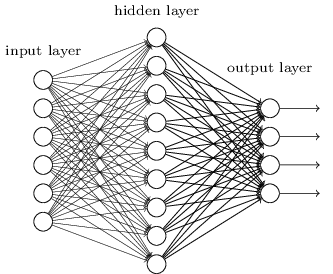
Essas redes simples se mostraram muito úteis: nos capítulos anteriores, usamos essas redes para classificar números manuscritos com uma precisão superior a 98%! No entanto, é intuitivamente claro que redes com muitas camadas ocultas serão muito mais poderosas:



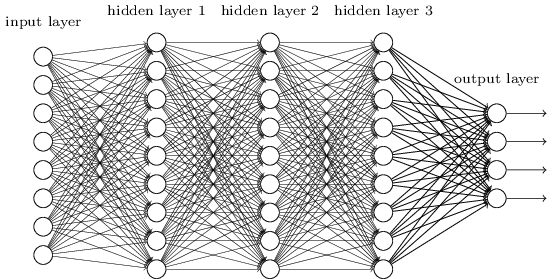
Essas redes podem usar camadas intermediárias para criar muitos níveis de abstração, como é o caso de nossos esquemas booleanos. Por exemplo, no caso do reconhecimento de padrões, os neurônios da primeira camada podem aprender a reconhecer faces, neurônios da segunda camada - formas mais complexas, por exemplo, triângulos ou retângulos criados a partir das faces. Então a terceira camada poderá reconhecer formas ainda mais complexas. E assim por diante É provável que essas muitas camadas de abstração ofereçam às redes profundas uma vantagem convincente na resolução de problemas de reconhecimento de padrões complexos. Além disso, como no caso de circuitos, existem resultados teóricos que confirmam que as redes profundas têm inerentemente mais recursos do que as rasas.

Como treinamos essas redes neurais profundas (GNSs)? Neste capítulo, tentaremos treinar STS usando nossa força de trabalho entre os algoritmos de treinamento - descida da propagação estocástica do gradiente para trás. No entanto, encontraremos um problema - nosso STS não funcionará muito melhor (se for ultrapassado) do que os rasos.

Essa falha parece estranha à luz da discussão acima. Mas, em vez de desistir do STS, vamos nos aprofundar no problema e tentar entender por que é difícil treiná-lo. Quando examinarmos de perto o problema, descobriremos que diferentes camadas no STS aprendem em velocidades muito diferentes. Em particular, quando as últimas camadas da rede são bem treinadas, as primeiras ficam presas durante o treinamento e aprendem quase nada. E não é apenas azar. Encontraremos razões fundamentais para desacelerar o aprendizado relacionadas ao uso de técnicas de aprendizado baseadas em gradiente.

Aprofundando-se nesse problema, descobrimos que o fenômeno oposto também pode ocorrer: as camadas iniciais podem aprender bem e as posteriores ficam presas. De fato, descobriremos a instabilidade interna associada ao treinamento de descida de gradiente em NSs multicamadas profundas. E devido a essa instabilidade, as camadas inicial ou tardia geralmente ficam presas no treinamento.

Tudo isso parece bastante desagradável. Mas, mergulhados nessas dificuldades, podemos começar a desenvolver idéias sobre o que precisa ser feito para o treinamento eficaz de STS. Portanto, esses estudos serão uma boa preparação para o próximo capítulo, onde usaremos o aprendizado profundo para abordar os problemas de reconhecimento de imagem.

Problema com gradiente de desvanecimento

Então, o que dá errado quando tentamos treinar uma rede profunda?

Para responder a essa pergunta, retornamos à rede que contém apenas uma camada oculta. Como sempre, usaremos o problema de classificação de dígitos do MNIST como uma caixa de areia para aprender e experimentar.

Se você deseja repetir todas essas etapas no seu computador, é necessário ter o Python 2.7 instalado, a biblioteca Numpy e uma cópia do código que pode ser obtido no repositório:

git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git 

Você pode ficar sem o git simplesmente baixando os dados e o código . Vá para o subdiretório src e, no shell python, carregue os dados MNIST:

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

Configure a rede:

 >>> import network2 >>> net = network2.Network([784, 30, 10]) 

Essa rede possui 784 neurônios na camada de entrada, correspondendo a 28 × 28 = 784 pixels da imagem de entrada. Utilizamos 30 neurônios ocultos e 10 fins de semana, correspondendo a dez opções de classificação possíveis para os números MNIST ('0', '1', '2', ..., '9').

Vamos tentar treinar nossa rede por 30 épocas inteiras usando mini-pacotes de 10 exemplos de treinamento por vez, aprendendo a velocidade η = 0,1 e o parâmetro de regularização λ = 5,0. Durante o treinamento, rastrearemos a precisão da classificação através de validation_data:

 >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Temos uma precisão de classificação de 96,48% (mais ou menos - os números variam com diferentes lançamentos), comparáveis ​​aos nossos resultados anteriores com configurações semelhantes.

Vamos adicionar outra camada oculta, também contendo 30 neurônios, e tentar treinar a rede com os mesmos hiperparâmetros:

 >>> net = network2.Network([784, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

A precisão da classificação melhora para 96,90%. É inspirador - um ligeiro aumento de profundidade ajuda. Vamos adicionar outra camada oculta de 30 neurônios:

 >>> net = network2.Network([784, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Não ajudou. O resultado caiu até 96,57%, valor próximo à rede rasa original. E se adicionarmos outra camada oculta:

 >>> net = network2.Network([784, 30, 30, 30, 30, 10]) >>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, ... evaluation_data=validation_data, monitor_evaluation_accuracy=True) 

Então a precisão da classificação cairá novamente, já para 96,53%. Estatisticamente, essa queda é provavelmente insignificante, mas não há nada de bom nisso.

Esse comportamento parece estranho. Parece intuitivamente que camadas ocultas adicionais devem ajudar a rede a aprender funções de classificação mais complexas e a lidar melhor com a tarefa. Obviamente, o resultado não deve piorar, porque, na pior das hipóteses, camadas adicionais simplesmente não farão nada. No entanto, isso não acontece.

Então o que está acontecendo? Vamos supor que camadas ocultas adicionais possam ajudar em princípio, e que o problema é que nosso algoritmo de treinamento não encontra os valores corretos para pesos e compensações. Gostaríamos de entender o que há de errado com nosso algoritmo e como melhorá-lo.

Para entender o que deu errado, vamos visualizar o processo de aprendizado de rede. Abaixo, construí uma parte da rede [784,30,30,10], na qual existem duas camadas ocultas, cada uma das quais com 30 neurônios ocultos. No diagrama, cada neurônio tem uma barra indicando a taxa de mudança no processo de aprendizado da rede. Uma barra grande significa que os pesos e deslocamentos do neurônio mudam rapidamente, e uma barra pequena significa que eles mudam lentamente. Mais precisamente, a barra denota o gradiente de ∂C / neurb do neurônio, ou seja, a taxa de mudança de custo em relação ao deslocamento. No capítulo 2, vimos que esse valor de gradiente controla não apenas a taxa de mudança de deslocamento durante o treinamento, mas também a taxa de alteração dos pesos dos neurônios de entrada. Não se preocupe se não conseguir se lembrar desses detalhes: basta ter em mente que essas barras indicam a rapidez com que os pesos e deslocamentos dos neurônios mudam durante o treinamento da rede.

Para simplificar o diagrama, desenhei apenas seis neurônios superiores em duas camadas ocultas. Abaixei os neurônios recebidos porque eles não têm pesos ou preconceitos. Omiti também os neurônios de saída, já que estamos comparando duas camadas, e faz sentido comparar camadas com o mesmo número de neurônios. O diagrama foi construído usando o programa generate_gradient.py no início do treinamento, ou seja, imediatamente após a inicialização da rede.



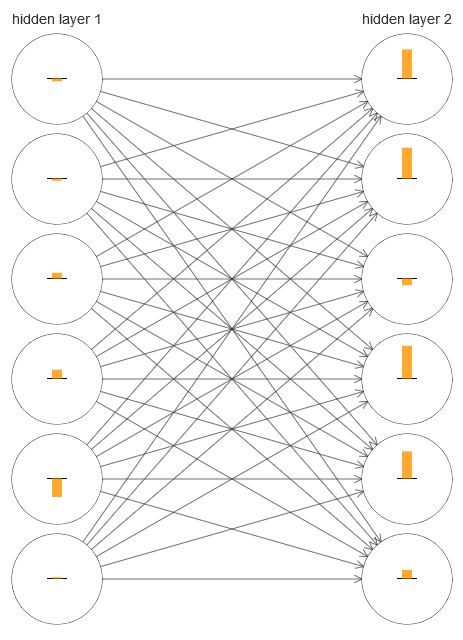
A rede foi inicializada por acaso, portanto, essa diversidade na velocidade de treinamento dos neurônios não é surpreendente. No entanto, chama a atenção imediatamente que, na segunda camada oculta, as tiras são basicamente muito mais do que na primeira. Como resultado, os neurônios na segunda camada aprenderão muito mais rápido que na primeira. Isso é uma coincidência ou é provável que os neurônios da segunda camada aprendam em geral mais rápido do que os neurônios da primeira?

Para saber exatamente, será bom ter uma maneira geral de comparar a velocidade de aprendizado na primeira e na segunda camadas ocultas. Para fazer isso, vamos denotar o gradiente como δ ^l _j = ∂C / ∂b ^l _j , isto é, como o gradiente do neurônio n. J na camada n. L. No segundo capítulo, chamamos isso de "erro", mas aqui chamarei informalmente de "gradiente". Informalmente - como esse valor não inclui explicitamente derivadas parciais do custo por peso, ∂C / ∂w. O gradiente δ ¹ pode ser pensado como um vetor cujos elementos determinam a rapidez com que a primeira camada oculta aprende e δ ² como um vetor cujos elementos determinam a rapidez com que a segunda camada oculta aprende. Usamos os comprimentos desses vetores como estimativas aproximadas da velocidade de aprendizado das camadas. Esse é, por exemplo, o comprimento || δ ¹ || mede a velocidade de aprendizado da primeira camada oculta e o comprimento || δ ² || mede a velocidade de aprendizado da segunda camada oculta.

Com essas definições e a mesma configuração acima, descobrimos que || δ ¹ || = 0,07 e || δ ² || = 0,31. Isso confirma nossas suspeitas: os neurônios da segunda camada oculta aprendem muito mais rápido que os neurônios da primeira camada oculta.

O que acontece se adicionarmos mais camadas ocultas? Com três camadas ocultas na rede [784,30,30,30,10], as velocidades de aprendizado correspondentes serão 0,012, 0,060 e 0,283. Novamente, as primeiras camadas ocultas aprendem muito mais lentamente que a anterior. Adicione outra camada oculta com 30 neurônios. Nesse caso, as velocidades de aprendizado correspondentes serão 0,003, 0,017, 0,070 e 0,285. O padrão é preservado: as camadas iniciais aprendem mais lentamente do que as posteriores.

Estudamos a velocidade de aprendizado desde o início - logo após a inicialização da rede. Como essa velocidade muda à medida que você aprende? Vamos voltar e olhar para a rede com duas camadas ocultas. A velocidade da aprendizagem muda assim:



Para obter esses resultados, usei descida de gradiente em lote com 1000 imagens de treinamento e treinamento por 500 épocas. Isso é um pouco diferente dos nossos procedimentos habituais - eu não usei mini-pacotes e tirei apenas 1000 imagens de treinamento, em vez de um conjunto completo de 50.000 peças. Não estou tentando enganar e enganar você, mas acontece que o uso da descida gradiente estocástica com minipacotes traz muito mais ruído aos resultados (mas se você calcular o ruído, os resultados serão semelhantes). Usando os parâmetros que escolhi, é fácil suavizar os resultados para que possamos ver o que está acontecendo.

De qualquer forma, como vemos, duas camadas começam a treinar em duas velocidades muito diferentes (o que já sabemos). Então, a velocidade de ambas as camadas cai muito rapidamente, após o que ocorre uma recuperação. No entanto, durante todo esse tempo, a primeira camada oculta aprende muito mais lentamente que a segunda.

E as redes mais complexas? Aqui estão os resultados de um experimento semelhante, mas com uma rede com três camadas ocultas [784,30,30,30,10]:



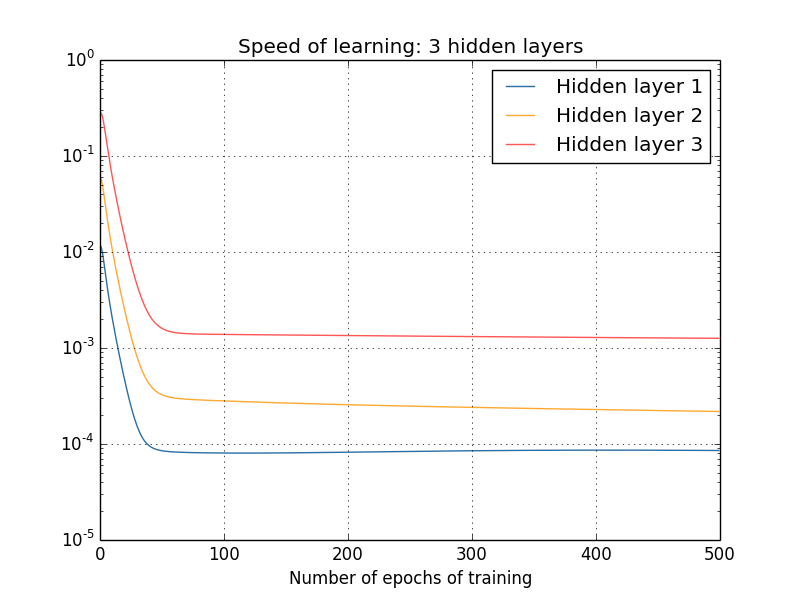
E, novamente, as primeiras camadas ocultas aprendem muito mais lentamente que a anterior. Por fim, vamos tentar adicionar uma quarta camada oculta (rede [784,30,30,30,30,10]) e ver o que acontece quando ele é treinado:



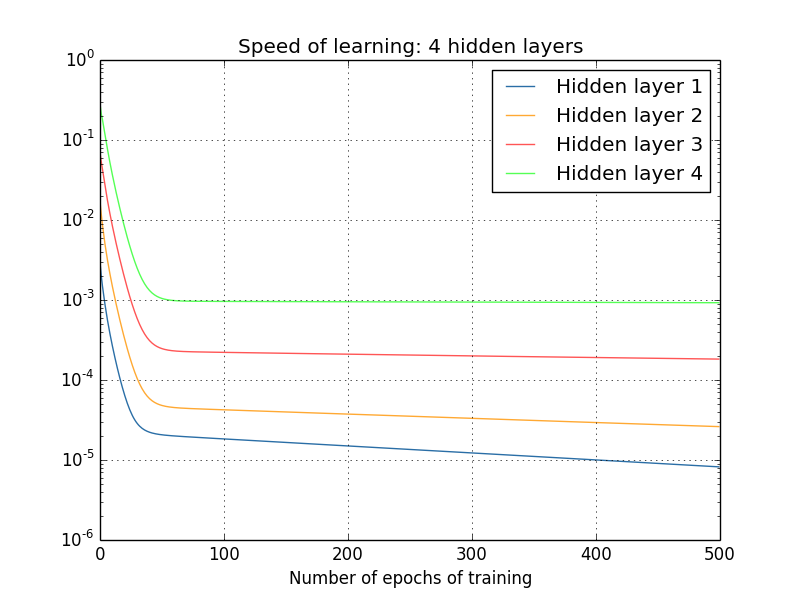
E, novamente, as primeiras camadas ocultas aprendem muito mais lentamente que a anterior. Nesse caso, a primeira camada oculta aprende cerca de 100 vezes mais lenta que a anterior. Não é de admirar que tenhamos tido problemas para aprender essas redes!

Fizemos uma observação importante: pelo menos em alguns GNSs, o gradiente diminui quando se move na direção oposta ao longo das camadas ocultas. Ou seja, os neurônios nas primeiras camadas são treinados muito mais lentamente do que os neurônios nas últimas. E, embora tenhamos observado esse efeito em apenas uma rede, há razões fundamentais para que isso ocorra em muitos NSs. Esse fenômeno é conhecido como "problema do gradiente de fuga" (ver obras 1 , 2 ).

Por que existe um problema de gradiente de desbotamento? Existem maneiras de evitá-lo? Como lidamos com isso ao treinar STS? De fato, logo descobriremos que isso não é inevitável, embora a alternativa não pareça muito atraente para ela: às vezes nas primeiras camadas o gradiente é muito maior! Isso já é um problema do crescimento explosivo do gradiente e não é mais bom do que no problema do gradiente que desaparece. Em geral, verifica-se que o gradiente no STS é instável e propenso a um crescimento explosivo ou a desaparecer nas primeiras camadas. Essa instabilidade é um problema fundamental para o treinamento gradiente de GNS. É isso que precisamos entender e, possivelmente, resolvê-lo de alguma forma.

Uma das reações a um gradiente desbotado (ou instável) é pensar se esse é realmente um problema sério. Vamos nos distrair brevemente do NS e imaginar que estamos tentando minimizar numericamente a função f (x) de uma variável. Não seria bom se a derivada f ′ (x) fosse pequena? Isso não significa que já estamos perto do extremo? E da mesma maneira, um pequeno gradiente nas primeiras camadas do GNS não significa que não precisamos mais ajustar muito pesos e deslocamentos?

Claro que não. Lembre-se de que inicializamos aleatoriamente os pesos e compensações da rede. É altamente improvável que nossos pesos e misturas originais funcionem bem com o que queremos de nossa rede. Como exemplo específico, considere a primeira camada de pesos na rede [784,30,30,30,10], que classifica os números MNIST. Inicialização aleatória significa que a primeira camada ejeta a maioria das informações sobre a imagem recebida. Mesmo que as camadas posteriores fossem cuidadosamente treinadas, seria extremamente difícil para elas determinar a mensagem recebida, simplesmente por falta de informações. Portanto, é absolutamente impossível imaginar que a primeira camada simplesmente não precise ser treinada. Se vamos treinar STS, precisamos entender como resolver o problema de um gradiente que desaparece.

O que causa o problema do gradiente de desbotamento? Gradientes instáveis ​​no GNS

Para entender como o problema de um gradiente de fuga aparece, considere o NS mais simples: com apenas um neurônio em cada camada. Aqui está uma rede com três camadas ocultas:



Aqui w ₁ , w ₂ , ... são pesos, b ₁ , b ₂ , ... são deslocamentos, C é uma determinada função de custo. Apenas para lembrá-lo, direi que a saída a _j do neurônio n. J é igual a σ (z _j ), onde σ é a função de ativação sigmóide usual e z _j = w _j a _{j - 1} + b _j é a entrada ponderada do neurônio. Descrevi a função de custo no final para enfatizar que o custo é uma função da saída da rede e ₄ : se a saída real estiver próxima do que você deseja, então o custo será pequeno e, se estiver longe, será grande.

Estudamos o gradiente ∂C / ∂b ₁ associado ao primeiro neurônio oculto. Encontramos a expressão para ∂C / ∂b ₁ e, depois de estudada, entenderemos por que o problema do gradiente de fuga surge.

Começamos demonstrando a expressão para ∂C / ∂b ₁ . Parece inexpugnável, mas, de fato, sua estrutura é simples, e eu a descreverei em breve. Aqui está esta expressão (por enquanto, ignore a própria rede e observe que σ é apenas uma derivada da função σ):



A estrutura da expressão é a seguinte: para cada neurônio na rede existe um termo de multiplicação σ ′ (z _j ), para cada peso existe w _j e também há o último termo, ∂C / ∂a ₄ , correspondente à função de custo. Observe que eu coloquei os membros correspondentes acima das partes correspondentes da rede. Portanto, a própria rede é uma regra mnemônica de expressão.

Você pode usar essa expressão com fé e pular sua discussão diretamente para o local em que é explicada como ela se relaciona com o problema do gradiente de desbotamento. Não há nada de errado nisso, pois essa expressão é um caso especial de nossa discussão sobre retropropagação. No entanto, é fácil explicar sua fidelidade, por isso será bastante interessante (e talvez instrutivo) para você estudar essa explicação.

Imagine que fizemos uma pequena alteração em Δb ₁ no deslocamento b ₁ . Isso enviará uma série de alterações em cascata pelo restante da rede. Primeiro, isso fará com que a saída do primeiro neurônio oculto Δa ₁ mude. Isso, por sua vez, força Δz ₂ a mudar a entrada ponderada para o segundo neurônio oculto. Então haverá uma mudança em Δa ₂ na saída do segundo neurônio oculto. E assim por diante, até uma alteração em ΔC no valor de saída. Acontece que:

$$

$$\ frac {\ parcial C} {\ parcial b_1} \ approx \ frac {\ Delta C} {\ Delta b_1} \ tag {114}$$

Isso sugere que podemos derivar uma expressão para o gradiente ∂C / ∂b ₁ , monitorando cuidadosamente a influência de cada etapa nessa cascata.

Para fazer isso, vamos pensar como Δb ₁ faz com que a saída _{1 do} primeiro neurônio oculto mude. Temos um ₁ = σ (z ₁ ) = σ (w ₁ a ₀ + b ₁ ), portanto

$$

$$\ Delta a_1 \ approx \ frac {\ parcial \ sigma (w_1 a_0 + b_1)} {\ parcial b_1} \ Delta b_1 \ tag {115}$$

$$

$$= \ sigma '(z_1) \ Delta b_1 \ tag {116}$$

O termo σ ′ (z ₁ ) deve parecer familiar: este é o primeiro termo de nossa expressão para o gradiente ∂C / ∂b ₁ . Intuitivamente, ele transforma a alteração no deslocamento Δb ₁ na mudança Δa _{1 da} ativação _da saída. A mudança em Δa _1, por sua vez, causa uma alteração na entrada ponderada z ₂ = w ₂ a ₁ + b _{2 do} segundo neurônio oculto:

$$

$$\ Delta z_2 \ approx \ frac {\ parcial z_2} {\ parcial a_1} \ Delta a_1 \ tag {117}$$

$$

$$= w_2 \ Delta a_1 \ tag {118}$$

Combinando as expressões para Δz ₂ e Δa ₁ , vemos como a mudança no viés b _{1 se} propaga ao longo da rede e afeta z ₂ :

$$

$$\ Delta z_2 \ approx \ sigma '(z_1) w_2 \ Delta b_1 \ tag {119}$$

E isso também deve ser familiar: estes são os dois primeiros termos em nossa expressão declarada para o gradiente ∂C / ∂b ₁ .

Isso pode ser continuado ainda mais, monitorando como as mudanças são propagadas pelo restante da rede. Em cada neurônio, selecionamos o termo σ ′ (z _j ) e, através de cada peso, selecionamos o termo w _j . Como resultado, é obtida uma expressão que relaciona a alteração final ΔC da função de custo com a alteração inicial Δb _{1 do} viés:

$$

$$\ Delta C \ approx \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ parcial C} {\ parcial a_4} \ Delta b_1 \ tag {120}$$

Dividindo por Δb ₁ , obtemos realmente a expressão desejada para o gradiente:

$$

$$\ frac {\ parcial C} {\ parcial b_1} = \ sigma '(z_1) w_2 \ sigma' (z_2) \ ldots \ sigma '(z_4) \ frac {\ parcial C} {\ parcial a_4} \ tag { 121}$$

Por que existe um problema de gradiente de desbotamento?

Para entender por que o problema do gradiente desaparece, vamos escrever em detalhes toda a nossa expressão para o gradiente:

$$

$$\ frac {\ parcial C} {\ parcial b_1} = \ sigma '(z_1) \ w_2 \ sigma' (z_2) \ w_3 \ sigma '(z_3) \, w_4 \ sigma' (z_4) \ \ frac {\ parcial C} {\ parcial a_4} \ tag {122}$$

Além do último termo, esta expressão é o produto de termos da forma w _j σ ′ (z _j ). Para entender como cada um deles se comporta, examinamos o gráfico da função σ:



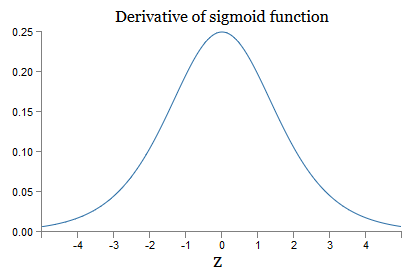
O gráfico atinge o máximo no ponto σ ′ (0) = 1/4. Se usarmos a abordagem padrão para inicializar os pesos da rede, selecionamos os pesos usando a distribuição Gaussiana, ou seja, a raiz quadrada média zero e o desvio padrão 1. Portanto, geralmente os pesos satisfazem a desigualdade | w _j | <1. Comparando todas essas observações, vemos que os termos w _j σ ′ (z _j ) geralmente satisfazem a desigualdade | w _j σ ′ (z _j ) | <1/4. E se pegarmos o produto do conjunto de tais termos, ele diminuirá exponencialmente: quanto mais termos, menor o produto. Começa a parecer uma possível solução para o problema do gradiente que desaparece.

Para escrever isso com mais precisão, comparamos a expressão para ∂C / ∂b ₁ com a expressão do gradiente em relação ao próximo deslocamento, por exemplo, ∂C / ∂b ₃ . Obviamente, não escrevemos uma expressão detalhada para ∂C / ∂b ₃ , mas segue as mesmas leis descritas acima para ∂C / ∂b ₁ . E aqui está uma comparação de duas expressões:



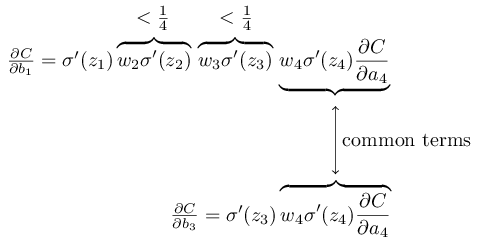
Eles têm vários membros em comum. No entanto, o gradiente ∂C / ∂b ₁ inclui dois termos adicionais, cada um dos quais tem a forma w _j σ ′ (z _j ). Como vimos, esses termos geralmente não excedem 1/4. Portanto, o gradiente ∂C / ∂b ₁ geralmente será 16 (ou mais) vezes menor que ∂C / ∂b ₃ . E esta é a principal causa do problema do gradiente que desaparece.

Obviamente, isso não é exato, mas é uma prova informal do problema. Existem várias advertências. Em particular, pode-se interessar se os pesos _wj aumentarão durante o treinamento. Se isso acontecer, os termos w _j σ ′ (z _j ) no produto não satisfarão mais a desigualdade | w _j σ ′ (z _j ) | <1/4. E se eles forem grandes o suficiente, mais de 1, não teremos mais o problema de um gradiente de desbotamento. Em vez disso, o gradiente aumentará exponencialmente à medida que você voltar pelas camadas. E, em vez do problema do gradiente desaparecer, temos o problema do crescimento explosivo do gradiente.

O problema do crescimento explosivo do gradiente

Vejamos um exemplo específico de um gradiente explosivo. O exemplo será um tanto artificial: ajustarei os parâmetros da rede para garantir a ocorrência de crescimento explosivo. Mas, embora o exemplo seja artificial, a vantagem é que ele demonstra claramente que o crescimento explosivo do gradiente não é uma possibilidade hipotética, mas pode realmente acontecer.

Para um crescimento gradiente explosivo, você precisa seguir duas etapas. Primeiro, escolhemos grandes pesos em toda a rede, por exemplo, w1 = w2 = w3 = w4 = 100. Então escolhemos essas mudanças para que os termos σ ′ (z _j ) não sejam muito pequenos. E isso é bastante fácil de fazer: precisamos apenas selecionar esses deslocamentos para que a entrada ponderada de cada neurônio seja zj = 0 (e então σ ′ (zj) = 1/4). Portanto, por exemplo, precisamos de z ₁ = w ₁ a ₀ + b ₁ = 0. Isso pode ser conseguido configurando b ₁ = −100 ∗ a ₀ . A mesma idéia pode ser usada para selecionar outros deslocamentos. Como resultado, veremos que todos os termos w _j σ ′ (z _j ) são iguais a 100 ∗ 14 = 25. E então obtemos um crescimento explosivo gradiente.

Problema instável do gradiente

O problema fundamental não é o problema do gradiente que desaparece ou o crescimento explosivo do gradiente. É que o gradiente nas primeiras camadas é o produto dos membros de todas as outras camadas. E quando há muitas camadas, a situação se torna essencialmente instável. E a única maneira que todas as camadas podem aprender com a mesma velocidade é escolher os membros do trabalho que se equilibrarão. E, na ausência de algum mecanismo ou razão para esse equilíbrio, é improvável que isso aconteça por acaso.Em suma, o verdadeiro problema é que o SN sofre do problema de um gradiente instável. E, no final, se usarmos técnicas de aprendizado padrão baseadas em gradiente, diferentes camadas da rede aprenderão em velocidades terrivelmente diferentes.

Exercício

• , |σ′(z)|<1/4. , , . ?

Vimos que o gradiente pode desaparecer ou crescer explosivamente nas primeiras camadas de uma rede profunda. De fato, ao usar neurônios sigmóides, o gradiente geralmente desaparece. Para entender o porquê, considere novamente a expressão | wσ ′ (z) |. Para evitar o problema do gradiente que desaparece, precisamos de | wσ ′ (z) | ≥1. Você pode decidir que isso é fácil de alcançar com valores muito grandes de w. No entanto, na realidade, não é tão simples. A razão é que o termo σ ′ (z) também depende de w: σ ′ (z) = σ ′ (wa + b), onde a é a ativação da entrada. E se fizermos w grande, precisamos tentar não fazer σ ′ (wa + b) pequeno em paralelo. E isso acaba sendo uma limitação séria. A razão é que, quando fazemos w grande, tornamos wa + b muito grande. Se você olhar para o gráfico de σ ′, pode-se ver que isso nos leva às “asas” da função σ ′,onde assume valores muito pequenos. E a única maneira de evitar isso é manter a ativação recebida em uma faixa de valores bastante estreita. Às vezes isso acontece por acidente. Mas mais frequentemente isso não acontece. Portanto, no caso geral, temos o problema de um gradiente de fuga.

• |wσ′(wa+b)|. , |wσ′(wa+b)|≥1. , , |w|≥4.
• , |w|≥4, , |wσ′(wa+b)|≥1.
• , , ,

  $$

  $$\frac{2}{|w|} \ln\left( \frac{|w|(1+\sqrt{1-4/|w|})}{2}-1\right) \tag{123}$$
• , |w|≈6.9, ≈0,45. , , , .
• . x, w ₁ , b w ₂ . , , , w ₂ σ(w ₁ x+b)≈x for x∈[0,1]. , , ( ). : x=1/2+Δ, , w ₁ , w ₁ Δ .

Estudamos redes de brinquedos com apenas um neurônio em cada camada oculta. E as redes profundas mais complexas que possuem muitos neurônios em cada camada oculta?



De fato, quase a mesma coisa acontece nessas redes. Anteriormente, no capítulo sobre propagação traseira, vimos que o gradiente na camada #l de uma rede com camadas L é especificado como:

$$

$$\delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}$$

Aqui Σ ′ (z ^l ) é a matriz diagonal, cujos elementos são os valores de σ ′ (z) para as entradas ponderadas da camada nº l. de w ^l - é a matriz de peso para diferentes camadas. E ∇ _a C é o vetor de derivadas parciais de C com relação às ativações de saída.

Essa expressão é muito mais complicada do que o caso de um neurônio. E, no entanto, se você olhar de perto, sua essência será muito semelhante, com um monte de pares da forma (w ^j ) ^T Σ ′ (z ^j ). Além disso, as matrizes Σ ′ (z ^j ) na diagonal têm valores pequenos, não mais que 1/4. Se as matrizes de peso w ^j não forem muito grandes, cada termo adicional (w ^j ) ^T Σ ′ (z ^l) tende a reduzir o vetor de gradiente, o que leva a um gradiente que desaparece. No caso geral, um número maior de termos de multiplicação leva a um gradiente instável, como no exemplo anterior. Na prática, empiricamente, geralmente em redes sigmóides, os gradientes nas primeiras camadas desaparecem exponencialmente rapidamente. Como resultado, o aprendizado nessas camadas diminui. E a desaceleração não é um acidente ou um inconveniente: é uma consequência fundamental da nossa abordagem escolhida para o aprendizado.

Outros obstáculos à aprendizagem profunda

Neste capítulo, concentrei-me nos gradientes desbotados - e mais geralmente no caso de gradientes instáveis ​​- como um obstáculo ao aprendizado profundo. De fato, gradientes instáveis ​​são apenas um obstáculo ao desenvolvimento da defesa civil, embora importante e fundamental. Uma parte significativa da pesquisa atual está tentando entender melhor os problemas que podem surgir no ensino de GO. Não descreverei todos esses trabalhos em detalhes, mas quero mencionar brevemente alguns trabalhos para dar uma idéia de algumas perguntas feitas por pessoas.

Como primeiro exemplo em 2010foram encontradas evidências de que o uso das funções de ativação sigmóide pode levar a problemas no aprendizado da SN. Em particular, foram encontradas evidências de que o uso de um sigmóide levará ao fato de que as ativações da última camada oculta durante o treinamento serão saturadas na região 0, o que diminuirá seriamente o treinamento. Várias funções alternativas de ativação foram propostas que não sofrem tanto com o problema de saturação (consulte também outro documento de discussão ).

Como primeiro exemplo, em 2013, o efeito da inicialização aleatória dos pesos e do gráfico de pulsos em uma descida estocástica do gradiente com base em um pulso foi estudado no GO. Nos dois casos, uma boa escolha influenciou significativamente a capacidade de treinar STS.

Esses exemplos sugerem que a pergunta "Por que o STS é tão difícil de treinar?" muito complicado Neste capítulo, focamos nas instabilidades associadas ao treinamento em gradiente do GNS. Os resultados dos dois parágrafos anteriores indicam que a escolha da função de ativação, o método de inicialização dos pesos e até os detalhes da implementação do treinamento baseado na descida do gradiente também desempenham um papel. E, é claro, a escolha da arquitetura de rede e outros hiperparâmetros será importante. Portanto, muitos fatores podem desempenhar um papel na dificuldade de aprender redes profundas, e a questão de entender esses fatores é objeto de pesquisas em andamento. Mas tudo isso parece sombrio e inspira pessimismo. No entanto, há boas notícias - no próximo capítulo, tudo será a nosso favor e desenvolveremos várias abordagens no GO,que até certo ponto serão capazes de superar ou contornar todos esses problemas.